Symetralne boków trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu opisanego na tym trójkącie.

Środek okręgu opisanego na trójkącie:

• ostrokątnym leży wewnątrz trójkąta;

• prostokątnym leży na środku przeciwprostokątnej;

• rozwartokątnym leży na zewnątrz trójkąta.

Trójkąt $ABC$ jest trójkątem równoramiennym. Punkt $O$ jest środkiem okręgu opisanego na tym trójkącie, zaś $D$ – spodkiem wysokości opuszczonej z wierzchołka $C$ na podstawę $AB$. Obliczymy długość promienia tego okręgu, jeśli:

a) $\left|CD\right|=5$ i $\left|AB\right|=4$,

b) $\left|CD\right|=3$ i $\left|AB\right|=8$.

Rozwiązanie

a) Skoro $\left|CD\right|=5$ i $\left|AB\right|=4$, to trójkąt $ABC$ jest trójkątem ostrokątnym:

RD4sbZEnwnnh7

Ilustracja przedstawia trójkąt A B C, który jest wpisany w okrąg. Z wierzchołka C linią przerywaną poprowadzono wysokość, spodek wysokości podpisano literą D. Odcinek AD oraz BD ma długość 2. Środek okręgu podpisano literą O, leży on na wysokości CD. Odcinek AO podpisano literą R.

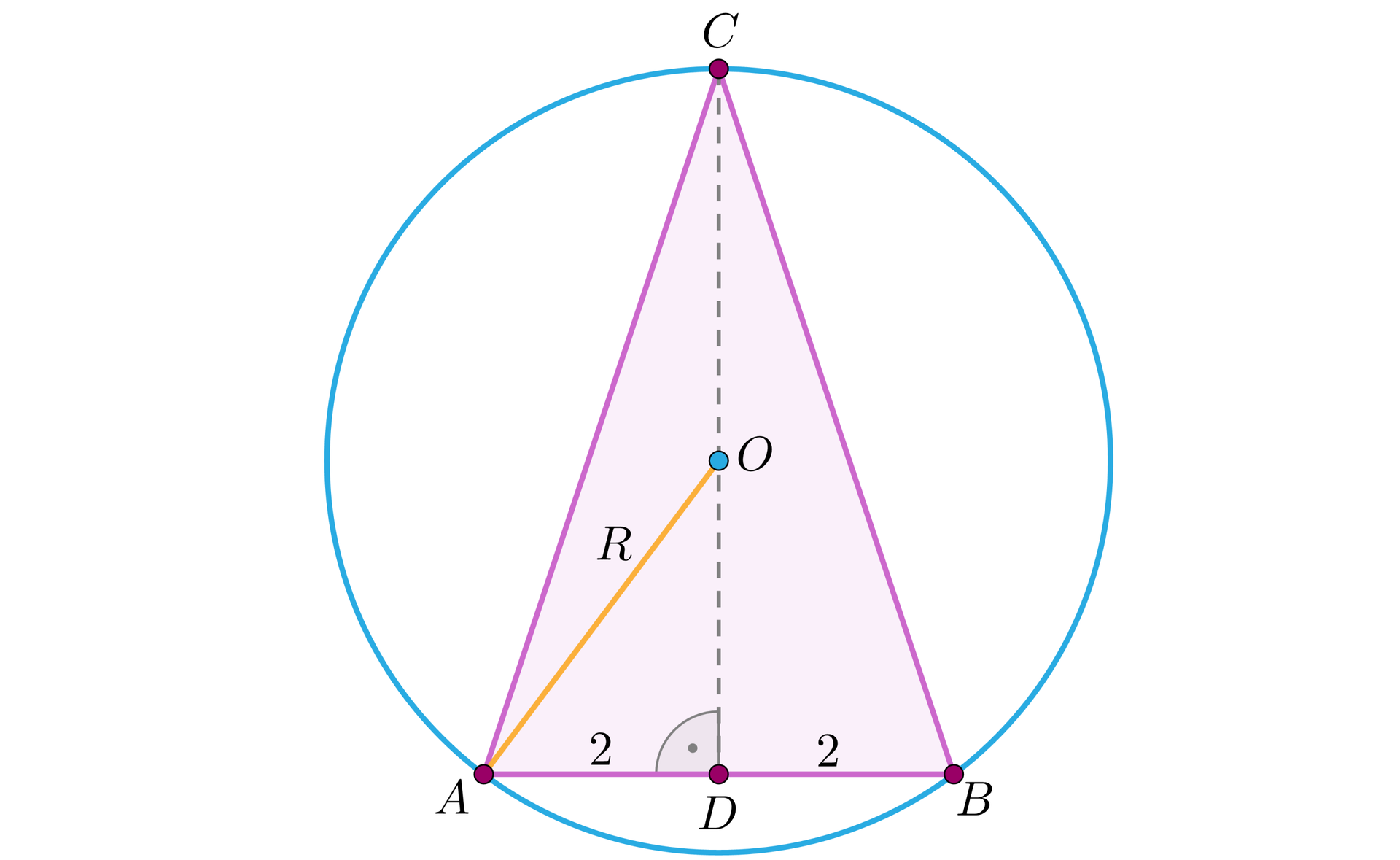
Zwróćmy uwagę, że $\left|OD\right|=\left|CD\right|-\left|CO\right|=5-R$

Stosując twierdzenie Pitagorasa dla trójkąta prostokątnego $ADO$, otrzymujemy:

$R^2={\left(5-R\right)}^2+2^2$

$R^2=25-10R+R^2+4$

$10R=29$

$R=2,9$

b) Skoro $\left|CD\right|=3$ i $\left|AB\right|=8$, to trójkąt $ABC$ jest trójkątem rozwartokątnym:

RHyoH4e4GQjKW

Ilustracja przedstawia trójkąt A B C, który jest wpisany w okrąg. Z wierzchołka C linią przerywaną poprowadzono wysokość, spodek wysokości podpisano literą D. Odcinek AD oraz BD ma długość 4. Środek okręgu podpisano literą O, leży on poza trójkątem. Odcinek AO podpisano literą R.

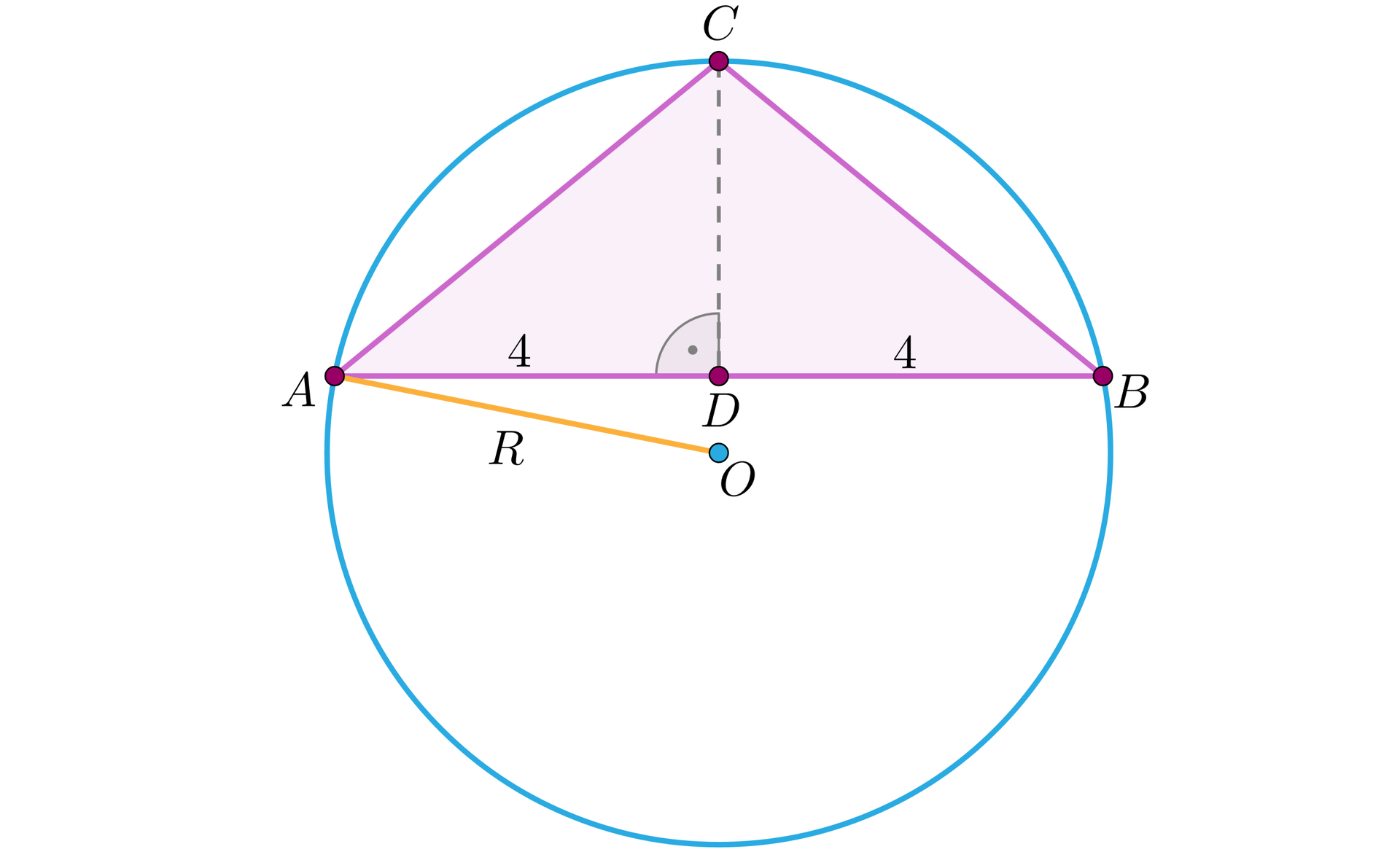
Z ilustracji graficznej widzimy, że $\left|OC\right|=R$, zaś $\left|OD\right|=R-3$.

Stosując twierdzenie Pitagorasa do trójkąta prostokątnego $ADO$ otrzymujemy:

$R^2={\left(R-3\right)}^2+4^2$

$R^2=R^2-6R+9+16$

$6R=25$

$R=4\frac{1}{6}$

Obliczymy długość promienia okręgu opisanego na trójkącie prostokątnym:

a) równoramiennym o przyprostokątnej długości $6 \mathrm{cm}$,

b) o przyprostokątnych długości $15 \mathrm{cm}$ i $8 \mathrm{cm}$.

Rozwiązanie

a) Skoro mamy trójkąt prostokątny, to wiemy już, że środek okręgu opisanego na trójkącieokrąg opisany na trójkącieokręgu opisanego na trójkącie prostokątnym leży na środku przeciwprostokątnej, zatem długość promienia tego okręgu równa jest połowie długości przeciwprostokątnej.

$R=\frac{1}{2}c$, gdzie $c$ jest długością przeciwprostokątnej.

Na początek przypomnijmy sobie zależności, jakie są charakterystyczne dla trójkąta prostokątnego równoramiennego.

RbIehrkwMkYur

Ilustracja przedstawia trójkąt prostokątny A B C, który jest wpisany w okrąg. Odcinki AC i BC mają długość a, przeciwprostokątna AB ma długość $a\sqrt{2}$. Na odcinku AB leży punkt O będący środkiem okręgu.

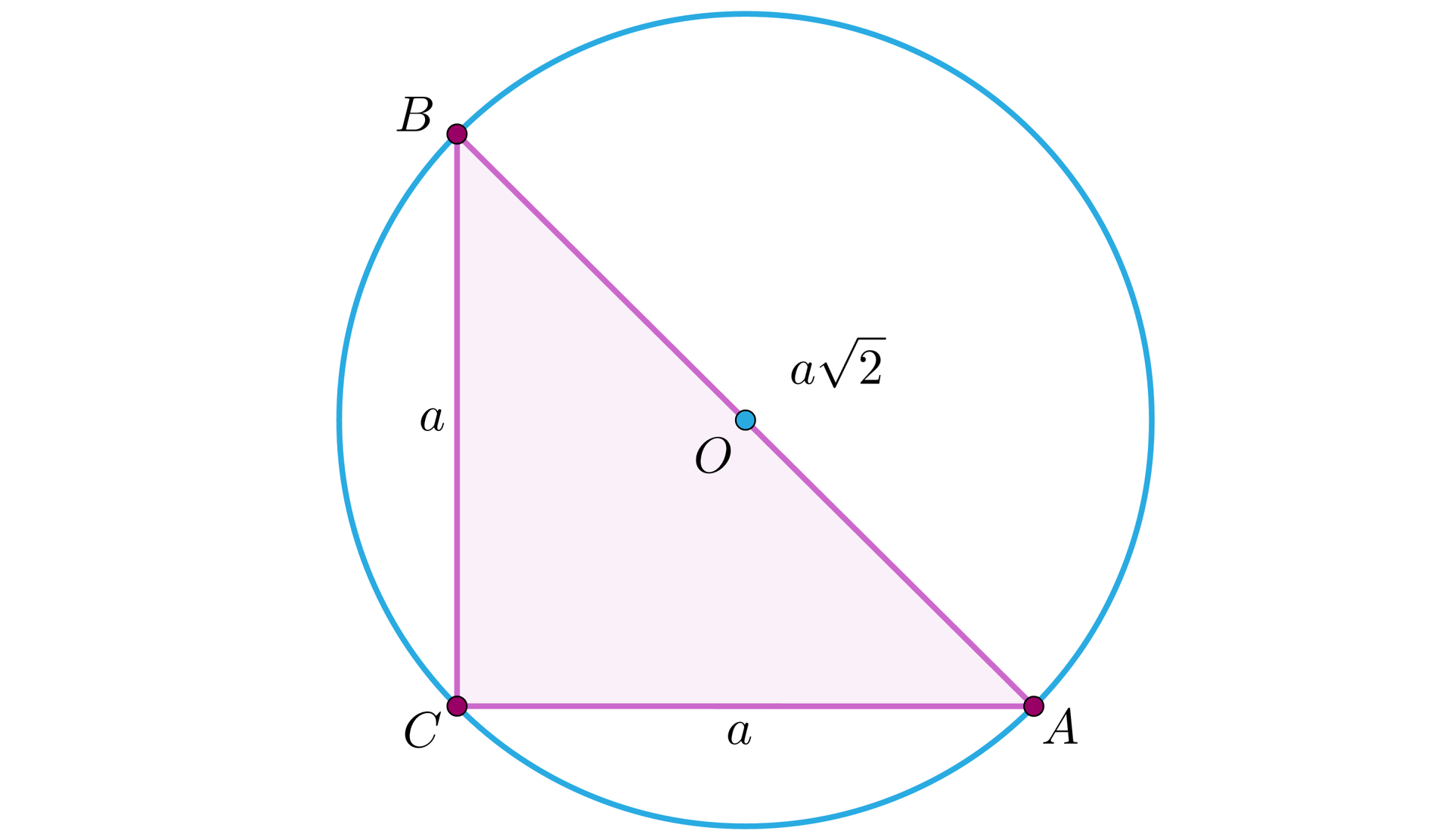
Nasze przyprostokątne są długości $6 \mathrm{cm}$, zatem przeciwprostokątna jest długości $6\sqrt{2} \mathrm{cm}$.

$R=\frac{1}{2}·6\sqrt{2}=3\sqrt{2} \left[\mathrm{cm}\right]$

b) Wiemy, że potrzebujemy długości przeciwprostokątnej, zatem stosujemy twierdzenie Pitagorasa, by ją obliczyć.

Załóżmy, że nasza przeciwprostokątna, to $c$, wówczas otrzymujemy:

$c^2={15}^2+8^2$

$c^2=225+64$

$c^2=289$

$c=17 \left[\mathrm{cm}\right]$

Znając długość przeciwprostokątnej, obliczymy długość promienia okręgu opisanego na tym trójkącie

$R=\frac{1}{2}·17=8,5 \left[\mathrm{cm}\right]$.

W trójkącie równobocznym symetralnesymetralnasymetralne zawierają wysokości tego trójkąta, które przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku $2:1$, licząc od wierzchołka.

Obliczymy długość promienia koła opisanego na trójkącie równobocznym o polu $36\sqrt{3}$.

Rozwiązanie

Na początek korzystając ze wzoru na pole trójkąta równobocznego $P=\frac{a^2\sqrt{3}}{4}$ obliczymy długość boku trójkąta.

$36\sqrt{3}=\frac{a^2\sqrt{3}}{4}$

$a^2=144$

$a=12$

Mając długość boku, bez problemu obliczymy $R$.

$R=\frac{12\sqrt{3}}{3}=4\sqrt{3}$

Wyznaczymy miarę kąta $\alpha$ z rysunku.

R1OhGZdPb4JlY

Ilustracja przedstawia trójkąt wpisany w okrąg. Jeden z kątów trójkąta podpisano literą alfa. Z pozostałych dwóch kątów poprowadzono odcinki do środka okręgu, odcinki te podpisano literą r. Pomiędzy bokiem trójkąta a odcinkiem wychodzącym z tego samego wierzchołka do środka okręgu ma miarę 25 stopni.

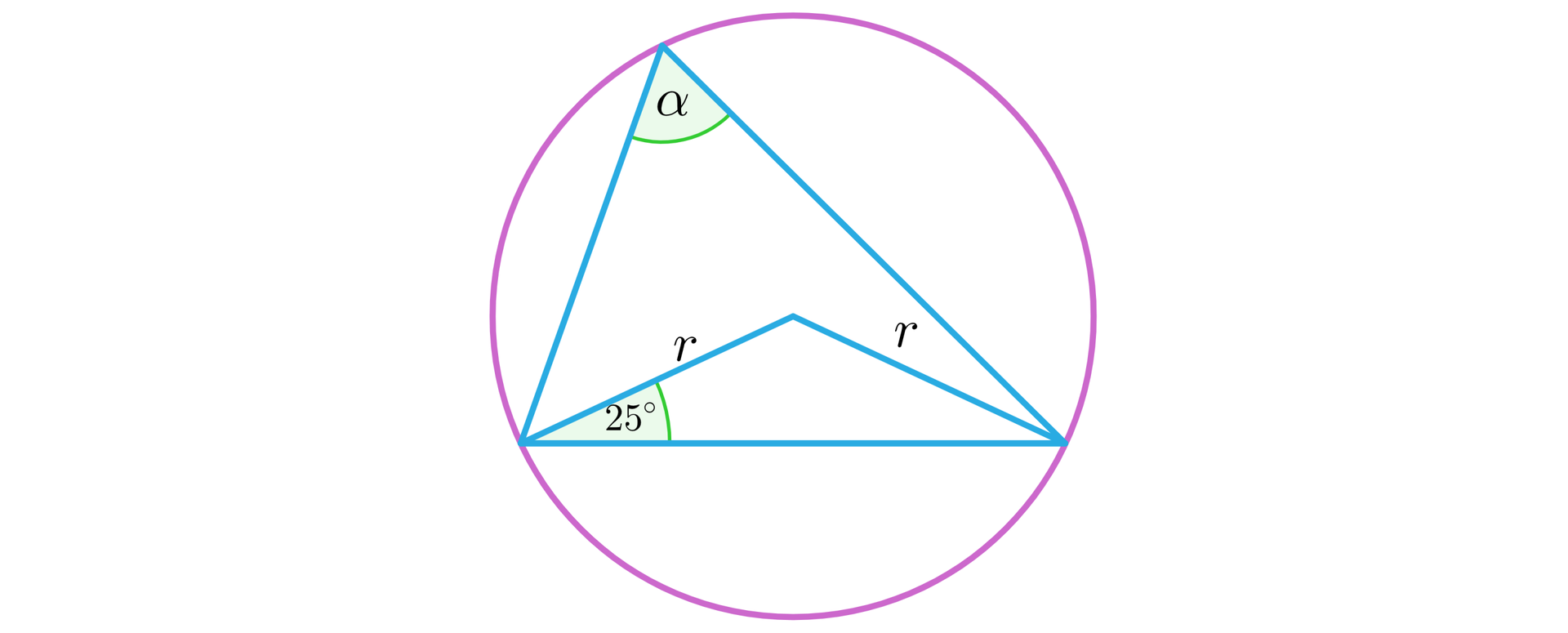
Rozwiązanie

Wprowadźmy dodatkowe oznaczenia na rysunku.

R1BxuLLpZtKND

Ilustracja przedstawia trójkąt wpisany w okrąg. Jeden z kątów trójkąta podpisano literą alfa. Z pozostałych dwóch kątów poprowadzono odcinki do środka okręgu, odcinki te podpisano literą r. Pomiędzy bokiem trójkąta a odcinkiem wychodzącym z tego samego wierzchołka do środka okręgu ma miarę 25 stopni. Kąt pomiędzy odcinkami o długości r podpisano literą beta.

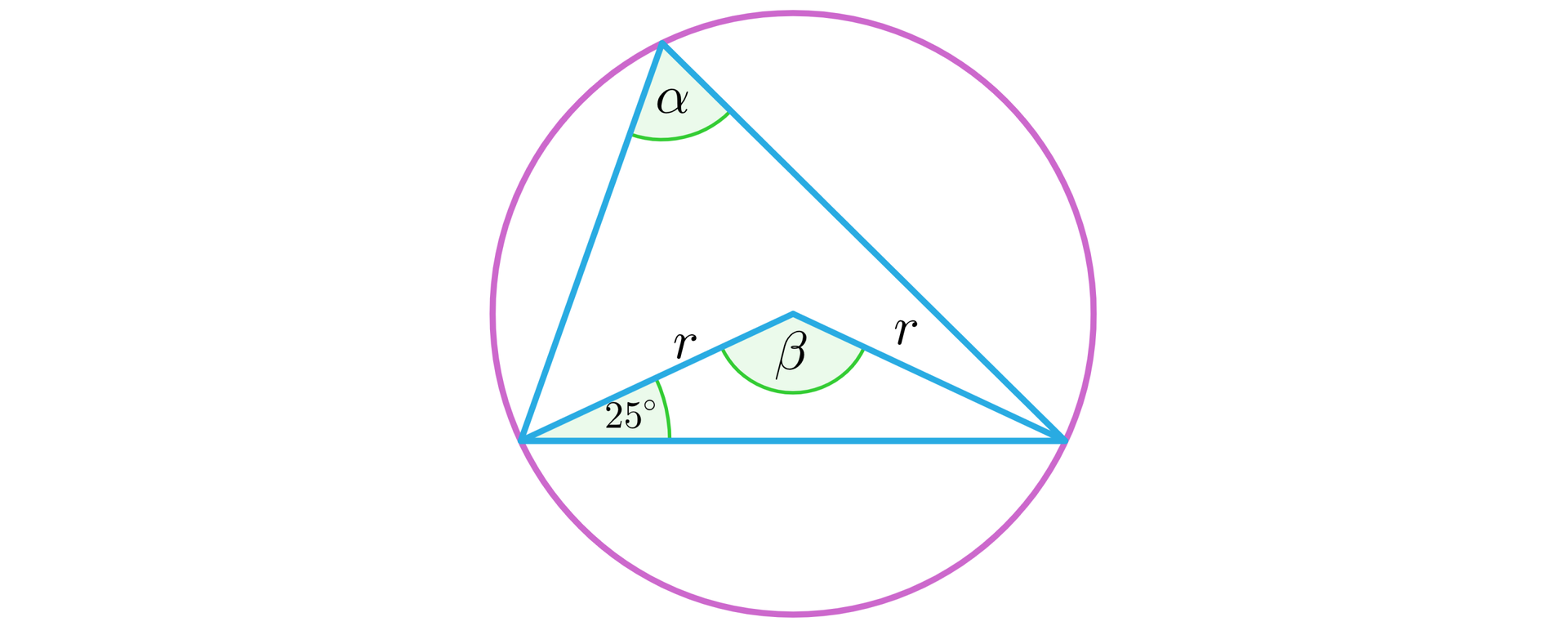
Zauważmy, że trójkąt o kątach $25°,\beta$ oraz bokach długości $r$ jest równoramienny, zatem:

$\beta =180°-2·25°=130°$

Ponieważ $\alpha$ jest kątem wpisanym, a $\beta$ kątem środkowym opartym na tym samym łuku co kąt $\alpha$, to z własności kątów wpisanych i środkowych w kolewłasności kątów wpisanych i środkowych w kolewłasności kątów wpisanych i środkowych w kole mamy

$\beta =2\alpha$, czyli $\alpha =\frac{1}{2}\beta$

Zatem $\alpha =\frac{1}{2}·130°=65°$.

Punkt $O$ jest środkiem okręgu opisanego na trójkącie ostrokątnym $ABC$. Kąt $ACO$ jest cztery razy większy od kąta $BAO$, a miara kąta $CBO$ jest o $12°$ większa od miary kąta $ABO$. Obliczymy miary kątów trójkąta $ABC$.

Rozwiązanie

Narysujmy okrąg o środku w punkcie $O$ opisany na trójkącie $ABC$ i wprowadźmy oznaczenia, jak na rysunku.

RurpYUa52k6Yt

Ilustracja przedstawia trójkąt A b C wpisany w okrąg, środek okręgu podpisano literą O. Z każdego z wierzchołków poprowadzono odcinek do punktu O.

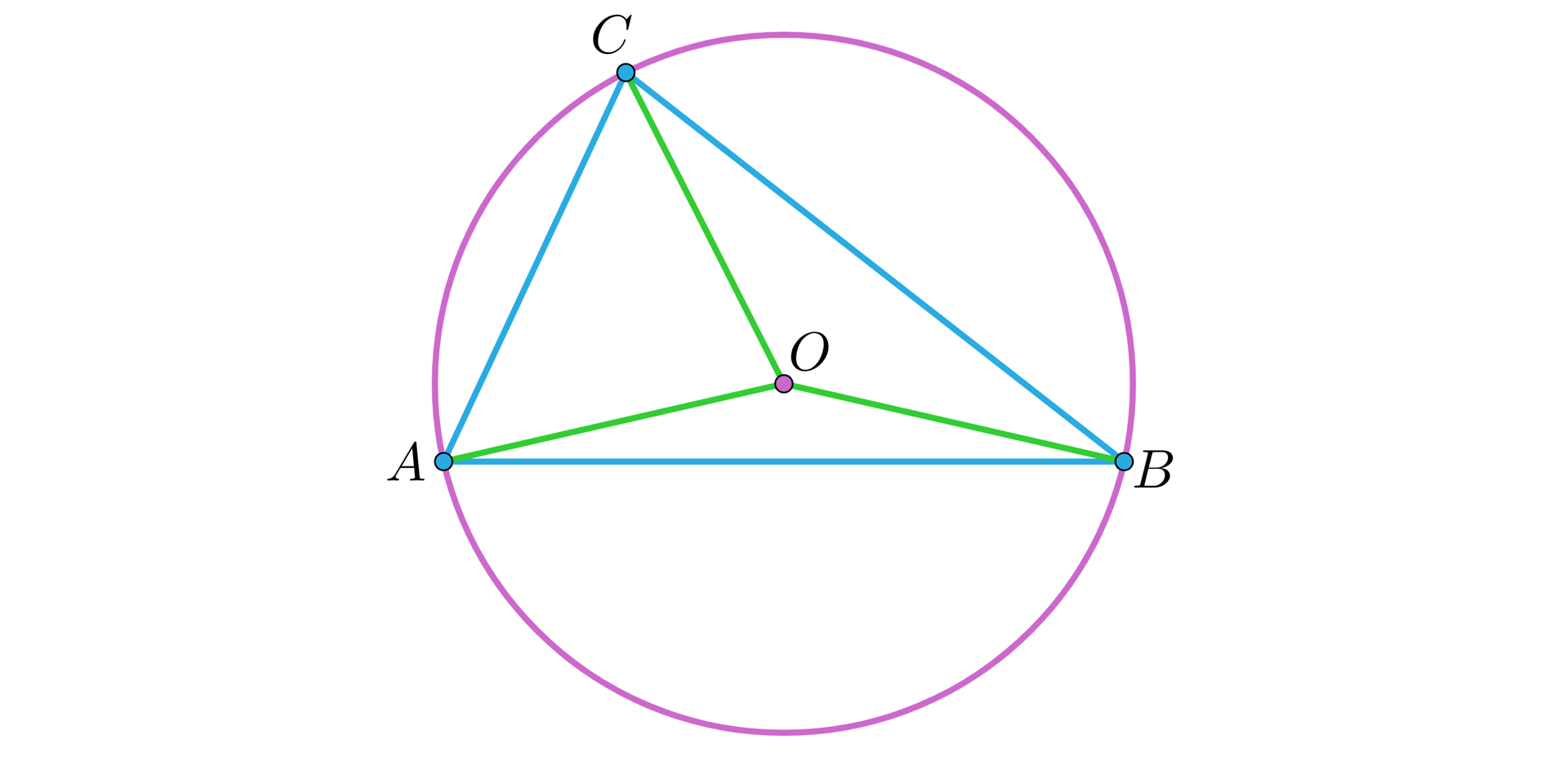
Niech $\left|\sphericalangle BAO\right|=\alpha$.

Wobec tego $\left|\sphericalangle ACO\right|=4\alpha$.

Zauważmy, że trójkąty $ABO$, $BCO$ oraz $ACO$ są równoramienne.

Zatem:

$\left|\sphericalangle ACO\right|=\left|\sphericalangle CAO\right|=4\alpha$

$\left|\sphericalangle BAO\right|=\left|\sphericalangle ABO\right|=\alpha$

$\left|\sphericalangle BCO\right|=\left|\sphericalangle CBO\right|=\alpha +12°$

Wobec faktu, że suma miar kątów wewnętrznych w trójkącie wynosi $180°$, by wyznaczyć wartość $\alpha$, rozwiązujemy równanie:

$4\alpha +4\alpha +\alpha +\alpha +\alpha +12°+\alpha +12°=180°$

$12\alpha =156°$

$\alpha =13°$

Zatem miary kątów trójkąta $ABC$ wynoszą:

$\left|\sphericalangle BAC\right|=13°+52°=65°$

$\left|\sphericalangle ACB\right|=52°+25°=77°$

$\left|\sphericalangle ABC\right|=13°+25°=38°$

Pokażemy, że odległość wierzchołka trójkąta $ABC$ od ortocentrumortocentrumortocentrum jest dwa razy dłuższa od odległości środka okręgu opisanego na trójkącie $ABC$ od środka przeciwległego boku.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku:

R1DL71ATlUJlA

Ilustracja przedstawia okrąg A b C, który jest wpisany w trójkąt. Przez wierzchołek A oraz B poprowadzono proste, w których zawierają się wysokości. Punkt przecięcia się tych prostych zaznaczono literą O. W trójkącie dla boku BC i AC poprowadzono proste zawierające symetralne, punkt przecięcia się symetralnych podpisano literą S. Punkt przecięcia się symetralnej boku AC z tym bokiem podpisano literą M. Punkt przecięcia się symetralnej boku BC z tym bokiem podpisano literą K. Na boku AB zaznaczono punkt N. W trójkącie A B C zaznaczono trójkąt A O C oraz trójkąt K S N.

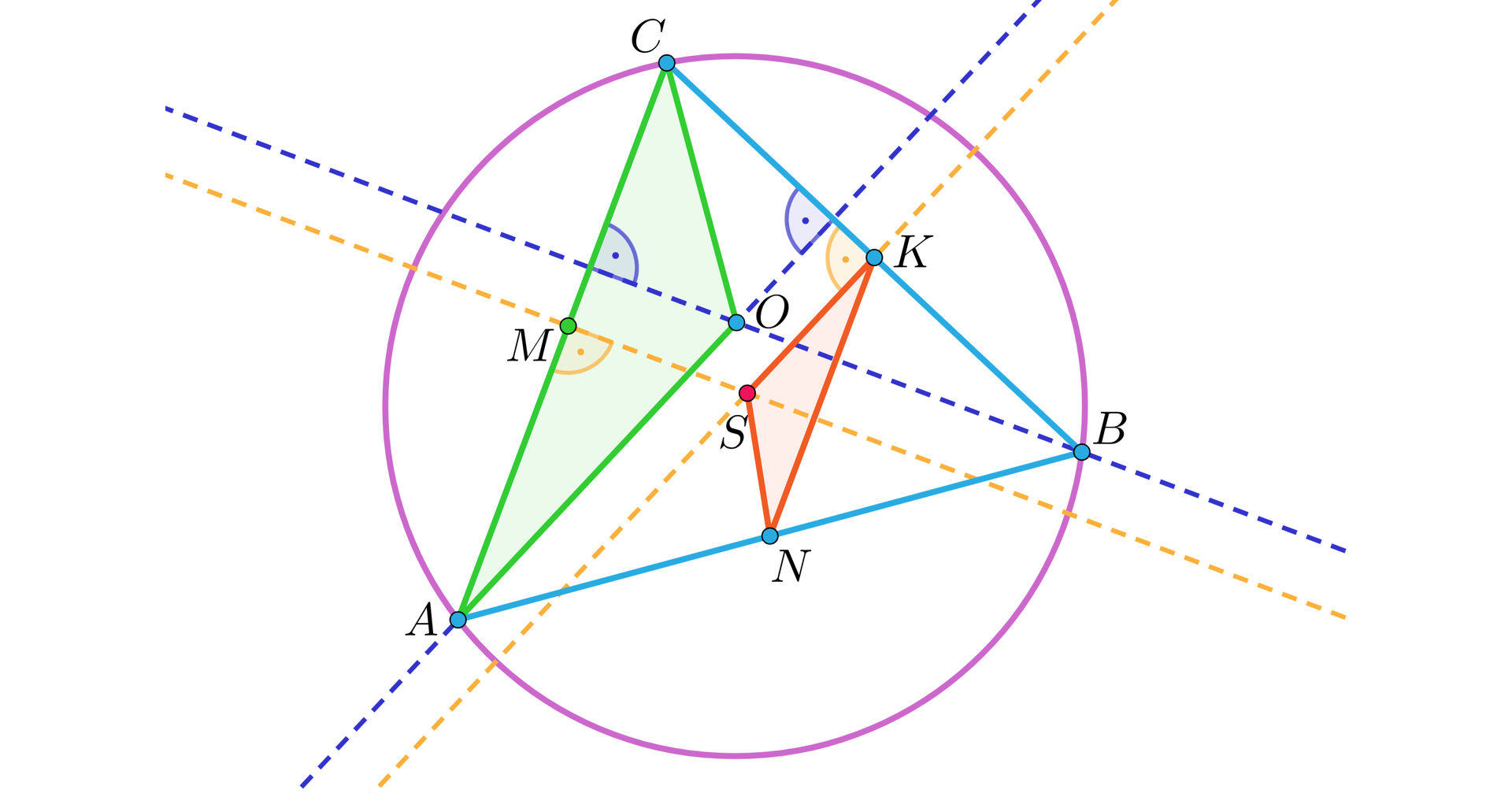
gdzie $O$ oznacza ortocentrum trójkąta $ABC$, zaś $S$ – środek okręgu opisanego na trójkącie $ABC$.

Zauważmy, że trójkąty $ACO$ i $KNS$ są podobne, gdyż $AO\parallel SK$, $CO\parallel SN$ oraz $AC\parallel KN$ , co oznacza, że: $\left|\sphericalangle COA\right|=\left|\sphericalangle KSN\right|$, $\left|\sphericalangle ACO\right|=\left|\sphericalangle KNS\right|$ i $\left|\sphericalangle OAC\right|=\left|\sphericalangle SKN\right|$. Ponieważ odcinek $KN$ jest odcinkiem środkowym trójkąta $ABC$, to skala tego podobieństwa wynosi $\frac{1}{2}$.

To oznacza, że: $\left|SK\right|=\frac{1}{2}\left|AO\right|$ co należało udowodnić.

symetralna boku to prosta prostopadła do tego boku, przechodząca przez jego środek; istotną własnością symetralnej jest fakt, że punkt leżący na niej jest równooddalony od końców tego odcinka

okrąg jest opisany na trójkącie, jeżeli wszystkie wierzchołki trójkąta leżą na okręgu; wówczas powiemy, że trójkąt jest wpisany w okrąg

punkt przecięcia wysokości trójkąta

1. miara kąta środkowego jest dwa razy większa niż miara kąta wpisanego opartego na tym samym łuku

2. miary kątów wpisanych opartych na tym samym łuku są równe