Przeczytaj

Już wiesz

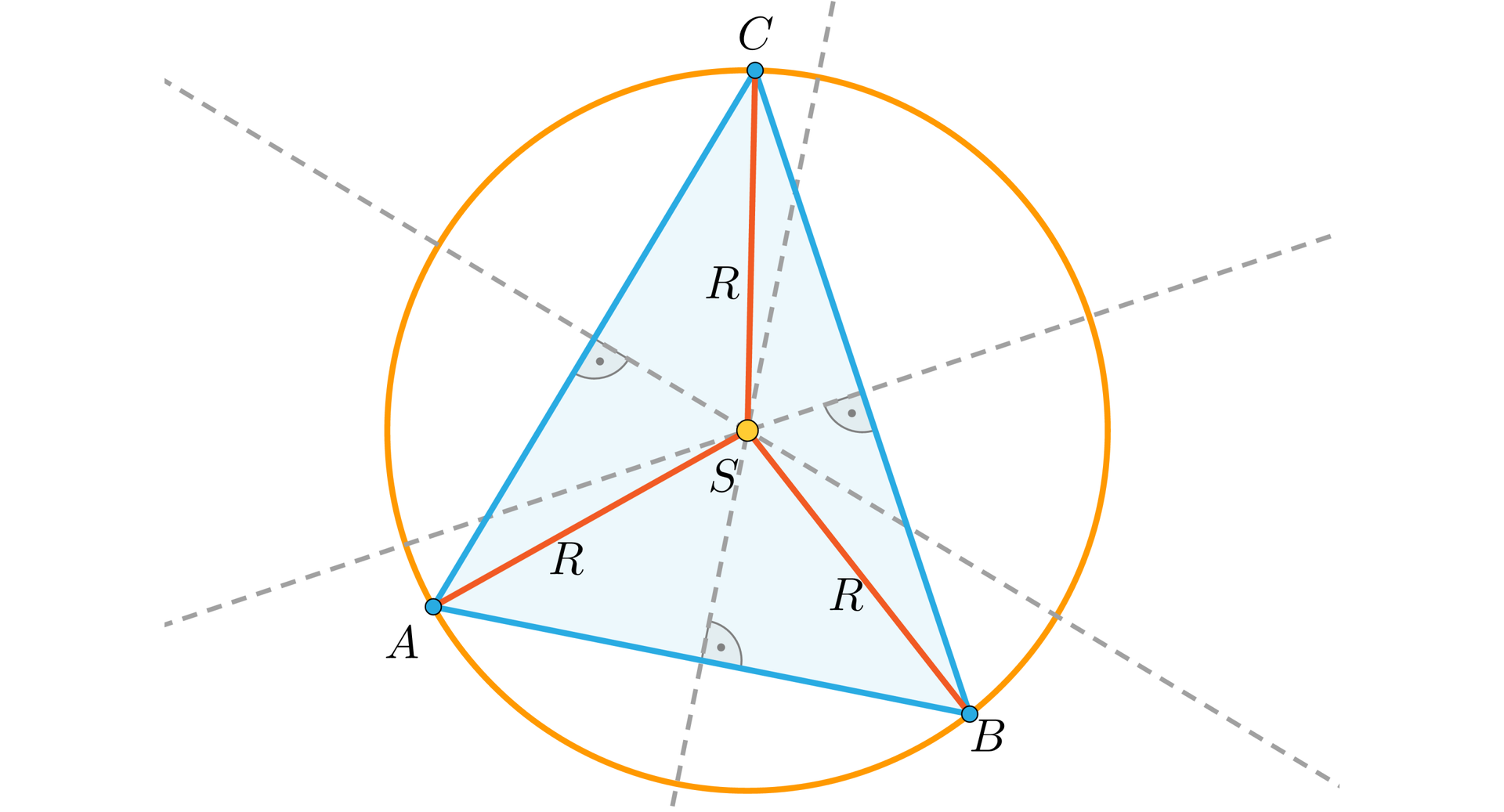
Symetralnesymetralna boku trójkątaSymetralne trzech boków trójkąta przecinają się w jednym punkcie. Punkt przecięcia $S$ leży w równej odległości od wierzchołków trójkąta $A$ , $B$ , $C$ , zatem przez te wierzchołki można poprowadzić okrąg o środku $S$ i promieniu $R$ .

Okrąg, który przechodzi przez wszystkie wierzchołki trójkąta, nazywamy okręgiem opisanym na trójkącie, a o trójkącie powiemy, że jest to trójkąt wpisany w okrąg. Z powyższego wynika, że na każdym trójkącie można opisać okrąg.

R1c0Gm7C6zn7M

Na ilustracji przedstawiono okrąg o środku w punkcie S. Punkt S stanowi środek przecięcia symetralnych boków AB, BC, AC. W okrąg wpisano trójkąt ABC. Zaznaczono promień R, łączący wierzchołki A, C, B ze środkiem okręgu S.

Przypomnimy teraz równanie okręgu. Można je zapisać w postaci kanonicznej:

{(x - a)}^{2} + {(y - b)}^{2} = r^{2}

gdzie punkt o współrzędnych $(a, b)$ jest środkiem okręgu, zaś $r$ jest długością jego promienia.

Równanie to możemy zapisać również w postaci ogólnej:

x^{2} + y^{2} - 2 a x - 2 b y + c = 0

Równanie to jest równaniem okręgu wtedy i tylko wtedy, gdy:

a^{2} + b^{2} - c > 0

Środek okręgu $C$ i jego promień $r$ wyznaczamy ze wzorów:

S = (a, b)

r = \sqrt{a^{2} + b^{2} - c}

Przykład 1

Wyznaczymy równanie okręgu opisanego na trójkącie o wierzchołkach $A = (2, 1)$ , $B = (- 3, 0)$ , $C = (1, 4)$ .

Rozwiązanie:

Sposób $I$ : metoda analityczna

R1OiKvZJJYy2H

Na ilustracji przedstawiono poziomą oś x od minus pięciu do pięciu, oraz pionową oś y od minus jeden do pięciu. Na płaszczyźnie narysowano trójkąt o wierzchołku A w punkcie 2;1, wierzchołku B w punkcie -3;0, wierzchołku C w punkcie 1;4. Na trójkącie ABC opisano okrąg.

Skorzystamy z równania $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , w którym niewiadomymi są $a$ , $b$ , $c$ .

Rozwiążemy układ równań:

$\{\begin{cases} 4 + 1 - 4 a - 2 b + c = 0 (1) \\ 9 + 6 a + c = 0 (2) \\ 1 + 16 - 2 a - 8 a + c = 0 (3) \end{cases}$

Wyznaczamy $c$ z równania $(2)$ :

$c = - 9 - 6 a$

Równania $(1)$ i $(3)$ odejmujemy stronami:

$5 - 4 a - 2 b + c - 17 + 2 a + 8 b - c = 0$ .

Mamy zatem:

$6 b = 2 a + 12$ ,

czyli:

$b = \frac{1}{3} a + 2$

Z równania $(3)$ :

$17 - 2 a - 8 (\frac{1}{3} a + 2) - 9 - 6 a = 0$

$- \frac{32}{3} a - 8 = 0$

Stąd: $a = - \frac{3}{4}$ ; $b = \frac{7}{4}$ ; $c = - \frac{9}{2}$ .

Równanie okręgu ma zatem postać:

$x^{2} + y^{2} + \frac{3}{2} x - \frac{7}{2} y - \frac{9}{2} = 0$ .

Sposób $II$ : metoda analityczna z rozważaniami geometrycznymi

RogPUpzzciZl8

Wyznaczymy punkt przecięcia $D$ symetralnych boków $A B$ i $B C$ . Obliczmy współczynnik kierunkowy oraz współrzędne punktu $M$ , który jest środkiem odcinka $A B$ .

$a_{A B} = \frac{0 - 1}{- 3 - 2} = \frac{- 1}{- 5} = \frac{1}{5}$ ,

$M = (\frac{2 + (- 3)}{2}, \frac{1 + 0}{2}) = (- \frac{1}{2}, \frac{1}{2})$ .

Symetralna boku $A B$ jest do tego boku prostopadła, ma więc współczynnik kierunkowy równy $- 5$ . Równaniem tej symetralnej jest zatem równanie:

$y - \frac{1}{2} = - 5 (x + \frac{1}{2})$ ,

a po przekształceniu:

$y = - 5 x - 2$ .

Wyznaczymy analogicznie równanie symetralnej boku $B C$ i współrzędne punktu $N$ :

$a_{B C} = \frac{4 - 0}{1 - (- 3)} = 1$ ,

$N = (- 1, 2)$ .

Symetralna boku $B C$ ma współczynnik kierunkowy $- 1$ , zatem jej równanie ma postać:

$y - 2 = - (x + 1)$ ,

czyli

$y = - x + 1$ .

Współrzędne punktu $D$ otrzymamy, rozwiązując układ równań:

$\{\begin{cases} y = - 5 x - 2 \\ y = - x + 1 \end{cases}$

Środek $D$ ma zatem współrzędne: $D = (- \frac{3}{4}, \frac{7}{4})$ .

Pozostaje nam obliczenie długości promienia.

$r = |D B| = \sqrt{{(- 3 + \frac{3}{4})}^{2} + {(\frac{7}{4})}^{2}} = \sqrt{\frac{130}{16}}$ .

Równanie okręgu opisanego na trójkącie $A B C$ ma zatem postać:

${(x + \frac{3}{4})}^{2} + {(y - \frac{7}{4})}^{2} = \frac{130}{16}$

co, po przekształceniu do postaci ogólnej, daje:

$x^{2} + y^{2} + \frac{3}{2} x - \frac{7}{2} y - \frac{9}{2} = 0$ .

Jak widać, sposób II jest bardziej czasochłonny. Powstaje zatem pytanie: Czy nie ma gotowych wzorów, z których moglibyśmy obliczyć współczynniki $a$ , $b$ , $c$ równania okręgu, na którym leżą punkty $(x_{1}, y_{1})$ , $(x_{2}, y_{2})$ , $(x_{3}, y_{3})$ ?

Takie wzory są:

$a = \frac{- {x_{1}}^{2} y_{2} + {x_{1}}^{2} y_{3} + {x_{2}}^{2} y_{1} - {x_{2}}^{2} y_{3} - {x_{3}}^{2} y_{1} + {x_{3}}^{2} y_{2} - {y_{1}}^{2} y_{2} + {y_{1}}^{2} y_{3} + {y_{1} y_{2}}^{2} - {y_{1} y_{3}}^{2} - {y_{2}}^{2} y_{3} + {y_{2} y_{3}}^{2}}{x_{1} y_{2} - x_{1} y_{3} - x_{2} y_{1} + x_{2} y_{3} + x_{3} y_{1} - x_{3} y_{2}}$

$b = \frac{{x_{1}}^{2} x_{2} - {x_{1}}^{2} x_{3} - {x_{1} x_{2}}^{2} + - {x_{1} x_{3}}^{2} - x_{1} {y_{2}}^{2} + x_{1} {y_{3}}^{2} + {x_{2}}^{2} x_{3} - x_{2} {x_{3}}^{2} + x_{2} {y_{1}}^{2} - x_{2} {y_{3}}^{2} - x_{3} {y_{1}}^{2} + x_{3} {y_{2}}^{2}}{x_{1} y_{2} - x_{1} y_{3} - x_{2} y_{1} + x_{2} y_{3} + x_{3} y_{1} - x_{3} y_{2}}$

$c = \frac{- {x_{1}}^{2} x_{2} y_{3} + {x_{1}}^{2} x_{3} y_{2} + x_{1} {x_{2}}^{2} y_{3} - x_{1} {x_{3}}^{2} y_{2} + x_{1} y {_{2}}^{2} y_{3} {- x_{1}}^{2} y_{2} y_{3} - {x_{2}}^{2} x_{3} y_{1} + x_{2} {x_{3}}^{2} y_{1} - x_{2} {y_{1}}^{2} y_{3}}{x_{1} y_{2} - x_{1} y_{3} - x_{2} y_{1} + x_{2} y_{3} + x_{3} y_{1} - x_{3} y_{2}} +$

$+ \frac{x_{2} y_{1} {y_{3}}^{2} + x_{3} {y_{1}}^{2} y_{2} - x_{3} y_{1} {y_{2}}^{2}}{x_{1} y_{2} - x_{1} y_{3} - x_{2} y_{1} + x_{2} y_{3} + x_{3} y_{1} - x_{3} y_{2}}$

jednak korzystanie z nich może powodować liczne błędy rachunkowe.

Przykład 2

Wykażemy analitycznie, że jeśli punkt $P$ jest wierzchołkiem trójkąta prostokątnego o przeciwprostokątnej $A B$ , to $P$ leży na okręgu, którego środkiem jest środek przeciwprostokątnej $A B$ a promień ma długość połowy długości $|A B|$ .

Rozwiązanie:

Wybierzmy dogodnie układ współrzędnych, tzn. tak, że:

odcinek $A B$ leży na osi $X$ , a jego końce są symetryczne względem początku układu $O$ ;
oś $Y$ jest osią symetrii odcinka $A B$ .

R1KJOXL1PBD6L

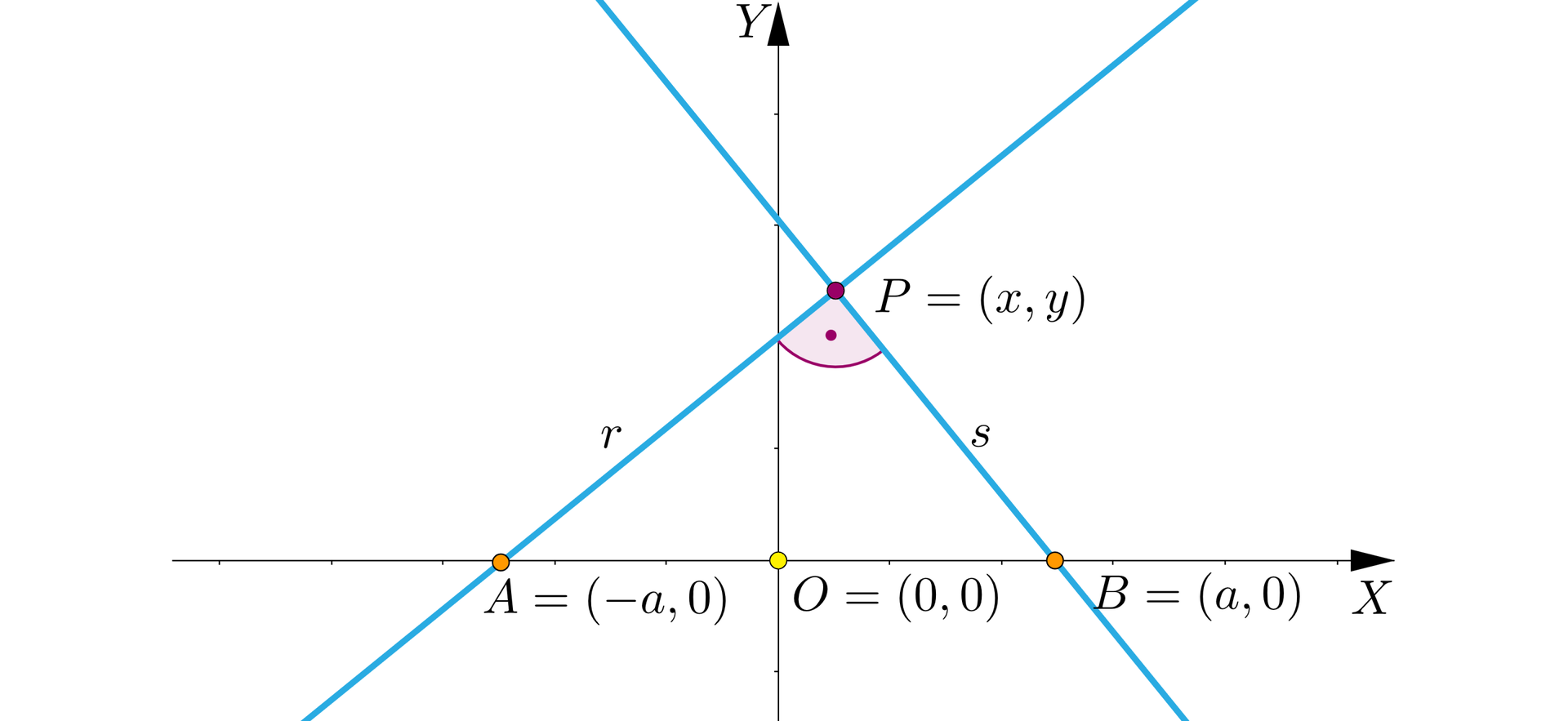
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz z pionową osią Y. Na płaszczyźnie narysowano dwie ukośne proste, które są do siebie prostopadłe. Proste te przecinają się w punkcie P o współrzędnych nawias x przecinek y zamknięcie nawiasu. Punkt ten leży w pierwszej ćwiartce układu. Jedna z prostych przecina ujemną półoś O X w punkcie A o współrzędnych nawias minus a przecinek 0 zamknięcie nawiasu. Odcinek A P oznaczono literą r; druga z prostych przecina dodatnią półoś O X w punkcie B o współrzędnych nawias a przecinek 0 zamknięcie nawiasu. Odcinek B P oznaczono literą s. Zaznaczono również początek układu współrzędnych O równa się nawias 0 przecinek 0 zamknięcie nawiasu.

W tym układzie współrzędnych $A = (- a, 0)$ , $B = (a, 0)$ , $a > 0$ ; ponadto punkt $O$ jest środkiem odcinka $A B$ . Punkt $P$ jest punktem przecięcia prostych prostopadłych $r$ i $s$ .

Równanie prostej $r$ , na której leży punkt $A$ ma postać:

$y = p (x + a)$ ,

zaś równanie prostej $s$ , na której leży punkt $B$ , to:

$y = - \frac{1}{p} (x - a)$ .

By znaleźć współrzędne punktu $P$ , rozwiązujemy układ równań:

$\{\begin{cases} y = p (x + a) \\ y = - \frac{1}{p} (x - a) \end{cases}$

$\{\begin{cases} y = p (x + a) \\ p y = - x + a \end{cases}$

$\{\begin{cases} y = p (x + a) \\ x = a - p y \end{cases}$

$\{\begin{cases} y = p (a - p y + a) \\ x = a - p y \end{cases}$

$\{\begin{cases} y = 2 a p - p^{2} y \\ x = a - p y \end{cases}$

$\{\begin{cases} y (1 + p^{2}) = 2 a p \\ x = a - p y \end{cases}$

$\{\begin{cases} x = \frac{a (1 - p^{2})}{1 + p^{2}} \\ y = \frac{2 a p}{1 + p^{2}} \end{cases}$

Otrzymaliśmy współrzędne punktu $P$ :

$P = (\frac{a (1 - p^{2})}{1 + p^{2}}, \frac{2 a p}{1 + p^{2}})$ .

Jeśli punkt $P$ leży na okręgu o środku w punkcie $O$ , to jego odległość od $O$ musi być równa $a$ .

Sprawdźmy to.

$|O P| = \sqrt{{(\frac{a (1 - p^{2})}{1 + p^{2}} - 0)}^{2} + {(\frac{2 a p}{1 + p^{2}} - 0)}^{2}} = \sqrt{\frac{a^{2} - 2 a^{2} p^{2} + a^{2} p^{4} + 4 a^{2} p^{2}}{{(1 + p^{2})}^{2}}} =$

$= \sqrt{\frac{a^{2} {(1 + p^{2})}^{2}}{{(1 + p^{2})}^{2}}} = \sqrt{a^{2}} = a$ .

Wykazaliśmy więc, że punkt $P$ leży na okręgu, któego promień jest równy połowie długości przeciwprostokątnej .

Przykład 3

Wyznaczymy równanie okręgu opisanego na trójkącie o wierzchołkach $A = (- 2, - 1)$ ; $B = (4, 1)$ ; $C = (2, 3)$ .

Rozwiązanie:

Zauważmy, że trójkąt jest prostokątny, gdyż:

$|A C| = \sqrt{{(2 + 2)}^{2} + {(3 + 1)}^{2}} = \sqrt{32}$ ; $|B C| = \sqrt{{(2 - 4)}^{2} + {(3 - 1)}^{2}} = \sqrt{8}$ ; $|A B| = \sqrt{{(4 + 2)}^{2} + {(1 + 1)}^{2}} = \sqrt{40}$ i ${|A B|}^{2} = {|B C|}^{2} + {|A C|}^{2}$

Zatem środek okręgu opisanego jest środkiem przeciwprostokątnej $A B : S = (\frac{- 2 + 4}{2}, \frac{- 1 + 1}{2})$ , czyli $S = (1, 0)$ . Promień okręgu ma długość $R = \frac{1}{2} \cdot |A B| = \sqrt{10}$ .

Równanie okręgu ma postać: ${(x - 1)}^{2} + y^{2} = 10$ .

Przykład 4

Wyznaczymy równanie okręgu opisanego na trójkącie równobocznym o wierzchołkach $A = (- 2, - 2)$ , $B = (4, - 2)$ , $C = (1, 3 \sqrt{3} - 2)$ .

Rozwiązanie:

Ponieważ trójkąt $A B C$ jest równoboczny, to długość jego promienia jest równa $R = \frac{a \sqrt{3}}{3}$ , gdzie $a$ oznacza długość boku trójkąta. Zauważmy, że $a = 6$ , zatem $R = 2 \sqrt{3}$ .

Wyznaczymy teraz współrzędne środka $S$ tego okręgu. Leży on na symetralnej boku $A B$ , więc $x_{S} = \frac{- 2 + 4}{2} = 1$ .

$|A S| = 2 \sqrt{3}$ , zatem $\sqrt{{(1 + 2)}^{2} + {(y_{S} + 2)}^{2}} = 2 \sqrt{3}$

$9 + {(y_{S} + 2)}^{2} = 12$

${(y_{S} + 2)}^{2} = 3$

$y_{S} + 2 = \sqrt{3}$ lub $y_{S} + 2 = - \sqrt{3}$

$y_{S} = \sqrt{3} - 2$ lub $y_{S} = - \sqrt{3} - 2$

Punkt $S_{1} = (1, - \sqrt{3} - 2)$ nie leży wewnątrz trójkąta $A B C$ , zatem $S = (1, \sqrt{3} - 2)$ .

Równanie okręgu opisanego na trójkącie równobocznym $A B C$ ma postać:

${(x - 1)}^{2} + {(y - \sqrt{3} + 2)}^{2} = 12$

Słownik

symetralna boku trójkąta

prosta prostopadła do boku trójkąta i przechodząca przez jego środek

Wprowadzenie

Galeria zdjęć interaktywnych

Już wiesz

Słownik