Przeczytaj
Przypomnijmy wzory na polapola i obwodyobwody różnych wielokątów.
Trójkąt

gdzie:
Kwadrat
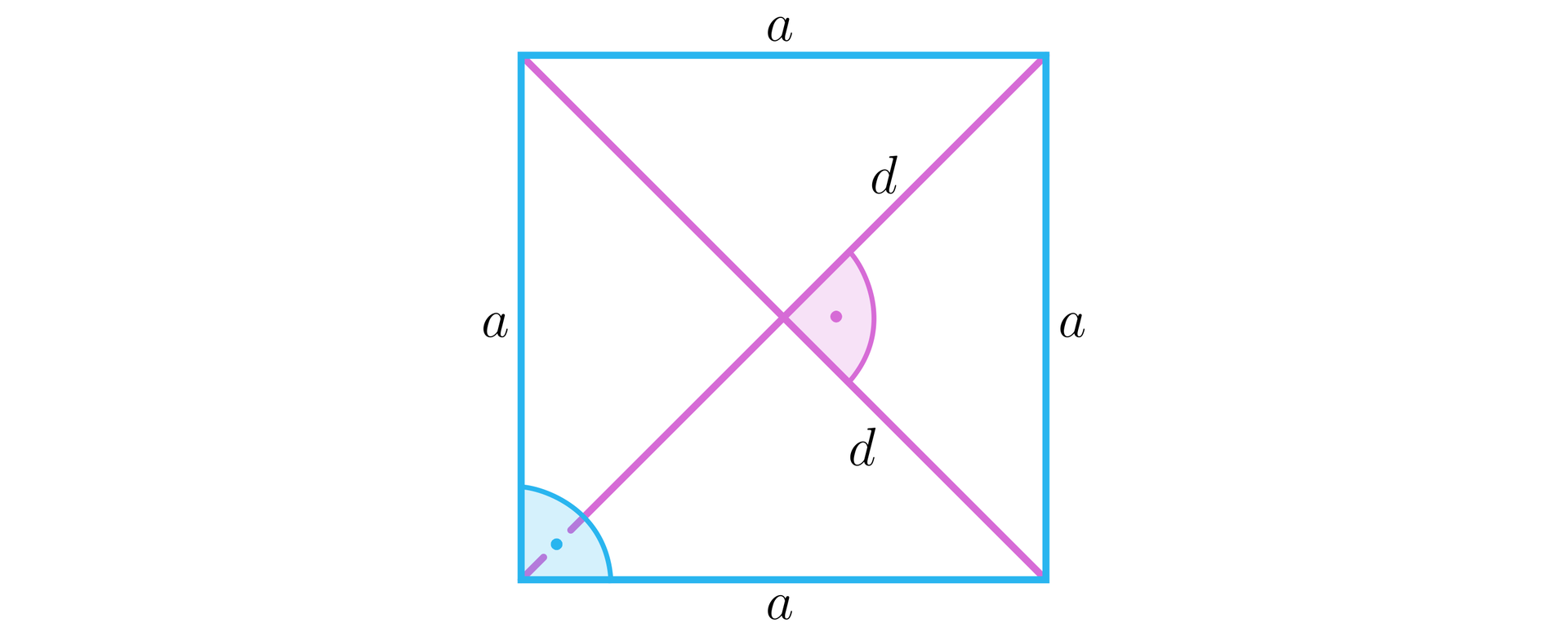
gdzie:
Prostokąt
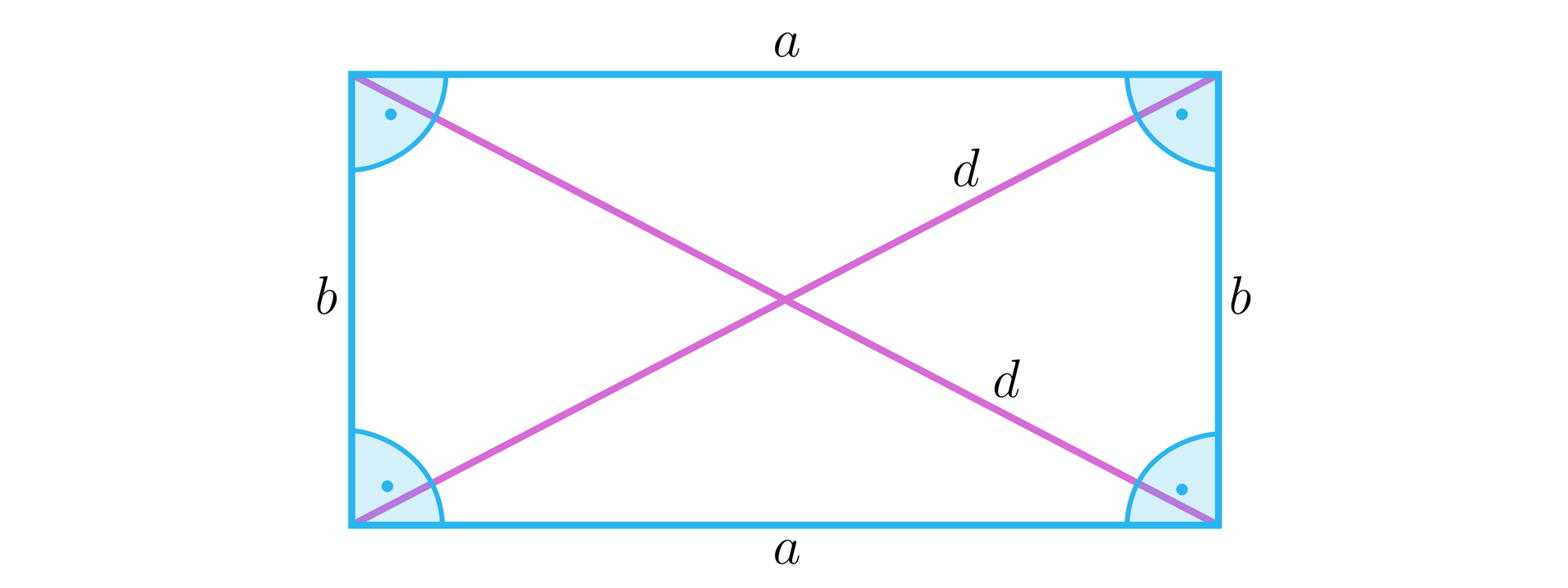
Równoległobok

Romb
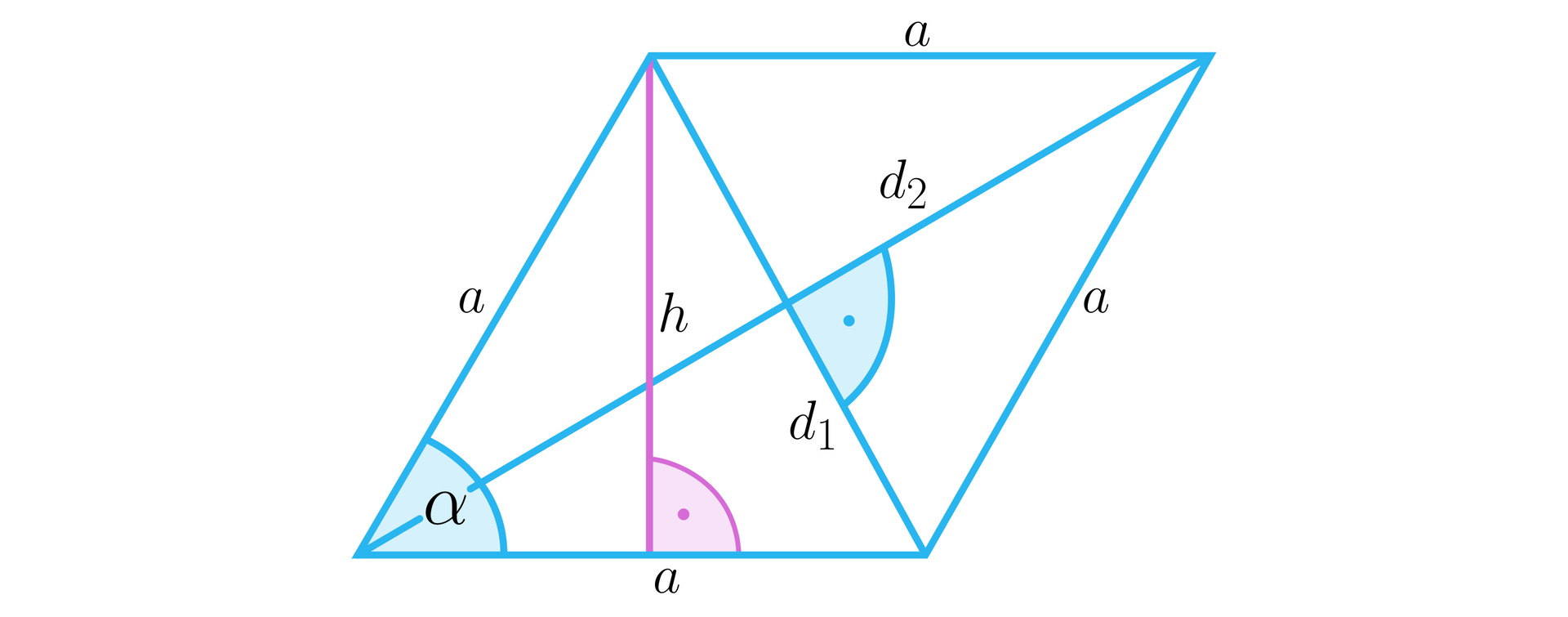
Trapez

Deltoid

Do obliczania pól i obwodów wielokątów wykorzystamy funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym.

W poniższych przykładach omówimy, jak wyznaczać pola i obwody wielokątów z zastosowaniem funkcji trygonometrycznychfunkcji trygonometrycznych.
Tangens kąta ostrego w trójkącie prostokątnym jest równy , a przeciwprostokątna trójkąta ma długość . Wyznaczymy pole i obwód tego trójkąta.
Rozwiązanie:
Jeżeli tangens kąta ostrego w trójkącie prostokątnym jest równy , to narysujmy trójkąt prostokątny i wprowadźmy odpowiednie oznaczenia:
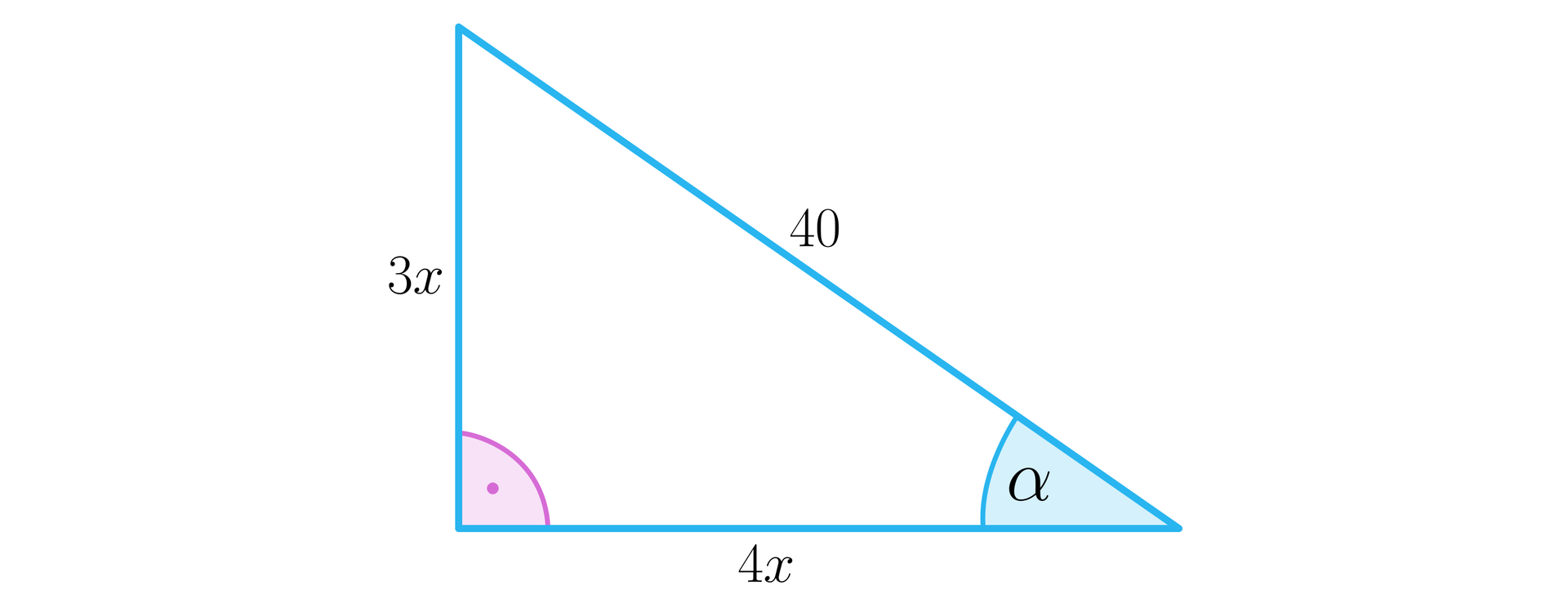
Do wyznaczenia wartości wykorzystamy twierdzenie Pitagorasa. Zatem:
.
Wobec tego .
Przyprostokątne trójkąta mają długości i .
Zatem obwód trójkąta jest równy:
.
Pole trójkąta wynosi:
.
Obliczymy pole i obwód równoległoboku o wymiarach jak na rysunku, jeżeli wiadomo, że .

Rozwiązanie:
Jeżeli , to zachodzi zależność:
, czyli .
Długości odcinków i obliczamy, korzystając z twierdzenia Pitagorasa:
,
.
Zatem podstawa równoległoboku ma długość:
.
Obwód równoległoboku wynosi:
.
Pole równoległoboku jest równe:
.
Wyznaczymy obwód i pole trapezu równoramiennego o kącie ostrym , jeżeli ramię oraz krótsza podstawa mają długość .
Rozwiązanie:
Narysujmy trapez równoramienny i wprowadźmy odpowiednie oznaczenia:

Korzystając z funkcji trygonometrycznych w trójkącie prostokątnym, wyznaczamy długości odpowiednich odcinków:
, więc ,
, więc .
Zauważmy, że , zatem:
.
Pole tego trapezu wynosi:
.
Obwód tego trapezu jest równy:
.
Działka ma kształt trapezu, jak na poniższym rysunku. Obliczymy obwód i pole tej działki.
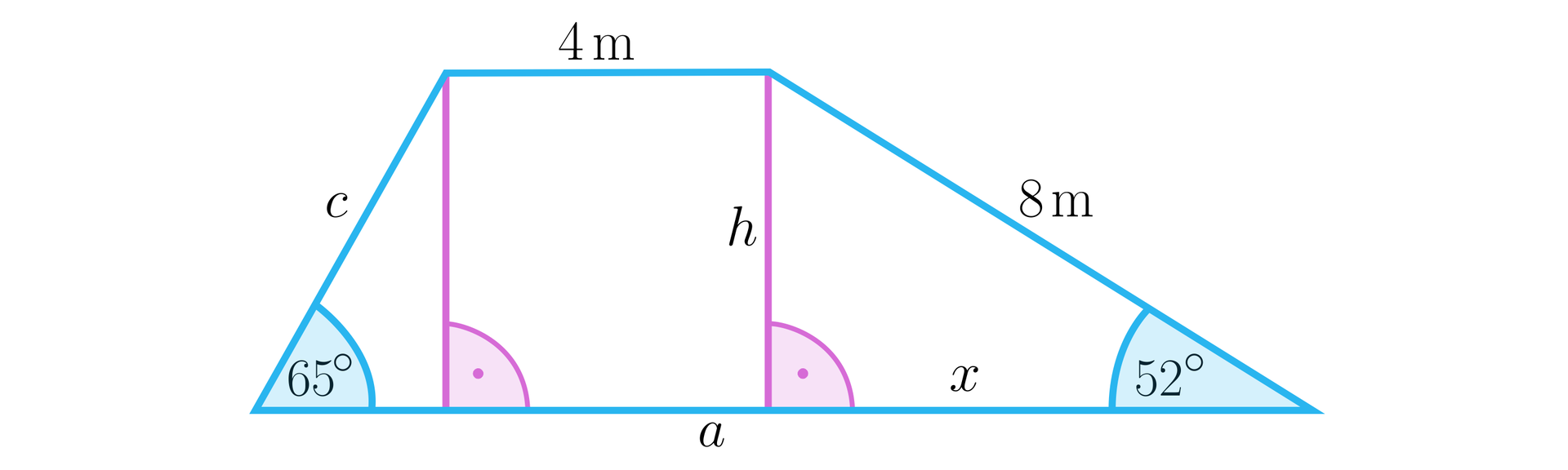
Rozwiązanie:
Do wyznaczenia długości , i użyjemy tablic wartości funkcji trygonometrycznych.
Zatem:
, więc ,
, więc ,
, więc
Korzystając z twierdzenia Pitagorasa, mamy zależność:
, więc .
Długość podstawy trapezu wynosi:
.
Obwód trapezu jest równy:
.
Pole trapezu wynosi:
.
Obliczymy obwód rombu, jeżeli jego pole jest równe , a cosinus kąta ostrego wynosi .
Rozwiązanie:
Narysujmy romb i wprowadźmy odpowiednie oznaczenia:
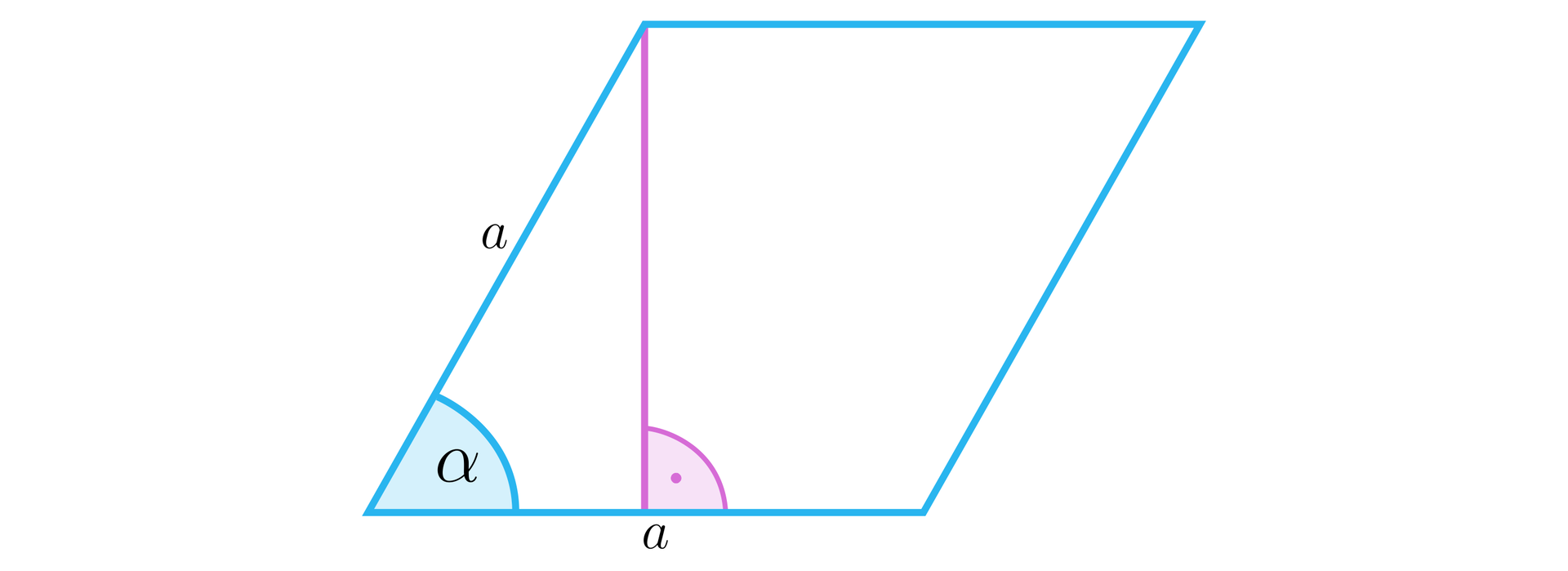
Jeżeli , to korzystając ze wzoru na jedynkę trygonometryczną, obliczamy wartość sinusa tego kąta:
, czyli , bo jest kątem ostrym.
Ze wzoru na pole równoległoboku obliczamy długość boku rombu:
, więc , czyli .
Wobec tego obwód rombu jest równy:
.
Słownik
funkcje wyrażające stosunki między długościami boków trójkąta prostokątnego względem miar jego kątów wewnętrznych
suma długości wszystkich boków wielokąta
suma pól trójkątów, z których zbudowany jest dany wielokąt