Przeczytaj

Twierdzenie Pitagorasa

Twierdzenie: Twierdzenie Pitagorasa

Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym o przyprostokątnych $a$ , $b$ i przeciwprostokątnej $c$ zachodzi następująca równość:

a^{2} + b^{2} = c^{2}

Twierdzenie to pozwala na wyznaczenie długości boku, jeśli znamy długości dwóch pozostałych. Wzór na kwadrat długości przeciwprostokątnej podany jest w twierdzeniu Pitagorasa. Proste przekształcenie równości Pitagorasa daje nam wzory na kwadraty długości przyprostokątnych:

a^{2} = c^{2} - b^{2}

b^{2} = c^{2} - a^{2}

Aby uzyskać długości tych odcinków, należy wyznaczyć pierwiastki z ich kwadratów.

Przykład 1

W trójkącie prostokątnym przeciwprostokątna ma długość $37$ , a jedna z przyprostokątnych ma długość $35$ . Wyznaczymy długość drugiej przyprostokątnej.

Rozwiązanie

$a^{2} = c^{2} - b^{2} = 37^{2} - 35^{2} = 144$ , więc $a = \sqrt{144} = 12$ .

Jeżeli mamy dwa boki $x ⩽ y$ trójkąta prostokątnego, to żeby wyznaczyć trzeci bok, musimy wiedzieć jaką rolę pełnią te boki w trójkącie. Na rysunku mamy dwa różne trójkąty prostokątne zbudowane z odcinków $x$ , $y$ .

R1SrRrk8nD4WN

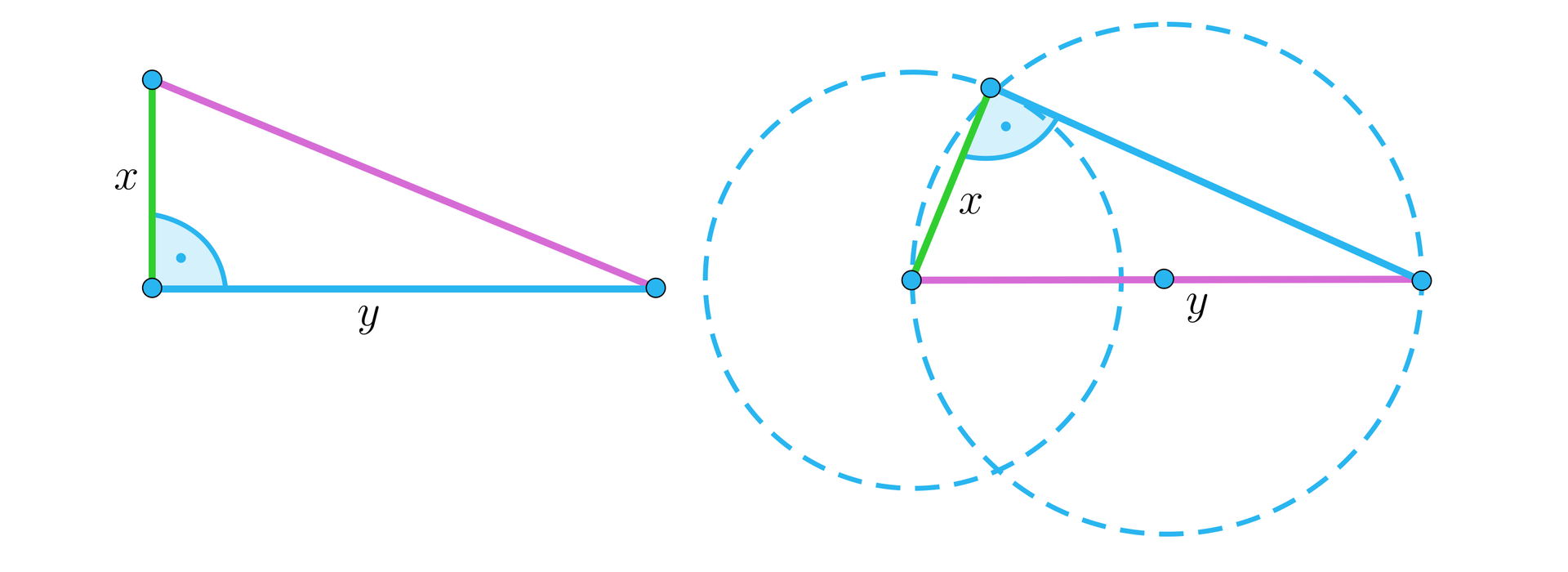
Ilustracja przedstawia trójkąt prostokątny o pionowej przyprostokątnej x oraz poziomej przyprostokątnej y. Obok narysowano trójkąt zbudowany na odcinkach x i y, przy czym x jest przyprostokątną, a y przeciwprostokątną. Zaznaczono środek odcinka y. Jest to również środek okręgu, przy czym y jest średnicą okręgu. Trójkąt wpisany jest okrąg. Lewy koniec odcinka y jest środkiem drugiego, mniejszego okręgu przecinającego się z większym okręgiem. Środek mniejszego okręgu to wspólny koniec odcinków x i y. Odcinek x jest promieniem mniejszego okręgu. Trzeci bok trójkąta jest cięciwą większego okręgu.

Przykład 2

Trójkąt prostokątny ma dwa boki długości $8$ i $15$ . Pokażemy, że istnieją dwa trójkąty prostokątne spełniające ten warunek. Wyznaczymy długość trzeciego boku każdego z nich.

Rozwiązanie

Jeżeli znane boki są przyprostokątnymi, to przeciwprostokątna $c = \sqrt{8^{2} + 15^{2}} = 17$ .

Jeżeli jeden ze znanych boków jest przeciwprostokątną, to jest to dłuższy bok. Wtedy druga przyprostokątna ma długość $\sqrt{15^{2} - 8^{2}} = \sqrt{161}$ .

Przykład 3

Długości boków trójkąta prostokątnego są liczbami całkowitymi opisanymi za pomocą wyrażeń: $x$ , $2 x - 10$ , $2 x - 1$ . Wyznaczymy długości tych boków.

Rozwiązanie

Najpierw przeanalizujmy warunki, jakie powinna spełniać zmienna $x$ .

Ponieważ podane wyrażenia odnoszą się do długości boków, to $x > 0$ , $2 x - 10 > 0$ , więc $x > \frac{10}{2} = 5$ oraz $2 x - 1 > 0$ , więc $x > \frac{1}{2}$ . Stąd $x > 5$ .

Załóżmy, że:

1. odcinek o długości $x$ jest przeciwprostokątną.

Wtedy $x^{2} = {(2 x - 10)}^{2} + {(2 x - 1)}^{2} = 4 x^{2} - 40 x + 100 + 4 x^{2} - 4 x + 1$ .

$- 7 x^{2} + 44 x - 101 = 0$

$∆ = 44^{2} - 4 \cdot 7 \cdot 101 < 0$ – brak rozwiązań.

2. odcinek o długości $2 x - 10$ jest przeciwprostokątną.

Wtedy ${(2 x - 10)}^{2} = x^{2} + {(2 x - 1)}^{2}$

$4 x^{2} - 40 x + 100 = x^{2} + 4 x^{2} - 4 x + 1$

$- x^{2} - 36 x + 99 = 0$

$∆ = 36^{2} + 4 \cdot 99 = 1692$

$\sqrt{∆} = \sqrt{1692} = 6 \sqrt{47}$

Pierwiastki równania nie są liczbami całkowitym, bo $\sqrt{∆}$ jest liczbą niewymierną, a współczynniki równania są liczbami całkowitymi.

3. odcinek o długości $2 x - 1$ jest przeciwprostokątną.

Wtedy ${(2 x - 1)}^{2} = x^{2} + {(2 x - 10)}^{2}$

$4 x^{2} - 4 x + 1 = x^{2} + 4 x^{2} - 40 x + 100$

$- x^{2} + 36 x - 99 = 0$

$∆ = 36^{2} - 4 \cdot 99 = 900$

$\sqrt{∆} = \sqrt{900} = 30$

$x_{1} = \frac{- 36 - 30}{- 2} = 33 > 5$

Długości boków tego trójkąta, to:

$x = 33$

$2 x - 10 = 56$

$2 x - 1 = 65$

$x_{2} = \frac{- 36 + 30}{- 2} = 3 < 5$ – nie spełnia wymagań.

Długości boków tego trójkąta są równe: $33, 56, 65$ .

Przykład 4

Trójkąt prostokątny ma boki długości $x$ , $3 x - 10$ , $2 x - 1$ . Wyznaczymy długości tych boków.

Rozwiązanie

Najpierw przeanalizujmy warunki, jakie powinna spełniać zmienna $x$ .

Ponieważ podane wyrażenia odnoszą się do długości boków, to

$x > 0$ , $3 x - 10 > 0$ , więc $x > \frac{10}{3}$ oraz $2 x - 1 > 0$ , więc $x > \frac{1}{2}$ . Stąd $x > \frac{10}{3}$ .

Załóżmy, że

1. odcinek o długości $x$ jest przeciwprostokątną.

Wtedy

$x^{2} = {(3 x - 10)}^{2} + {(2 x - 1)}^{2} = 9 x^{2} - 60 x + 100 + 4 x^{2} - 4 x + 1 =$

$= 13 x^{2} - 64 x + 101$

$- 12 x^{2} + 64 x - 101 = 0$

$∆ = 64^{2} - 4 \cdot 12 \cdot 101 < 0$ – brak rozwiązań.

2. odcinek o długości $3 x - 10$ jest przeciwprostokątną.

Wtedy ${(3 x - 10)}^{2} = x^{2} + {(2 x - 1)}^{2}$

$9 x^{2} - 60 x + 100 = x^{2} + 4 x^{2} - 4 x + 1$

$4 x^{2} - 56 x + 99 = 0$

$∆ = 56^{2} - 4 \cdot 4 \cdot 99 = 1552$

$\sqrt{∆} = \sqrt{1552} = 4 \sqrt{97}$

$x_{1} = \frac{56 - 4 \sqrt{97}}{2 \cdot 4} = 7 - \frac{\sqrt{97}}{2} < \frac{10}{3}$ – nie spełnia wymagań,

$x_{2} = \frac{56 + 4 \sqrt{97}}{2 \cdot 4} = 7 + \frac{\sqrt{97}}{2} > \frac{10}{3}$ – jest rozwiązaniem.

Długości boków tego trójkąta, to

$x = 7 - \frac{\sqrt{97}}{2}$

$3 x - 10 = 11 - \frac{3 \sqrt{97}}{2}$

$2 x - 1 = 13 - \sqrt{97}$

3. odcinek o długości $2 x - 1$ jest przeciwprostokątną. Przeliczenia wykonujemy analogicznie do warunku $2$ a długości boków tego trójkąta to:

$x = \frac{28 + \sqrt{190}}{6}$

$3 x - 10 = \frac{8 + \sqrt{190}}{2}$

$2 x - 1 = \frac{25 + \sqrt{190}}{3}$

Zatem długości boków trójkąta wynoszą: $7 - \frac{\sqrt{97}}{2}; 11 - \frac{3 \sqrt{97}}{2}; 13 - \sqrt{97}$ lub $\frac{28 + \sqrt{190}}{6}; \frac{8 + \sqrt{190}}{2}; \frac{25 + \sqrt{190}}{3}$

Jednym z najważniejszych odcinków w trójkącie jest wysokość trójkąta. W każdym trójkącie przynajmniej jedna wysokość leży wewnątrz trójkąta.

Przykład 5

W trójkącie równoramiennym dana jest wysokość $h$ opuszczona na podstawę trójkąta oraz ramię $a$ .

RB7XJfy2Z6oFB

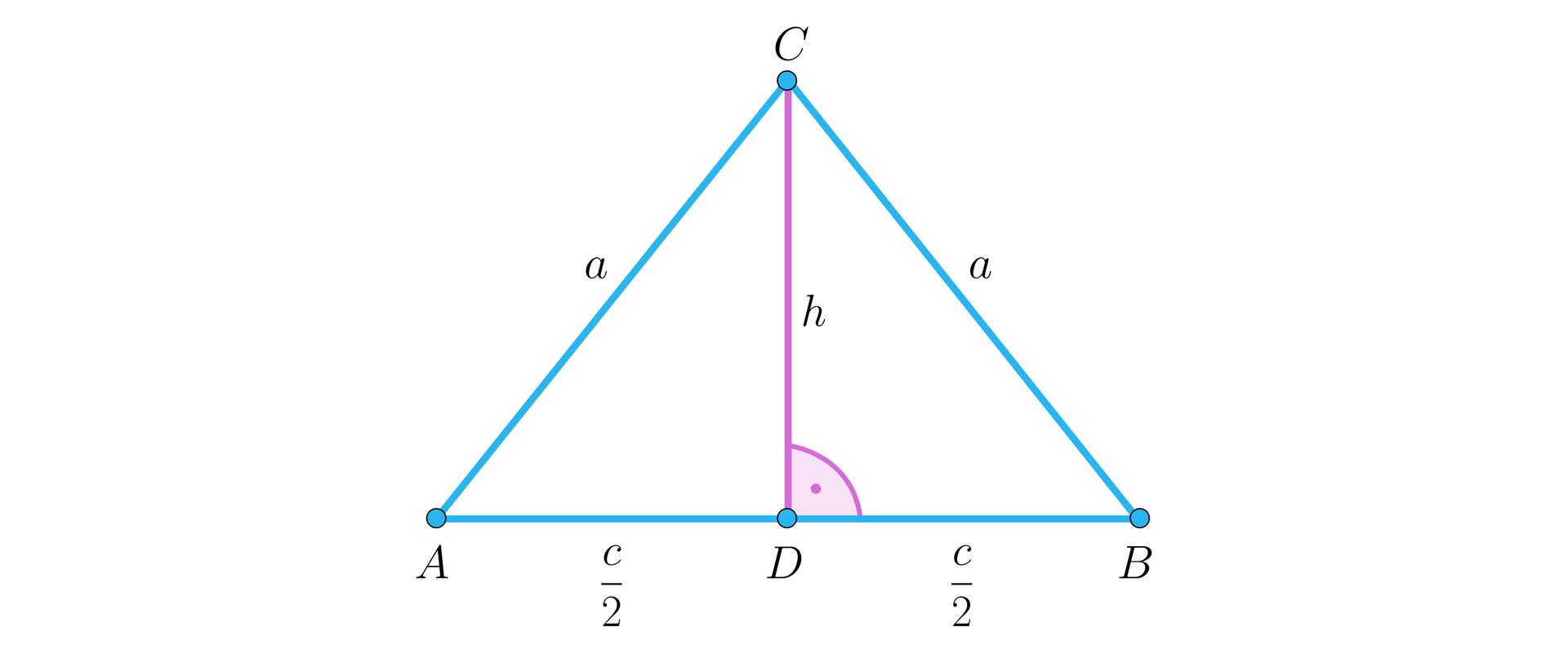
Na ilustracji przedstawiono trójkąt równoramienny o ramionach długości a, oraz podstawie długości c. Z wierzchołka C, opuszczono wysokość h na podstawę AB, której spodek leżt w punkcie D. Wysokość podzieliła podstawę trójkąta na dwa równe odcinki o długości c2.

Wyznaczymy wzór na obwód tego trójkąta.

Rozwiązanie

Wykorzystamy własność, że wysokość opuszczona na podstawę trójkąta równoramiennego dzieli podstawę $c$ na połowy.

Wtedy ${(\frac{c}{2})}^{2} = a^{2} - h^{2}$ , więc $c = 2 \sqrt{a^{2} - h^{2}}$ .

Zatem obwód jest równy $2 a + c = 2 a + 2 \sqrt{a^{2} - h^{2}}$ .

Przykład 6

W trójkącie $A B C$ spodek $D$ wysokości opuszczonej na bok $A B$ dzieli ten bok tak, że $|A D| : |D B| = 2 : 1$ . Długość wysokości $h = 2$ , a długość boku $|A C| = 2 \sqrt{5}$ . Wyznaczymy pole tego trójkąta.

Rozwiązanie

Wysokość dzieli trójkąt na dwa trójkąty prostokątne $A C D$ i $B C D$ .

Wtedy ${|A D|}^{2} = {|A C|}^{2} - h^{2} = 20 - 4 = 16$ .

$|A D| = \sqrt{16} = 4$

$|D B| = \frac{|A D|}{2} = 2$ , stąd $|A B| = 6$

Pole trójkąta wynosi $P = \frac{6 \cdot 2}{2} = 6$ .

Wyznaczanie długości środkowych w trójkącie prostokątnym

Na rysunku przedstawiony jest trójkąt prostokątny i jego środkowe oznaczone różnymi kolorami.

R10UYRso6niqV

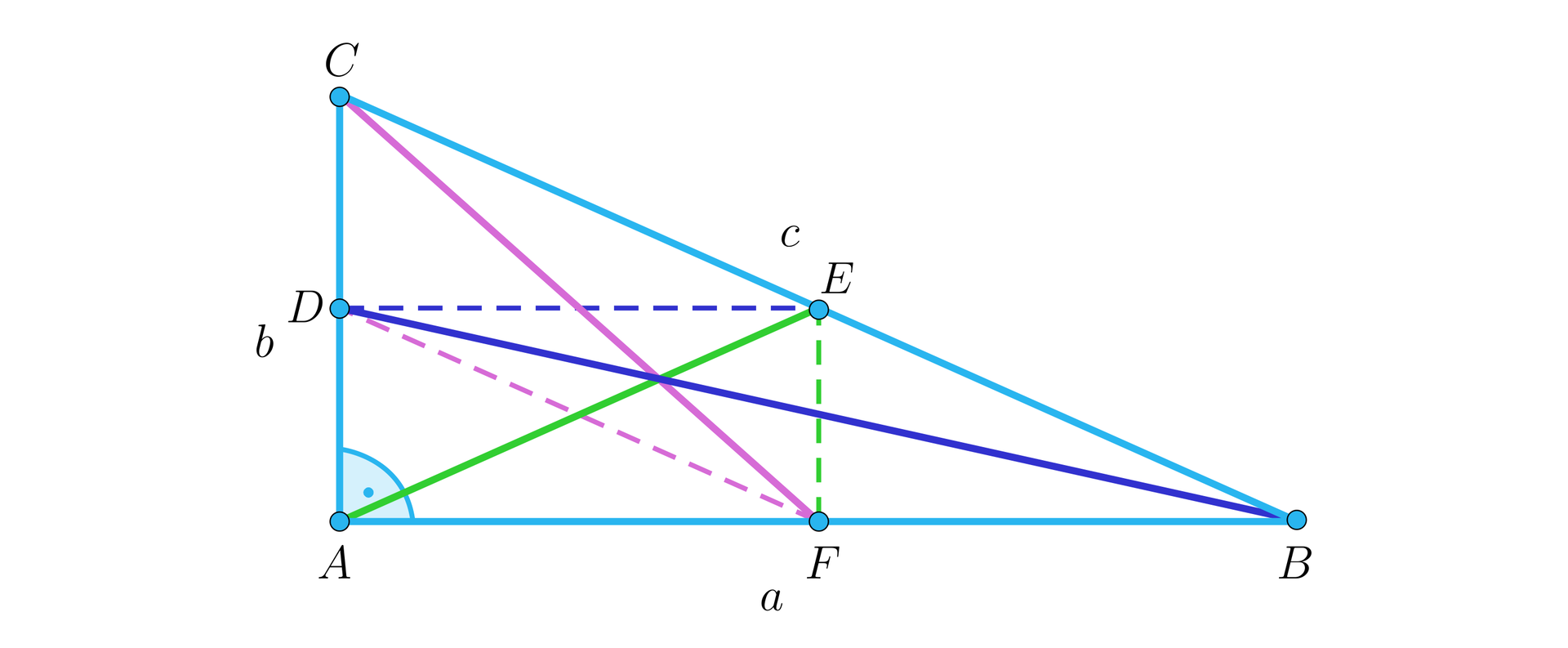
Na ilustracji przedstawiono trójkąt ABC z kątem prostym przy wierzchołku A. Zaznaczono środki boków trójkąta, oraz połączono je z wierzchołkami leżącymi naprzeciw. Punkt D stanowi środkową przyprostokątnej AC i połączono go z wierzchołkiem B. Punkt F stanowi środkową przyprostokątnej AB i połączono go z wierzchołkiem C. Punkt E stanowi środkową przeciwprostokątnej BC i połączono go z wierzchołkiem A. Linią przerywaną połączono punkty D, E i F.

Odcinki oznaczone liniami przerywanymi łączą środki boków. Z własności linii środkowej w trójkącielinia środkowa w trójkącielinii środkowej w trójkącie, odcinki te są równoległe do odpowiednich boków i mają długości równe połowie długości odpowiednich boków.

Wyznaczymy długość środkowejśrodkowa w trójkącieśrodkowej $A E$ .

Zauważamy, że $A E$ jest przeciwprostokątną trójkąta $A E F$ , bo $E F ∥ A C$ . Ponadto, $|E F| = \frac{b}{2}$ i $|A F| = \frac{a}{2}$ .

Stąd ${|A E|}^{2} = {(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2} = \frac{a^{2} + b^{2}}{4} = \frac{c^{2}}{4}$ , więc $|A E| = \frac{c}{2}$ .

Długość środkowej $C F$ wyznaczamy jako długość przeciwprostokątnej trójkąta prostokątnego $A C F$ .

Stąd ${|C F|}^{2} = {(\frac{a}{2})}^{2} + b^{2} = \frac{a^{2} + 4 b^{2}}{4}$ , więc $|C F| = \sqrt{\frac{a^{2} + 4 b^{2}}{4}} = \frac{\sqrt{c^{2} + 3 b^{2}}}{2}$ .

Przykład 7

Jedna z przyprostokątnych trójkąta prostokątnego ma długość $a$ i jest pięć razy krótsza od przeciwprostokątnej. Wyznaczymy długość środkowej poprowadzonej do dłuższej przyprostokątnej.

Rozwiązanie

Wyznaczamy długość $x$ drugiej przyprostokątnej korzystając z twierdzenia Pitagorasa:

$x^{2} = {(5 a)}^{2} - a^{2} = 24 a^{2}$ , stąd $x = 2 \sqrt{6} a$

Zauważamy, że $x > a$ , więc to przyprostokątna długości $x$ jest dłuższa.

Korzystając z wyliczeń w materiale powyżej długość środkowej poprowadzonej do dłuższej przyprostokątnej wynosi $\frac{\sqrt{c^{2} + 3 b^{2}}}{2} = \frac{\sqrt{25 a^{2} + 3 a^{2}}}{2} = \frac{2 \sqrt{7 a^{2}}}{2} = a \sqrt{7}$ .

Wyznaczanie długości wysokości w dowolnym trójkącie

Wyznaczymy długość wysokości leżącej wewnątrz trójkąta korzystając z twierdzenia Pitagorasa.

Na rysunku przedstawione są oznaczenia, które wykorzystamy do wyprowadzenia wzoru na wysokość trójkąta.

R15yQOeq3lUxy

Na ilustracji przedstawiono trójkąt ABC, o ramionach długości b i c, oraz podstawie długości c. Z wierzchołka C opuszczono wysokość h, do podstawy AB, której spodek leży w punkcie D. Wysokość podzieliła podstawę na odcinki długości x i y, oraz na dwa trójkąty prostokątne. Trójkąt pierwszy o bokach długości x,h i c. Trójkąt drugi o bokach długości h, y oraz a.

Wysokość dzieli trójkąt na dwa trójkąty prostokątne $A D C$ o bokach $x$ , $h$ , $b$ oraz $B D C$ o bokach $y$ , $h$ , $a$ .

Stąd $b^{2} = x^{2} + h^{2}$ oraz $a^{2} = y^{2} + h^{2}$ . Odejmując te równania stronami, dostaniemy

$b^{2} - a^{2} = x^{2} + h^{2} - y^{2} - h^{2} = x^{2} - y^{2} = x^{2} - {(c - x)}^{2} =$

$= x^{2} - c^{2} + 2 c x - x^{2} = 2 c x - c^{2}$

Stąd $x = \frac{b^{2} - a^{2} + c^{2}}{2 c}$ . Otrzymany wynik wstawiamy do pierwszego równania

$b^{2} = {(\frac{b^{2} - a^{2} + c^{2}}{2 c})}^{2} + h^{2}$ , więc stosując wzory skróconego mnożenia mamy

$h^{2} = b^{2} - {(\frac{b^{2} - a^{2} + c^{2}}{2 c})}^{2} = (b - \frac{b^{2} - a^{2} + c^{2}}{2 c}) \cdot (b + \frac{b^{2} - a^{2} + c^{2}}{2 c}) =$

$= \frac{(2 b c - b^{2} + a^{2} - c^{2}) (2 b c + b^{2} - a^{2} + c^{2})}{4 c^{2}} = \frac{(a^{2} - (b^{2} - 2 b c + c^{2})) ((2 b c + b^{2} + c^{2}) - a^{2})}{4 c^{2}} =$

$= \frac{(a^{2} - {(b - c)}^{2}) ({(b + c)}^{2} - a^{2})}{4 c^{2}} = \frac{(a + b - c) (a - b + c) (b + c - a) (b + c + a)}{4 c^{2}}$

Ostatecznie $h = \frac{\sqrt{(a + b - c) (a - b + c) (b + c - a) (b + c + a)}}{2 c}$ .

Trójkąt egipski, to trójkąt prostokątny o bokach będących liczbami całkowitymi, pozostającymi w stosunku $3 : 4 : 5$ . Pole tego trójkąta, dla pewnego $a > 0$ , wynosi $P = \frac{3 a \cdot 4 a}{2} = 6 a^{2}$ , a długość wysokości opuszczonej na przeciwprostokątną jest równa $h = \frac{2 P}{5 a} = \frac{12 a^{2}}{5 a} = \frac{12}{5} a$ .

Przykład 8

W oparciu o wyprowadzony wzór na wysokość wyznaczymy długość wysokości opuszczonej na przeciwprostokątną trójkąta egipskiego o bokach długości $3, 4, 5$ .

Rozwiązanie

W tym trójkącie najdłuższy bok ma długość $5$ , więc $c = 5$ , $a = 3$ , $b = 4$ .

Wyznaczamy $h = \frac{\sqrt{(3 + 4 - 5) (3 - 4 + 5) (4 + 5 - 3) (4 + 5 + 3)}}{2 \cdot 5} = \frac{\sqrt{576}}{10} = \frac{\sqrt{9 \cdot 64}}{10} = \frac{3 \cdot 8}{10} = \frac{12}{5}$

Wprowadźmy oznaczenie $p = \frac{a + b + c}{2}$ na połowę obwodu trójkąta $A B C$ o bokach $a$ , $b$ , $c$ i zastosujmy we wzorze na wysokość trójkąta. Oznaczmy boki trójkąta tak, żeby $c$ było najdłuższym bokiem.

Wtedy

$a + b - c = a + b + c - 2 c = 2 p - 2 c = 2 (p - c)$

$a + c - b = a + b + c - 2 b = 2 p - 2 b = 2 (p - b)$

$b + c - a = a + b + c - 2 a = 2 p - 2 a = 2 (p - a)$

$a + b + c = 2 p$

Po wstawieniu do wzoru na wysokość opuszczoną na bok $c$ , dostajemy

$h = \frac{\sqrt{(a + b - c) (a - b + c) (b + c - a) (b + c + a)}}{2 c} =$

$= \frac{\sqrt{2 (p - c) \cdot 2 (p - b) \cdot 2 (p - a) \cdot 2 p}}{2 c} = \frac{4 \sqrt{p (p - a) (p - b) (p - c)}}{2 c} = \frac{2 \sqrt{p (p - a) (p - b) (p - c)}}{c}$

Wyprowadzony wzór pozwala na sformułowanie wzoru na pole trójkąta.

Wzór Herona

Twierdzenie: Wzór Herona

Pole trójkąta o bokach $a$ , $b$ , $c$ jest równe $P = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $p$ jest połową obwodu trójkąta.

Dowód

P = \frac{c \cdot h}{2} = \sqrt{p (p - a) (p - b) (p - c)}

Przykład 9

Wyznaczymy pole trójkąta o bokach $6$ , $8$ , $12$ .

Rozwiązanie

$p = \frac{6 + 8 + 12}{2} = 13$

korzystając ze wzoru Heronawzór Heronawzoru Herona

$P = \sqrt{13 \cdot 7 \cdot 5 \cdot 1} = \sqrt{455}$

Słownik

wzór Herona

wzór, który pozwala na wyznaczenie pola trójkąta na podstawie długości jego boków; pole trójkąta o bokach $a$ , $b$ , $c$ jest równe $P = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $p$ jest połową obwodu trójkąta

linia środkowa w trójkącie

odcinek, który łączy środki boków trójkąta

środkowa w trójkącie

odcinek w trójkącie, który łączy wierzchołek trójkąta ze środkiem przeciwległego boku

Wprowadzenie

Animacja

Wyznaczanie długości środkowych w trójkącie prostokątnym

Wyznaczanie długości wysokości w dowolnym trójkącie

Słownik