Przeczytaj
Walec opisany na stożku
Wyobraźmy sobie walec opisany na stożku. Zastanówmy się: jakie warunki muszą być spełnione, aby walec opisać na stożku? W jaki sposób wykreślić walec opisany na stożku na kartce papieru?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DirTtFk
Zapamiętaj
Walec jest opisany na stożku wtedy i tylko wtedy, gdy podstawa stożka jest jedną z podstaw walca, a wierzchołek stożka jest środkiem drugiej podstawy walca.
Zadania dotyczące walca opisanego na stożku można sprowadzić do prostych zadań geometrii płaskiej. Na rysunku poniżej przedstawiono przekrój osiowy walcaprzekrój osiowy walca opisanego na stożku. Przekrój ten pomoże nam w planowaniu strategii rozwiązania wielu zadań geometrii przestrzennej.
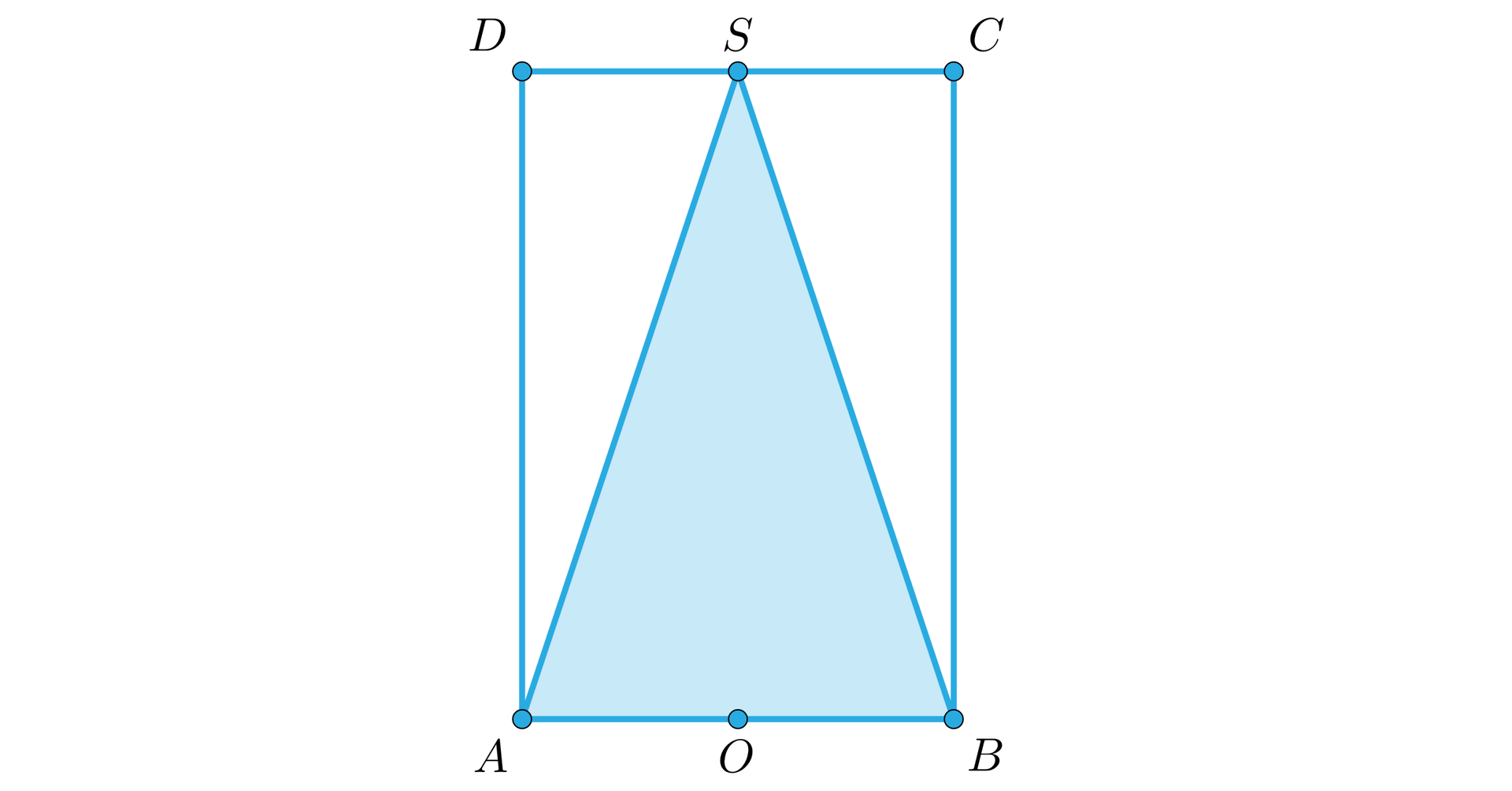
Zauważmy, że długość promienia podstawy walca opisanego na stożku, jest równa długości promienia podstawy stożka i podobnie długość wysokości walca jest równa długości wysokości tego stożka.
Do rozwiązania zadań dotyczących walca opisanego na stożku wykorzystamy znane nam twierdzenia geometrii płaskiej: twierdzenie Pitagorasa oraz twierdzenie cosinusów, wykorzystamy także zależność dla cosinusa kąta podwojonegocosinusa kąta podwojonego.
W walec o promieniu podstawy długości i wysokości wpisano stożek. Obliczmy pole powierzchni bocznej stożka.
Rozwiązanie
1) Wykonujemy rysunek przedstawiający tę sytuację. Wygodnie jest narysować przekrój osiowyprzekrój osiowy odpowiednio ułożonych brył. Rysunek powinien być czytelny.
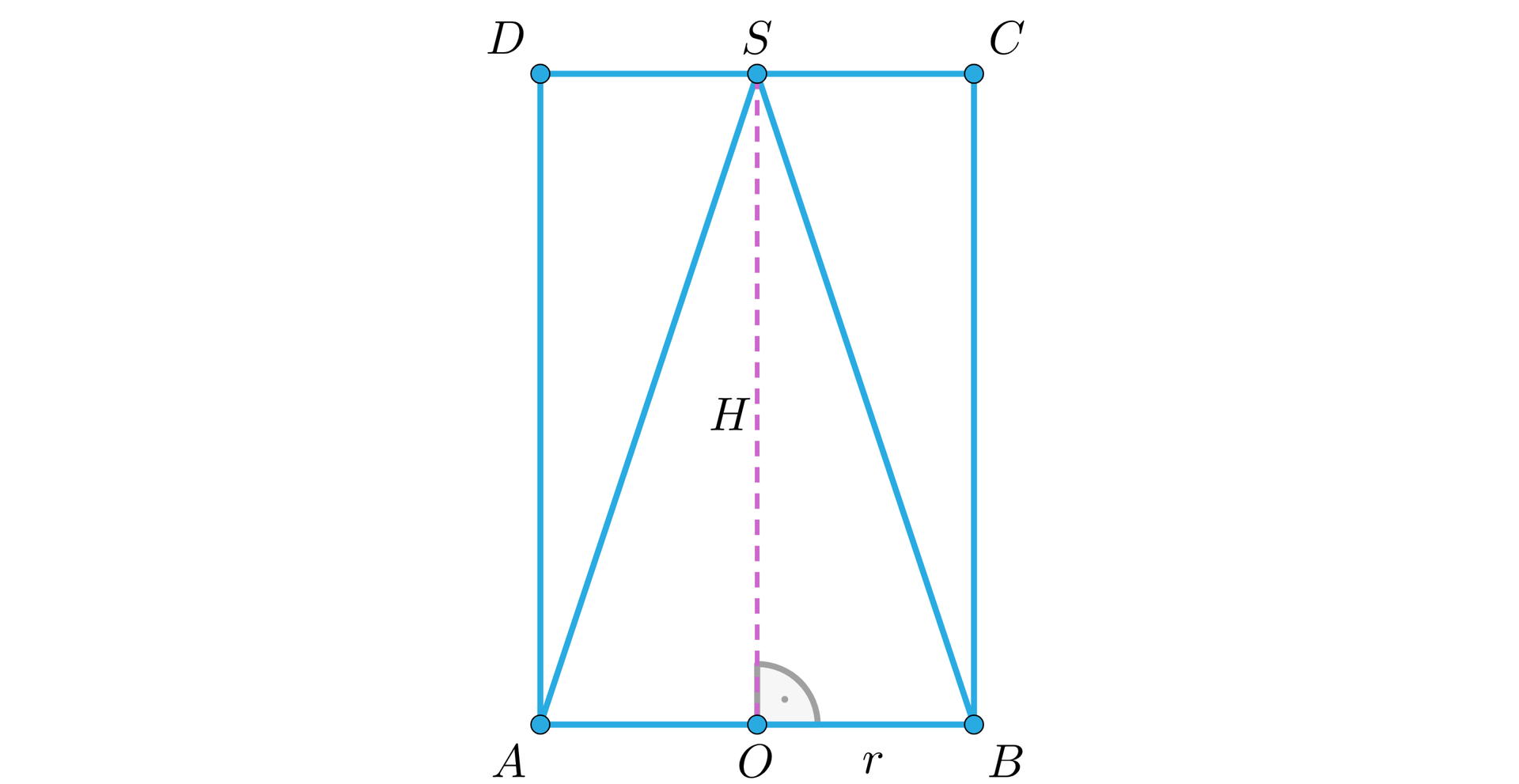
2) Przyjmujemy oznaczenia.
długość promienia podstawy walca i stożka,
długość wysokości walca i stożka.
3) Pole powierzchni bocznej stożka obliczymy ze wzoru , gdzie oznacza długość tworzącej stożka, w tym przypadku to długość odcinka .
4) Z trójkąta i twierdzenia Pitagorasa mamy , zatem , stąd .
5) Pole boczne stożka wynosi .
W walec wpisano stożek. Tworząca stożka ma długość a średnica podstawy walca ma długość . Wyznaczmy cosinus kąta rozwarcia stożka. Uzasadnimy, że jest to kąt rozwarty.
Rozwiązanie
1) Wykonujemy czytelny rysunek. Wystarczy narysować przekrój osiowy tych brył.
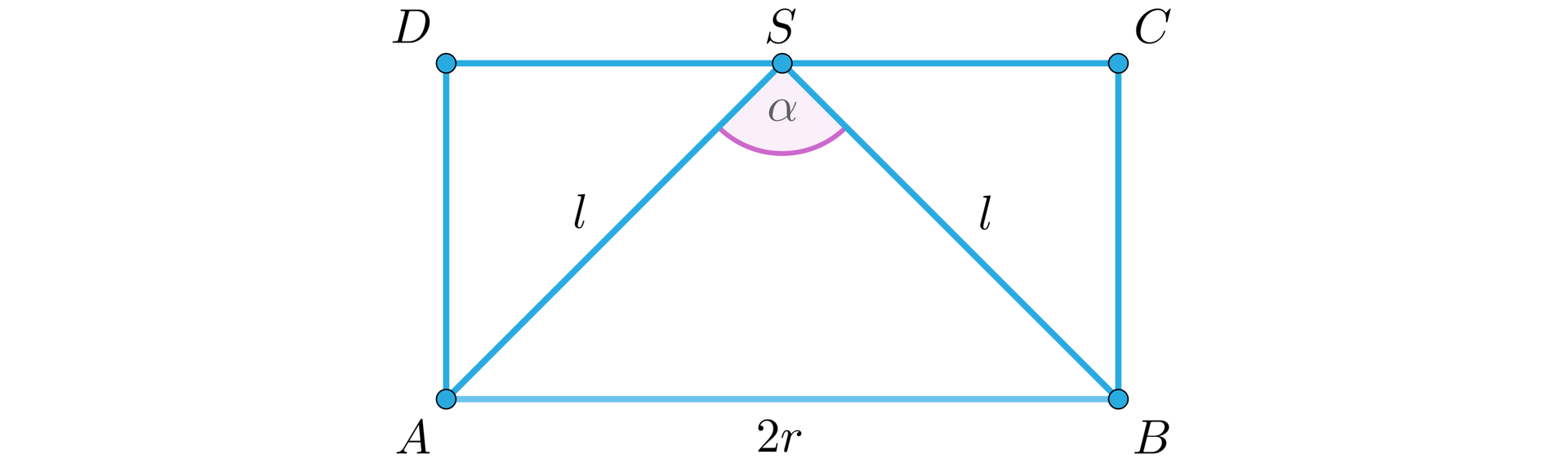
2) Przyjmijmy oznaczenia:
długość średnicy podstawy walca i podstawy stożka,
długość tworzącej stożka.
Zadanie możemy rozwiązać dwoma sposobami:
sposób:
Z trójkąta i twierdzenia cosinusówtwierdzenia cosinusów wyznaczymy kąt rozwarcia stożka .
Mamy zatem , po podstawieniu otrzymujemy odpowiednio . Stąd .
Ponieważ , to kąt rozwarcia stożka jest kątem rozwartym.
sposób:
Poprowadźmy wysokość stożka , gdzie punkt jest środkiem podstawy stożka.

Zauważmy, że kąt i ze wzoru na cosinus kąta podwojonego mamy oraz trójkąta mamy . Wynika stąd, że .
Ponieważ , to kąt rozwarcia stożka jest kątem rozwartym.
W walec wpisano stożek. Kąt rozwarcia stożka jest kątem prostym, zaś wysokość walca ma długość . Obliczmy różnicę pomiędzy polem powierzchni całkowitej walca i polem powierzchni całkowitej stożka.
Rozwiązanie
Rysujemy przekrój osiowy bryły.
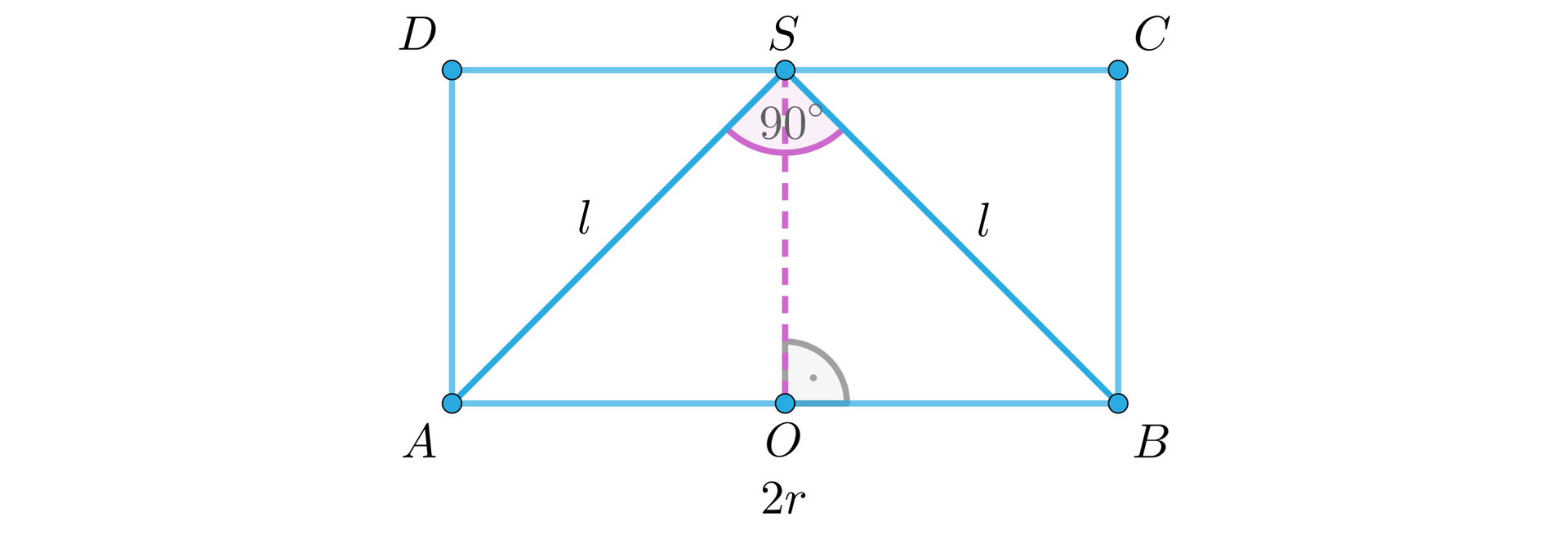
Przyjmujemy oznaczenia.
długość podstawy stożka i walca,
długość wysokości walca i stożka,
długość tworzącej stożka,
miara kąta rozwarcia stożka.
Zauważmy, że trójkąt jest trójkątem równoramiennym, zatem i .
Pole powierzchni całkowitej walca obliczymy ze wzoru , stąd .
Pole powierzchni całkowitej stożka obliczymy ze wzoru , .
Różnica pomiędzy polem powierzchni całkowitej walca a polem powierzchni całkowitej stożka wynosi .
W walec wpisano stożek o wysokości długości . Pole powierzchni bocznej stożka jest równe polu powierzchni bocznej walca. Wyznaczmy objętość walca.
Rozwiązanie
Rysujemy przekrój osiowy bryły.
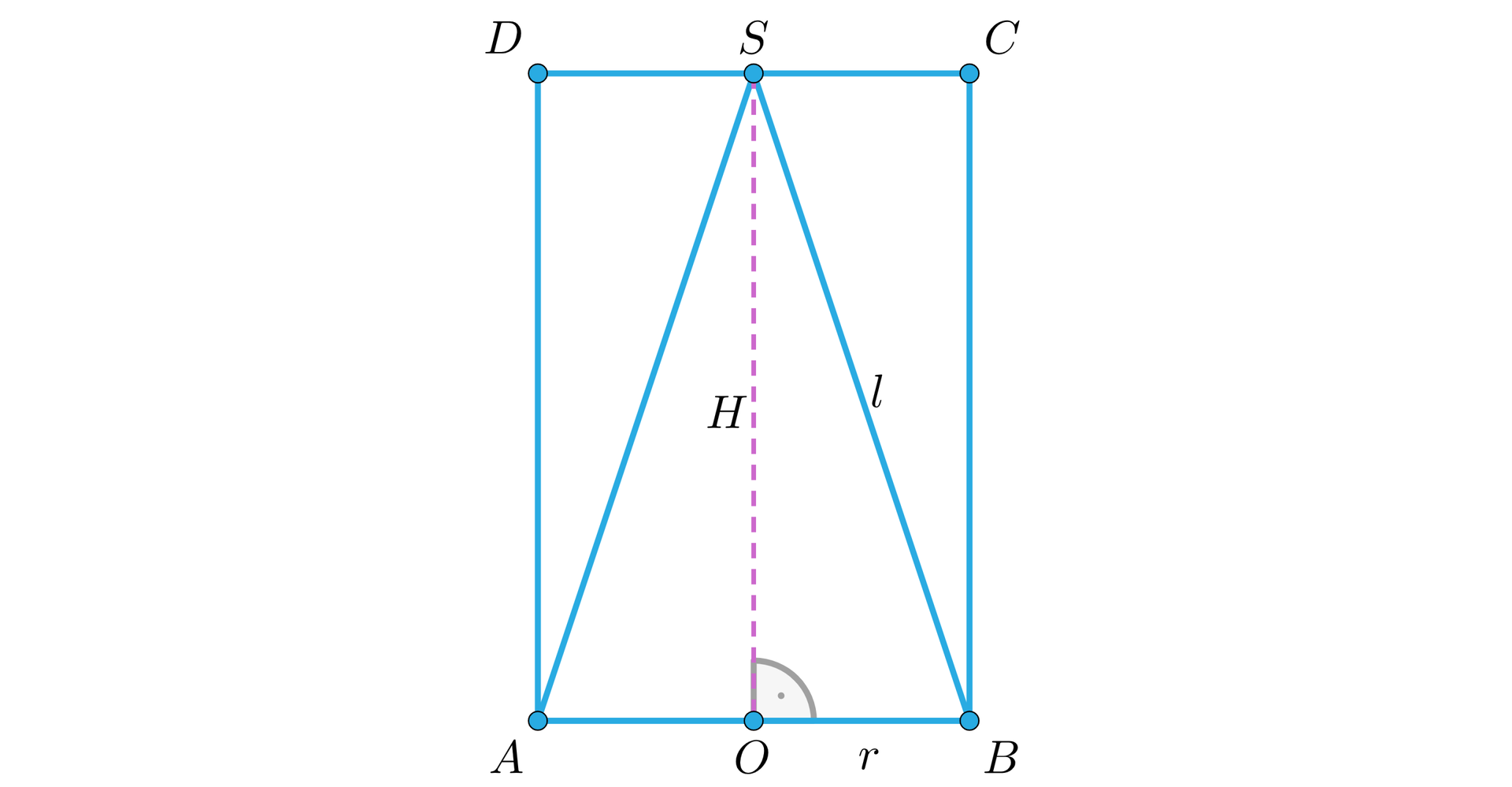
Przyjmujemy oznaczenia.
długość podstawy stożka i walca,
długość wysokości walca i stożka,
długość tworzącej stożka.
Pole powierzchni bocznej walca wyrażamy wzorem oraz pole powierzchni bocznej stożka wzorem .
Z warunków zadania otrzymujemy zależność , stąd mamy .
Objętość walca obliczymy ze wzoru . Zauważmy, że z twierdzenia Pitagorasa dla trójkąta mamy .
Zatem z układu warunków i otrzymujemy , a stąd .
Objętość walca zatem jest równa .
W walec wpisano stożek. Pole powierzchni bocznej stożka jest równe polu powierzchni bocznej walca. Wyznaczmy miarę kąta rozwarcia stożka.
Rozwiązanie
Rysujemy przekrój osiowy bryły.
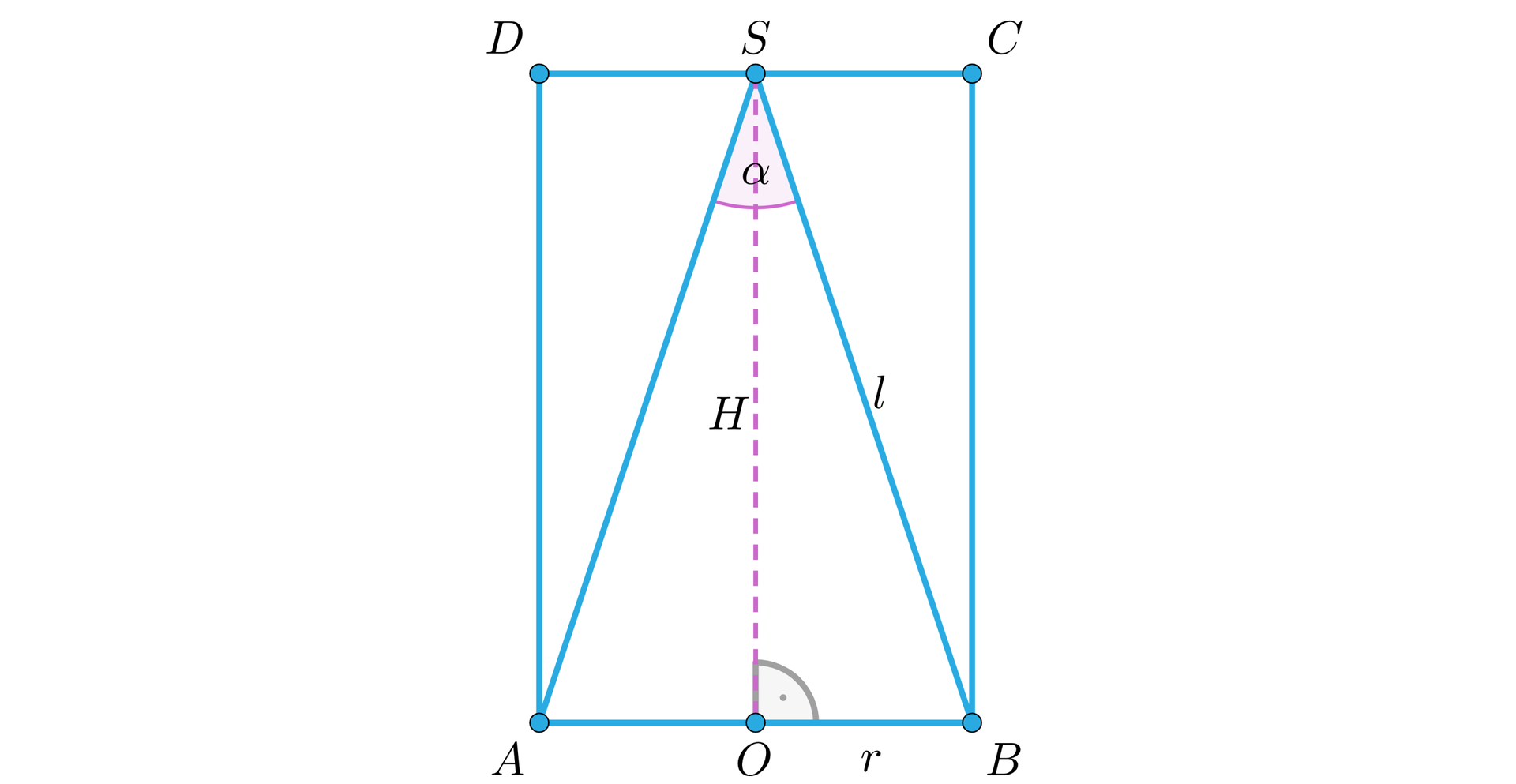
Przyjmujemy oznaczenia.
długość podstawy stożka i walca,
długość wysokości walca i stożka,
długość tworzącej stożka.
Kąt rozwarcia stożka, który mamy wyznaczyć to . Przyjmijmy, że .
Wyznaczymy miarę kąta rozwarcia stożka dwoma metodami.
metoda
Z warunków zadania otrzymujemy zależność , stąd mamy .
Zauważmy, że z twierdzenia Pitagorasatwierdzenia Pitagorasa, mamy , zatem , a stąd .
Określmy stosując twierdzenie cosinusówtwierdzenie cosinusów dla trójkąta . Mamy zatem . Podstawiając odpowiednio otrzymujemy zależność , stąd , zatem , stąd .
metoda
Przyjmijmy . W trójkącie prostokątnym mamy zależność .
Z warunków zadania otrzymujemy zależność , stąd mamy .
Zatem . Otrzymujemy , a stąd .
Kąt rozwarcia stożka jest kątem rozwartym o mierze .
Słownik
przekrój stożka płaszczyzną zawierającą oś obrotu stożka. Przekrój osiowy stożka jest trójkątem równoramiennym
przekrój walca płaszczyzną zawierającą oś obrotu walca. Przekrój osiowy walca jest prostokątem
w dowolnym trójkącie, kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi
jeśli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej
zależność opisująca cosinus miary kąta podwojonego