Przeczytaj

Zacznijmy od przypomnienia definicji i najważniejszych własności czworokąta wpisanego w okrąg.

Czworokąt wpisany w okrąg

Definicja: Czworokąt wpisany w okrąg

Czworokąt, którego wszystkie wierzchołki leżą na jednym okręgu.

Własności czworokąta wpisanego w okrąg

RxwmYSpqRZnJr

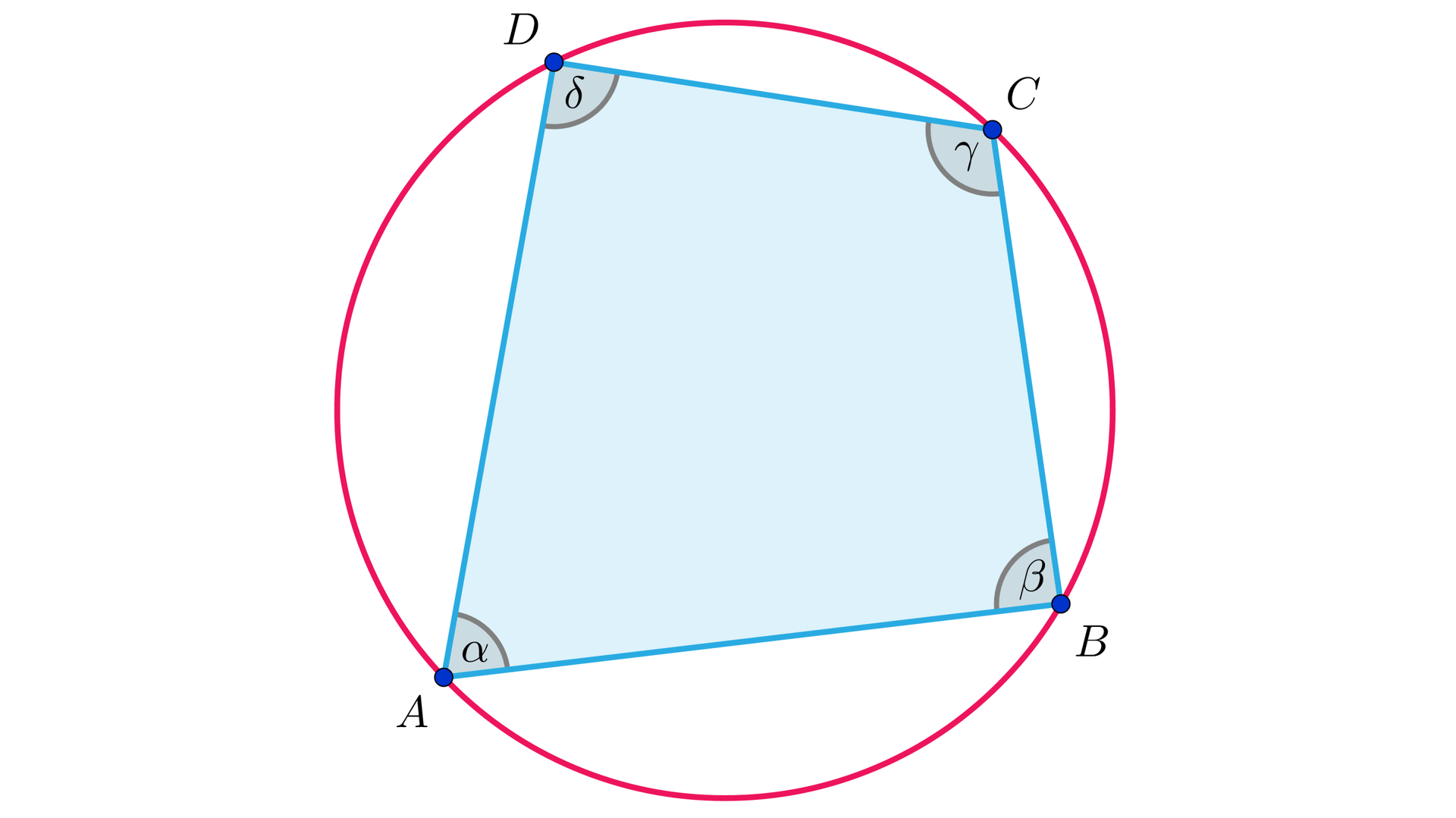
Ilustracja przedstawia czworokąt ABCD wpisany w okrąg. Kąt przy wierzchołku A ma miarę alfa, kąt przy wierzchołku B ma miarę beta, kąt przy wierzchołku C ma miarę gamma, a kąt przy wierzchołku D ma miarę delta.

Ważne!

Czworokąt wypukły można wpisać w okrąg wtedy i tylko wtedy, gdy suma jego przeciwległych kątów jest równa $180 °$ , czyli gdy

α + γ = β + δ = 180 °

Czworokąt można wpisać w okrąg wtedy i tylko wtedy, gdy symetralnesymetralna odcinkasymetralne wszystkich jego boków przecinają się w jednym punkcie.

Wniosek: TrapeztrapezTrapez można wpisać w okrąg wtedy i tylko wtedy, gdy jest równoramienny.

Powyższy fakt możemy udowodnić, korzystając z własności kątów w trapezie i w czworokącie wpisanym w okrąg. Wniosek ten wynika również z prostej obserwacji, że symetralna dowolnej cięciwy w okręgu jest prostopadła do niej i przechodzi przez środek tego okręgu. Zatem dwie równoległe cięciwy mają wspólną oś symetrii (jest nią ich symetralna). Zatem trapez o wierzchołkach w końcach tych cięciw jest równoramienny.

Dla zainteresowanych

Twierdzenie Ptolemeusza

Czworokąt $A B C D$ można opisać na okręgu wtedy i tylko wtedy, gdy iloczyn długości przekątnych równy jest sumie iloczynów długości przeciwległych boków.

Dla czworokątów wpisanych w okrąg zachodzi, przypominający nieco wzór Herona, wzór Brahmagupty:

S = \sqrt{(p - a) (p - b) (p - c) (p - d)}

gdzie $p = \frac{1}{2} (a + b + c + d)$ – połowa obwodu czworokąta, $a, b, c, d$ – długości boków czworokąta.

Poniżej kilka przykładów wyznaczania pole czworokąta wpisanego w okrąg.

Zacznijmy od prostego przykładu.

Przykład 1

Obliczymy pole czworokąta wpisanego w okrąg. Promień tego okręgu jest równy $5$ . Przekątne tego czworokąta są średnicami tego okręgu i przecinają się pod kątem $30 °$ .

Rozwiązanie

Aby rozwiązać to zadanie wystarczy, że zastosujemy wzór na pole czworokąta o danych przekątnych i kącie $α$ między nimi:

$P = \frac{1}{2} d_{1} \cdot d_{2} \cdot \sin α = \frac{1}{2} \cdot 10 \cdot 10 \cdot \frac{1}{2} = 25$ .

W powyższym przykładzie nie musieliśmy wykorzystywać faktu, że zadany czworokąt jest prostokątem (co wynika z faktu, że kąt oparty na średnicy jest kątem prostym).

Jednak w wielu zadaniach zanim zastosujemy odpowiedni wzór na pole czworokąta, będziemy musieli przeanalizować własności danego czworokąta.

Przykład 2

Trapez $A B C D$ wpisany jest w okrąg, przy czym dłuższa podstawa $A B$ trapezu o długości $20$ jest średnicą tego okręgu. Ramię $B C$ ma długość $10$ . Obliczymy pole tego trapezu.

R1aTnkveSHdHX

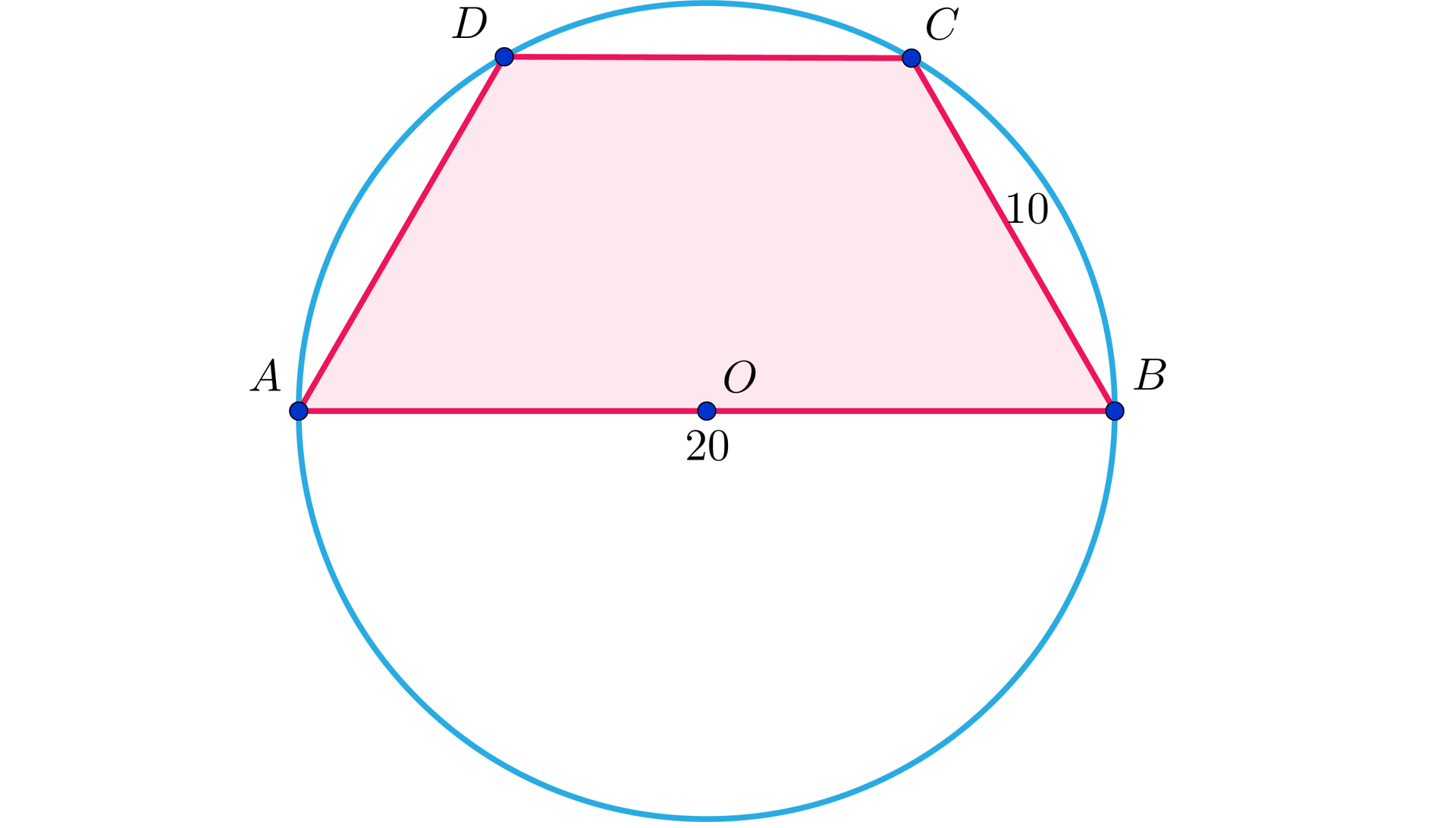
Ilustracja przedstawia trapez ABCD wpisany w okrąg. Dłuższa podstawa AB o boku 20 jest średnicą okręgu. Ramię BC ma długość 10 jednostek.

Rozwiązanie

Na początek przypomnijmy, że trapez wpisany w okrąg jest trapezem równoramiennym, zatem $|A D| = |B C| = 10$ . Ponadto promień okręgu też jest równy $10$ , więc możemy wywnioskować, że trójkąty $B O C$ i $A O D$ są trójkątami równobocznymi. Ich kąty przy wierzchołku $O$ mają miarę $60 °$ . Kąt $C O D$ również ma miarę $60 °$ . Wynika stąd, że trójkąt $O C D$ jest również równoboczny. Zatem pole trapezu jest równe sumie pól trzech trójkątów równobocznych o boku długości $10$ :

$S = 3 \cdot \frac{10^{2} \sqrt{3}}{4} = 75 \sqrt{3}$ .

Przeanalizujmy teraz ważne zadanie związane z wyznaczeniem pola czworokąta, gdy dane są długości jego boków. Rozwiążemy ten problem dwoma sposobami.

Przykład 3

Obliczymy pole czworokąta $A B C D$ wpisanego w okrąg. Długości boków tego czworokąta są równe: $|A B| = 2$ , $|B C| = 3$ , $|C D| = 4$ , $|D A| = 5$ .

Rozwiązanie

Zadanie to można rozwiązać błyskawicznie wyliczając wartość połowy obwodu

$p = \frac{1}{2} (2 + 3 + 4 + 5) = 7$

i podstawiając do wzoru Brahmagupty:

$S = \sqrt{(p - a) (p - b) (p - c) (p - d)}$ .

Zatem

$S = \sqrt{(7 - 2) (7 - 3) (7 - 4) (7 - 5)} = \sqrt{5 \cdot 4 \cdot 3 \cdot 2} = 2 \sqrt{30}$ .

Powyższego wzoru nie ma w tablicach matematycznych, rzadko też jest stosowany na lekcjach. Spróbujmy więc wyznaczyć to pole, odwołując się do wiadomości „szkolnych”. Powtórzymy przykład rozwiązując go inną metodą.

Przykład 4

Przypomnijmy, że szukamy pola czworokąta $A B C D$ wpisanego w okrąg. Długości boków tego czworokąta są równe: $|A B| = 2$ , $|B C| = 3$ , $|C D| = 4$ , $|D A| = 5$ .

Rozwiązanie

R1a0DQLl9QLkO

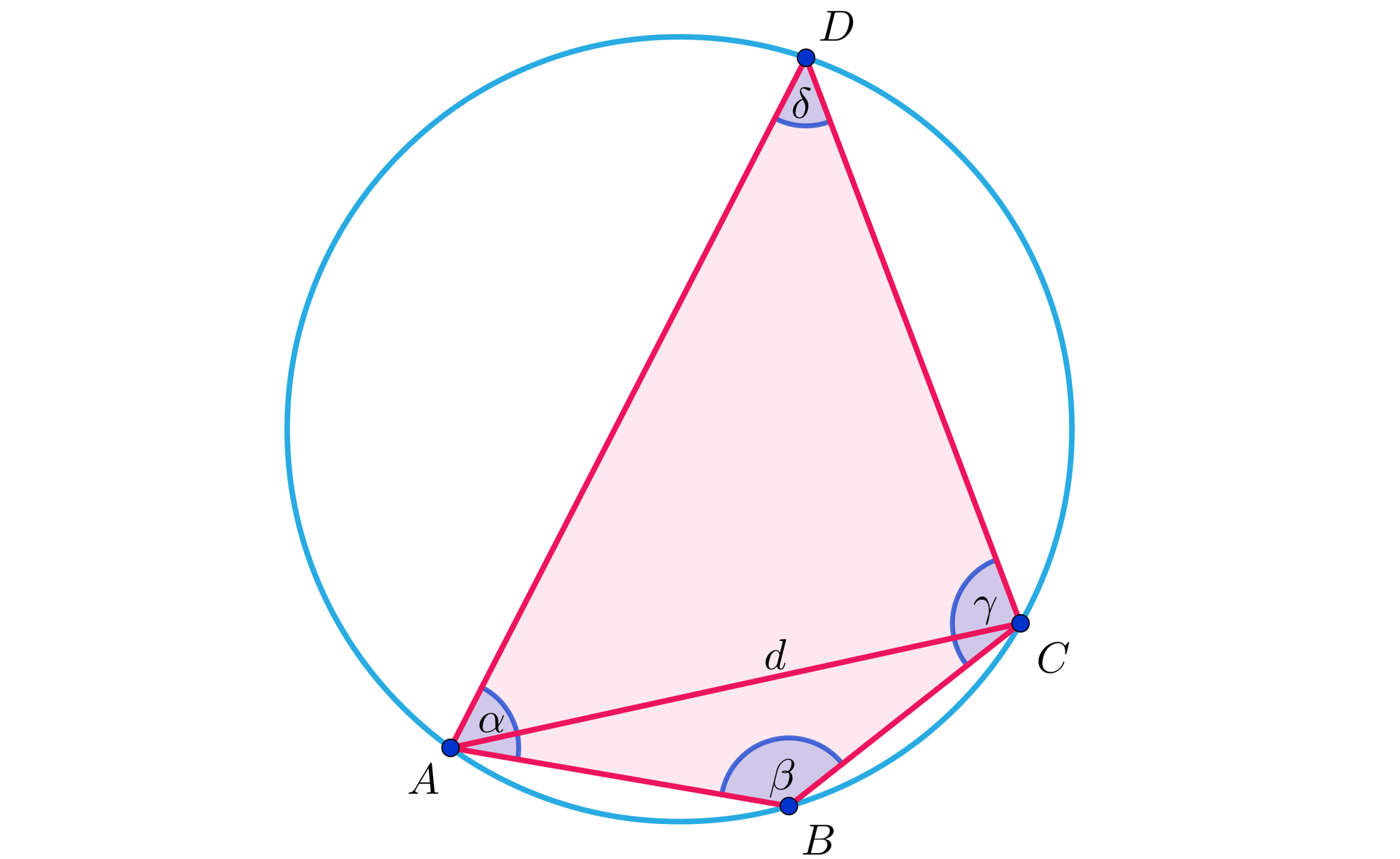
Ilustracja przedstawia czworokąt ABCD wpisany w okrąg o kątach wewnętrznych przy wierzchołku A alfa, B beta, C gamma i D delta. Zaznaczono przekątną AC.

Oznaczymy długość przekątnej $A C$ literą $d$ i zastosujemy twierdzenie cosinusów dla trójkątów $A B C$ i $A D C$ . Wykorzystamy fakt, że $δ = 180^{\circ} - β$ oraz $\cos (180 ° - β) = - \cos β$ .

Otrzymujemy dwa równania:

$d^{2} = 4 + 9 - 12 \cos β$ ,

$d^{2} = 16 + 25 + 40 \cos β$ .

Porównując prawe strony otrzymujemy:

$4 + 9 - 12 \cos β = 16 + 25 + 40 \cos β$ ,

$52 \cos β = - 28$ ,

$\cos β = - \frac{7}{13}$ .

Następnie korzystamy z jedynki trygonometrycznej:

$\sin β = \sqrt{1 - {(\cos β)}^{2}} = \sqrt{1 - \frac{49}{169}} = \sqrt{\frac{120}{169}} = \frac{2}{13} \sqrt{30}$ .

Szukane pole czworokąta $A B C D$ jest sumą pól trójkątów $A B C$ i $A C D$ , więc wykorzystując wzór na pole trójkąta otrzymujemy:

$S = \frac{1}{2} \cdot |A B| \cdot |B C| \cdot \sin β + \frac{1}{2} \cdot |A D| \cdot |D C| \cdot \sin (180 ° - β) =$

$= \frac{1}{2} \cdot 2 \cdot 3 \cdot \frac{2}{13} \sqrt{30} + \frac{1}{2} \cdot 4 \cdot 5 \cdot \frac{2}{13} \sqrt{30} = \frac{26}{13} \sqrt{30} = 2 \sqrt{30}$ .

Ciekawostka

Przy okazji dwóch powyższych rozwiązań warto zauważyć, że postępując podobnie jak w przykładzie 3, możemy wyprowadzić wzór na pole czworokąta wpisanego w okrąg o danych długościach boków, więc wzór Brahmagupty.

Nieco bardziej skomplikowane jest wyprowadzenie wzoru na pole dowolnego czworokąta o danych długościach boków. Postępuje się podobnie, choć potrzebna jest nam wtedy dodatkowa informacja o czworokącie (np. kąt lub przekątna).

Okazuje się, że spośród wszystkich czworokątów o zadanych długościach kolejnych boków, największe pole ma ten wpisany w okrąg!

Przykład 5

Trapez równoramienny wpisany jest w okrąg o promieniu $5$ , przy czym dłuższa podstawa ma długość $8$ , a krótsza $6$ . Zastanówmy się jakie może być pole tego trapezu.

Rozwiązanie

Polecenie „jakie może być pole trapezu” sugeruje, że odpowiedź nie musi być jednoznaczna. W zadaniu mamy okrąg o promieniu $5$ i dwie równoległe cięciwy (będące podstawami trapezu). Możliwe są zatem dwie opcje (rysunek):

RIsqh5kCztj3v

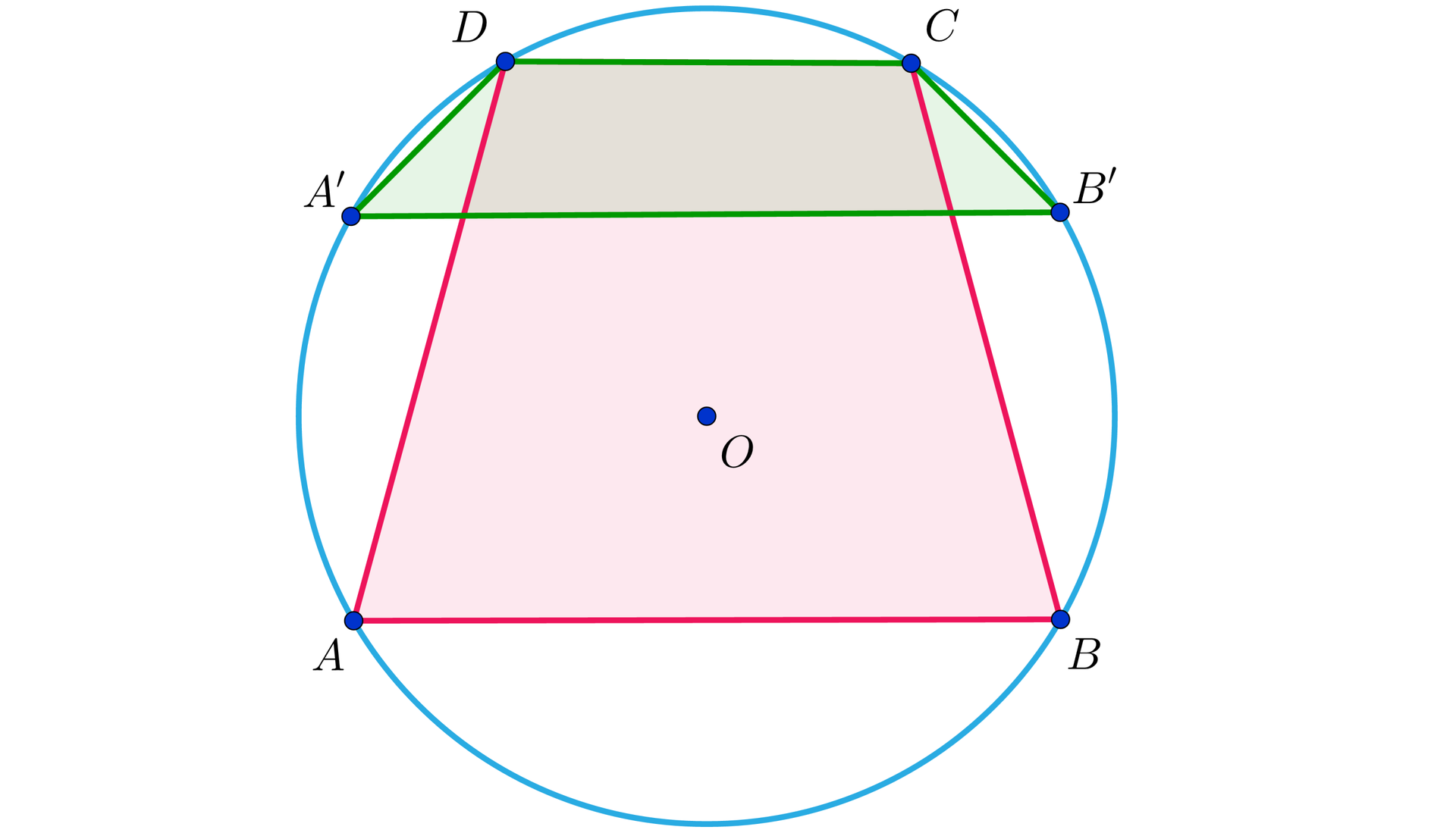
Ilustracja przedstawia czworokąty ABCD i A prim B prim CD wpisane w okrąg. Czworokąty posiadają wspólną podstawę DC.

Wyznaczymy wysokości tych trapezów, czyli odległości podstaw. Zauważmy że można to zrobić wyznaczając odległość środka okręgu od dłuższej podstawy ( $h_{1}$ ) oraz od krótszej podstawy ( $h_{2}$ ). Trapez o większym polu będzie miał wysokość równą sumie tych odległości, natomiast trapez o mniejszym polu będzie miał wysokość równą różnicy tych odległości.

R1ZSeFjd3JH4h

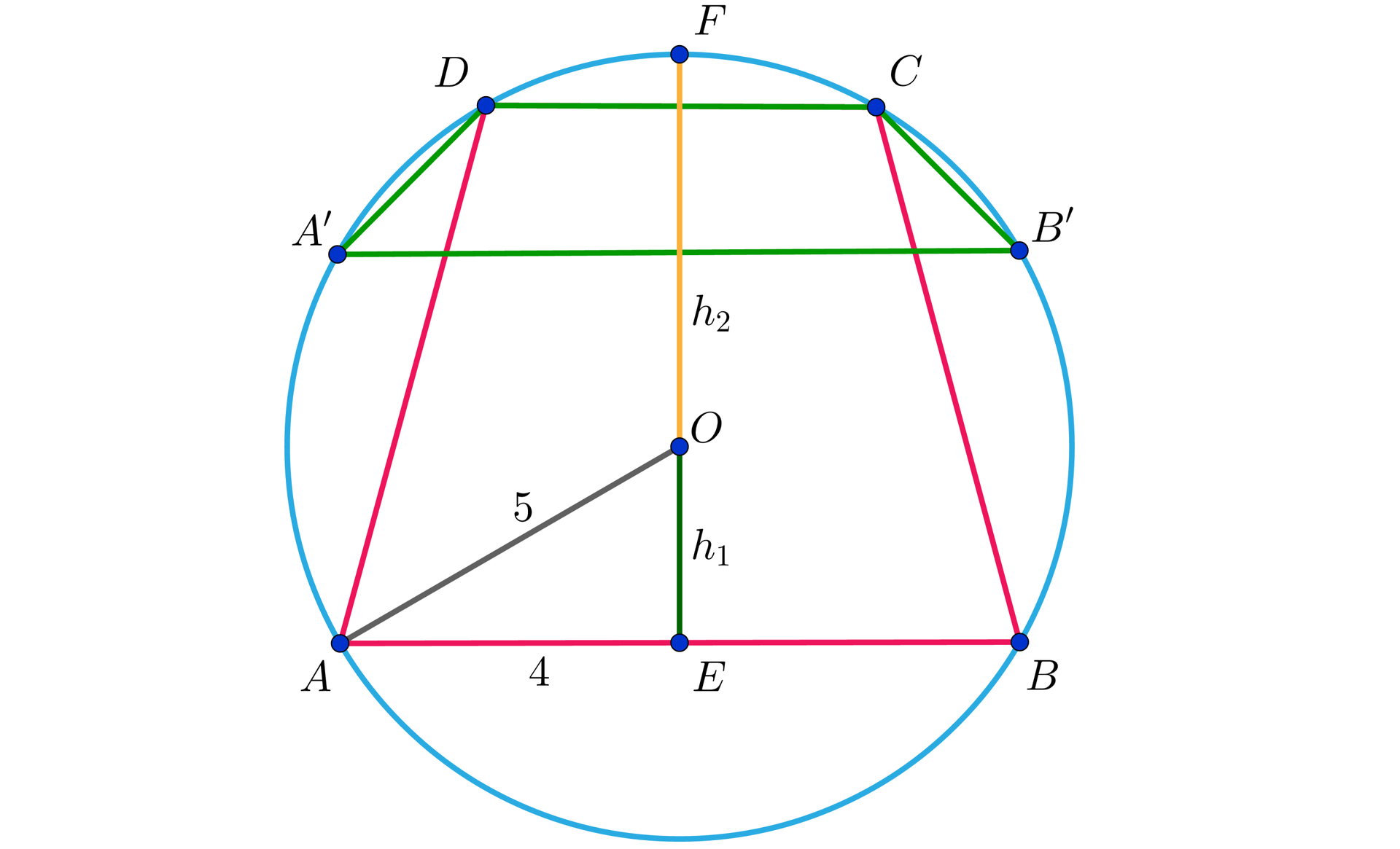
Ilustracja przedstawia czworokąty ABCD i A prim B prim CD wpisane w okrąg. Czworokąty posiadają wspólną podstawę DC. Zaznaczono wysokość FE. Punkt E znajduję się na środku boku AB dzieląc go na połowę równą cztery. Punkt E połączono z punktem O, a punkt A połączono z punktem O tworząc trójkąt prostokątny AOE o przyprostokątnych 4 i h indeks dolny 1 koniec indeksu oraz przeciwprostokątnej pięć.

Wartości $h_{1}$ oraz $h_{2}$ obliczamy z twierdzenia Pitagorasa:

${h_{1}}^{2} + 4^{2} = 5^{2} \Rightarrow h_{1} = 3$

${h_{2}}^{2} + 3^{2} = 5^{2} \Rightarrow h_{2} = 4$

Zatem szukane pole ma wartość:

$S = \frac{1}{2} (8 + 6) (3 + 4) = 49$

lub

$S = \frac{1}{2} (8 + 6) (4 - 3) = 7$ .

Słownik

trapez

czworokąt (wypukły) mający przynajmniej jedną parę równoległych boków; (wybraną) parę boków równoległych nazywa się podstawami, pozostałe boki noszą nazwę ramion, odległość między podstawami nazywa się wysokością trapezu

symetralna odcinka

prosta prostopadła do danego odcinka przechodząca przez jego środek; równoważnie – prosta będąca zbiorem punktów równo oddalonych od obu końców odcinka

Wprowadzenie

Symulacja interaktywna

Własności czworokąta wpisanego w okrąg

Słownik