Przeczytaj
Najważniejszymi odcinkami w walcu są: wysokość, promień podstawy, średnica podstawy i przekątna przekroju osiowegoprzekroju osiowego.
Przypomnijmy, że przekrój osiowy walca jest prostokątem o wymiarach . Przekątna przekroju osiowego ma więc długość .
Na rysunku poniżej zaznaczono kąt pomiędzy przekątną przekroju osiowego, a promieniem (średnicą) podstawy.

Trójkąt, którego bokami są średnica podstawy, wysokość walca i przekątna przekroju osiowego jest trójkątem prostokątnym.
Obliczymy miarę kąta nachylenia przekątnej przekroju osiowego walca do średnicy podstawy, jeżeli wysokość walca jest dwukrotnie dłuższa od promienia podstawy.
Rozwiązanie:
Jeżeli wysokość jest dwukrotnie dłuższa od promienia podstawy, to znaczy, że średnica ma długość równą długości wysokości. A zatem trójkąt prostokątny, którego bokami są średnica, wysokość i przekątna jest równoramienny. Szukany kąt ma więc miarę .
Kąt pomiędzy przekątną przekroju osiowego, a średnicą podstawy walca ma miarę . Obliczymy objętość i pole powierzchni tego walca, jeżeli wysokość tego walca wynosi .
Rozwiązanie:
Zróbmy rysunek pomocniczy:

Mamy, że
Czyli , a stąd .
Mamy więc oraz .
Wysokość walca, która zawiera się w jego powierzchni bocznej, nazywamy tworzącą walca. Na rysunku poniżej zaznaczony został kąt pomiędzy przekątną przekroju osiowego, a tworzącą walca.

Przekątna przekroju osiowego walca ma długość , a promień . Obliczymy tangens kąta pomiędzy przekątną tego przekroju a tworzącą.
Rozwiązanie:
Zróbmy rysunek pomocniczy:

Obliczymy z z twierdzenia Pitagorasa: , a stąd . A zatem .
Suma miar kątów pomiędzy przekątną przekroju osiowego, a promieniem podstawy oraz pomiędzy przekątną przekroju osiowego, a tworzącą wynosi .
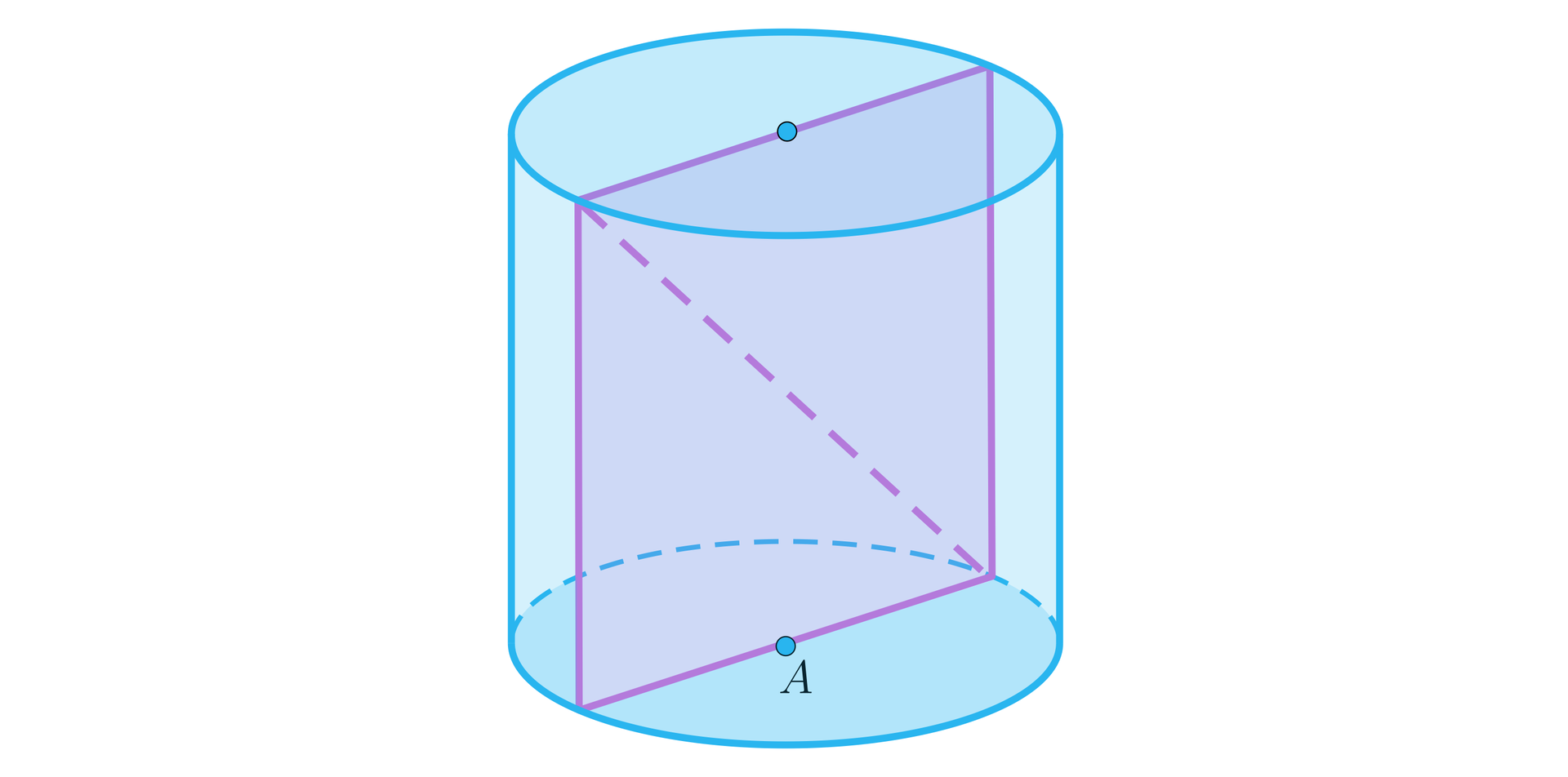
Kąt pomiędzy przekątnymi pewnego przekrojuprzekroju walca, prostopadłego do podstawy i odległego od środka o , ma miarę . Obliczymy pole tego przekroju wiedząc, że promień walca ma długość , a wysokość walca jest krótsza od boku przekroju zawartego w podstawie.
Rozpatrzmy teraz przekrój walca prostopadły do podstawy, różny od przekroju osiowego. Przekrój ten również ma kształt prostokąta.
Rozwiązanie:
Zróbmy rysunek pomocniczy:
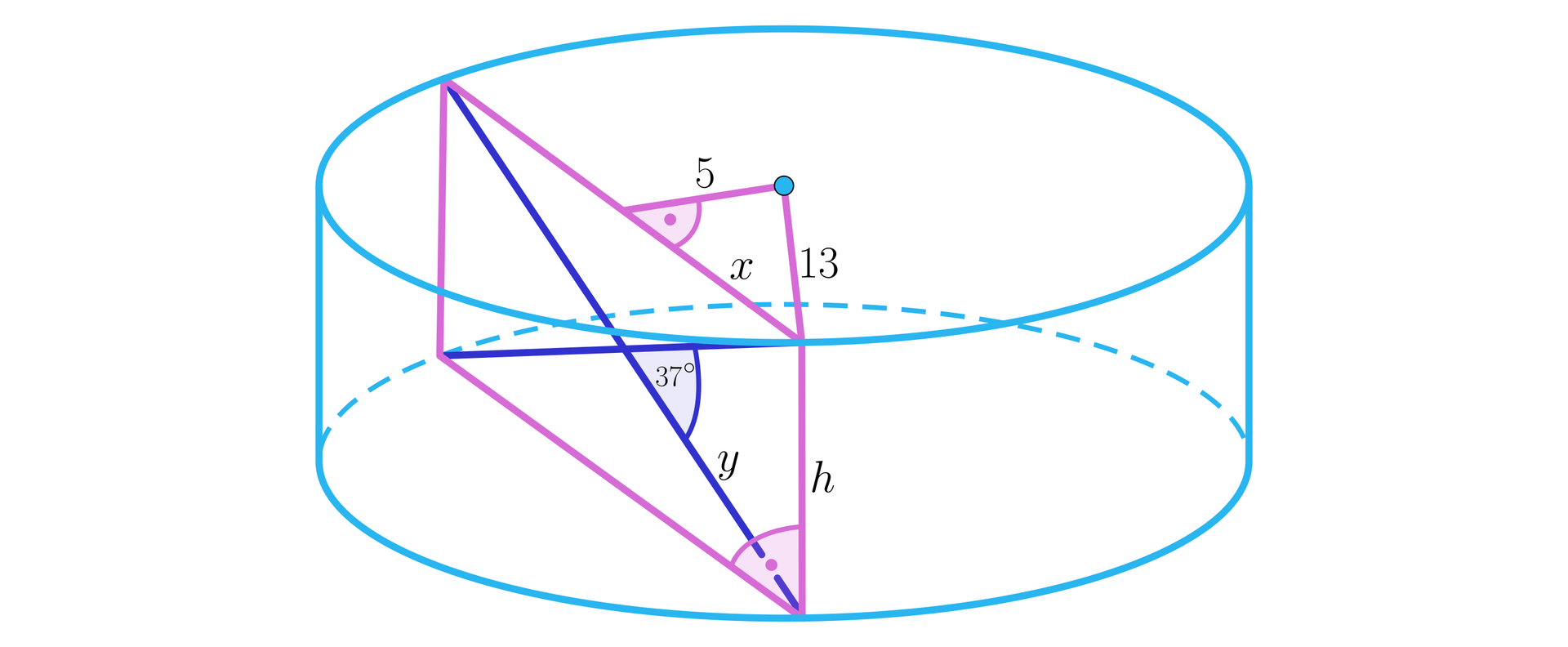
Obliczymy długość boku przekroju zawartego w podstawie walca:
Korzystamy z twierdzenia Pitagorasa: . A zatem .
Stąd bok przekroju zawarty w podstawie ma długość .
Obliczymy długość przekątnych tego przekroju z twierdzenia cosinusów:
A stąd , a zatem . Cała przekątna ma więc długość około .
Pole przekroju możemy obliczyć ze wzoru , gdzie jest długością przekątnej, a miarą kąta pomiędzy przekątnymi. Mamy więc .
Łącząc każdy z punktów na okręgu podstawy walca ze środkiem drugiej podstawy otrzymujemy odcinki, które są tworzącymi stożka o tej samej wysokości i tym samym promieniu co walec.

Mówimy wtedy, że stożek jest wpisany w walec.
Dany jest walec o promieniu i wysokości . W walcu tym poprowadzono przekrój osiowy. Obliczymy miarę kąta pomiędzy odcinkami łączącymi wierzchołki dłuższego boku przekroju ze środkiem drugiej podstawy. Odpowiemy na pytanie, czym ten kąt jest dla stożka powstałego przez połączenie punktów na brzegu podstawy ze środkiem drugiej podstawy.
Rozwiązanie:
Zróbmy rysunek pomocniczy:

Z twierdzenia Pitagorasa otrzymujemy, że odcinek ma długość . Obliczymy miarę kąta z twierdzenia cosinusów:
A zatem . Stąd .
Dla stożka wpisanego w walec kąt ten jest kątem rozwarcia stożka.
Słownik
figura geometryczna będąca częścią wspólną bryły i płaszczyzny, która ją przecina
przekrój bryły obrotowej zawierający oś obrotu