Przeczytaj

Rozpoczniemy lekcję od wykreślenia wykresu funkcji $y = \sin x$ .

Konstrukcja wykresu funkcji $y = \sin x$ w przedziale $⟨0, \frac{π}{2}⟩$ .

Zaznaczmy w układzie współrzędnych okrąg o promieniu $1$ . Niech będzie to okrąg o równaniu ${(x + 2)}^{2} + y^{2} = 1$ . Jego środkiem jest punkt $C (- 2, 0)$ . Niech punkt $D$ ma współrzędne $(- 1, 0)$ . Jeżeli przez leżący na danym okręgu punkt $A$ poprowadzimy prostą prostopadłą do osi $X$ , to przetnie ona tę oś w punkcie $E$ . Niech $a$ oznacza miarę kąta $D C A$ mierzoną w radianachradianradianach.

Punkt $B$ ma współrzędne $(a, \sin a)$ . Prosta przechodząca przez punkt $B$ i prostopadła do osi $X$ przecina tę oś w punkcie $F (a, 0)$ .

Otwórzmy aplet, aby obserwować całą konstrukcję.

R1Ty114AHox41

Zauważamy, że druga współrzędna punktu $A$ to $\sin a$ . Zatem odcinki $A E$ i $B F$ mają tę samą długość równą $\sin a$ . Punkt $B$ ma współrzędne $(a, \sin a)$ . Wobec tego punkt $B$ leży na wykresie funkcji $y = \sin a$ . Poruszający się punkt $B$ wyznacza wykres funkcji $y = \sin a$ .

Zastosowaliśmy miarę kąta z przedziału $⟨0, \frac{π}{2}⟩$ . Zatem w tym przedziale otrzymaliśmy wykres funkcji $y = \sin a$ .

Konstrukcja wykresu funkcji $y = \sin x$ w przedziale $⟨\frac{π}{2}, π⟩$ .

Teraz skonstruujemy wykres $y = \sin a$ dla $a \in ⟨\frac{π}{2}, π⟩$ . W tym celu wykorzystamy wzór redukcyjny: $\sin (π - a) = \sin a$ dla dowolnej liczby rzeczywistej $a$ .

Wzór redukcyjny $\sin (π - a) = \sin a$ opisuje własność: osią symetrii wykresuoś symetrii wykresuosią symetrii wykresu funkcji $y = \sin a$ jest prosta o równaniu $x = \frac{π}{2}$ . Dlaczego tak się dzieje?

Rc3gNM13VZIAa

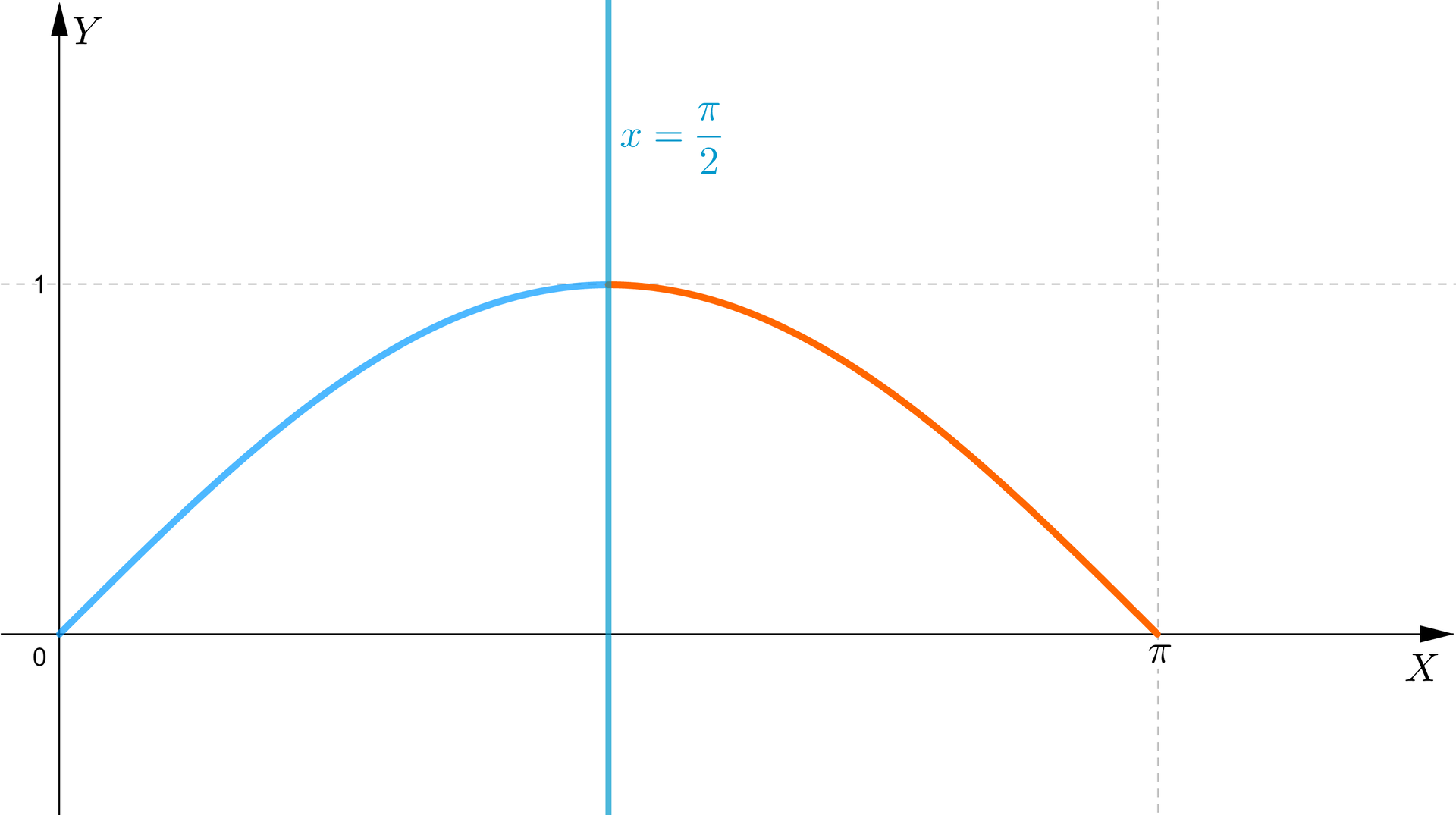
Na rysunku przedstawiony jest układ współrzędnych, oś pozioma widoczna jest w przedziale 0;π. Zaznaczono na nim fragment wykresu sinus. Wykres ma pagórkowaty kształt. Zaczyna się w początku układu współrzędnych, biegnie do swojego maksimum w punkcie π2;1. Dalej wartości funkcji maleją aż osiągną miejsce zerowe o współrzędnych π;0. Przy maksimum wykres jest zaokrąglony. Na płaszczyźnie narysowano także pionową prostą o x=π2, która dzieli fragment wykresu funkcji sinus na pół. Obie części wykresu funkcji sinus są do siebie symetryczne względem pionowej osi.

Ważne!

Jeżeli dane dwa punkty $P (x_{1}, y_{1})$ i $Q (x_{2}, y_{2})$ są symetryczne względem prostej $k$ o równaniu $x = b$ , to ich drugie współrzędne $y_{1}$ i $y_{2}$ są równe. Środek odcinka $P Q$ znajduje się na prostej $k$ . Zatem $\frac{x_{1} + x_{2}}{2} = b$ , czyli $x_{2} = 2 b - x_{1}$ .

Otrzymaliśmy wykres funkcji $y = \sin a$ w przedziale $⟨0, π⟩$ .

Konstrukcja wykresu funkcji $y = \sin a$ w przedziale $⟨- π, π⟩$ .

Skorzystamy z kolejnego wzoru charakterystycznego dla funkcji sinus: dla każdej liczby rzeczywistej $a$ zachodzi równość: $\sin (- a) = - \sin a$ . Własność ta oznacza, że wykres funkcji $y = \sin x$ jest symetrycznyśrodek symetrii wykresusymetryczny względem początku układu współrzędnych. Oznacza to także, że funkcja sinus jest funkcją nieparzystą.

RNjVF0MoQ5dK1

Ilustracja przedstawia układ współrzędnych, pozioma oś X zaznaczona w przedziale -π;π. Zaznaczono na nim funkcje sinus. Miejsca zerowe funkcji to -π, 0 oraz π. Rysunek przedstawia pełny cykl czy też przebieg funkcji.

Zatem otrzymaliśmy wykres $y = \sin a$ w przedziale $⟨- π, π⟩$ .

Konstrukcja wykresu funkcji $y = \sin a$ w zbiorze liczb rzeczywistych.

Aby skonstruować wykres funkcji $y = \sin x$ dla $x \in ℝ$ , skorzystamy z kolejnej własności funkcji sinus: $\sin (a + 2 π) = \sin a$ , dla każdej liczby $a \in ℝ$ . Własność ta oznacza, że wykres funkcji sinus przesunięty o $(- 2 π)$ jest tym samym wykresem. Zatem funkcja sinus jest funkcją okresową o okresie $T = 2 k π$ , gdzie $k \in ℤ$ i $k \neq 0$ .

Przykład 1

Opiszmy własności funkcji $y = \sin x$ , gdy $x \in ℝ$ .

Funkcja sinus jest funkcją okresową o okresie zasadniczym $T = 2 π$ .
Funkcja sinus jest funkcją nieparzystą.
Zbiorem wartości jest przedział $⟨- 1, 1⟩$ .
Wartość największą równą 1 funkcja osiąga dla argumentów: $x = \frac{π}{2} + 2 k π$ , gdzie $k \in ℤ$ .
Wartość najmniejszą równą -1 funkcja osiąga dla argumentów: $x = - \frac{π}{2} + 2 k π$ , gdzie $k \in ℤ$ .
Miejscami zerowymi są argumenty: $x = k π$ , gdzie $k \in ℤ$ .
Funkcja jest rosnąca w przedziałach: $⟨- \frac{π}{2} + 2 k π, \frac{π}{2} + 2 k π⟩$ , gdzie $k \in ℤ$ .
Funkcja jest malejąca w przedziałach: $⟨\frac{π}{2} + 2 k π, \frac{3 π}{2} + 2 k π⟩$ , gdzie $k \in ℤ$ .

Przykład 2

Opiszmy własności geometryczne wykresu funkcji $y = \sin x$ , gdy $x \in ℝ$ .

Osią symetriioś symetrii wykresuOsią symetrii wykresu jest każda prosta o równaniu $x = \frac{π}{2} + k π$ , gdzie $k \in ℤ$ .
Środkiem symetriiśrodek symetrii wykresuŚrodkiem symetrii wykresu jest każdy punkt o współrzędnych $(k π, 0)$ , gdzie $k \in ℤ$ .

Przykład 3

Podamy okres zasadniczy każdej z poniższych funkcji.

Funkcja $y = 2 \sin x$ ma okres zasadniczy $T = 2 π$ , gdyż $2 \sin (x + 2 π) = 2 \sin x$ .
Funkcja $y = \sin (2 x)$ ma okres zasadniczy $T = π$ , gdyż $\sin 2 (π + x) = \sin (2 π + 2 x) = \sin (2 x)$ .
Funkcja $y = |\sin x|$ ma okres zasadniczy $T = π$ , gdyż $|\sin (π + x)| = |- \sin x| = |\sin x|$ .

Przykład 4

Która wartość jest większa: $\sin \frac{π}{7}$ czy $\sin \frac{4 π}{27}$ ?

Zauważmy, że $\frac{π}{7} \in ⟨0, \frac{π}{2}⟩$ i $\frac{4 π}{27} \in ⟨0, \frac{π}{2}⟩$ .

Zauważmy także, że $\frac{π}{7} < \frac{4 π}{27}$ . Ponieważ funkcja sinus w tym przedziale jest rosnąca, zachodzi zatem nierówność: $\sin \frac{π}{7}$ < $\sin \frac{π}{7} < \sin \frac{4 π}{27}$ .

Słownik

oś symetrii wykresu

prosta $k$ jest osią symetrii wykresu funkcji $f$ wtedy, gdy obrazem wykresu funkcji $f$ w symetrii osiowej względm prostej $k$ jest ten sam wykres

radian

jednostka miary łukowej kąta środkowego $α$ wyrażająca stosunek długości łuku, na którym oparty jest ten kąt, do długości promienia okręgu, dla którego kąt $α$ jest kątem środkowym; związek pomiędzy miarą stopniową a łukową wyraża się wzorem

α [°] = \frac{α \cdot π}{180} = [radian]

środek symetrii wykresu

punkt $A$ jest środkiem symetrii wykresu funkcji $f$ wtedy, gdy obrazem wykresu funkcji $f$ w symetrii środkowej względm punktu $A$ jest ten sam wykres

Wprowadzenie

Symulacja interaktywna

Słownik