Przeczytaj

Wiemy już, że prostopadłościanprostopadłościanprostopadłościan to bryła przestrzenna posiadająca cztery prostokątne ściany boczne oraz prostokąty w podstawach.

Prostopadłościan składa się z:

$12$ krawędzi,
$8$ wierzchołków,
$6$ ścian.

Możemy powiedzieć, że prostopadłościan to równoległościan, w którym każde dwie ściany mające wspólną krawędź są prostopadłe.

Dla ułatwienia, przypomnijmy elementy budowy prostopadłościanu, analizując poniższą ilustrację.

RvGBFP17mOlPz

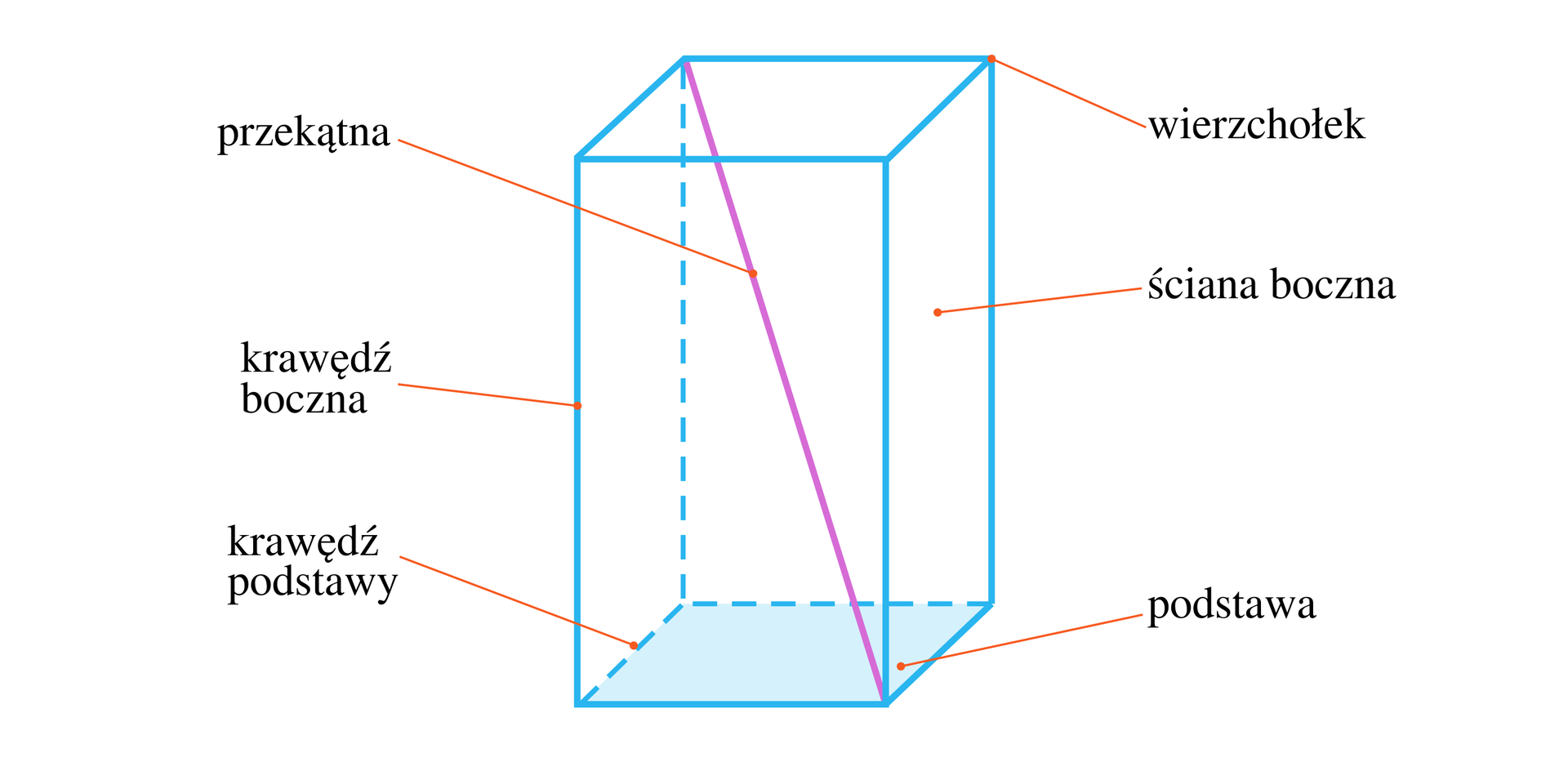
Na ilustracji przedstawiono prostopadłościan o dolnej podstawie A B C D oraz górnej E F G H. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F, nad wierzchołkiem C, wierzchołek G, oraz nad wierzchołkiem D wierzchołek H. Zaznaczono przekątną łączącą wierzchołek B z wierzchołkiem G, krawędź boczną A E, krawędź A C podstawy, jedną ze ścian bocznych, wierzchołek H, oraz wskazano dolną podstawę.

Długości odcinków w prostopadłościanie

Analizując budowę prostopadłościanu możemy zauważyć, że krawędzie boczne oraz krawędzie podstawy to nie jedyne odcinki, jakie znajdziemy w prostopadłościanie. Często niewiadomymi pozostają długości przekątnych ścian bocznych, przekątne podstawy, czy nawet przekątne prostopadłościanu.

Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.

R17I5Gb9FQBwQ

Na ilustracji przedstawiono sześcian o dolnej podstawie A B C D, oraz górnej E F G H. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F, nad wierzchołkiem C, wierzchołek G, oraz nad wierzchołkiem D wierzchołek H. Długości odcinków w prostopadłościanie oznaczono małymi literami alfabetu od a do f oraz x. Literą a oznaczono krawędź A B podstawy, literą b oznaczono krawędź B C podstawy, literą c oznaczono krawędź A E, literą d przekątną H B prostopadłościanu, literą e przekątną B G ściany bocznej, literą f oznaczono przekątną A F ściany bocznej, oraz literą x oznaczono przekątną B D podstawy.

Długość przekątnej ściany bocznej prostopadłościanu.

W prostopadłościanie mamy dwie pary ścian bocznych o różnych wymiarach. Zatem długości ich przekątnych obliczymy, korzystając z dwóch trójkątów prostokątnych.

Ry0OnjaxcwknO

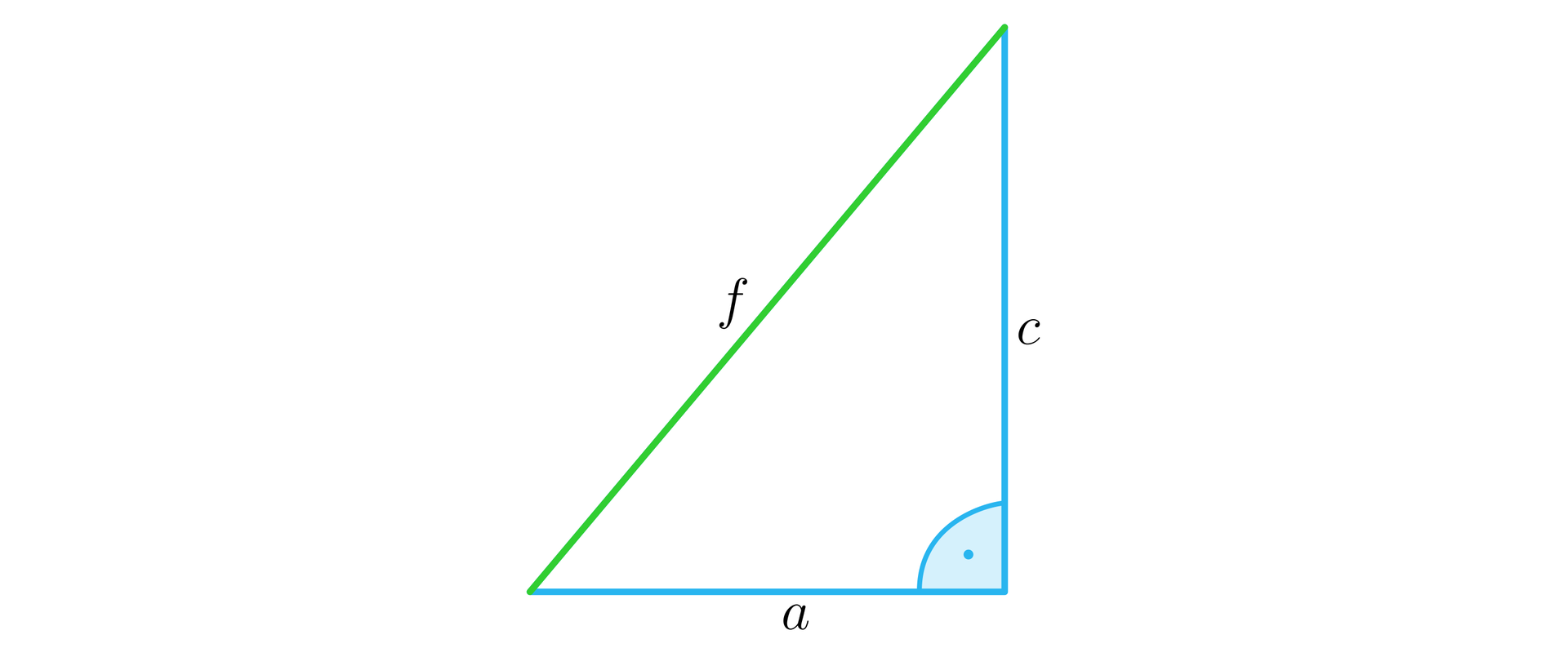
Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych a i c, oraz przeciwprostokątnej f.

Korzystając z twierdzenia Pitagorasa, mamy zależność $f^{2} = a^{2} + c^{2}$ , wobec tego

$f = \sqrt{a^{2} + c^{2}}$

R1MkGHvTWZKIg

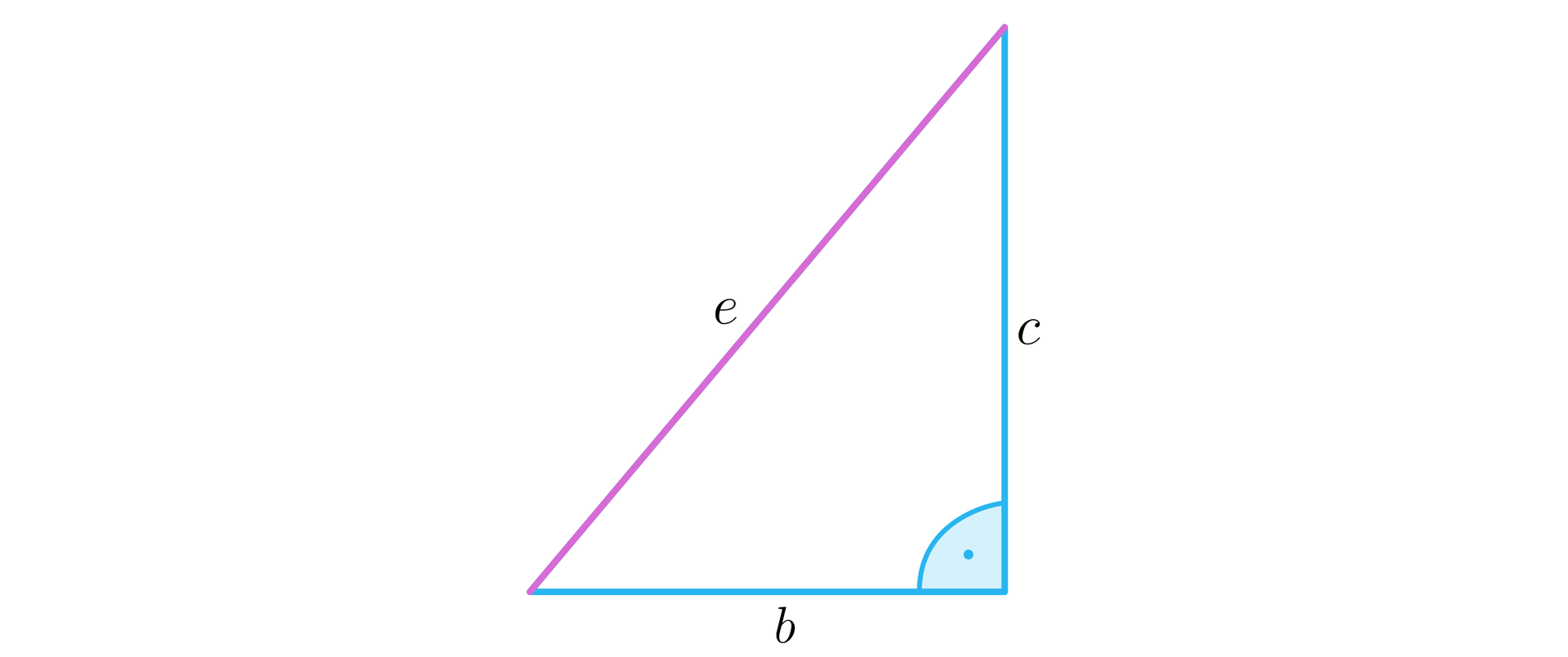
Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych b i c, oraz przeciwprostokątnej e.

Korzystając z twierdzenia Pitagorasa, mamy zależność $e^{2} = b^{2} + c^{2}$ , wobec tego

$e = \sqrt{b^{2} + c^{2}}$

Długość przekątnej podstawy prostopadłościanu.

RJCBmBC3MWHWP

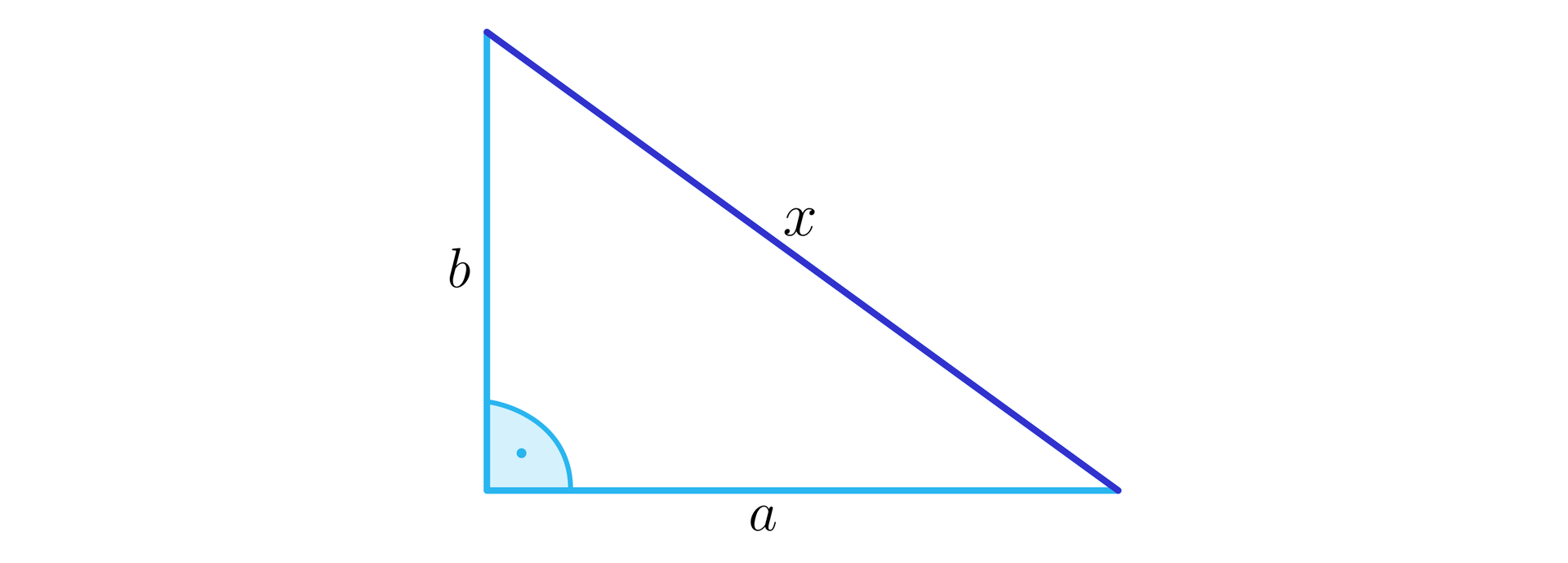
Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych a i b, oraz przeciwprostokątnej x.

Korzystając z twierdzenia Pitagorasa, otrzymujemy zależność $x^{2} = a^{2} + b^{2}$ , więc długość przekątnej podstawy prostopadłościanu $x$ obliczamy ze wzoru

$x = \sqrt{a^{2} + b^{2}}$

Długość przekątnej prostopadłościanu.

Zauważmy, że długość przekątnej $d$ możemy obliczyć, korzystając z twierdzenia Pitagorasa w poniższym trójkącie.

R1ZMZMz0wFPly

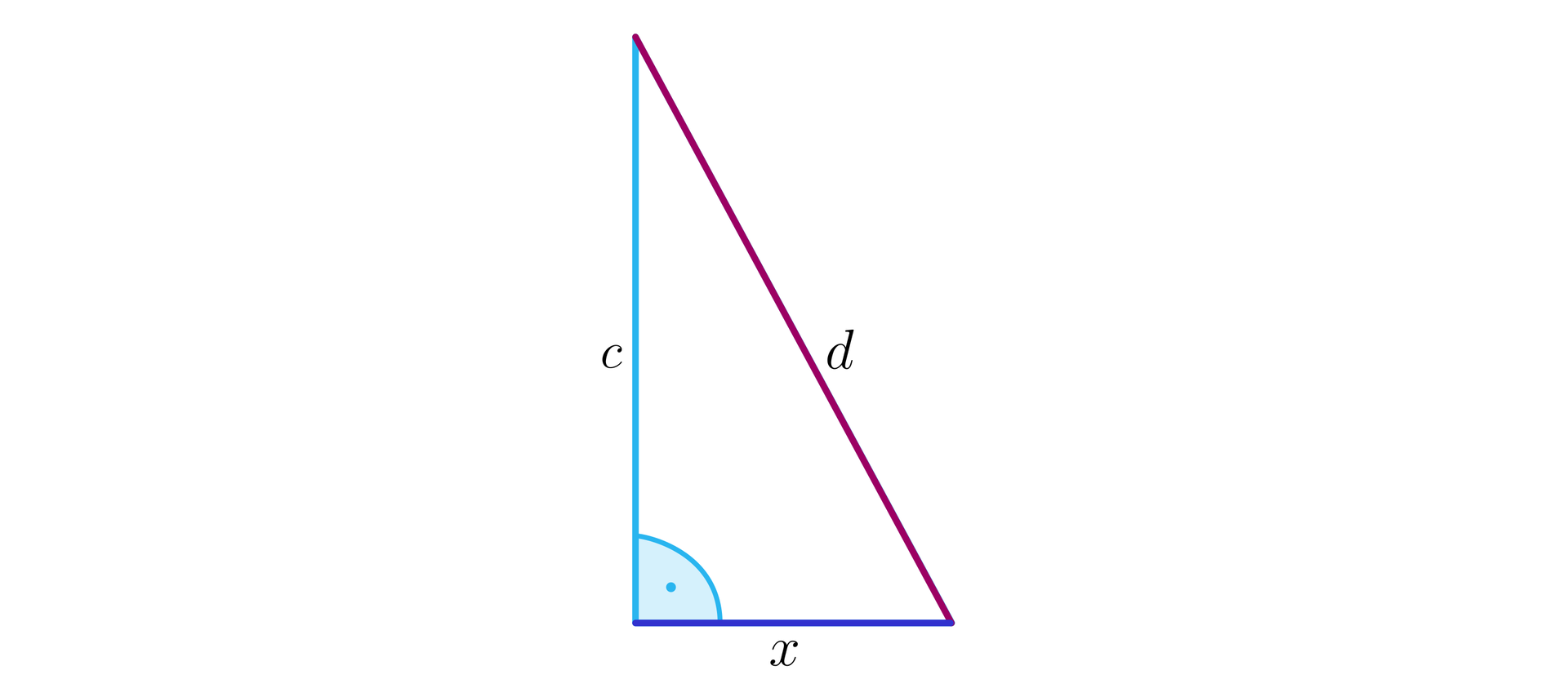
Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych c i x, oraz przeciwprostokątnej d.

Zatem:

x^{2} + c^{2} = d^{2}

Ponieważ zachodzi zależność

a^{2} + b^{2} = x^{2}

wobec tego

a^{2} + b^{2} + c^{2} = d^{2}

Jeżeli krawędzie prostopadłościanu mają długości $a$ , $b$ , $c$ , to długość przekątnej prostopadłościanu obliczamy ze wzoru:

d = \sqrt{a^{2} + b^{2} + c^{2}}

W prostopadłościanie możemy wyznaczyć także długości innych odcinków np.:

długość odcinka łączącego środki sąsiednich krawędzi w podstawie prostopadłościanu,
Rt3Ty5BCgZA6t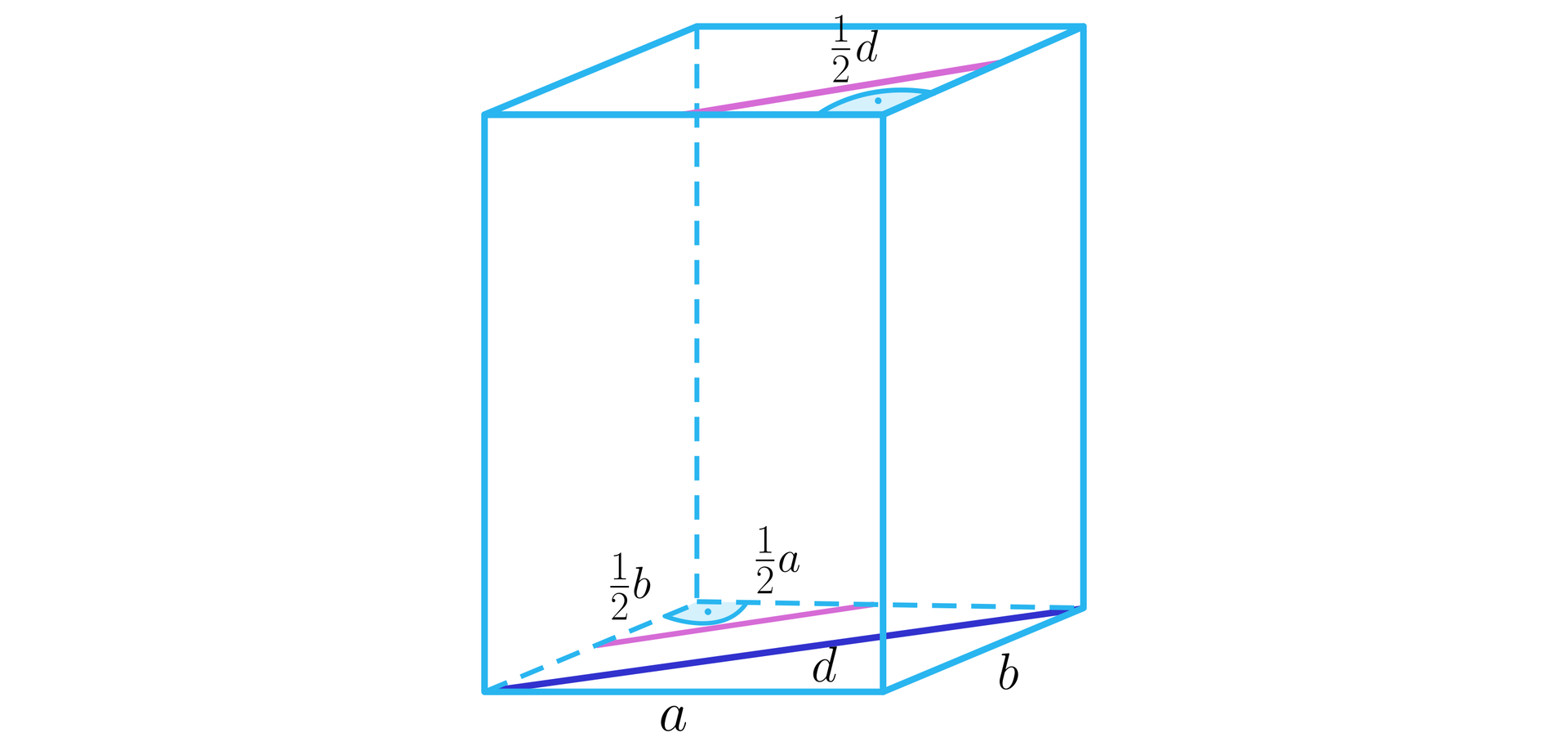
czyli długość odcinka łączącego środki sąsiednich krawędzi w podstawie prostopadłościanu jest równa połowie długości przekątnej tej podstawy;
długość odcinka łączącego środki przekątnych sąsiednich ścian bocznych w prostopadłościanie,
R1VUDGx1aCQ7g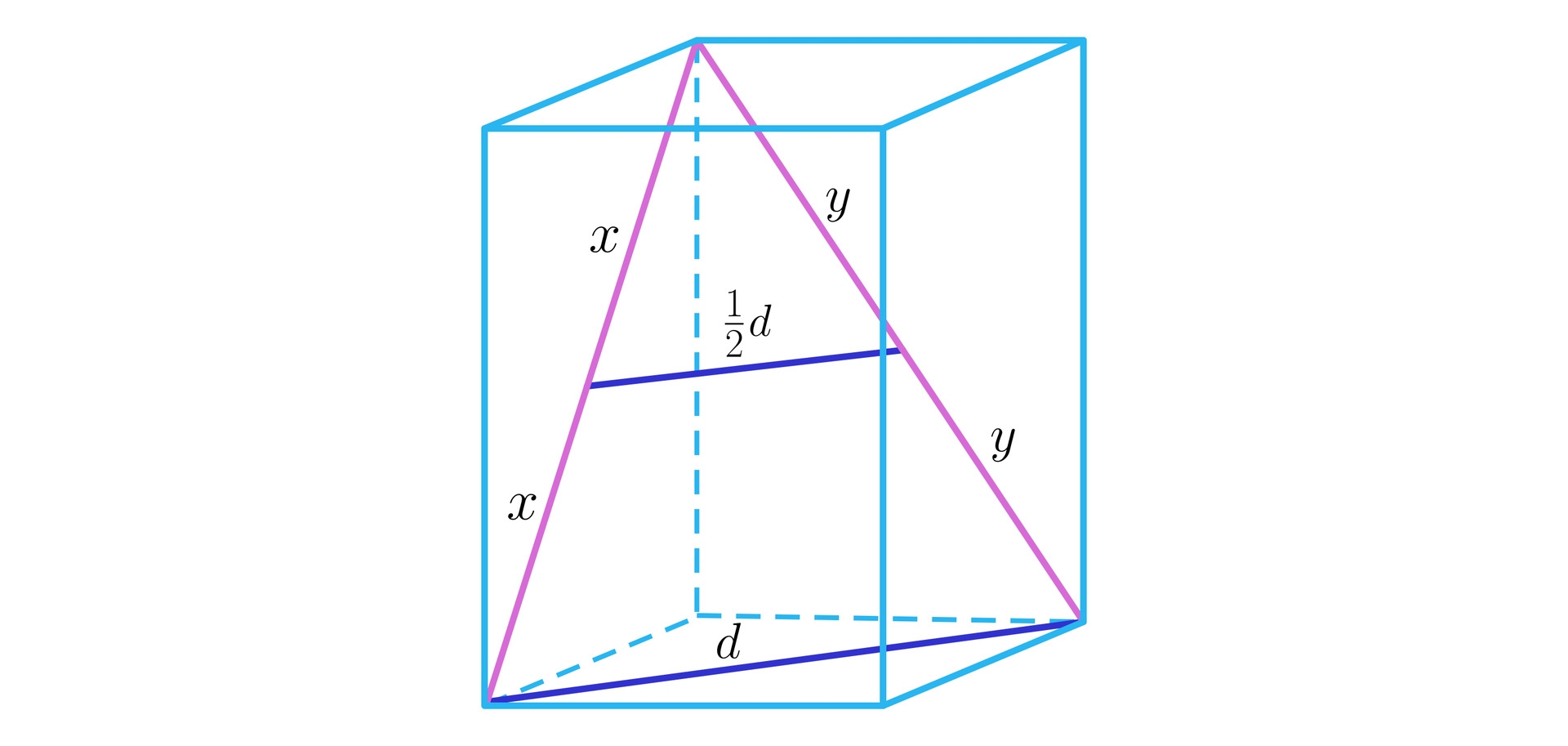
czyli długość odcinka łączącego środki przekątnych sąsiednich ścian bocznych w prostopadłościanie jest równa połowie długości przekątnej podstawy tego prostopadłościanu;
długość odcinka łączącego punkt przecięcia przekątnych dolnej podstawy z jednym z wierzchołków górnej podstawy prostopadłościanu,
R1dbxYNPzE9TD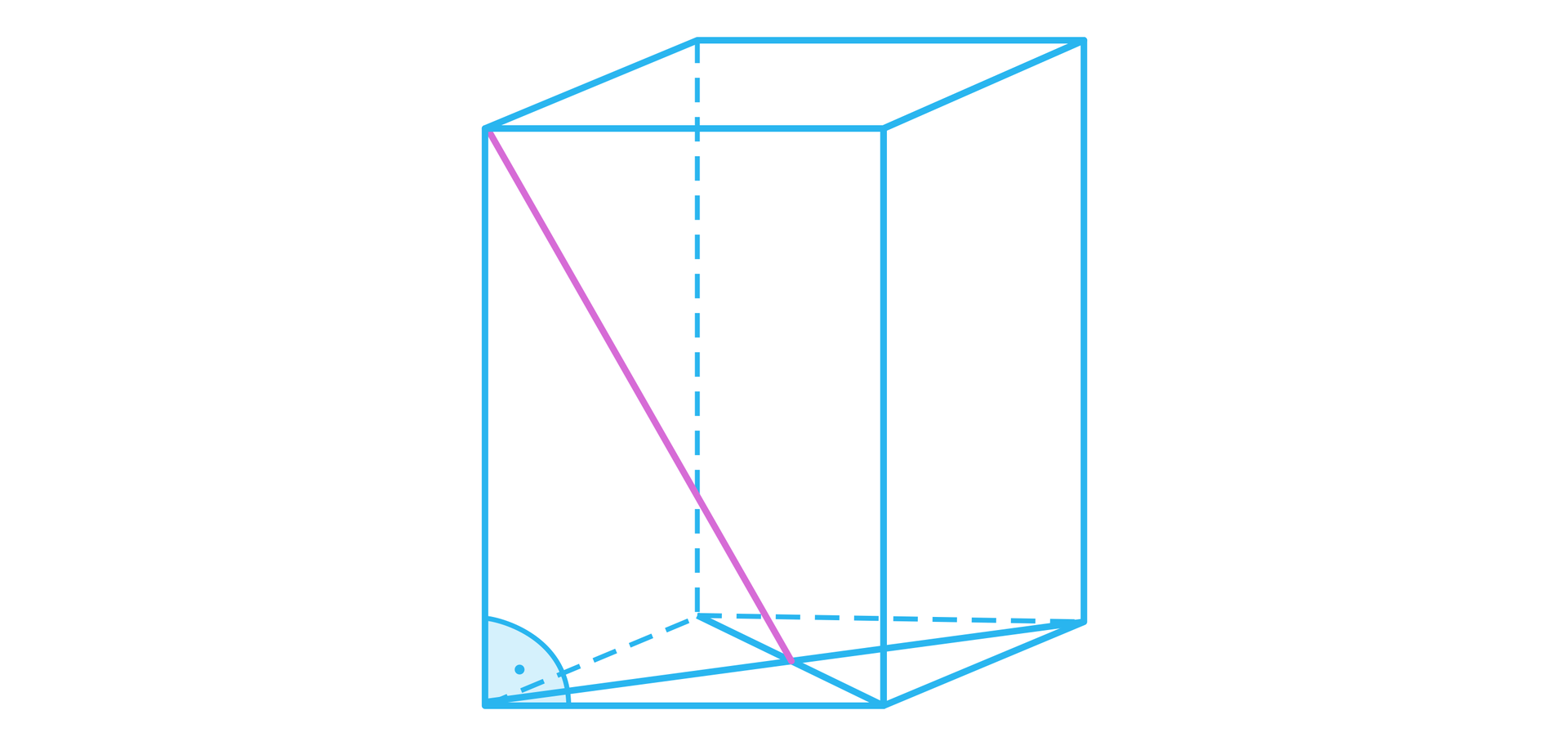
czyli długość odcinka łączącego punkt przecięcia przekątnych dolnej podstawy z jednym z wierzchołków górnej podstawy prostopadłościanu wyznaczamy korzystając z twierdzenia Pitagorasa dot. trójkąta prostokątnego wyznaczonego przez ten odcinek, krawędź boczną oraz odcinek będący połową długości przekątnej podstawy prostopadłościanu.

Przykład 1

Obliczymy długość przekątnej prostopadłościanu o wymiarach: $a = 2 cm$ , $b = 1 cm$ , $c = 2 \sqrt{2} cm$ .

Rozwiązanie:

Podstawmy odpowiednie długości do wzoru na długość przekątnej prostopadłościanu:

$d^{2} = a^{2} + b^{2} + c^{2}$

$d = \sqrt{a^{2} + b^{2} + c^{2}}$

$d = \sqrt{2^{2} + 1^{2} + {(2 \sqrt{2})}^{2}}$

$d = \sqrt{4 + 1 + 8} = \sqrt{13}$

$d = \sqrt{13}$

Przekątna omawianego prostopadłościanu ma długość $\sqrt{13} cm$ .

Przykład 2

Wyznaczymy długości krawędzi prostopadłościanu, jeżeli wiadomo, że jego przekątna ma długość $\sqrt{155}$ , a krawędzie wychodzące z jednego wierzchołka są kolejnymi liczbami nieparzystymi.

Rozwiązanie:

Niech $a, b, c$ będą długościami krawędzi prostopadłościanu, wychodzącymi z jednego wierzchołka.

Ponieważ ich długości są kolejnymi liczbami nieparzystymi, to

$a = 2 n + 1$

$b = 2 n + 3$

$c = 2 n + 5$

gdzie $n \in ℕ_{+}$ .

Skoro przekątna prostopadłościanu ma długość $\sqrt{155}$ , zatem do wyznaczenia wartości $n$ wykorzystamy wzór na długość przekątnej prostopadłościanu:

$d = \sqrt{a^{2} + b^{2} + c^{2}}$

${(\sqrt{155})}^{2} = \sqrt{{(2 n + 1)}^{2} + {(2 n + 3)}^{2} + {(2 n + 5)}^{2}}$

Po podniesieniu obu stron równania do kwadratu otrzymujemy:

$155 = {(2 n + 1)}^{2} + {(2 n + 3)}^{2} + {(2 n + 5)}^{2}$

$155 = 4 n^{2} + 4 n + 1 + 4 n^{2} + 12 n + 9 + 4 n^{2} + 20 n + 25$

$12 n^{2} + 36 n - 120 = 0$

$n^{2} + 3 n - 10 = 0$

$n_{1} = \frac{- 3 - 7}{2} = - 5 < 0$

$n_{2} = \frac{- 3 + 7}{2} = 2 > 0$

Wobec tego krawędzie prostopadłościanu mają długości:

$a = 2 \cdot 2 + 1 = 5$

$b = 2 \cdot 2 + 3 = 7$

$c = 2 \cdot 2 + 5 = 9$

Przykład 3

Obliczymy długość wysokości prostopadłościanu przedstawionego na poniższym rysunku.

RhlcQ5C2MnZ9P

Na ilustracji przedstawiono prostopadłościan. W jego podstawie znajduje się prostokąt o bokach długości 2 i sześć, a jego przekątną oznaczono literą x. Wysokość prostopadłościanu oznaczono literą b. Przekątna całej bryły jest równa 8. Utworzono trójkąt prostokątny o przyprostokątnych b, x, oraz przeciwprostokątnej stanowiącej przekątną całej bryły.

Rozwiązanie :

Zanim wykonamy obliczenia, to przypomnijmy, że wysokość prostopadłościanu jest również jego krawędzią boczną.

Obliczymy najpierw długość przekątnej podstawy prostopadłościanu, korzystając z twierdzenia Pitagorasa:

$x^{2} = 6^{2} + 2^{2}$ , zatem $x = \sqrt{40} = 2 \sqrt{10}$

Obliczamy wysokość prostopadłościanu, korzystając z twierdzenia Pitagorasa:

$x^{2} + b^{2} = 8^{2}$

${(\sqrt{40})}^{2} + b^{2} = 8^{2}$

$b^{2} = 24$

Zatem $b = 2 \sqrt{6}$ .

Wysokość omawianego prostopadłościanu wynosi $2 \sqrt{6}$ .

Przykład 4

Wykażemy, że jeśli krawędzie prostopadłościanu mają długości $a, b, c$ , to długość odcinka $p$ zaznaczonego na poniższym rysunku wyraża się wzorem:

$p = \sqrt{\frac{1}{4} a^{2} + \frac{1}{4} b^{2} + c^{2}}$

Rr6ALMgfJUfRm

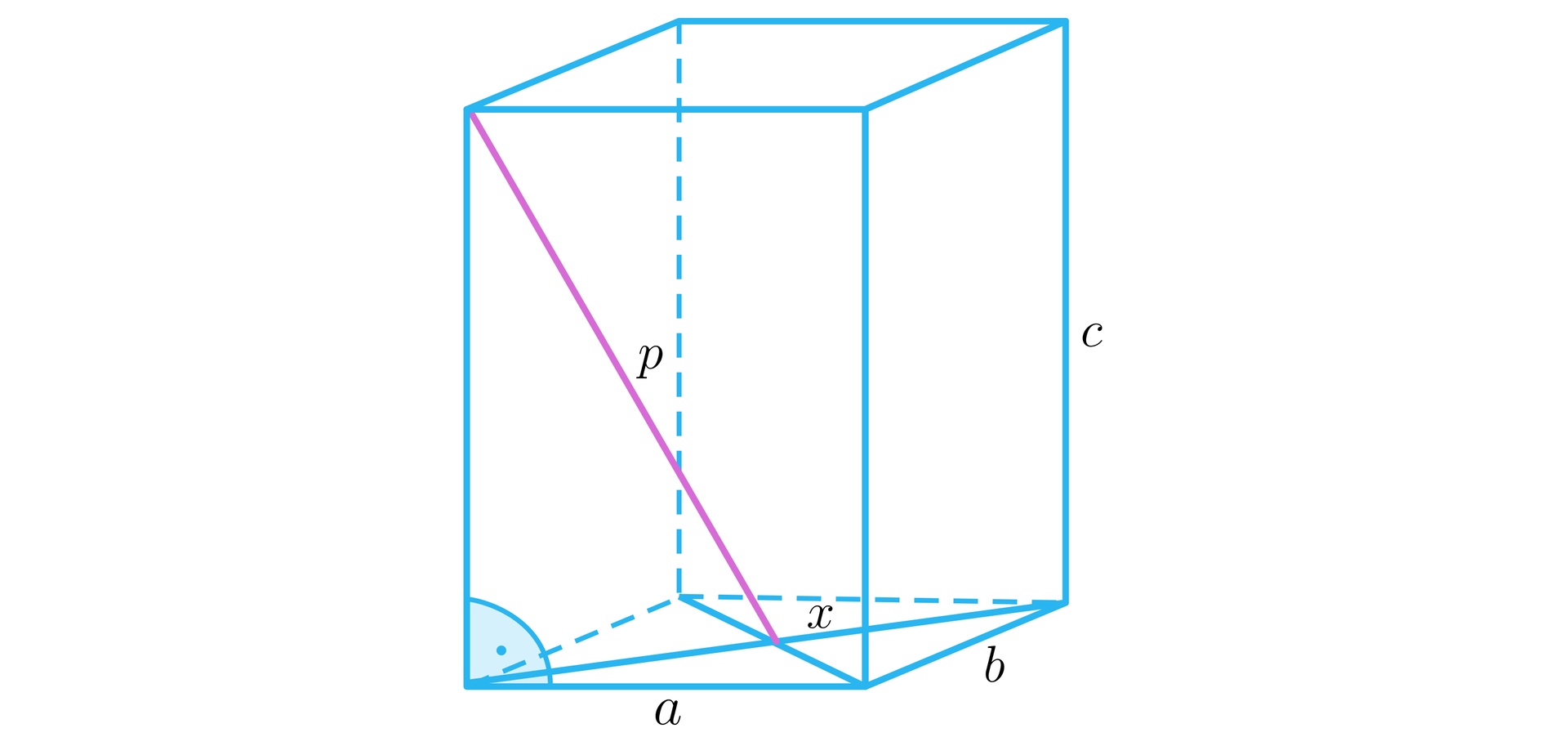
Na ilustracji przedstawiono prostopadłościan o krawędziach podstawy długości a, b oraz wysokości równej c. Zaznaczono odcinek p, łączący jeden z wierzchołków górnej podstawy z punktem x, stanowiącym punkt przecięcia przekątnych dolnej podstawy.

Rozwiązanie:

Jeżeli $x$ jest długością przekątnej podstawy tego prostopadłościanu, to:

$x = \sqrt{a^{2} + b^{2}}$

Korzystając z twierdzenia Pitagorasa, rozwiązujemy równanie:

$p^{2} = {(\frac{1}{2} x)}^{2} + c^{2}$

$p^{2} = \frac{1}{4} x^{2} + c^{2}$

$p^{2} = \frac{1}{4} \cdot {(\sqrt{a^{2} + b^{2}})}^{2} + c^{2}$

$p^{2} = \frac{1}{4} \cdot (a^{2} + b^{2}) + c^{2}$

$p^{2} = \frac{1}{4} a^{2} + \frac{1}{4} b^{2} + c^{2}$

Wobec tego $p = \sqrt{\frac{1}{4} a^{2} + \frac{1}{4} b^{2} + c^{2}}$ .

Przykład 5

Obliczymy długość odcinka łączącego środki przekątnych sąsiednich ścian bocznych w prostopadłościanie, którego podstawa ma wymiary $2$ na $4$ , a krawędź boczna ma długość $6$ .

Rozwiązanie:

Narysujmy prostopadłościan, odpowiednie odcinki oraz wprowadźmy oznaczenia, jak na rysunku.

R1ar0TVyT4Y48

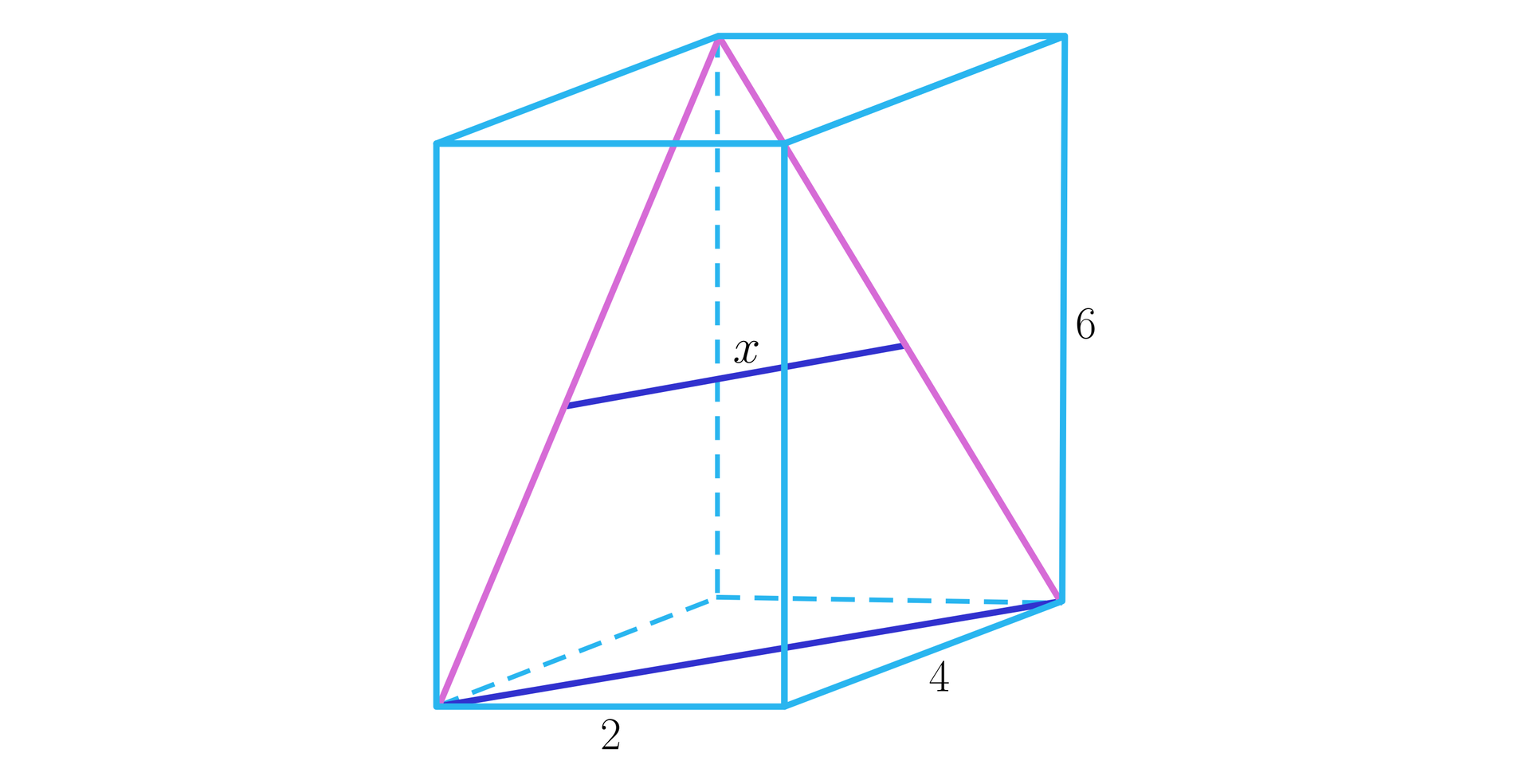
Na ilustracji przedstawiono prostopadłościan o krawędziach podstawy 2 i 4, oraz wysokości równej sześć. Poprowadzono przekątne sąsiednich ścian bocznych, a odcinek łączący ich środki oznaczono literą x. Zaznaczono również przekątną dolnej podstawy.

Ponieważ długość odcinka $x$ jest równa połowie długości przekątnej podstawy prostopadłościanu, zatem

$x = \frac{1}{2} \cdot \sqrt{2^{2} + 4^{2}} = \frac{1}{2} \cdot \sqrt{4 + 16} = \frac{1}{2} \sqrt{20} = \sqrt{5}$

Słownik

prostopadłościan

graniastosłup, którego wszystkie ściany są prostokątami

Wprowadzenie

Infografika

Długości odcinków w prostopadłościanie

Słownik