Przeczytaj

Zaczniemy od przykładu.

Przykład 1

Obliczymy odległość punktu $A = (3, 1)$ od prostej $k$ o równaniu $y = 2 x + 2$ .

RRlbZDo10T0gq

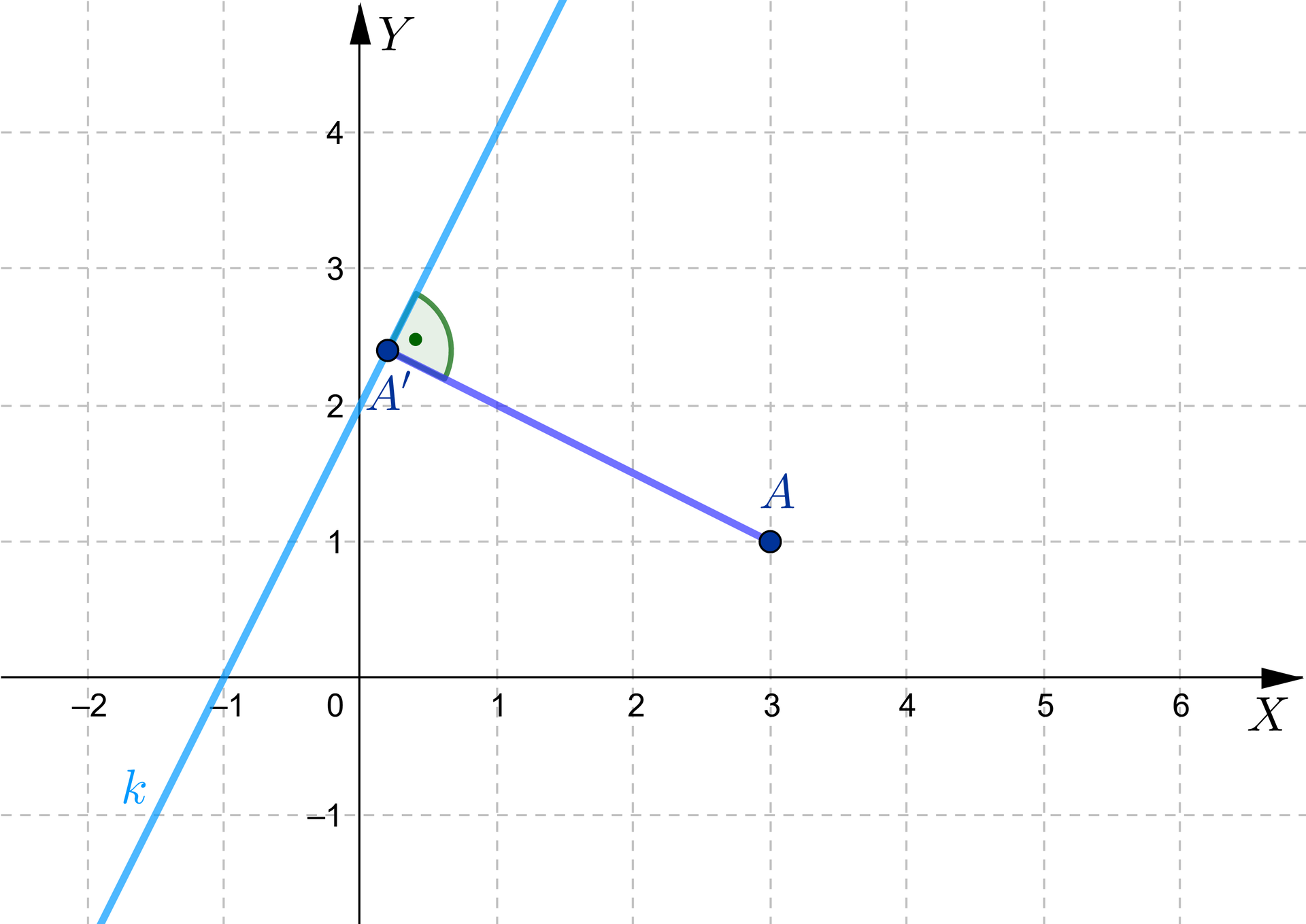
Rysunek przedstawia układ współrzędnych, na który naniesiono prostą k będącą wykresem funkcji y równa się dwa x dodać dwa, punkt A lezący poza prostą k, oraz odcinek łączący punkt A z prostą k. Odcinek tworzy z prostą k kąt prosty w punkcie A prim.

Przypomnijmy, że odległość punktu od prostej jest równa długości odcinka łączącego dany punkt z punktem na prostej, który jest do tej prostej prostopadły.

Zaczniemy od wyznaczenia współrzędnych punktu $A^{'}$ , który należy do prostej $k$ oraz odcinek $A A^{'}$ jest prostopadły do prostej $k$ .

Współczynnik kierunkowy prostej prostopadłej do prostej $k$ jest równy $- \frac{1}{2}$ , zatem równanie prostej prostopadłej do prostej $k$ ma postać

$y = - \frac{1}{2} x + b$

Ponieważ prosta ta przechodzi przez punkty $A = (3, 1)$ , zatem współrzędne punktu $A$ spełniają równanie $y = - \frac{1}{2} x + b$ .

Ten fakt pozwala wyznaczyć wartość współczynnika $b$

$1 = - \frac{1}{2} \cdot 3 + b$

czyli $b = 2, 5$ .

Zatem równanie prostej prostopadłej do prostej $k$ przechodzącej przez punkt $A$ to $y = - \frac{1}{2} x + \frac{5}{2}$ .

Aby wyznaczyć współrzędne punktu wspólnego obu prostych wystarczy rozwiązać układ równań:

$\{\begin{cases} y = 2 x + 2 \\ y = - \frac{1}{2} x + \frac{5}{2} \end{cases}$

Wynika z niego równanie

$2 x + 2 = - 0, 5 x + 2, 5$

$2, 5 x = 0, 5$

$x = 0, 2$

Dla tak wyznaczonej wartości $x$ wartość współrzędnej $y$ jest równa $y = 2 \cdot 0, 2 + 2 = 2, 4$ .

Zatem punkt $A^{'}$ ma współrzędne $(0, 2; 2, 4)$ .

Teraz wystarczy wyznaczyć długość odcinka $A A^{'}$ . W tym celu możemy skorzystać ze wzoru na długość odcinka o danych współrzędnych jego końców:

$|A A^{'}| = \sqrt{{(x_{A^{'}} - x_{A})}^{2} + {(y_{A^{'}} - y_{A})}^{2}} = \sqrt{{(0, 2 - 3)}^{2} + {(2, 4 - 1)}^{2}} =$

$= \sqrt{2, 8^{2} + 1, 4^{2}} = \sqrt{7, 84 + 1, 96} = \sqrt{9, 8} = \frac{7 \sqrt{5}}{5}$

Zatem odległość punktu $A = (3, 1)$ od prostej o równaniu $y = 2 x + 2$ jest równa $\frac{7 \sqrt{5}}{5}$ .

Przykład 2

Postępując analogicznie wyznaczymy wzór na odległość punktu od prostej o równaniu kierunkowymwzór na odległość punktu od prostej o równaniu kierunkowym.

RkMJ2dI5Rb87D

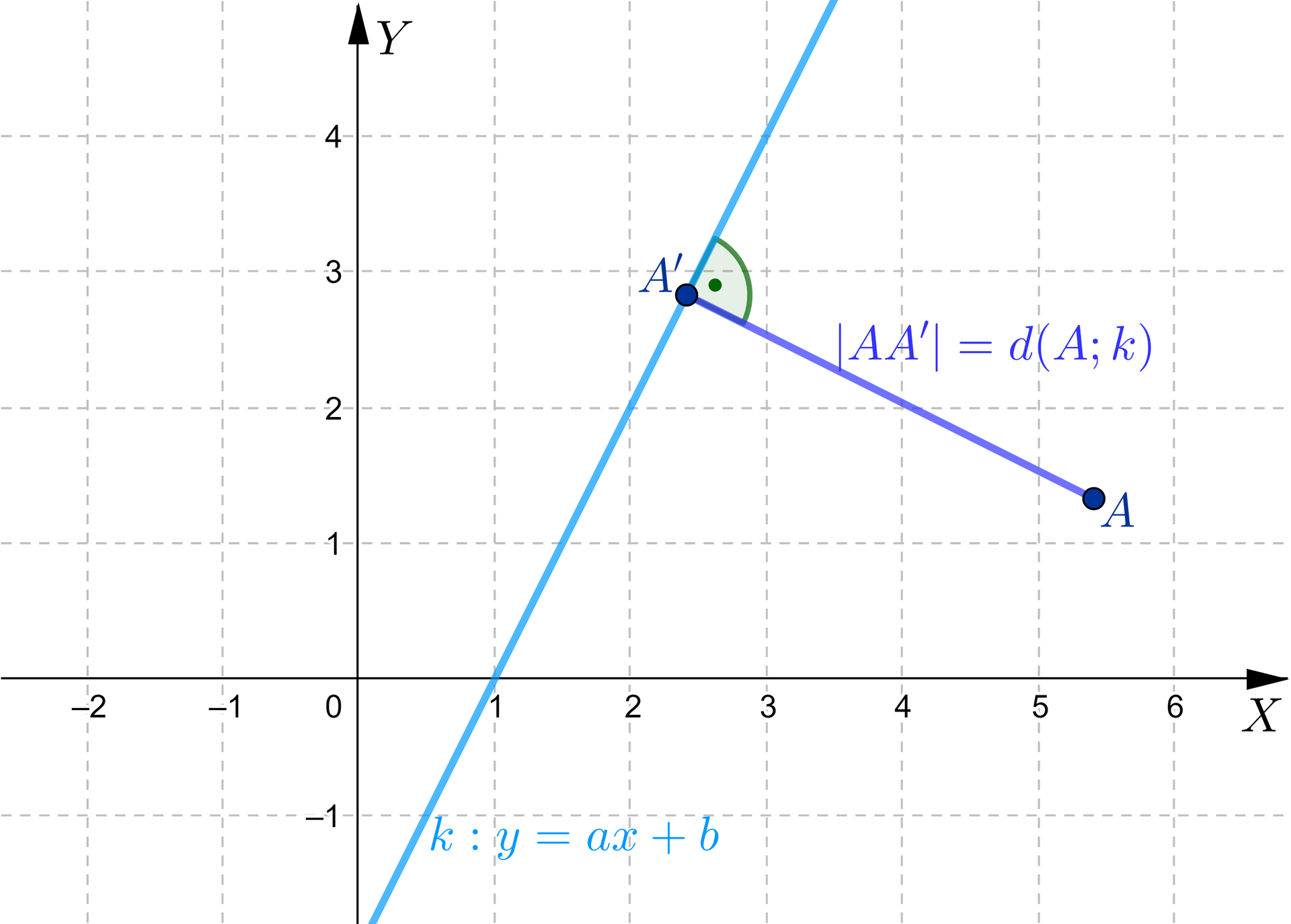
Rysunek przedstawia układ współrzędnych, na który naniesiono prostą k będącą wykresem funkcji y równa się a x dodać b, punkt A lezący poza prostą k, oraz odcinek łączący punkt A z prostą k. Odcinek tworzy z prostą k kąt prosty w punkcie A prim. Długość odcinka oznaczono jako otwarcie wartości bezwzględnej A A prim zamknięcie wartości bezwzględnej równa się d otwarcie nawiasu A średnik k zamknięcie nawiasu.

Rozważmy punkt $A$ o współrzędnych $(x_{0}, y_{0})$ oraz prostą o równaniu $y = a x + b$ .

Wówczas współczynnik kierunkowy prostej prostopadłej do danej jest równy $- \frac{1}{a}$ , zatem równanie tej prostej ma postać $y = - \frac{1}{a} x + B$ .

Współczynnik $B$ wyznaczymy wstawiając do powyższego równania współrzędne punktu $A$ :

$y_{0} = - \frac{1}{a} x_{0} + B$

co oznacza, że:

$B = \frac{a y_{0} + x_{0}}{a}$

Zatem szukane równanie ma postać $y = - \frac{1}{a} x + \frac{a y_{0} + x_{0}}{a}$ .

Aby wyznaczyć współrzędne punktu wspólnego obu prostych, wystarczy rozwiązać układ równań

$\{\begin{cases} y = a x + b \\ y = - \frac{1}{a} x + \frac{a y_{0} + x_{0}}{a} \end{cases}$

Wynika z niego równanie

$a x + b = - \frac{1}{a} x + \frac{a y_{0} + x_{0}}{a}$ , z którego można wyznaczyć $x$ :

$(a + \frac{1}{a}) x = \frac{a y_{0} + x_{0} - a b}{a}$

$x = \frac{a y_{0} + x_{0} - a b}{a^{2} + 1}$

Po podstawieniu wyznaczonej wartości $x$ do równania $y = a x + b$ otrzymujemy

$y = \frac{a^{2} y_{0} + a x_{0} + b}{a^{2} + 1}$

Zatem punkt wspólny $A^{'}$ obu prostych ma współrzędne

$(\frac{a y_{0} + x_{0} - a b}{a^{2} + 1}, \frac{a^{2} y_{0} + a x_{0} + b}{a^{2} + 1})$

Zatem długość odcinka $A A^{'}$ jest równa

$\sqrt{{(\frac{a y_{0} + x_{0} - a b}{a^{2} + 1} - x_{0})}^{2} + {(\frac{a^{2} y_{0} + a x_{0} + b}{a^{2} + 1} - y_{0})}^{2}} =$

$= \sqrt{{(\frac{a y_{0} - a^{2} x_{0} - a b}{a^{2} + 1})}^{2} + {(\frac{a x_{0} - y_{0} + b}{a^{2} + 1})}^{2}} =$

$= \sqrt{\frac{a^{2} {(y_{0} - a x_{0} - b)}^{2} + {(y_{0} - a x_{0} - b)}^{2}}{{(a^{2} + 1)}^{2}}} =$

$= \sqrt{\frac{(a^{2} + 1) {(y_{0} - a x_{0} - b)}^{2}}{{(a^{2} + 1)}^{2}}} =$

$= \sqrt{\frac{{(y_{0} - a x_{0} - b)}^{2}}{a^{2} + 1}} = \frac{|y_{0} - a x_{0} - b|}{\sqrt{a^{2} + 1}}$

Zatem odległość punktu $A = (x_{0}, y_{0})$ od prostej o równaniu $k : y = a x + b$ wyraża się wzorem

$d (A, k) = \frac{|a x_{0} - y_{0} + b|}{\sqrt{1 + a^{2}}}$

Przykład 3

Wyznaczymy odległość punktu $A = (- 1, 3)$ od prostej $k$ o równaniu $y = - 2 x - 1$ .

Podstawiając dane z przykładu do powyższego wzoru otrzymujemy

$d (A, k) = \frac{|- 2 \cdot (- 1) - 3 - 1|}{\sqrt{1 + {(- 2)}^{2}}} = \frac{|- 2|}{\sqrt{5}} = \frac{2 \sqrt{5}}{5}$

Przykład 4

Wyznaczymy wartości parametru $m$ tak, aby punkt o współrzędnych $(m, 2 m)$ był odległy od prostej o równaniu $y = 3 x - 1$ o $2$ .

Podstawiając dane z treści zadania do wzoru

$d (A, k) = \frac{|α x_{0} - y_{0} + b|}{\sqrt{1 + a^{2}}}$

otrzymujemy równanie:

$2 = \frac{|3 m - 2 m - 1|}{\sqrt{1 + 9}}$ , które możemy kolejno przekształcić

$2 \sqrt{10} = |m - 1|$

$2 \sqrt{10} = m - 1$ lub $- 2 \sqrt{10} = m - 1$

$m = 2 \sqrt{10} + 1$ lub $m = 1 - 2 \sqrt{10}$

Zatem szukane punkty mają współrzędne

$(2 \sqrt{10} + 1, 4 \sqrt{10} + 2)$ lub $(1 - 2 \sqrt{10}, 2 - 4 \sqrt{10})$

Jeśli chcemy wyznaczyć odległość punktu $X = (x_{0}, y_{0})$ od prostej $m$ o równaniu $A x + B y + C = 0$ , gdzie $(A, B) \neq (0, 0)$ , możemy posłużyć się wzorem wyprowadzonym powyżej.

Jeśli współczynnik $B$ jest różny od zera, wówczas możemy przekształcić równanie prostej do postaci kierunkowej: $y = - \frac{A}{B} x - \frac{C}{B}$ oraz wykorzystać wzór na odległość punktu od prostej w postaci kierunkowej otrzymując wzór na odległość punktu od prostej opisanej równaniem ogólnymwzór na odległość punktu od prostej opisanej równaniem ogólnym:

$d (X, m) = \frac{|\frac{A}{B} x_{0} + y_{0} + \frac{C}{B}|}{\sqrt{{(\frac{A}{B})}^{2} + 1}}$ , co po przekształceniu daje wzór:

$d (X, m) = \frac{|A x_{0} + B y_{0} + C|}{\sqrt{A^{2} + B^{2}}}$ $(*)$

Jeśli $B = 0$ , to prosta $m$ ma równanie $x = - \frac{C}{A}$ . Wówczas odległość punktu $A$ od prostej $m$ jest równa $|x_{0} + \frac{C}{A}|$ . Zaś wzór $(*)$ sprowadza się do postaci:

$d (X, m) = \frac{|A x_{0} + 0 \cdot y_{0} + C|}{\sqrt{A^{2} + 0^{2}}} = |x_{0} + \frac{C}{A}|$

Oznacza to, że wzór $(*)$ obejmuje również przypadek prostej równoległej do osi $Y$ , zatem jest prawdziwy dla dowolnej prostej i dowolnego punktu umieszczonych w układzie współrzędnych.

Przykład 5

Obliczymy odległość punktu $A = (- 2, - 3)$ od prostej o równaniu $k : 5 x - 4 y + 1 = 0$ .

Zgodnie z powyższym wzorem

$d (A, k) = \frac{|5 \cdot (- 2) - 4 \cdot (- 3) + 1|}{\sqrt{5^{2} + {(- 4)}^{2}}} = \frac{3}{\sqrt{41}} = \frac{3 \sqrt{41}}{41}$

Słownik

wzór na odległość punktu od prostej o równaniu kierunkowym

odległość punktu $X = (x_{0}, y_{0})$ od prostej $k$ o równaniu $y = a x + b$ wyraża się wzorem

$d (X, k) = \frac{|α x_{0} - y_{0} + b|}{\sqrt{a^{2} + 1}}$

wzór na odległość punktu od prostej o równaniu ogólnym

odległość punktu $X = (x_{0}, y_{0})$ od prostej $k$ o równaniu $A x + B y + C = 0$ , gdzie $(A, B) \neq (0, 0)$ , wyraża się wzorem

$d (X, k) = \frac{|A x_{0} + B y_{0} + C|}{\sqrt{A^{2} + B^{2}}}$

Wprowadzenie

Aplet

Słownik