Przeczytaj

Zacznijmy od przypomnienia definicji i najważniejszych własności czworokąta opisanego na okręgu.

Czworokąt opisany na okręgu

Definicja: Czworokąt opisany na okręgu

Jeżeli na okręgu obierzemy cztery różne punkty i poprowadzimy przez nie styczne, to punkty przecięcia kolejnych stycznych będą wierzchołkami czworokąta opisanego na okręgu.

lub inaczej:

Okrąg wpisany w czworokąt

Definicja: Okrąg wpisany w czworokąt

Okrąg, który jest styczny do każdego boku wielokąta.

Odcinki łączące środek okręgu wpisanego z punktami styczności na bokach wielokąta są do nich prostopadłe i są promieniami tego okręgu.

RIdgQjvi4IMyx

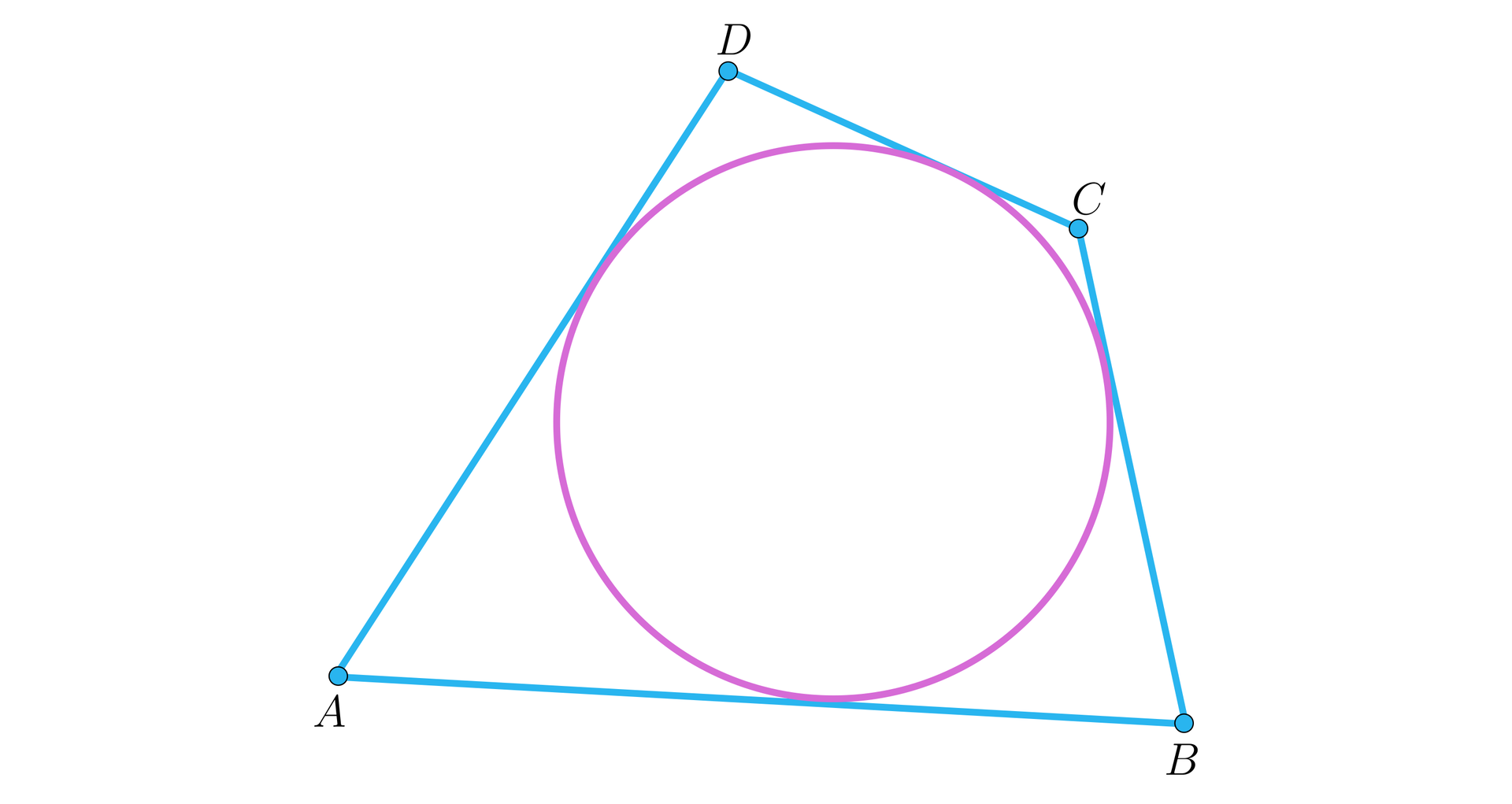
Ilustracja przedstawia okrąg wpisany w czworokąt ABCD.

Warto zauważyć, że nie w każdy czworokąt można wpisać okrąg.

Własności czworokąta opisanego na okręgu

Ważne!

Czworokąt można opisać na okręgu wtedy i tylko wtedy, gdy sumy długości przeciwległych boków tego czworokąta są równe:

|A B| + |C D| = |B C| + |D A|

ReY6mwRSYXrvO

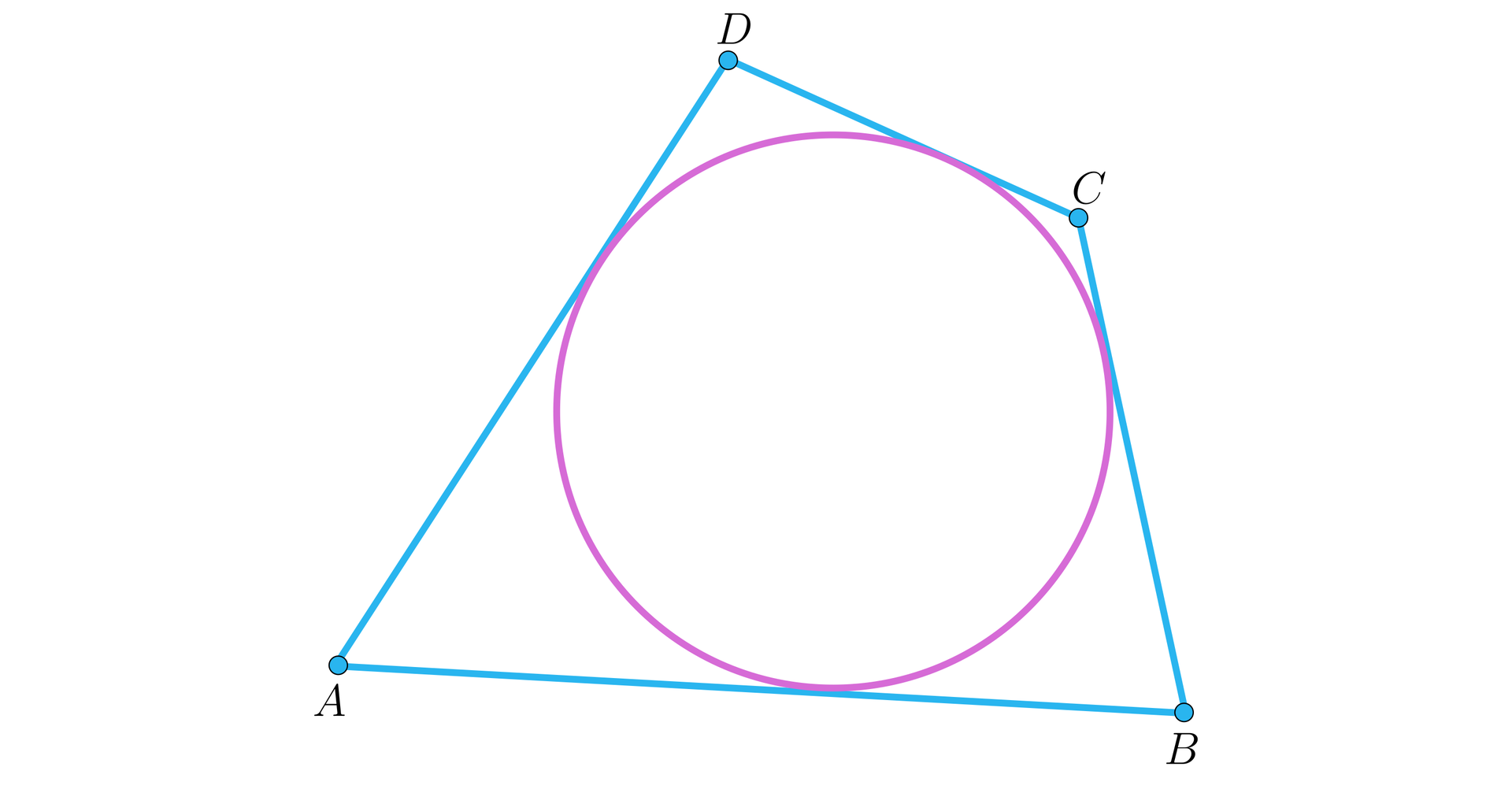
Przypomnijmy, że dowód powyższego twierdzenia opiera się na równości odcinków stycznych.

Dowolny czworokąt można opisać na okręgu wtedy i tylko wtedy, gdy dwusieczne wszystkich jego kątów przecinają się jednym punkcie, który jest środkiem okręgu.

RxaCHG9SHkiwQ

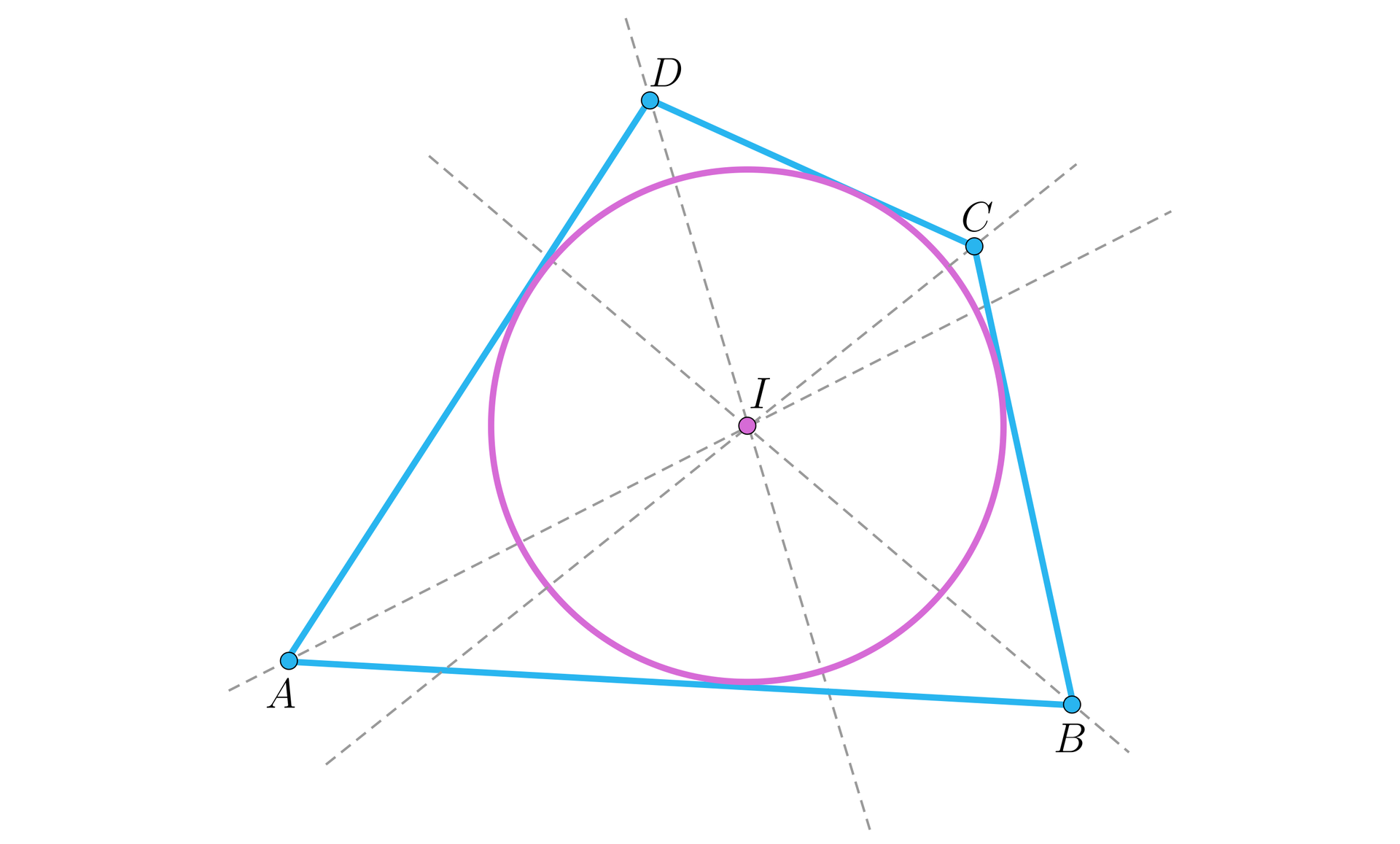
Ilustracja przedstawia okrąg o środku I wpisany w czworokąt ABCD. Przez każdy wierzchołek czworokąta przechodzą dwusieczne które przecinają również środek okręgu.

Z powyższych wzorów wynika, że jeżeli w równoległobok można wpisać okrąg, to jest on rombem.

Pole czworokąta opisanego na okręgu o promieniu

r

Twierdzenie: Pole czworokąta opisanego na okręgu o promieniu

r

Pole czworokąta $A B C D$ opisanego na okręgu o promieniu $r$ wyraża się wzorem:

P = \frac{1}{2} (|A B| + |B C| + |C D| + |D A|) \cdot r

Dowód

R1QxRXFPEowXz

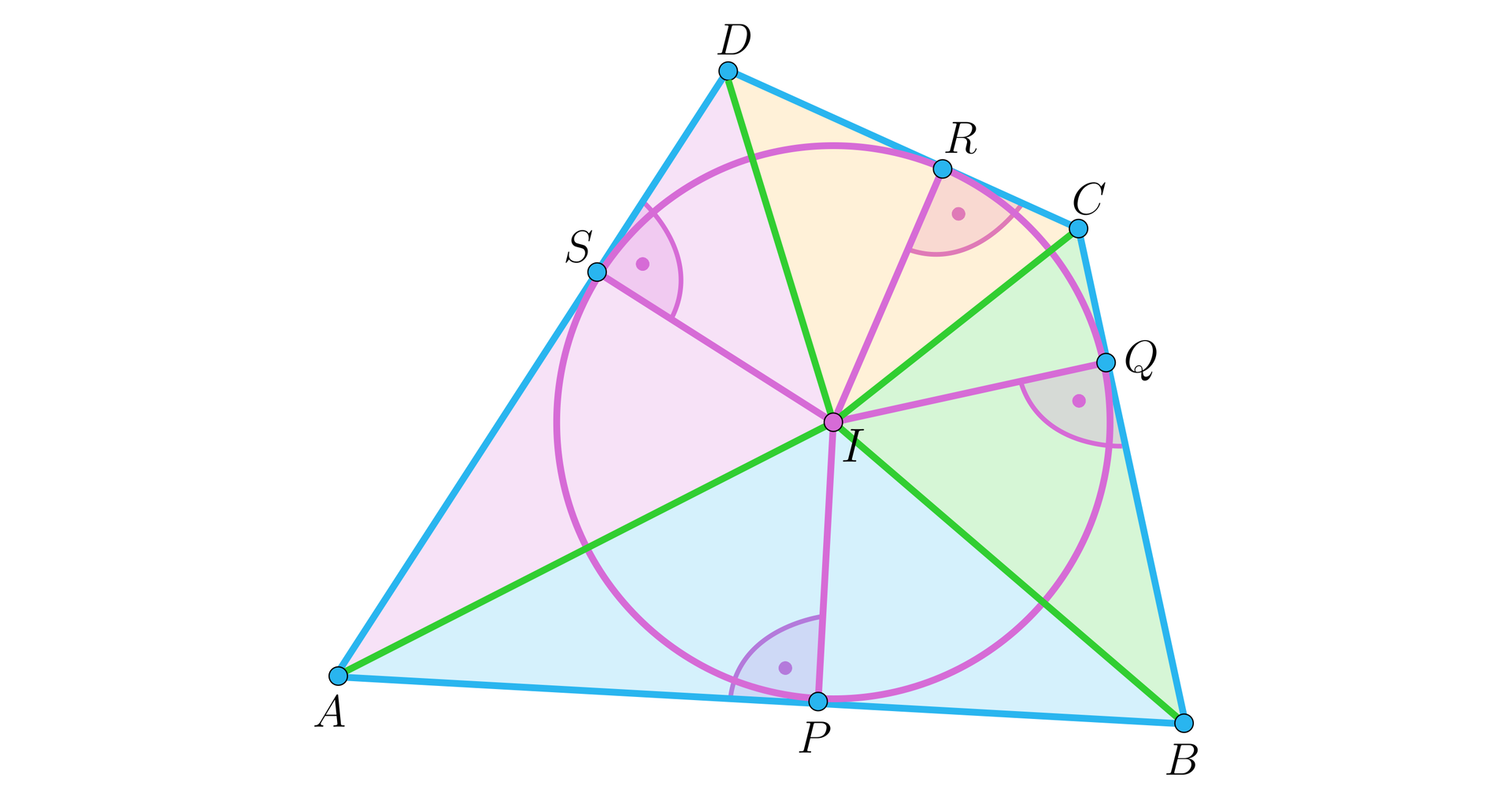
Ilustracja przedstawia okrąg o środku I wpisany w czworokąt ABCD. Środek okręgu i wierzchołki czworokąta są połączone tworząc odcinki AI ,BI ,CI i DI. Promienie okręgu dochodzą do boków czworokąta w punktach styku pod kątem prostym tworząc odcinki: IS, IR, IQ oraz IP. Promień IS dzieli bok AD na odcinki AS i SD , promień IR dzieli bok DC na DR i RC, promień IQ dzieli bok BC na BQ i QC, natomiast promień IP dzieli bok AB na odcinki AP i PB. Trójkąt ADI oznaczono kolorem różowym, DCI pomarańczowym , BCI zielonym oraz ABI niebieskim.

Połączmy wierzchołki czworokąta ze środkiem okręgu. Dostajemy cztery trójkąty, których wysokości są równe promieniowi okręgu. Stosując wzór na pole trójkąta i sumując te cztery trójkąty otrzymujemy:

P = \frac{1}{2} |A B| \cdot r + \frac{1}{2} |B C| \cdot r + \frac{1}{2} |C D| \cdot r + \frac{1}{2} |D A| \cdot r =

= \frac{1}{2} (|A B| + |B C| + |C D| + |D A|) \cdot r

Dla zainteresowanych

Dla czworokątów wpisanych w okrąg i opisanych na okręgu, których długości boków to $a$ , $b$ , $c$ , $d$ pole wyraża się wzorem:

P = \sqrt{a b c d}

Dowód:

Przypomnijmy wzór Brahmagupty na pole czworokąta wpisanego w okrąg:

P = \sqrt{(p - a) (p - b) (p - c) (p - d)}

gdzie $p = \frac{1}{2} (a + b + c + d)$ .

Z drugiej strony, gdy skorzystamy z własności, że w czworokącie opisanym na okręgu sumy długości przeciwległych boków są równe $(a + c = b + d)$ otrzymujemy:

p - a = \frac{1}{2} (a + b + c + d) - a = \frac{1}{2} ((a + c) + (b + d)) - a =

= \frac{1}{2} (a + c + a + c) - a = \frac{1}{2} (2 a + 2 c) - a = a + c - a = c

analogicznie:

p - b = \frac{1}{2} (a + b + c + d) - b = d

p - c = \frac{1}{2} (a + b + c + d) - c = a

p - d = \frac{1}{2} (a + b + c + d) - d = b

P = \sqrt{(p - a) (p - b) (p - c) (p - d)} = \sqrt{a b c d}

Tym samym udowodniliśmy powyższy wzór.

Teraz pokażemy kilka zastosowań własności czworokąta opisanego na okręgu do wyznaczania jego pola. Zacznijmy od następującego, prostego przykładu.

Przykład 1

Wyznaczymy pole czworokąta opisanego na okręgu, którego obwód jest równy $30$ , natomiast promień okręgu wpisanego w ten czworokąt ma długość $3$ .

Rozwiązanie

Podstawiając bezpośrednio do wzoru:

$P = \frac{1}{2} (|A B| + |B C| + |C D| + |D A|) \cdot r = \frac{1}{2} \cdot 30 \cdot 3 = 45$ .

Teraz przećwiczymy wyznaczanie pola czworokąta opisanego na okręgu, w których będziemy korzystać z poznanych wzorów i faktów geometrii płaskiej.

Przykład 2

TrapeztrapezTrapez o kątach przy dłuższej podstawie równych $60 °$ i $90 °$ jest opisany na okręgu o promieniu $4$ . Zastanówmy się, jakie jest pole tego trapezu.

Rozwiązanie

R1NHC8HRTTR69

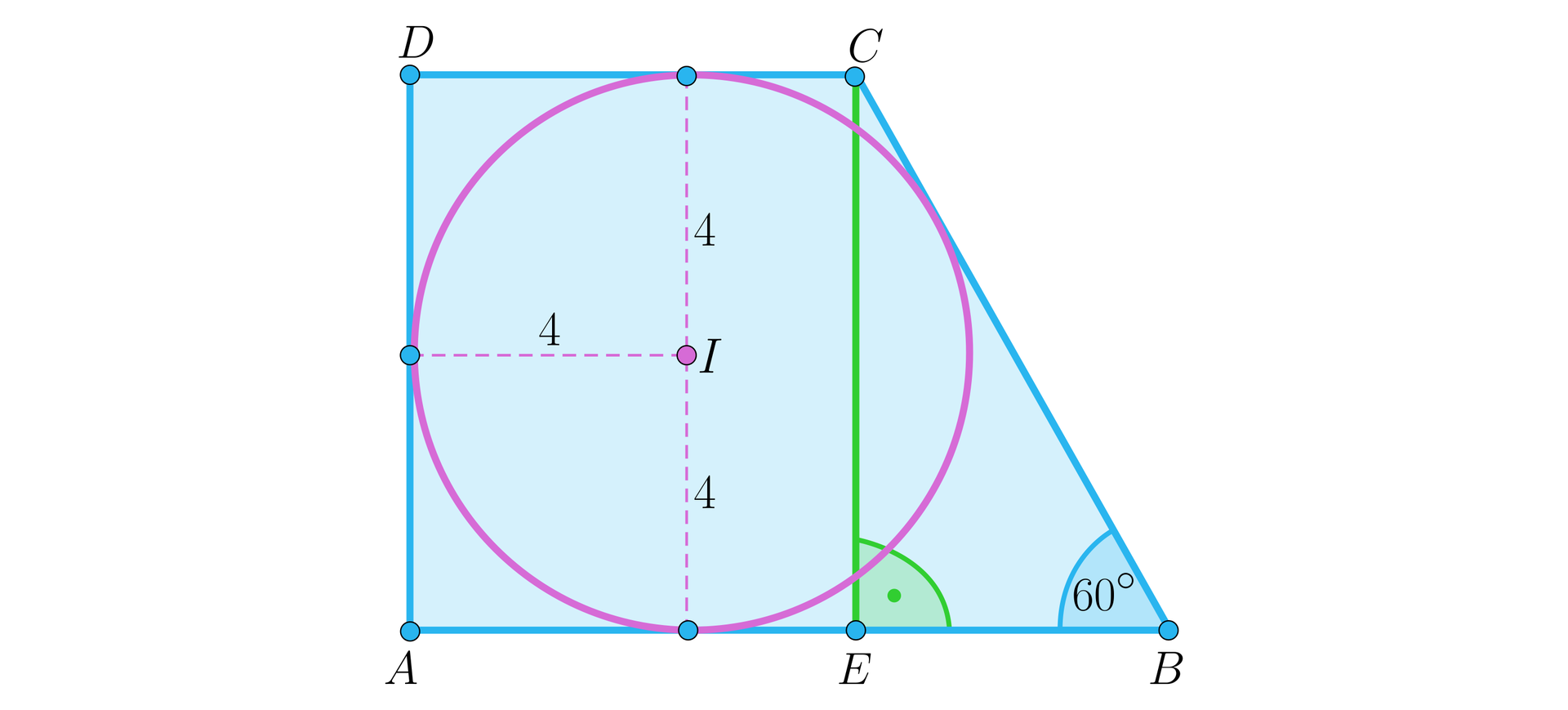
Ilustracja przedstawia trapez prostokątny ABCD w który wpisano okrąg o środku I. Kąty BAD i ADC są kątami prostymi. Z punktu C opuszczono wysokość pod kątem prostym na podstawę AB dzieląc ją na odcinki AE i EB. Kąt CBE ma wartość 60° . Promienie okręgu dochodzące do boków AD, DC i AB mają wartość 4.

Zauważmy, że w trapezie prostokątnym jego wysokość jest równa średnicy okręgu wpisanego, zatem

$|C E| = 2 \cdot 4 = 8$ .

Mając długość boku $C E$ i korzystając z własności trójkąta $E B C$ możemy wyznaczyć długości jego boków:

$|E B| = \frac{8}{\sqrt{3}}$ ,

natomiast

$|C B| = \frac{16}{\sqrt{3}} = \frac{16 \sqrt{3}}{3}$ .

Warto zauważyć, że nie musimy wyznaczać długości podstaw, gdyż suma podstaw potrzebna do wyznaczenia pola jest równa sumie ramion, a to już mamy.

Zatem szukane pole jest równe:

$P = \frac{1}{2} (|A B| + |C D|) \cdot h = \frac{1}{2} (|B C| + |D A|) \cdot h =$

$= \frac{1}{2} (\frac{16 \sqrt{3}}{3} + 8) \cdot 8 = 32 (\frac{2 \sqrt{3}}{3} + 1)$ .

Rozwiążemy teraz dwoma sposobami zadanie typu maturalnego.

Przykład 3

Trapez równoramienny $A B C D$ o długościach podstaw $|A B| = a$ , $|C D| = b$ jest opisany na okręgu. Przyjmijmy, że $a > b$ . Wyznaczymy promień okręgu wpisanego i pole trapezu.

Rozwiązanie

RYrPNkHC1OE4Z

Ilustracja przedstawia trapez ABCD w który wpisano okrąg o środku I. Promień okręgu wynosi r. Krótsza podstawa trapezu DC ma długość b. Na dłuższą podstawę trapezu AB z wierzchołków D i C opuszczono dwie wysokości o wartościach 2r, dzielą one podstawę na odcinki AE , EF i FB. Odcinek EF ma długość b natomiast odcinki AE i FB długość a-b2.

Zauważmy, że jeżeli w trapez równoramienny można wpisać okrąg, to znając długości jego podstaw łatwo jest obliczyć długość ramienia.

Oznaczmy $|A D| = |B C| = c$ .

Wtedy $2 c = a + b$ , więc $c = \frac{a + b}{2}$ .

Poprowadzimy teraz wysokości $E D$ i $C F$ . Widzimy, że czworokąt $E F C D$ jest prostokątem, więc $|E F| = |C D| = b$ .

Zatem $|A E| = |F B| = \frac{a - b}{2}$ .

Z twierdzenia Pitagorasa dla trójkąta $A E D$ lub $F B C$ otrzymujemy:

${(\frac{a - b}{2})}^{2} + {(2 r)}^{2} = {(\frac{a + b}{2})}^{2}$ .

Po sprowadzeniu do wspólnego mianownika i skorzystaniu ze wzorów skróconego mnożenia otrzymujemy:

$4 r^{2} = \frac{a^{2} + 2 a b + b^{2} - (a^{2} - 2 a b + b^{2})}{4} = a b$ .

Zatem $r = \frac{\sqrt{a b}}{2}$ natomiast pole trapezu jest równe:

$P = \frac{1}{2} (a + b) \cdot h = \frac{1}{2} (a + b) \cdot 2 r = \frac{(a + b) \sqrt{a b}}{2}$ .

Teraz pokażemy zupełnie inne podejście do wyznaczenia promienia okręgu wpisanego w ten trapez.

Przykład 4

Trapez równoramienny $A B C D$ o długościach podstaw $|A B| = a$ , $|C D| = b$ jest opisany na okręgu. Przyjmijmy, że $a > b$ . Wyznaczymy promień okręgu wpisanego i pole trapezu.

Rozwiązanie

Zacznijmy od przeanalizowania poniższego rysunku:

RKtgmFgSnKLPM

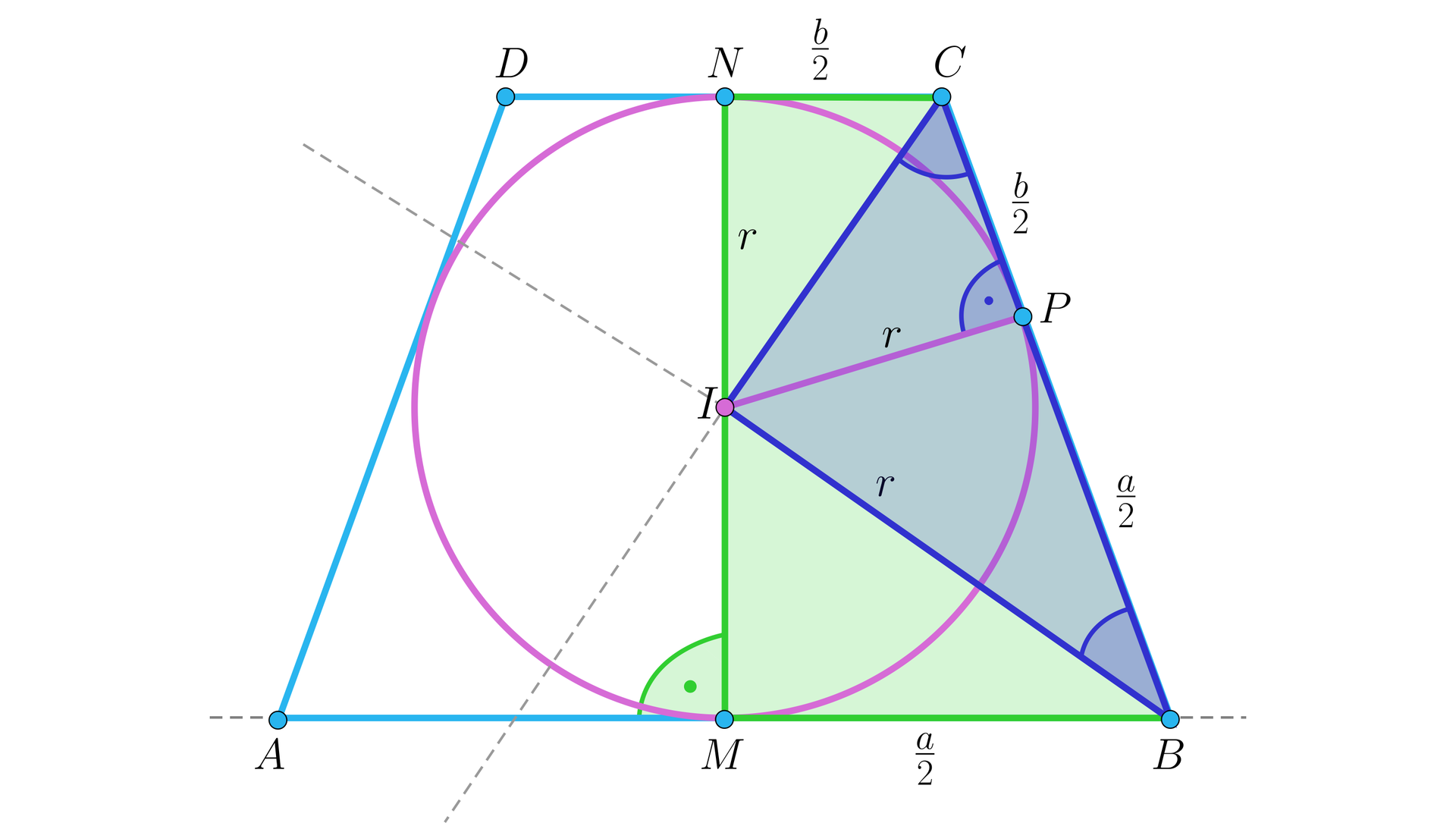
Ilustracja przedstawia trapez ABCD w który wpisano okrąg o środku I. Z okręgu poprowadzono promienie w kierunku boków trapezu tworzące odcinki : promień IN na boku DC tworzy odcinki DN i NC i jest pod kątem prostym do podstawy AB, promień IP na bok CB tworzy odcinki CP i PB i jest pod kątem prostym do ramienia BC oraz promień IM na bok AB tworzący odcinki AM i MB . Poprowadzono również odcinki IC i IB , które tworzą trójkąt CBI oznaczony na niebiesko . Odcinki NC i CP mają długość b2 natomiast odcinki PB i MB a2.

Środek okręgu wpisanego oznaczmy $I$ .

Wiemy, że środek okręgu wpisanego w wielokąt wypukły leży na dwusiecznych kątów wewnętrznych, zatem proste $B I$ oraz $C I$ są dwusiecznymi kątów przy wierzchołkach $B$ i $C$ trapezu $A B C D$ .

Wiemy też, że suma miar kątów wewnętrznych leżących przy tym samym ramieniu dowolnego trapezu jest równa $180 °$ , więc suma kątów $C B I$ oraz $B C I$ jest równa połowie tej sumy, a więc $90 °$ . Trójkąt $B C I$ jest zatem trójkątem prostokątnym, o kącie prostym przy wierzchołku $I$ .

Wysokość $I P$ z wierzchołka kąta prostego jest więc średnią geometryczną odcinków, na jakie podzieliła podstawę $B C$ trójkąta $I B C$ :

$I P = r = \sqrt{B P \cdot C P}$ .

Teraz wystarczy, że zastosujemy twierdzenie o odcinkach stycznych i zauważymy równość odcinków:

$|B P| = |B M| = \frac{1}{2} a$

oraz

$|C P| = |C N| = \frac{1}{2} b$ .

Ostatecznie otrzymujemy:

$r = \sqrt{\frac{1}{2} a \cdot \frac{1}{2} b} = \frac{1}{2} \sqrt{a b}$ .

Mając długość promienia i podstaw analogicznie jak w poprzednim przykładzie wyznaczamy pole trapezu, które jest równe

$P = \frac{(a + b) \sqrt{a b}}{2}$ .

Teraz przeanalizujemy problem, który będzie lekką modyfikacją innego zadania typu maturalnego.

Przykład 5

W czworokąt $A B C D$ , w którym $|A D| = 5 \sqrt{3}$ i $|C D| = 6$ można wpisać okrąg. Przekątna $B D$ tworzy z bokiem $A B$ czworokąta kąt o mierze $60 °$ , natomiast z bokiem $A D$ kąt, którego sinus jest równy $\frac{3}{4}$ . Wyznacz pole tego czworokąta.

Rozwiązanie

R3PCD3ddzv9Xf

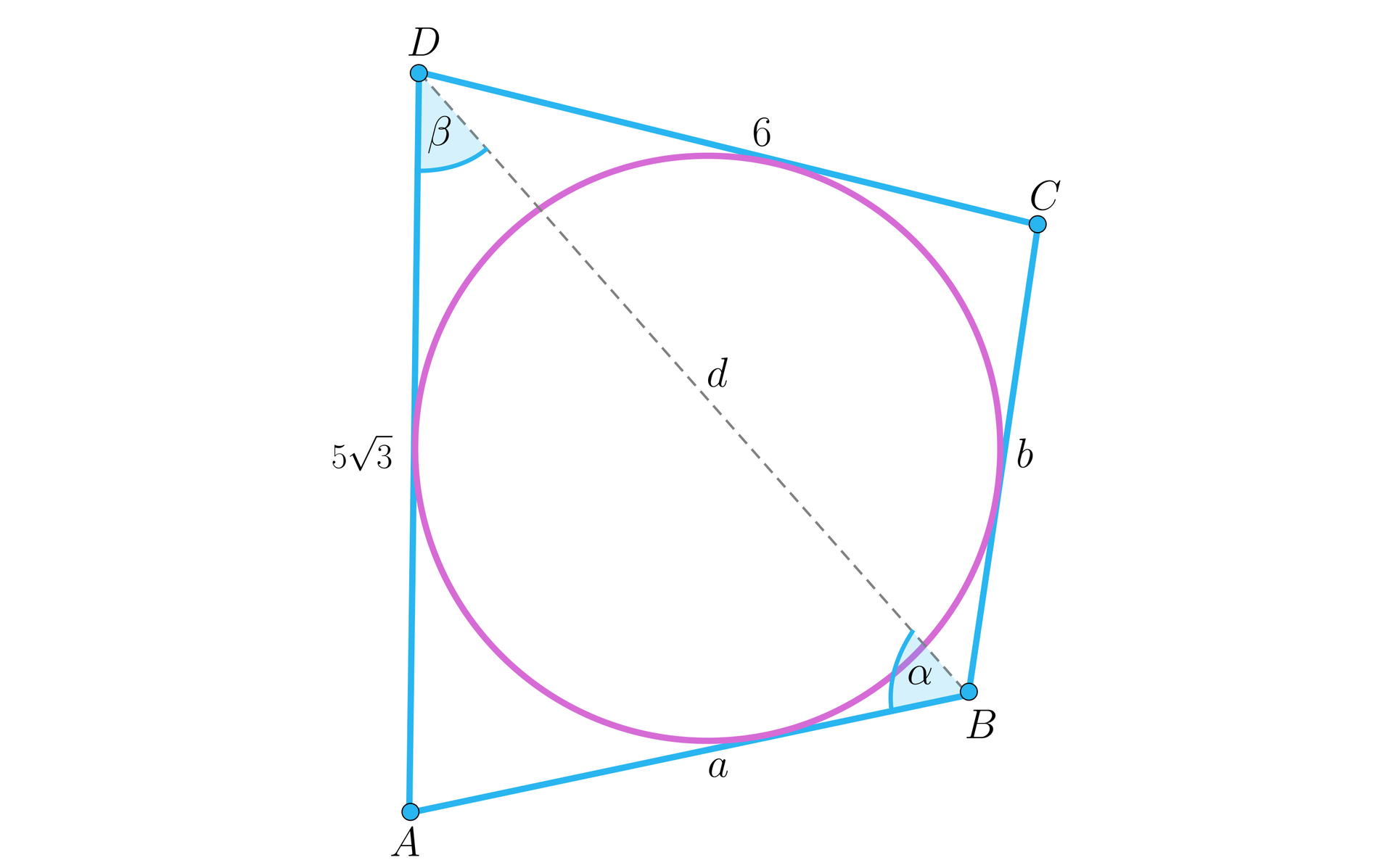
Ilustracja przedstawia okrąg wpisany w czworokąt ABCD. Przekątna DB ,oznaczona linią przerywaną ma długość d. Bok DC ma długość 6 , bok BC ma długość b , bok AB ma długość a natomiast bok AD ma długość 53. Kąt ABD ma wartość α a kąt ADB ma wartość β.

Przyjmujemy oznaczenia jak na rysunku: $α = 60 °$ , $\sin β = \frac{3}{4}$ , $|A B| = a$ , $|B C| = b$ , $|B D| = d$ .

Widzimy, że znając dwa kąty (lub wartości funkcji trygonometrycznej) oraz długość boku w trójkącie $A B D$ możemy ten trójkąt rozwiązać.

Skorzystajmy z twierdzenia sinusów do wyznaczenia długości boku $|A B| = a$ :

$\frac{a}{\sin β} = \frac{5 \sqrt{3}}{\sin α}$ ,

$\frac{a}{\frac{3}{4}} = \frac{5 \sqrt{3}}{\frac{\sqrt{3}}{2}}$ ,

$a = \frac{15}{2}$ .

Skorzystajmy z twierdzenia cosinusów do wyznaczenia długości przekątnej $|B D| = d$ :

${(5 \sqrt{3})}^{2} = d^{2} + {(\frac{15}{2})}^{2} - 2 d \frac{15}{2} \cos 60 °$ .

Rozwiązujemy powyższe równanie kwadratowe. Jego dodatnie rozwiązanie to długość przekątnej $B D$ :

$d = \frac{15 + 5 \sqrt{21}}{4}$ .

Z twierdzenia o czworokącie opisanym na okręgu wyznaczamy długość boku $b$ :

$b + 5 \sqrt{3} = \frac{15}{2} + 6$ ,

$b = \frac{27 - 10 \sqrt{3}}{2}$ .

Znając już wszystkie boki i przekątną czworokąta możemy wyznaczyć jego pole.

Podamy algorytm do wyznaczenia tego pola, gdyż większość boków to liczby niewymierne i uciążliwe rachunki mogłyby przysłonić ideę jego wyznaczania:

Zauważamy, że pole czworokąta jest równe sumie pól dwóch trójkątów: $A B D$ i $B C D$ .

Pole trójkąta $A B C$ łatwo obliczamy ze wzoru:

$\frac{1}{2} |A D| \cdot |B D| \cdot \sin β$ .

Natomiast, aby wyznaczyć pole trójkąta $D B C$ wyznaczamy wartość cosinusa dowolnego kąta (z twierdzenia cosinusów).

Następnie, z jedynki trygonometrycznej, wyznaczamy sinus tego kąta.

Teraz stosujemy (ten sam co poprzednio) wzór na pole trójkąta $D B C$ .

Szukane pole czworokąta $A B C D$ to, jak wspomnieliśmy, suma tych dwóch wyznaczonych pól.

Słownik

trapez

czworokąt (wypukły) mający przynajmniej jedną parę równoległych boków; (wybraną) parę boków równoległych nazywa się podstawami, pozostałe boki noszą nazwę ramion, odległość między podstawami nazywa się wysokością trapezu

Wprowadzenie

Galeria zdjęć interaktywnych

Własności czworokąta opisanego na okręgu

Słownik