Przeczytaj

Już wiesz

R1XmU9URp06Qw

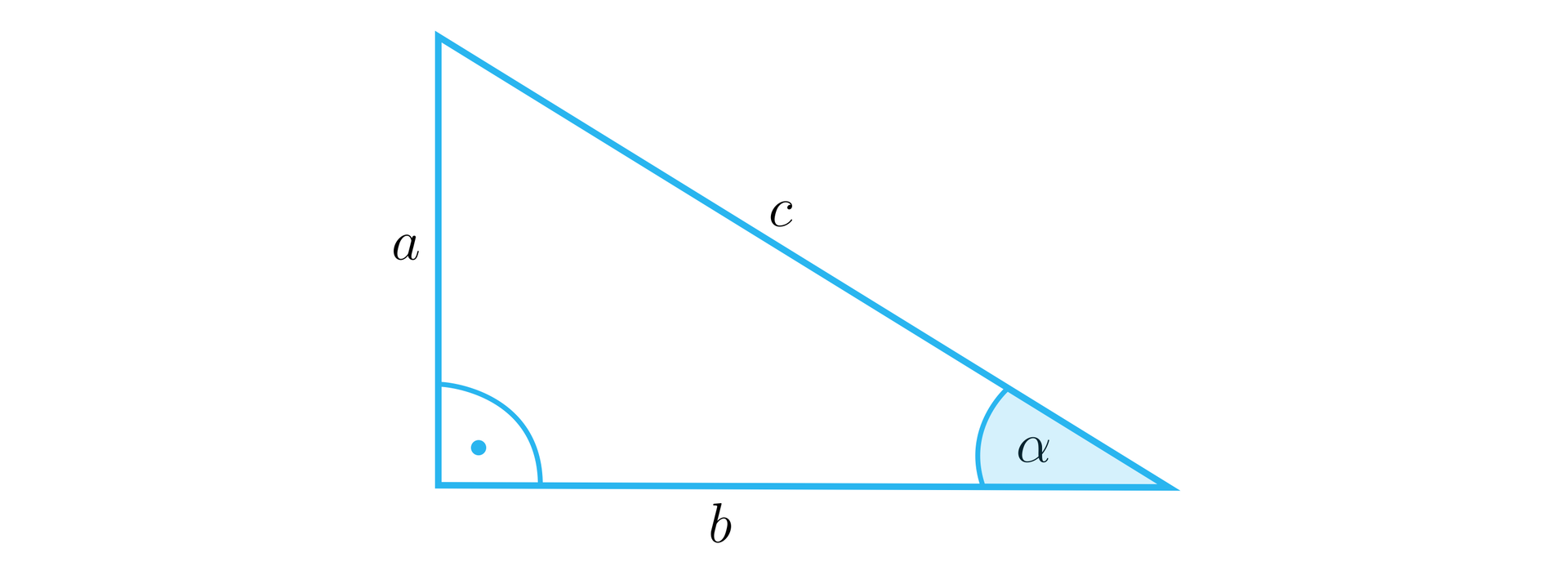
Rysunek przedstawia trójkąt prostokątny o podstawie b, pionowej przyprostokątnej a oraz o przeciwprostokątnej c. Zaznaczono także dwa kąty wewnętrzne trójkąta. Kąt prosty między bokami a i b oraz kąt α między bokami b i c.

Sinusem kąta ostrego $α$ nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej.

Cosinusem kąta ostrego $α$ nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.

Tangensem kąta ostrego $α$ nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przyprostokątnej leżącej przy tym kącie.

Z powyższych definicji mamy, że:

\sin α = \frac{a}{c}

\cos α = \frac{b}{c}

tg α = \frac{a}{b}

Ważne!

Wartość drugiego kąta ostrego w podanym trójkącie wynosi $90 ° - α$ . Zatem:

\sin (90^{\circ} - α) = \frac{b}{c}

\cos (90 ° - α) = \frac{a}{c}

tg (90 ° - α) = \frac{b}{a}

Porównując z powyższymi zależnościami, mamy następujące wzory:

\sin (90 ° - α) = \cos α

\cos (90 ° - α) = \sin α

tg (90 ° - α) = \frac{1}{tg α}

Przykład 1

Równość $\frac{\sin 20 ° + \cos 70 °}{- \cos 70 °}$ możemy zapisać jako $\frac{\sin 20 ° + \sin 20 °}{- \sin 20 °} = \frac{2 \sin 20 °}{- \sin 20 °} = - 2$ .

Przykład 2

Wyrażenie

$(1 - \sin (90 ° - α)) (1 + \sin (90 ° - α))$

po przekształceniu wynosi

$(1 - \cos α) (1 + \cos α) = 1 - \cos^{2} α = \sin^{2} α$ .

Związki między funkcjami trygonometrycznymi kąta ostrego

Twierdzenie: Związki między funkcjami trygonometrycznymi kąta ostrego

Dla dowolnego kąta ostrego $α$ zachodzą następujące zależności:

a) $\sin^{2} α + \cos^{2} α = 1$ (jedynka trygonometryczna),

b) $tg α = \frac{\sin α}{\cos α}$ .

Dowód

RWFnjMG40EOxT

a) Z rysunku możemy odczytać, że: $\sin α = \frac{a}{c}$ oraz $\cos α = \frac{b}{c}$ .

Zatem mamy:

$\sin^{2} α + \cos^{2} α = {(\frac{a}{c})}^{2} + {(\frac{b}{c})}^{2} = \frac{a^{2}}{c^{2}} + \frac{b^{2}}{c^{2}} = \frac{a^{2} + b^{2}}{c^{2}} = \frac{c^{2}}{c^{2}} = 1$ .

b) Z rysunku odczytujemy, że $tg α = \frac{a}{b}$ .

Z definicji sinusa oraz cosinusa kąta $α$ mamy, że:

$tg α = \frac{a}{b} = \frac{\frac{a}{c}}{\frac{b}{c}} = \frac{\sin α}{\cos α}$ .

Ważne!

Z powyższego twierdzenia mamy zależność:

\frac{1}{tg α} = \frac{\cos α}{\sin α}

Przykład 3

Wyznaczymy wartości funkcji trygonometrycznych kąta ostrego $α$ , jeżeli wiadomo, że $\cos (90 ° - α) = \frac{1}{4}$ .

Z zależności w trójkącie prostokątnym mamy, że $\cos (90 ° - α) = \sin α$ , zatem $\sin α = \frac{1}{4}$ .

Po podstawieniu do jedynki trygonometrycznej mamy, że ${(\frac{1}{4})}^{2} + \cos^{2} α = 1$ .

Otrzymujemy, że $\cos^{2} α = \frac{15}{16}$ , zatem $\cos α = \frac{\sqrt{15}}{4}$ lub $\cos α = - \frac{\sqrt{15}}{4}$ .

Ponieważ $α$ jest kątem ostrym, więc $\cos α = \frac{\sqrt{15}}{4}$ .

Zatem $tg α = \frac{\sin α}{\cos α} = \frac{\frac{1}{4}}{\frac{\sqrt{15}}{4}} = \frac{1}{\sqrt{15}} = \frac{\sqrt{15}}{15}$ .

Przykład 4

Uprościmy wyrażenie $(\frac{1}{\sin α} + \frac{1}{\cos α}) tg α$ .

Stosując zależności pomiędzy funkcjami trygonometrycznymi mamy, że:

$(\frac{1}{\sin α} + \frac{1}{\cos α}) tg α = \frac{\sin^{2} α + \cos^{2} α}{\sin α \cos α} tg α = \frac{1}{\sin α \cos α} \cdot \frac{\sin α}{\cos α} = \frac{1}{\cos^{2} α}$ .

Przykład 5

Wyznaczymy wartość wyrażenia $\cos α tg α$ , jeżeli $\cos α = \frac{\sqrt{2}}{3}$ oraz $α$ jest kątem ostrym.

Po przekształceniu wyrażenie $\cos α tg α$ jest postaci $\cos α tg α = \cos α \frac{\sin α}{\cos α} = \sin α$ .

Wartość $\sin α$ wyznaczymy z jedynki trygonometrycznej.

Zatem mamy: $\sin^{2} α + {(\frac{\sqrt{2}}{3})}^{2} = 1$ .

Z obliczeń mamy, że $\sin^{2} α = \frac{7}{9}$ , więc $\sin α = \frac{\sqrt{7}}{3}$ lub $\sin α = - \frac{\sqrt{7}}{3}$ .

Ponieważ $α$ jest kątem ostrym, zatem $\sin α = \frac{\sqrt{7}}{3}$ .

Szukana wartość wyrażenia wynosi $\frac{\sqrt{7}}{3}$ .

Przykład 6

Czy istnieje kąt ostry $α$ , dla którego $tg α = \frac{\sqrt{2}}{3}$ oraz $\cos α = \frac{1}{4}$ ?

W celu sprawdzenia, czy istnieje taki kąt, wyznaczymy wartość $\sin α$ , a następnie wykorzystamy jedynkę trygonometrycznąjedynka trygonometrycznajedynkę trygonometryczną.

Zatem mamy: $tg α = \frac{\sin α}{\cos α}$ .

Podstawiając, otrzymujemy równanie: $\frac{\sqrt{2}}{3} = \frac{\sin α}{\frac{1}{4}}$ , więc $\sin α = \frac{\sqrt{2}}{12}$ .

Sprawdzamy, czy zachodzi równość $\sin^{2} α + \cos^{2} α = 1$ .

Po podstawieniu mamy: ${(\frac{\sqrt{2}}{12})}^{2} + {(\frac{1}{4})}^{2} = \frac{1}{72} + \frac{1}{16} = \frac{11}{144} \neq 1$ .

Zatem nie istnieje taki kąt.

Słownik

jedynka trygonometryczna

\sin^{2} α + \cos^{2} α = 1

Wprowadzenie

Infografika

Słownik