Ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$, zwaną ilorazem ciągu.

Kwadrat o boku $a$ rozcięto na dwa prostokąty o równych polach. Jeden z tych prostokątów rozcięto na dwa jednakowe kwadraty, z których jeden rozcięto znowu na dwa prostokąty o równych polach itd.

RTw6qlhcNBB46

Ilustracja przedstawia kwadrat o boku a. Jest on dzielony na połowy w nieskończoność tak, że tworzą się co raz mniejsze prostokąty P1, P2, P3 i tak dalej.

W ten sposób otrzymano ciąg figur – na przemian prostokątów i kwadratów o polach:

$P_1=\frac{1}{2}a·a=\frac{1}{2}{a}^2$

$P_2=\frac{1}{2}a·\frac{1}{2}a=\frac{1}{4}{a}^2$

$P_3=\frac{1}{2}a·\frac{1}{4}a=\frac{1}{8}{a}^2$

$P_4=\frac{1}{4}a·\frac{1}{4}a=\frac{1}{16}{a}^2$

$P_5=\frac{1}{4}a·\frac{1}{8}a=\frac{1}{32}{a}^2$

$...$

Ciąg liczb określających pola tych figur:

$\frac{1}{2}{a}^2$, $\frac{1}{4}{a}^2$, $\frac{1}{8}{a}^2$, $\frac{1}{16}{a}^2$, $\frac{1}{32}{a}^2$, $...$, $\frac{1}{2^n}{a}^2$, $...$

jest ciągiem geometrycznym nieskończonym o pierwszym wyrazie $\frac{1}{2}{a}^2$ i ilorazie $q=\frac{1}{2}$.

Zauważmy, że gdybyśmy dodali dowolnie dużo tych wyrazów do siebie, np. sto tysięcy, to i tak otrzymana suma nie będzie większa od $a^2$ (wszystkie figury mieszczą się w kwadracie o boku $a$).

W kwadrat o boku $a$ wpisano koło. W koło to wpisano kwadrat, w który znów wpisano koło, itd. W ten sposób określony został ciąg kwadratów. Obliczymy długość boku i pole dziesiątego z tak otrzymanych kwadratów.

R2yL4enCCHo9V

Rysunek przedstawia kwadrat o boku a z wpisanym okręgiem. W okrąg wpisano kwadrat, w którym wykreślono przekątną pokrywającą się z promieniem dużego okręgu. W kwadrat ten wpisano kolejny okrąg i wykreślono w nim promień.

Niech $\left(a_1, a_2, a_3, ...\right)$ będzie ciągiem, którego wyrazami są długości boków kolejnych kwadratów.

Zauważmy, że promień $r$ koła wpisanego w $n$–ty kwadrat równy jest połowie przekątnej $\left(n+1\right)$–go kwadratu.

Wynika z tego, że;

$a_1=a$

$a_2=\frac{a}{\sqrt{2}}$

$a_3=\frac{a_2}{\sqrt{2}}=\frac{a}{2}$

$a_4=\frac{a_3}{\sqrt{2}}=\frac{a}{2\sqrt{2}}$

$a_5=\frac{a_4}{\sqrt{2}}=\frac{a}{4}$

$a_6=\frac{a_5}{\sqrt{2}}=\frac{a}{4\sqrt{2}}$

$...$

Wnioskujemy, że ciąg, którego wyrazami są długości boków kolejnych kwadratów, to:

$a$, $\frac{a}{\sqrt{2}}$, $\frac{a}{2}$, $\frac{a}{2\sqrt{2}}$, $\frac{a}{4}$, $\frac{a}{4\sqrt{2}}$, $...$

Jest on ciągiem geometrycznym, którego pierwszy wyraz jest równy $a$, natomiast iloraz ciągu jest równy $q=\frac{1}{\sqrt{2}}$.

Wzór ogólny ciągu można więc zapisać w postaci

$a_n=\frac{a}{{\left(\sqrt{2}\right)}^{n-1}}$

Obliczamy dziesiąty wyraz tego ciągu, czyli długość boku dziesiątego kwadratu.

$a_{10}=\frac{a}{{\left(\sqrt{2}\right)}^9}=\frac{a}{16\sqrt{2}}$

Niech $\left(b_1, b_2, b_3, ...\right)$ będzie ciągiem liczb określających pola kolejnych kwadratów.

Zatem:

$b_1=a^2$

$b_2=\frac{a^2}{2}$

$b_3=\frac{a^2}{4}$

$b_4=\frac{a^2}{8}$

$b_5=\frac{a^2}{16}$

$b_6=\frac{a^2}{32}$

$...$

Ciąg liczb określających pola kolejnych kwadratów

$a^2$, $\frac{a^2}{2}$, $\frac{a^2}{4}$, $\frac{a^2}{8}$, $\frac{a^2}{16}$, $\frac{a^2}{32}$, $...$, $\frac{a^2}{2^{n-1}}$, $...$

stanowi ciąg geometrycznyciąg geometrycznyciąg geometryczny nieskończony o pierwszym wyrazie $a^2$ i ilorazie $q=\frac{1}{2}$.

Wnioskujemy, że wzór ogólny ciągu $\left(b_n\right)$ można zapisać w postaci

$b_n=\frac{a^2}{2^{n-1}}$

Obliczamy pole dziesiątego z tak otrzymanych kwadratów.

$b_{10}=\frac{a^2}{2^9}=\frac{a^2}{512}$

Odpowiedź:

Długość boku dziesiątego kwadratu jest równa $\frac{a}{16\sqrt{2}}$, a pole $\frac{a^2}{512}$.

Spirala (patrz rysunek) składa się z siedmiu półokręgów o średnicach odpowiednio równych $250$, $150$, $90$, $54$, $...$

RNLwz4LeQ8Fgv

Ilustracja przedstawia spiralę w układzie współrzędnych, której początek znajduje się na ujemnej półosi O X. Spirala zawija się w prawo i dąży do początku układu współrzędnych.

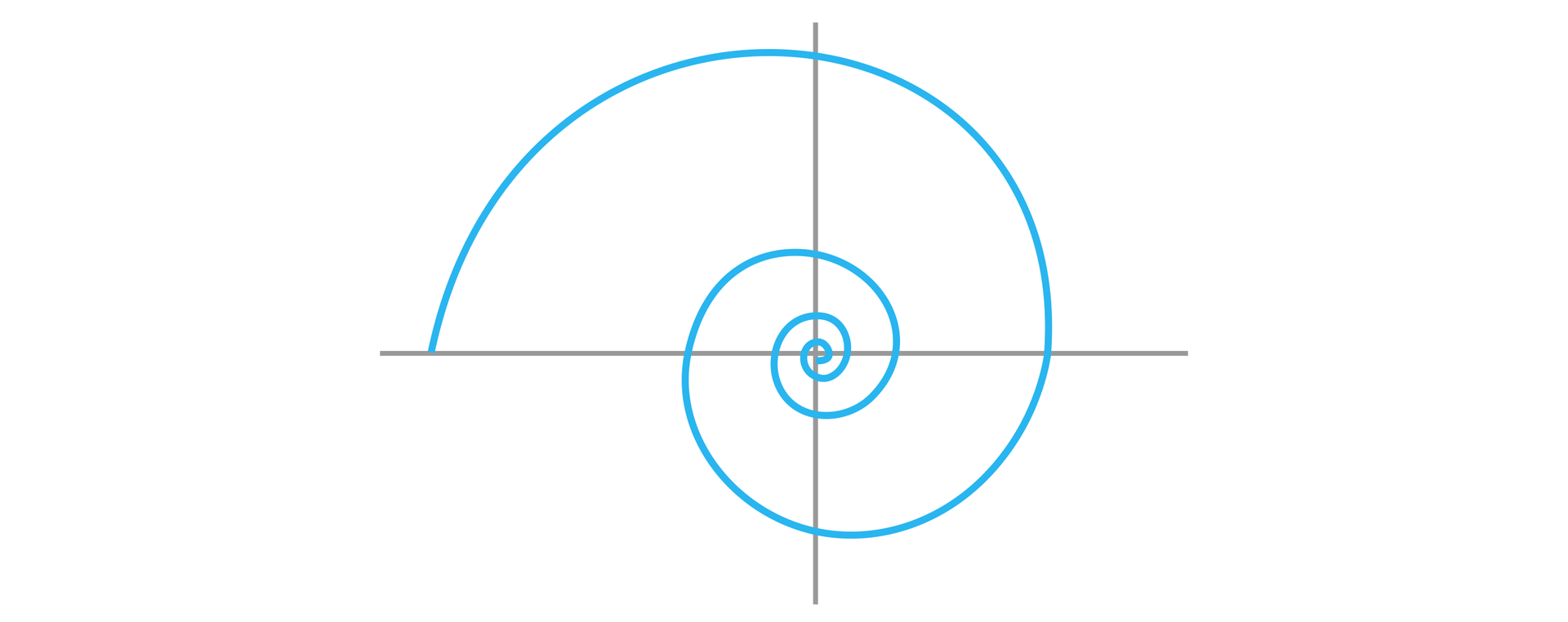
Obliczymy długość tej spirali.

Zauważmy, że długości średnic półokręgów, z których składa się spirala, tworzą siedmiowyrazowy ciąg geometryczny o pierwszym wyrazie równym $250$ i ilorazie $\frac{150}{250}=\frac{3}{5}$.

Zatem i długości półokręgów, z których zbudowana jest spirala, będą tworzyły pewien ciąg geometrycznyciąg geometrycznyciąg geometryczny, oznaczmy go $\left(d_n\right)$.

Przy czym pierwszy wyraz tego ciągu będzie równy $\frac{250\pi }{2}=125\pi$, a iloraz będzie nadal równy $\frac{3}{5}$.

Obliczymy kolejne wyrazy ciągu $\left(d_n\right)$.

$d_1=125\pi$

$d_2=\frac{3}{5}·125\pi =75\pi$

$d_3=\frac{3}{5}·75\pi =45\pi$

$d_4=\frac{3}{5}·45\pi =27\pi$

$d_5=\frac{3}{5}·27\pi =16,2\pi$

$d_6=\frac{3}{5}·16,2\pi =9,72\pi$

$d_7=\frac{3}{5}·9,72\pi =5,832\pi$

Długość spirali wynosi:

$125\pi +75\pi +45\pi +27\pi +\mathrm{16,2}\pi +\mathrm{9,72}\pi +5,832\pi =303,752\pi$.

Dany jest trójkąt równoboczny $T_1$ o boku długości $a$. Rysujemy kolejno trójkąty równoboczne $T_2$, $T_3$, $T_4$, $...$ tak, że długość boku kolejnego trójkąta jest równa wysokości poprzedniego trójkąta. Obliczymy pole dziesiątego tak utworzonego trójkąta.

Rr8DfIZlm6yvc

Ilustracja przedstawia trzy trójkąty równoboczne: T 1, T 2, T trzy. Trójkąty mają wspólny górny wierzchołek. Trójkąt T 1 ma bok a i wysokość h 1, trójkąt T 2 ma bok o długości h 1 i wysokość o długości h 2, trójkąt T 3 ma bok o długości h dwa.

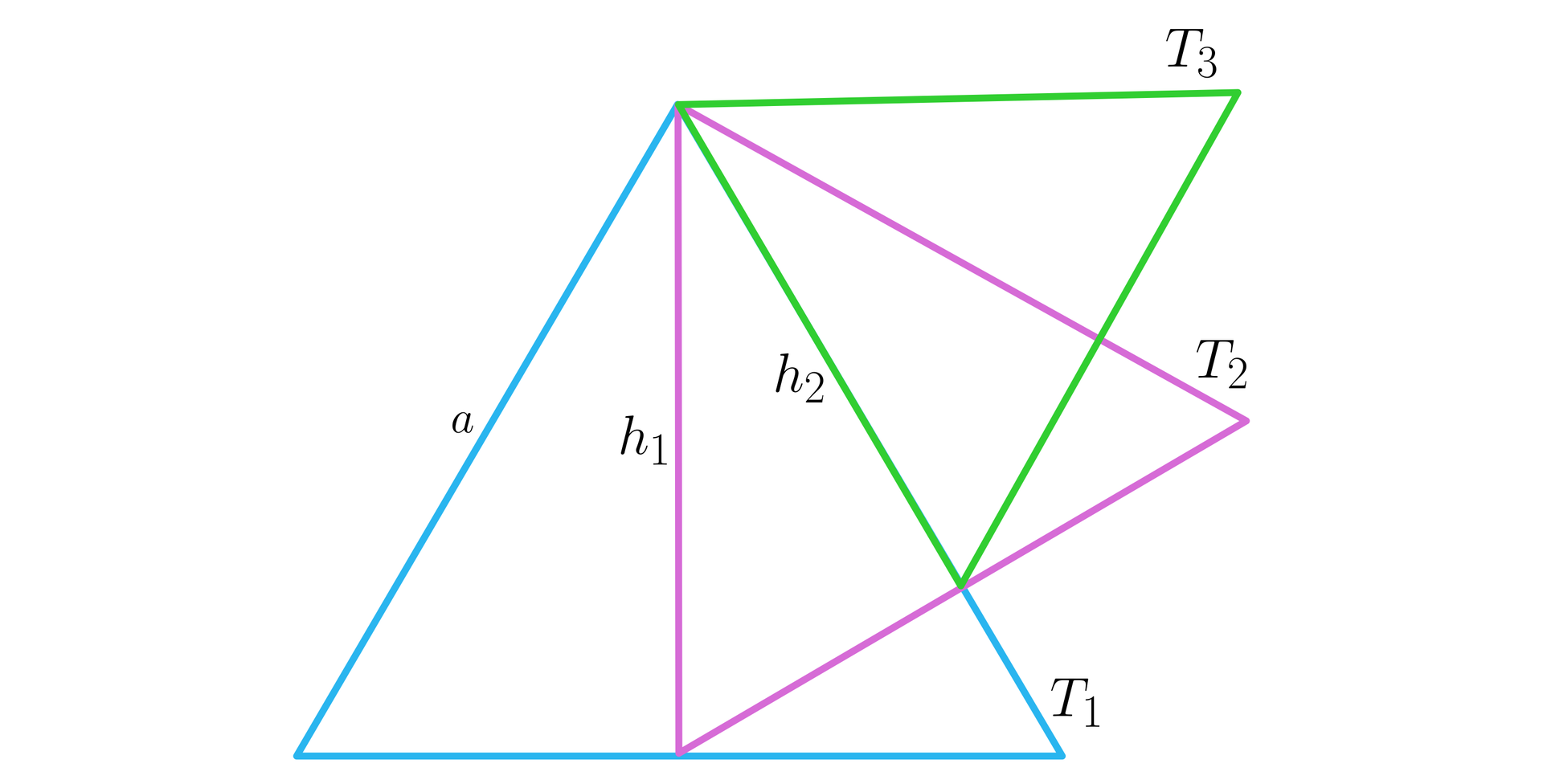
Aby obliczyć długości boków kolejnych trójkątów, korzystamy ze wzoru na wysokość trójkąta równobocznego o boku $a$: $h=\frac{a\sqrt{3}}{2}$.

Oznaczmy:
$a_1$, $a_2$, $a_3$, $...$ – długości boków kolejnych trójkątów,
$h_1$, $h_2$, $h_3$, $...$ – wysokości kolejnych trójkątów.

Wtedy:

$a_1=a$

$a_2=h_1=\frac{a\sqrt{3}}{2}$

$a_3=h_2=\frac{a\sqrt{3}}{2}·\frac{\sqrt{3}}{2}=\frac{3}{4}a$

$a_4=h_3=\frac{3}{4}a·\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{8}a$

$...$

Zauważmy, że długości boków kolejnych trójkątów tworzą ciąg geometryczny o pierwszym wyrazie $a$ i ilorazie $q=\frac{\sqrt{3}}{2}$.

Obliczamy długość boku trójkąta $T_{10}$.

$a_{10}=a·{\left(\frac{\sqrt{3}}{2}\right)}^9$

Korzystając ze wzoru na pole trójkąta równobocznego, obliczamy pole trójkąta $T_{10}$.

$P_{10}=\frac{\sqrt{3}}{4}·{\left[a·{\left(\frac{\sqrt{3}}{2}\right)}^9\right]}^2=\frac{\sqrt{3}}{4}·{\left(\frac{3}{4}\right)}^9·a^2$

$P_{10}=\frac{19683\sqrt{3}}{1048576}·a^2$

Odpowiedź:

Pole dziesiątego trójkąta jest równe $\frac{19683\sqrt{3}}{1048576}·a^2$.

ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$, zwaną ilorazem ciągu