Przeczytaj

Ciąg geometryczny jest pewną funkcją, której dziedziną jest podzbiór zbioru liczb naturalnych lub zbiór liczb naturalnych. Zatem definicje określające monotoniczność ciągu geometrycznego i sposoby określania tej monotoniczności, są analogiczne jak dla funkcji liczbowych.

Ciąg geometryczny rosnącyciąg geometryczny rosnącyCiąg geometryczny rosnący

R1HGUORI2BJfY

Ilustracja przedstawia interpretację graficzną ciągu an w układzie współrzędnych z poziomą osią n od minus dwóch do czterech i z pionową osią an od minus dwóch do ośmiu. Kolejne wyrazy ciągu to punkty o następujących współrzędnych: 0;1, 1;2, 2;4, 3;8.

Na wykresie zaznaczonych jest kilka początkowych wyrazów ciągu $(a_{n})$ , określonego wzorem ogólnym

a_{n} = 2^{n}

gdzie $n \in \{0, 1, 2, 3, \dots\}$ .

Zauważmy, że każdy wyraz ciągu (oprócz wyrazu pierwszego) jest większy od poprzedniego. O takim ciągu mówimy, że jest rosnącyciąg geometryczny rosnącyrosnący.

Poniżej przykłady jeszcze kilku ciągów geometrycznych rosnących.

3, 9, 27, 81, 243, \dots

\frac{1}{6}, \frac{2}{6}, \frac{4}{6}, \frac{8}{6}, \frac{16}{6}, \dots

10, 100, 1000, 10000, \dots

- 20; - 10; - 5; - 2, 5; - 1, 25; \dots

- 125, - 25, - 5, - 1, \dots

Zauważmy, że jeśli pierwszy wyraz ciągu geometrycznego rosnącego jest dodatni, to iloraz ciągu jest większy od $1$ . Natomiast, jeśli pierwszy wyraz ciągu jest ujemny, to iloraz ciągu musi być dodatni, ale mniejszy od $1$ .

Ciąg geometryczny rosnący

Twierdzenie: Ciąg geometryczny rosnący

Niech $(a_{n})$ będzie ciągiem geometrycznym o ilorazie $q$ .

Ciąg ten jest ciągiem rosnącym, gdy:

$a_{1} > 0$ i $q > 1$
lub

$a_{1} < 0$ i $0 < q < 1$

Przykład 1

Wykażemy, że ciąg geometryczny $(a_{n})$ określony wzorem $a_{n} = 2 \cdot 3^{n}$ , gdzie $n \in ℕ_{+}$ , jest rosnący.

Aby wykazać, że ciąg jest rosnący, należy zbadać różnicę $a_{n + 1} - a_{n}$ (dla dowolnego $n \geq 1$ ).

$a_{n + 1} - a_{n} = 2 \cdot 3^{n + 1} - 2 \cdot 3^{n}$

Przekształcamy otrzymane wyrażenie, korzystając z własności potęgowania.

$a_{n + 1} - a_{n} = 6 \cdot 3^{n} - 2 \cdot 3^{n} = 4 \cdot 3^{n}$

Zarówno liczba $4$ , jak i liczba $3^{n}$ $(n \geq 1)$ to liczby dodatnie. Iloczyn liczb dodatnich jest liczbą dodatnią.

$a_{n + 1} - a_{n} = 4 \cdot 3^{n} > 0$

Pokazaliśmy, że dla każdej liczby naturalnej $n \geq 1$ spełniony jest warunek $a_{n + 1} > a_{n}$ , co oznacza, że ciąg $(a_{n})$ jest rosnący.

Przykład 2

Znajdziemy takie liczby $x$ , $y$ , dla których ciąg $(16, x, 100, y)$ jest ciągiem geometrycznym rosnącym.

Niech $q$ będzie ilorazem rozpatrywanego ciągu.

Wtedy:
$16$ – pierwszy wyraz ciągu,
$x = 16 q$ – drugi wyraz ciągu,
$100 = 16 q^{2}$ – trzeci wyraz ciągu,
$y = 16 q^{3}$ – czwarty wyraz ciągu.

Wyznaczamy iloraz rozpatrywanego ciągu.

$100 = 16 q^{2}$

$q^{2} = \frac{100}{16} = \frac{25}{4}$

$q = \frac{5}{2}$ lub $q = - \frac{5}{2}$

Ciąg ma być rosnący, zatem tylko $q = \frac{5}{2}$ spełnia warunki zadania.

$x = 16 \cdot \frac{5}{2} = 40$

$y = 16 \cdot {(\frac{5}{2})}^{3} = \frac{16 \cdot 125}{8} = 250$

Odpowiedź:

Szukane liczby to $x = 40$ , $y = 250$ .

Ciąg geometryczny malejącyciąg geometryczny malejącyCiąg geometryczny malejący

Rmk1W58u1axWN

Ilustracja przedstawia interpretację graficzną ciągu an w układzie współrzędnych z poziomą osią n od minus dwóch do ośmiu i z pionową osią an od minus jeden do ośmiu. Kolejne wyrazy ciągu to punkty o następujących współrzędnych: 2;8, 3;4, 4;2, 5;1, 6;12, 7;14.

Na wykresie zaznaczonych jest kilka wyrazów ciągu $(a_{n})$ , określonego wzorem ogólnym

a_{n} = 8 \cdot {(\frac{1}{2})}^{n - 2}

gdzie $n \in \{2, 3, 4, \dots\}$ .

Zauważmy, że każdy wyraz ciągu (oprócz wyrazu pierwszego) jest mniejszy od poprzedniego. O takim ciągu mówimy, że jest malejącyciąg geometryczny malejącymalejący.

Poniżej przykłady jeszcze kilku ciągów geometrycznych malejących.

243, 81, 27, 9, 3, \dots

\frac{16}{6}, \frac{8}{6}, \frac{4}{6}, \frac{2}{6}, \frac{1}{6}, \dots

10000, 1000, 100, 10, 1, \dots

- 1, 25; - 2, 5; - 5; - 10; - 20; \dots

- 1, - 5, - 25, - 125, \dots

Zauważmy, że jeśli pierwszy wyraz ciągu geometrycznego malejącego jest ujemny, to iloraz ciągu jest większy od $1$ . Natomiast, jeśli pierwszy wyraz ciągu jest dodatni, to iloraz ciągu musi być dodatni, ale mniejszy od $1$ .

Ciąg geometryczny malejący

Twierdzenie: Ciąg geometryczny malejący

Niech $(a_{n})$ będzie ciągiem geometrycznym o ilorazie $q$ .

Ciąg ten jest ciągiem malejącym, gdy:

$a_{1} > 0$ i $0 < q < 1$
lub

$a_{1} < 0$ i $q > 1$

Przykład 3

Określimy dla jakim wartości parametru $k$ ( $k \neq 0$ i $k \neq \sqrt{6}$ ) ciąg geometryczny $(a_{n})$ określony wzorem ogólnym $a_{n} = (\sqrt{6} - k) \cdot {(k - 2)}^{n - 1}$ , gdzie $n \in \{1, 2, 3, 4, \dots\}$ jest malejący.

Zauważmy, że pierwszy wyraz rozpatrywanego ciągu $(a_{n})$ to $a_{1} = \sqrt{6} - k$ .

Natomiast iloraz ciągu to $q = k - 2$ .

Korzystając z twierdzenia o ciągu geometrycznym malejącym, rozpatrzymy dwa przypadki.

$a_{1} > 0$ i $0 < q < 1$
$\sqrt{6} - k > 0$ i $0 < k - 2 < 1$
$k < \sqrt{6}$ i $2 < k < 3$
Określamy część wspólną wszystkich warunków, jakie musi spełniać parametr $k$ .
$\{\begin{cases} k < \sqrt{6} \\ 2 < k < 3 \\ k \neq 0 \\ k \neq \sqrt{6} \end{cases}$
Otrzymujemy: $2 < k < \sqrt{6}$ .
$a_{1} < 0$ i $q > 1$
$\sqrt{6} - k < 0$ i $k - 2 > 1$
$k > \sqrt{6}$ i $k > 3$
Określamy część wspólną wszystkich warunków, jakie musi spełniać parametr $k$ .
$\{\begin{cases} k > \sqrt{6} \\ k > 3 \\ k \neq 0 \\ k \neq \sqrt{6} \end{cases}$
Otrzymujemy: $k > 3$ .

Z obu rozpatrywanych warunków wynika, że $k \in (2, \sqrt{6}) \cup (3, \infty)$ .

Odpowiedź:

Ciąg geometryczny $(a_{n})$ jest ciągiem malejącym dla $k \in (2, \sqrt{6}) \cup (3, \infty)$ .

Przykład 4

Liczby $x$ , $y$ , $w$ , $z$ (w tej kolejności) tworzą ciąg geometryczny malejący. Iloczyn logarytmów dziesiętnych pierwszej i czwartej z tych liczb jest równy $(- 8)$ . Iloczyn logarytmów dziesiętnych drugiej i trzeciej z tych liczb jest równy $0$ . Znajdziemy te liczby.

Oznaczmy przez $q$ iloraz ciągu $(x, y, w, z)$ .

Wtedy:
$y = x q$
$w = x q^{2}$
$z = x q^{3}$

Aby istniały logarytmy dziesiętne liczb $x$ , $y$ , $w$ , $z$ , każda z tych liczb musi być dodatnia. Zatem:

$x > 0$

$y > 0 \Rightarrow x q > 0 \Rightarrow q > 0$

$w > 0$

$z > 0$

Zapiszemy pierwszą z zależności między podanymi liczbami, wynikającą z treści zadania: iloczyn logarytmów dziesiętnych pierwszej i czwartej z tych liczb jest równy $(- 8)$ , czyli:

$\log x \cdot \log (x q^{3}) = - 8 (1)$

Z treści zadania ponad to wynika, że iloczyn logarytmów dziesiętnych drugiej i trzeciej z tych liczb jest równy $0$ . Stąd:

$\log (x q) \cdot \log (x q^{2}) = 0 (2)$

Z własności iloczynu wynika, że:

$\log (x q) = 0$ lub $\log (x q^{2}) = 0$ .

Rozpatrzymy więc dwie możliwości.

1 możliwość: $\log (x q) = 0$

Ponieważ $0 = \log 1$ , więc

$\log (x q) = \log 1$

$x q = 1 | : q$ ( $q \neq 0$ , bo $q > 0$ )

$x = \frac{1}{q}$

Podstawiamy wyznaczone $x$ do $(1)$ .

$\log x \cdot \log (x q^{3}) = - 8$

$\log \frac{1}{q} \cdot \log (\frac{1}{q} \cdot q^{3}) = - 8$

Przekształcamy otrzymane wyrażenie, korzystając z własności logarytmów.

$- \log q \cdot 2 \log q = - 8$

$\log^{2} q = 4$

Wyznaczamy z otrzymanego równania kwadratowego $q$ .

$\log q = 2$ lub $\log q = - 2$

$\log q = \log 100$ lub $\log q = \log \frac{1}{100}$

$q = 100$ lub $q = \frac{1}{100}$

Wyznaczamy $x$ i pozostałe wyrazy ciągu dla obu znalezionych wartości $q$ .

$q = 100 \Rightarrow x = \frac{1}{100}$
$y = 1$
$w = 100$
$z = 10000$
Każda z otrzymanych liczb jest dodatnia, ale ciąg $(\frac{1}{100}, 1, 100, 10000)$ jest rosnący, nie spełnia więc warunków zadania.
$q = \frac{1}{100}$
$x = 100$
$y = 1$
$w = \frac{1}{100}$
$z = \frac{1}{10000}$
Każda z otrzymanych liczb jest dodatnia i ciąg $(100, 1, \frac{1}{100}, \frac{1}{10000})$ jest ciągiem malejącym, spełnia więc warunki zadania.

2 możliwość: $\log (x q^{2}) = 0$ .

Postępujemy podobnie, jak poprzednio. Wyznaczamy $x$ i podstawiamy do $(1)$ .

$\log (x q^{2}) = \log 1$

$x q^{2} = 1$

$x = \frac{1}{q^{2}}$ ( $q \neq 0$ )

$\log x \cdot \log (x q^{3}) = - 8$

$\log \frac{1}{q^{2}} \cdot \log (\frac{1}{q^{2}} \cdot q^{3}) = - 8$

Korzystamy z własności logarytmu potęgi.

$- 2 \log q \cdot \log q = - 8$

$\log^{2} q = 4$

$\log q = 2$ lub $\log q = - 2$

Otrzymaliśmy do rozwiązania dokładnie te same równania, co w $1$ możliwości. Jednak rozwiązanie jest inne.

Jeśli $\log q = 2$ to $q = 100$ i $x = \frac{1}{10000}$ . Ciąg jest wtedy rosnący, więc nie spełnia warunków zadania.

Jeśli Jeśli $\log q = - 2$ to $q = \frac{1}{100}$ i $x = 10000$ . Wtedy

$y = \frac{1}{100} \cdot 10000 = 100$
$w = \frac{1}{100} \cdot 100 = 1$
$z = \frac{1}{100} \cdot 1 = \frac{1}{100}$ .

Odpowiedź:

Szukane liczby to:
$x = 100$ , $y = 1$ , $w = \frac{1}{100}$ , $z = \frac{1}{10000}$
lub
$x = 10000$ , $y = 100$ , $w = 1$ , $z = \frac{1}{100}$ .

Ciąg geometryczny stały

RasFhJE5948Er

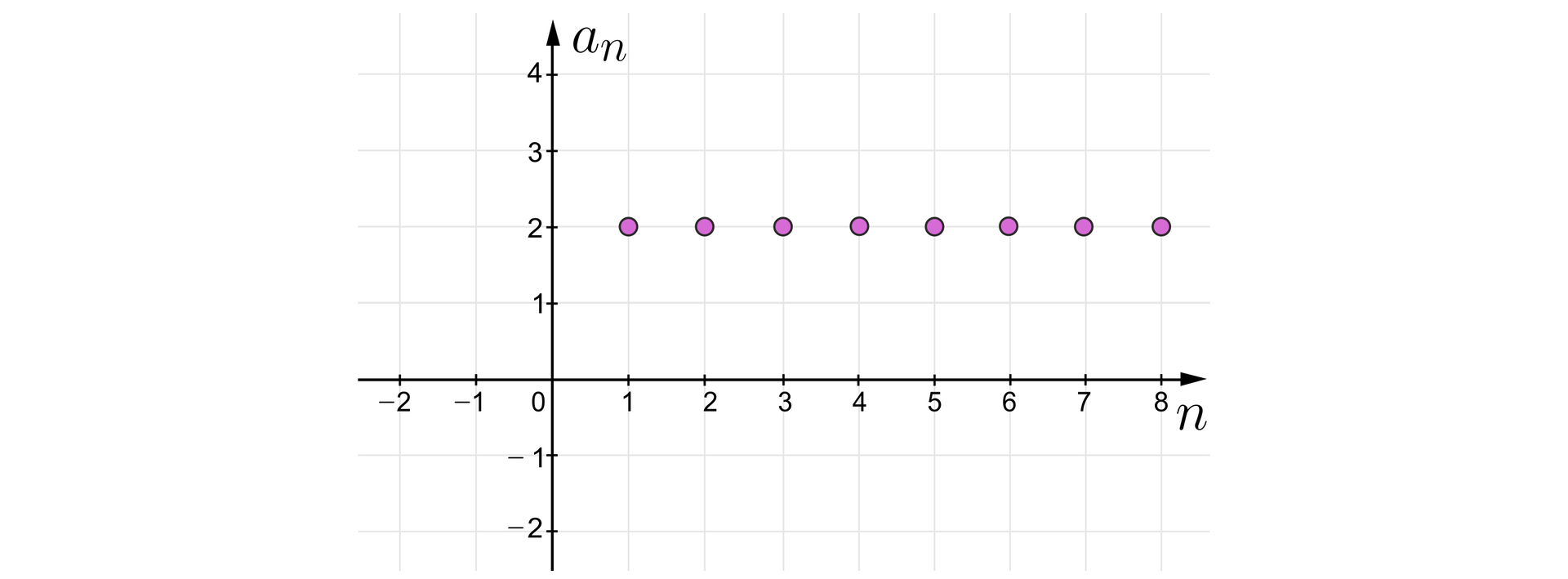
Na wykresie zaznaczonych jest kilka wyrazów ciągu $(a_{n})$ , określonego wzorem ogólnym

a_{n} = 2

gdzie $n \in \{1, 2, 3, \dots\}$ .

Zauważmy, że każdy wyraz ciągu ma tą samą wartość. O takim ciągu mówimy, że jest stały.

Poniżej przykłady jeszcze kilku ciągów geometrycznych stałych.

81, 81, 81, 81, \dots

\frac{16}{6}, \frac{16}{6}, \frac{16}{6}, \frac{16}{6}, \frac{16}{6}, \dots

0, 0, 0, 0, 0, \dots

- 10, - 10, - 10, - 10, \dots

Zauważmy, że iloraz ciągu geometrycznego stałego jest równy $1$ jeśli pierwszy wyraz ciągu jest różny od $0$ . Jeśli pierwszy wyraz ciągu geometrycznego stałego jest równy $0$ , to iloraz ciągu może być dowolną liczbą rzeczywistą.

Ciąg geometryczny stały

Twierdzenie: Ciąg geometryczny stały

Niech $(a_{n})$ będzie ciągiem geometrycznym o ilorazie $q$ .

Ciąg ten jest ciągiem stałym, gdy:

$a_{1} \neq 0$ i $q = 1$
lub

$a_{1} = 0$ i $q \in ℝ$

Ważne!

Zauważmy, że jeśli $a_{1} \neq 0$ i $q = 0$ to ciąg $(a_{n})$ jest stały, począwszy od drugiego wyrazu.

Ciąg stały nie jest ani rosnący, ani malejący.

Przykład 5

Znajdziemy taką liczbę $x$ , dla której ciąg $(x^{2}, x + 2, 6 - x)$ jest trzywyrazowym ciągiem stałym.

W ciągu stałym wszystkie wyrazy są równe, zatem:

$x + 2 = 6 - x$

$2 x = 4$

$x = 2$

Ciąg ma postać: $(4, 4, 4)$ .

Odpowiedź:

Szukana liczba to $2$ .

Ciąg geometryczny naprzemienny

RPQXJdtesjmBb

Ilustracja przedstawia interpretację graficzną ciągu an w układzie współrzędnych z poziomą osią n od minus jeden do trzynastu i z pionową osią an od minus czterech do pięciu. Kolejne wyrazy ciągu to punkty o następujących współrzędnych: 1;-14, 2;12, 3;-34, 4;1, 5;-54, 6;32, 7;-74, 8;2, 9;-114, 10;134, 11;-154, 12;194.

Nie każdy ciąg geometryczny jest monotoniczny. Fragment wykresu takiego ciągu przedstawia rysunek. Zauważmy, że wyrazy tego ciągu są na przemian dodatnie i ujemne. O takim ciągu mówimy, że jest naprzemienny.

Ważne!

Jeśli ciąg geometryczny $(a_{n})$ jest takim ciągiem, że $a_{1} \neq 0$ i $q < 0$ to ciąg ten jest ciągiem naprzemiennym, czyli wyrazy tego ciągu są na przemian dodatnie i ujemne.

Gdy $a_{1} > 0$ i $q < 0$ to wszystkie wyrazy o indeksach nieparzystych, ciągu $(a_{n})$ określonego wzorem ogólnym $a_{n} = a_{1} \cdot q^{n - 1}$ , są dodatnie, zaś wyrazy o indeksach parzystych są ujemne.

Gdy $a_{1} < 0$ i $q < 0$ to wszystkie wyrazy o indeksach nieparzystych, ciągu $(a_{n})$ określonego wzorem ogólnym $a_{n} = a_{1} \cdot q^{n - 1}$ , są ujemne, zaś wyrazy o indeksach parzystych są dodatnie.

Przykłady ciągów naprzemiennych:

- 5, 10, - 20, 40, \dots

4, - 4, 4, - 4, 4, - 4, \dots

- \frac{1}{2}, \frac{1}{4}, - \frac{1}{8}, \frac{1}{16}, \dots

Słownik

ciąg geometryczny rosnący

niech $(a_{n})$ będzie ciągiem geometrycznym o ilorazie $q$ ; ciąg ten jest ciągiem rosnącym, gdy:

$a_{1} > 0$ i $q > 1$
lub

$a_{1} < 0$ i $0 < q < 1$

ciąg geometryczny malejący

niech $(a_{n})$ będzie ciągiem geometrycznym o ilorazie $q$ ; ciąg ten jest ciągiem malejącym, gdy:

$a_{1} > 0$ i $0 < q < 1$
lub

$a_{1} < 0$ i $q > 1$

Wprowadzenie

Aplet

Ciąg geometryczny rosnącyciąg geometryczny rosnącyCiąg geometryczny rosnący

Ciąg geometryczny malejącyciąg geometryczny malejącyCiąg geometryczny malejący

Ciąg geometryczny stały

Ciąg geometryczny naprzemienny

Słownik