Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego definiujemy jako sumę pól jego podstaw i pola powierzchni bocznej. Wobec tego pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe polu jego siatkisiatka graniastosłupa prawidłowego czworokątnegosiatki. Zależność tę opisuje wzór:

gdzie:
$h$ – jest długością wysokości graniastosłupa prawidłowego czworokątnego,
$a$ – jest długością krawędzi podstawy graniastosłupa prawidłowego czworokątnego.

R1GhKdXSnAwDX

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o bokach długości $a$, $a$, $h$. Obok przedstawiono siatkę graniastosłupa, składającą się z czterech prostokątów o polu powierzchni $a\times h$, oraz dwóch podstaw o powierzchni $a^2$.

W graniastosłupie prawidłowym czworokątnym $ABCDEFGH$ przedstawionym na poniższym rysunku wysokość $h$ jest o $2$ dłuższa od krawędzi podstawy $a$. Przekątna $D$ tego graniastosłupa tworzy z przekątną $d$ ściany bocznej kąt $\alpha$ taki, że $\mathrm{tg}\alpha =0,6$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

R1JyGhq365QkW

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o podstawie dolnej $ABCD$, oraz górnej $EFGH$. Zaznaczono kąt alfa między przekątną $BG$ ściany bocznej, a przekątną $AG$ graniastosłupa.

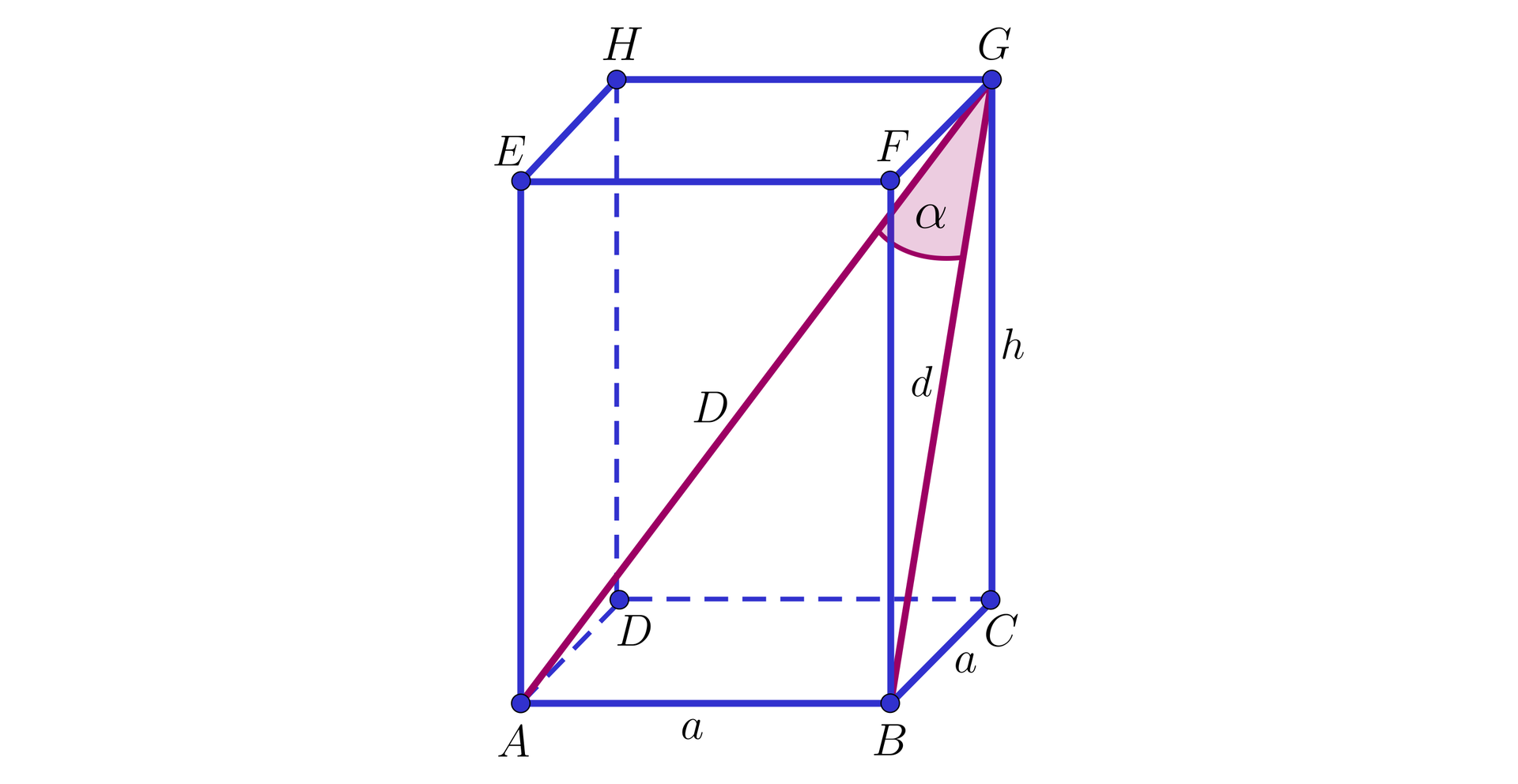
Rozwiązanie:

Z treści zadania wynika, że $h=a+2$. Z trójkąta $ABG$ mamy:

$\mathrm{tg}\alpha =\frac{a}{d}=0,6$, a stąd $a=0,6d$.

Z twierdzenia Pitagorasa dla trójkąta $BCG$ mamy:

$d^2={\left(a+2\right)}^2+a^2=2a^2+4a+4$.

Po podstawieniu zależności $a=0,6d$, wykonaniu działań oraz redukcji wyrazów podobnych otrzymujemy równanie:

$7d^2-60d-100=0$.

Wyróżnik równania wynosi $∆={\left(-60\right)}^2-4·7·\left(-100\right)=6400$.

Otrzymujemy następujące rozwiązania: $d=\frac{-10}{7}<0$ lub $d=10$. Stąd wynika, że $a=0,6d=6$ oraz $h=a+2=8$.

Obliczymy teraz pole powierzchni całkowitej graniastosłupa

$P_c=2a^2+4ah=2\cdot 36+4\cdot 6\cdot 8=264$.

W graniastosłupie prawidłowym czworokątnym $ABCDEFGH$ przedstawionym na poniższym rysunku stosunek długości wysokości $h$ do długości krawędzi podstawy $a$ wynosi $2$. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem ostrym, którego tangens wynosi $2\sqrt{2}$. Pole otrzymanego przekroju wynosi $24$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

RnLmIWDXlwloe

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o podstawie dolnej $ABCD$, oraz górnej $EFGH$. Na krawędzi bocznej $BF$ zaznaczono punkt P. Zaznaczono trójkąt równoramienny $APC$. Z wierzchołka P opuszczono wysokość trójkąta do podstawy $AC$, do punktu S, stanowiącego punkt przecięcia przekątnych podstawy graniastosłupa. $\angle PSB$ oznaczono alfa.

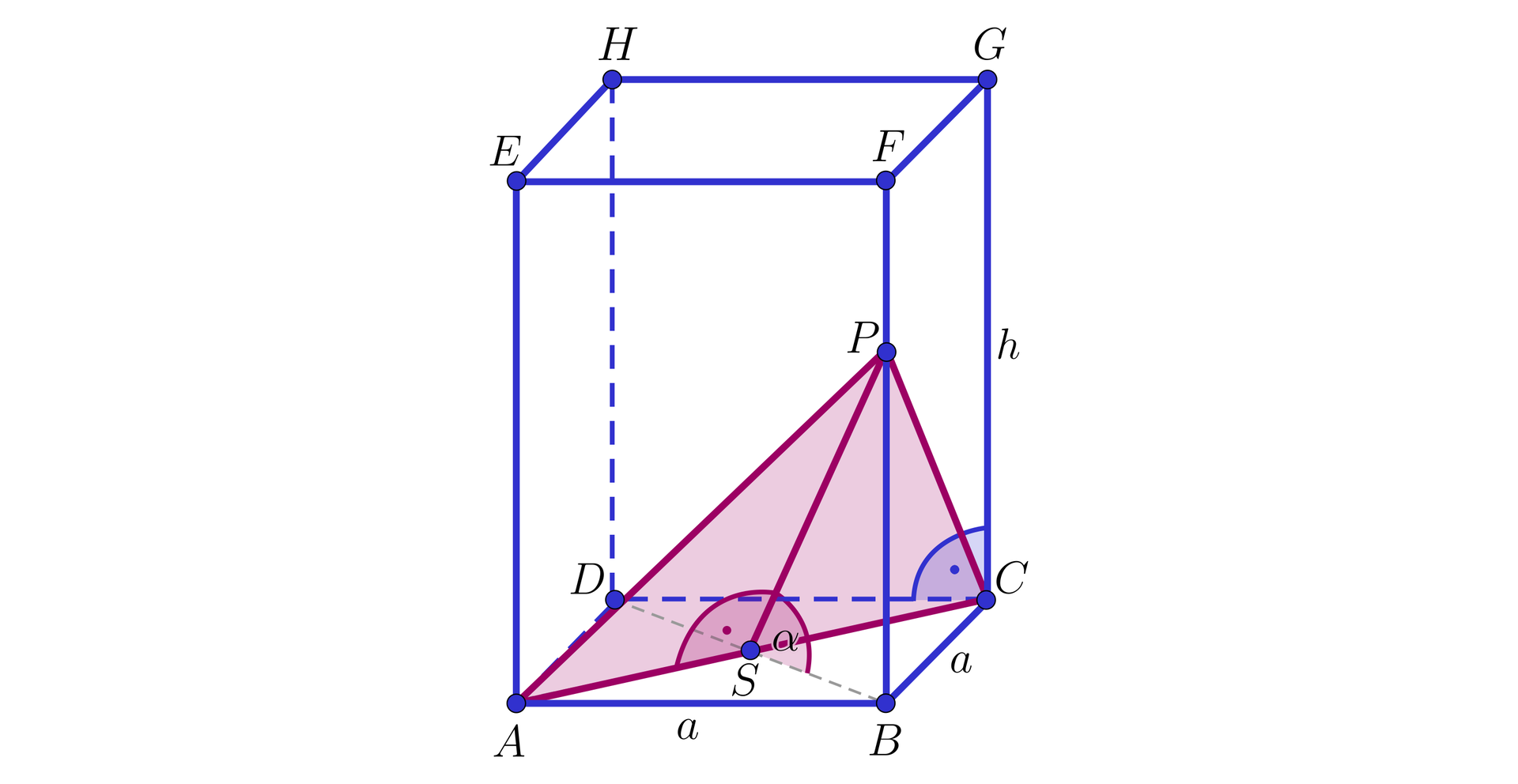
Rozwiązanie:

Przekrój $APC$ jest trójkątem równoramiennym. Jego podstawą jest odcinek $\left|AC\right|=a\sqrt{2}$, a wysokością odcinek $\left|PS\right|$. Pole przekroju graniastosłupa obliczymy zatem ze wzoru $P_{ACP}=\frac{1}{2}·a\sqrt{2}·\left|PS\right|$.

Wyznaczymy zależność wysokości $\left|PS\right|$ od długości krawędzi graniastosłupa $a$ z trójkąta prostokątnego $PBS$:

$\cos \alpha =\frac{\left|SB\right|}{\left|PS\right|}$.

Stąd otrzymujemy, że $\left|PS\right|=\frac{\left|SB\right|}{\cos \alpha }=\frac{a\sqrt{2}}{2\cos \alpha }$.

Wiemy, że $\mathrm{tg}\alpha =2\sqrt{2}$.

Stąd $\mathrm{t}\mathrm{g}\alpha =\frac{\sin \alpha }{\cos \alpha }=2\sqrt{2}$, czyli $\sin \alpha =2\sqrt{2}\cos \alpha$.

Podstawiając tę zależność do jedynki trygonometrycznejjedynka trygonometrycznajedynki trygonometrycznej otrzymujemy:

$8{\cos }^2\alpha +{\cos }^2\alpha =1$, co daje: $\cos \alpha =\frac{1}{3}$.

Możemy obliczyć wysokość trójkąta $APC$:

$\left|PS\right|=\frac{a\sqrt{2}}{2\cos \alpha }=\frac{3a\sqrt{2}}{2}$.

Podstawiamy tę zależność do wzoru na pole przekroju i otrzymujemy

$\frac{1}{2}·a\sqrt{2}·\frac{3a\sqrt{2}}{2}=24$.

Stąd wyliczamy długość krawędzi podstawy $a$ i wysokość $h$:

$\frac{3}{2}{a}^2=24$, czyli $a=4$

Wiemy, że $\frac{h}{a}=2$, zatem wysokość graniastosłupa $h=2a$, czyli: $h=8$.

Obliczymy pole powierzchni całkowitej graniastosłupa

$P_c=2a^2+4ah=2·16+4·4·8=160$.

W graniastosłupie prawidłowym czworokątnym $ABCDEFGH$ przedstawionym na poniższym rysunku połączono środki trzech krawędzi graniastosłupa, z których żadne dwie nie leżą w jednej płaszczyźnie i otrzymano trójkąt równoramienny $KLM$ o bokach długości $12$, $12$, $12\sqrt{2}$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

R17ctuw2pFvXa

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o podstawie dolnej $ABCD$, oraz górnej $EFGH$. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B, wierzchołek F i tak dalej. Punkt M jest środkiem krawędzi $EH$, punkt L jest środkiem krawędzi $GC$, punkt K jest środkiem krawędzi $AB$. Połączono punkty $KLM$ i otrzymano trójkąt równoramienny. Linią przerywaną połączono punkt M z wierzchołkiem G, punkt K z wierzchołkiem E, punkt K z wierzchołkiem C.

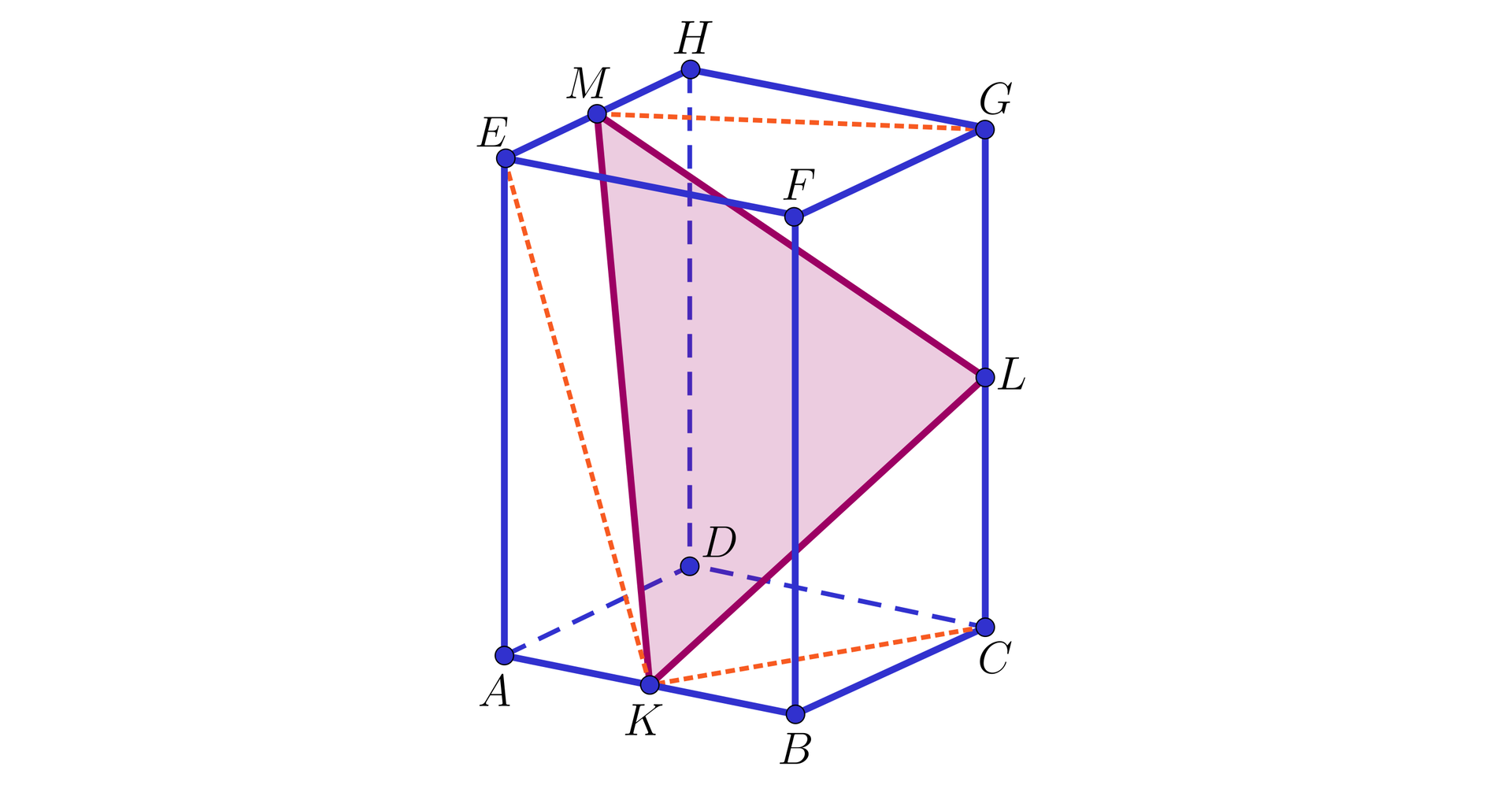
Rozwiązanie:

Niech $a$ oznacza długość krawędzi podstawy rozważanego graniastosłupa prawidłowego czworokątnego, $h$ oznacza długość jego wysokości.

Stosując twierdzenie Pitagorasa dla trójkątów $KBC$, $MHG$ oraz $EAK$ otrzymujemy

${\left|KC\right|}^2={\left|MG\right|}^2={\left(\frac{1}{2}a\right)}^2+a^2=\frac{5}{4}{a}^2$,

${\left|KE\right|}^2=h^2+{\left(\frac{1}{2}a\right)}^2=h^2+\frac{1}{4}{a}^2$.

Następnie stosujemy twierdzenie Pitagorasatwierdzenie Pitagorasatwierdzenie Pitagorasa dla trójkątów $KCL$, $KEM$, $MGL$ i jednocześnie podstawiamy otrzymane wcześniej wyniki. Mamy:

W $△KCL$:

${\left|KL\right|}^2={\left|KC\right|}^2+{\left|CL\right|}^2$

$\frac{5}{4}{a}^2+\frac{1}{4}{h}^2=144$

W $△KEM$:

${\left|KM\right|}^2={\left|EM\right|}^2+{\left|KE\right|}^2$

$h^2+\frac{1}{2}{a}^2=288$

W $△MGL$:

${\left|LM\right|}^2={\left|KL\right|}^2$

$\frac{5}{4}{a}^2+\frac{1}{4}{h}^2=144$

Otrzymujemy układ równań:

$\left\{\begin{array}{l}\frac{5}{4}{a}^2+\frac{1}{4}{h}^2=144\\ h^2+\frac{1}{2}{a}^2=288\end{array}\right.$

Rozwiązując układ, otrzymujemy

$\left\{\begin{array}{l}\frac{5}{4}{a}^2+\frac{1}{4}{h}^2=144 |·4\\ h^2+\frac{1}{2}{a}^2=288\end{array}\right.$

$\left\{\begin{array}{l}5a^2+h^2=576\\ h^2+\frac{1}{2}{a}^2=288\end{array}\right.$

$4,5a^2=288$

$a^2=64$

Stąd: $a=8$ oraz $h=16$.

Obliczamy pole powierzchni całkowitej graniastosłupa:

$P_{pc}=2a^2+4ah=2·64+4·8·16=640$.

W graniastosłupie prawidłowym czworokątnym $ABCDEFGH$ przedstawionym na poniższym rysunku o krawędzi podstawy długości $6$ poprowadzono płaszczyznę przechodzącą przez przekątną dolnej podstawy i wierzchołek górnej podstawy. Płaszczyzna ta wyznaczyła przekrój graniastosłupa, który jest trójkątem równoramiennym. Wiedząc, że na tym trójkącie można opisać okrąg o promieniu $5\sqrt{2}$ obliczymy pole powierzchni całkowitej tego graniastosłupa.

R16BYqTyFqKFF

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o podstawie dolnej $ABCD$, oraz górnej $EFGH$. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B, wierzchołek F i tak dalej. Połączono wierzchołki $ACH$, w taki sposób, że powstał trójkąt równoramienny. $\angle AHC$ oznaczono alfa.

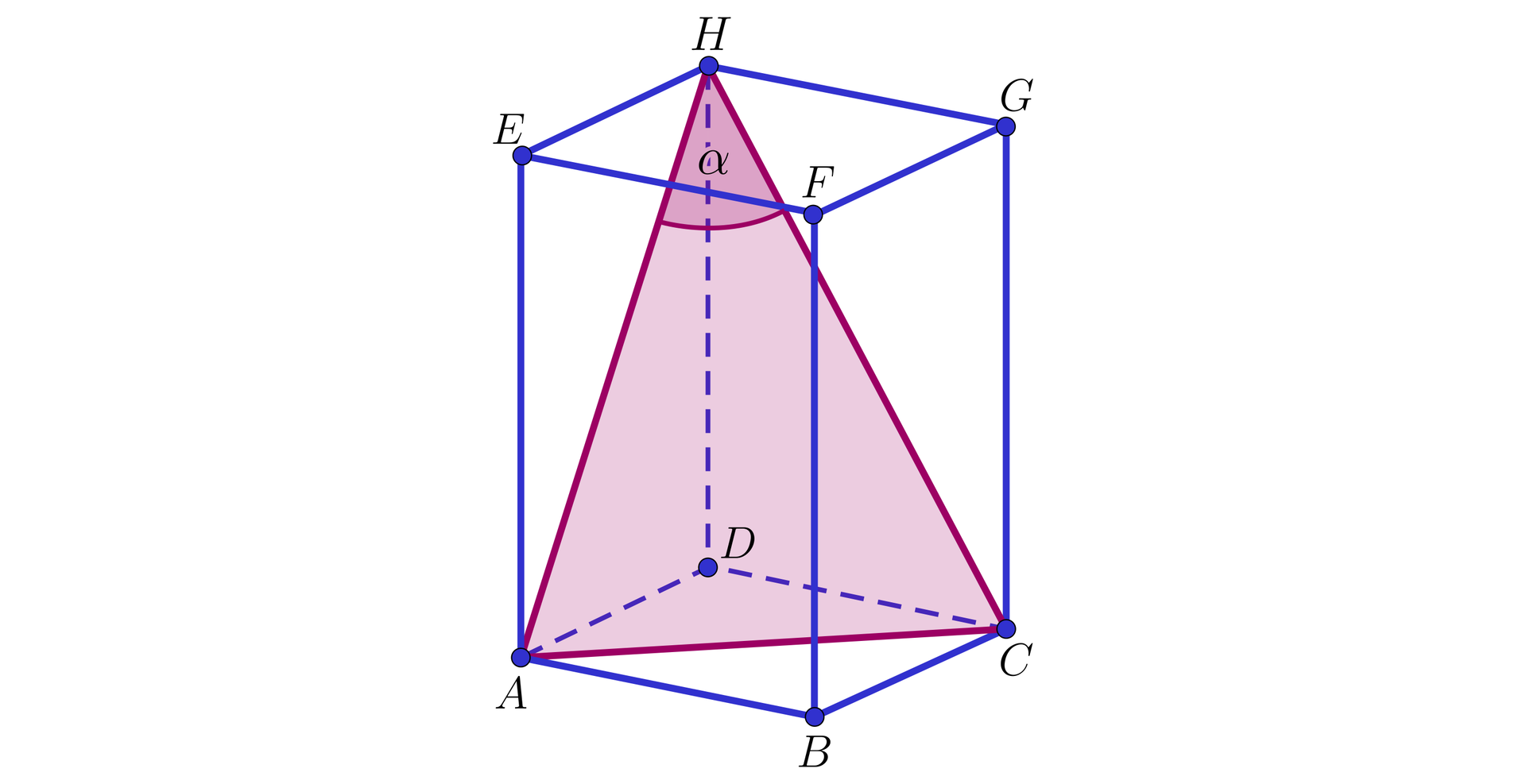
Rozwiązanie:

Przyjmijmy oznaczenia $\left|HC\right|=\left|AH\right|=d$ oraz $\sphericalangle AHC=\alpha$.

Z treści zadania mamy $\left|AB\right|=\left|BC\right|=6$, stąd przekątna podstawy $\left|AC\right|=6\sqrt{2}$.

Z twierdzenia sinusówtwierdzenie sinusówtwierdzenia sinusów dla trójkąta $ACH$ mamy:

$\frac{6\sqrt{2}}{2\sin \alpha }=5\sqrt{2}$, zatem $\frac{3}{\sin \alpha }=5$, stąd $\sin \alpha =0,6$.

Korzystając z jedynki trygonometrycznejjedynka trygonometrycznajedynki trygonometrycznej możemy wyliczyć wartość funkcji cosinus kąta $\alpha$. Mamy

$\cos \alpha =\sqrt{1-{\sin }^2\alpha }=\sqrt{1-0,36}=0,8$.

Zastosujemy twierdzenie cosinusówtwierdzenie Cosinusówtwierdzenie cosinusów do trójkąta $ACH$. Mamy

${\left(6\sqrt{2}\right)}^2=d^2+d^2-2·d·d·\cos \alpha$,

$72=2d^2-1,6d^2=0,4d^2$,

$d^2=180$,

$d=6\sqrt{5}$.

Stosując twierdzenie Pitagorasatwierdzenie Pitagorasatwierdzenie Pitagorasa do trójkąta $ABE$ otrzymujemy: $h=\sqrt{180-36}=12$.

Możemy obliczyć pole powierzchni całkowitej graniastosłupa

$P_c=2a^2+4ah=2·36+4·6·12=360$.

Z $n$ jednakowych sześcianów zbudowano graniastosłup prawidłowy czworokątnygraniastosłup prawidłowy czworokątnygraniastosłup prawidłowy czworokątny $ABCDEFGH$.

R1KpfRDiJIzy1

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o podstawie dolnej $ABCD$, oraz górnej $EFGH$. Nad wierzchołkiem A, B, C, D zaznaczono na krawędziach bocznych odpowiednio punkty A prim, B prim, C prim, D prim. Po połączeniu wierzchołków powstał sześcian o podstawie dolnej $ABCD$, oraz górnej A prim, B prim, C prim, D prim. Zaznaczono przekątną $AG$ graniastosłupa, oraz przekątną $AC\text{'}$ sześcianu. Zaznaczono kąt alfa między tymi przekątnymi.

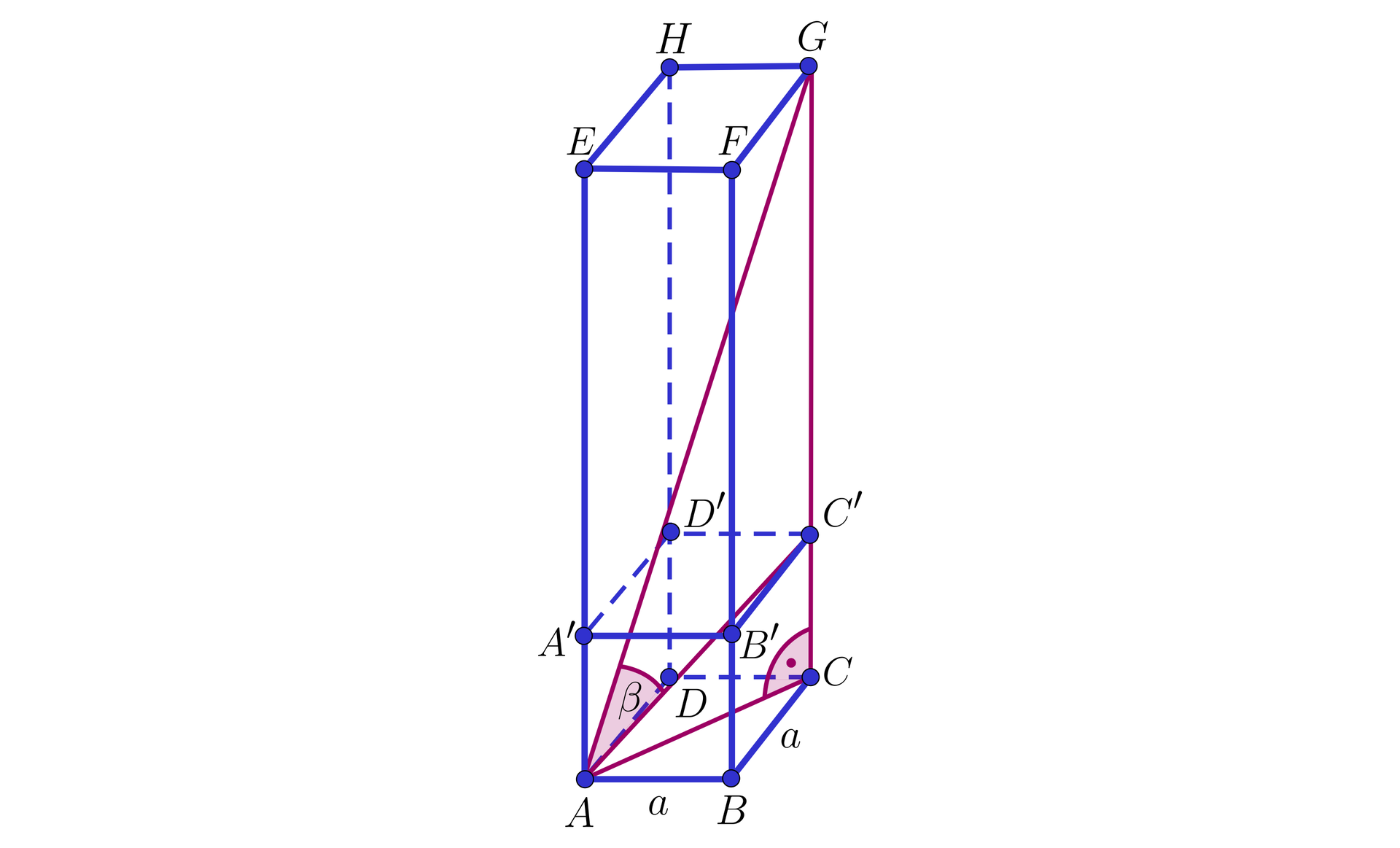
Przekątna tego graniastosłupa o długości $9$ tworzy z przekątną sześcianu $ABCDA\text{'}B\text{'}C\text{'}D\text{'}$ kąt, którego cosinus jest równy $\frac{7}{9}$. Obliczymy, z ilu sześcianów zbudowany jest graniastosłup oraz jakie jest jego pole powierzchni całkowitej.

Rozwiązanie:

Z treści zadania mamy $\left|AG\right|=d=9$ oraz $\cos \beta =\frac{7}{9}$.

Wprowadźmy oznaczenia: $\sphericalangle C\text{'}AC=\alpha$, $\left|AE\right|=\left|BF\right|=\left|CG\right|=\left|DH\right|=h=n·a$, $\left|CC\text{'}\right|=a$ oraz przekątna $AC\text{'}$ sześcianu o krawędzi $a$ ma długość $a\sqrt{3}$. Wynika stąd, że $\left|C\text{'}G\right|=\left(n-1\right)a$ oraz $\left|\sphericalangle GC\text{'}A\right|=90°+\alpha$.

Z jedynki trygonometrycznejjedynka trygonometrycznajedynki trygonometrycznej oraz wzoru redukcyjnego $\sin \left(90°+\alpha \right)=\cos \alpha$ otrzymujemy:

$\sin \beta =\sqrt{1-\frac{49}{81}}=\sqrt{\frac{32}{81}}=\frac{4\sqrt{2}}{9}$,

a w trójkącie $ACC\text{'}$:

$\sin \left(90°+\alpha \right)=\cos \alpha =\frac{a\sqrt{2}}{a\sqrt{3}}=\frac{\sqrt{6}}{3}$,

$\sin \alpha =\frac{a}{a\sqrt{3}}=\frac{\sqrt{3}}{3}$.

Zastosujemy twierdzenie sinusówtwierdzenie sinusówtwierdzenie sinusów w trójkącie $AC\text{'}G$. Mamy:

$\frac{9}{\sin \left(90°+\alpha \right)}=\frac{\left(n-1\right)a}{\sin \beta }$.

Podstawiając wyliczone wcześniej wartości funkcji trygonometrycznych otrzymujemy:

$\frac{9}{\frac{\sqrt{6}}{3}}=\frac{\left(n-1\right)a}{\frac{4\sqrt{2}}{9}}$,

$\left(n-1\right)a=\frac{9}{\frac{\sqrt{6}}{3}}·\frac{4\sqrt{2}}{9}$,

$\left(n-1\right)a=4\sqrt{3}$.

Zatem $\left|CG\right|=a+4\sqrt{3}$. Zastosujemy twierdzenie Pitagorasatwierdzenie Pitagorasatwierdzenie Pitagorasa do trójkąta $ACG$:

${\left(a\sqrt{2}\right)}^2+{\left(a+4\sqrt{3}\right)}^2=9^2$,

Po wykonaniu potęgowania oraz redukcji wyrazów podobnych otrzymujemy równanie kwadratowe:

$3a^2+8\sqrt{3}a-33=0$.

Wyróżnik równania wynosi $∆={\left(8\sqrt{3}\right)}^2-4·3·\left(-33\right)=3·196=588$.

Otrzymujemy następujące rozwiązania:

$a=\frac{-11\sqrt{3}}{3}<0$ (odrzucamy, bo jest ujemne) oraz $a=\sqrt{3}$.

Zatem $\left(n-1\right)\sqrt{3}=4\sqrt{3}$, skąd wynika, że $n=5$, czyli graniastosłup został zbudowany z $5$ jednakowych sześcianów.

Możemy wyliczyć wysokość $h$ graniastosłupa: $h=n·a=5\sqrt{3}$.

Obliczymy teraz pole powierzchni całkowitej graniastosłupa

$P_{pc}=2a^2+4ah=2·3+4·\sqrt{3}·5\sqrt{3}=66$.

graniastosłup prosty, którego podstawą jest kwadrat

przedstawienie graniastosłupa na płaszczyźnie w taki sposób, aby po wycięciu dało się złożyć jego model

w dowolnym trójkącie iloraz długości dowolnego boku i sinusa kąta naprzeciw tego boku jest stały i równy długości średnicy okręgu opisanego na tym trójkącie

w dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi

w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta

dla dowolnego kąta $\alpha$ zachodzi tożsamość