Przeczytaj
Przystawanie trójkątów w trapezie równoramiennym
Rozważmy trapeztrapez równoramienny niebędący równoległobokiem, w którym oraz , jak na rysunku.
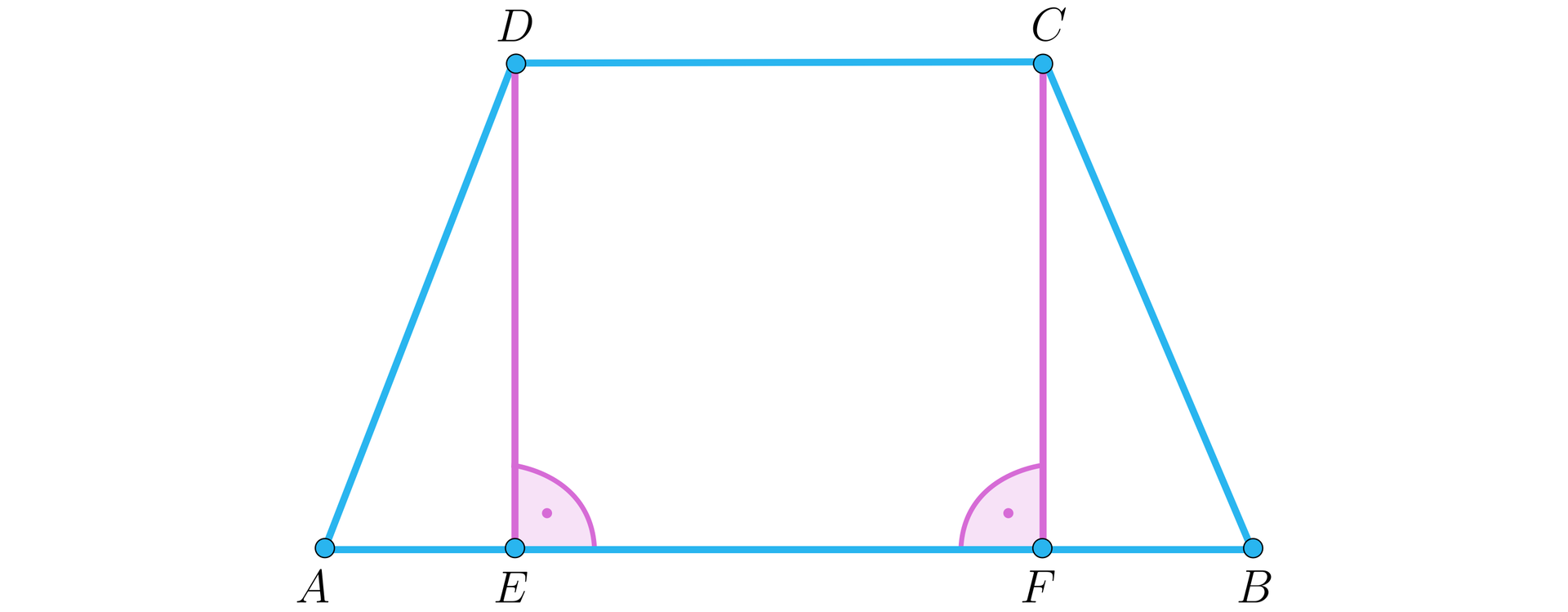
Przez punkty odpowiednio , leżące na podstawie , poprowadźmy odcinki oraz prostopadłe do tej podstawy. Wtedy czworokąt jest prostokątem i w szczególności oraz . Oczywiście odcinki , są wysokościami trapezu poprowadzonymi z wierzchołków odpowiednio oraz .
Udowodnimy teraz równość odcinków oraz , którą „łatwo widać” i zazwyczaj korzysta się z niej bez wcześniejszego udowodnienia. Zauważmy, że trójkąty oraz są trójkątami prostokątnymi, których przeciwprostokątne są równe (trapez równoramienny). Ponadto równe są przyprostokątne oraz . Zatem na mocy cechy przystawania trójkątówcechy przystawania trójkątów prostokątnych mamy, że . Oznacza to, że również odcinki oraz są równe. Ponadto, z faktu, że i wcześniej wskazanych równości wynika, że .
Pokażemy, korzystając z wykazanej wcześniej równości, że w trapezie równoramiennym, w którym dłuższa podstawa ma długość , a ramiona i krótsza podstawa mają długości , wysokość poprowadzona na dłuższą podstawę jest równa .
Przyjmijmy oznaczenia, jak na rysunku.
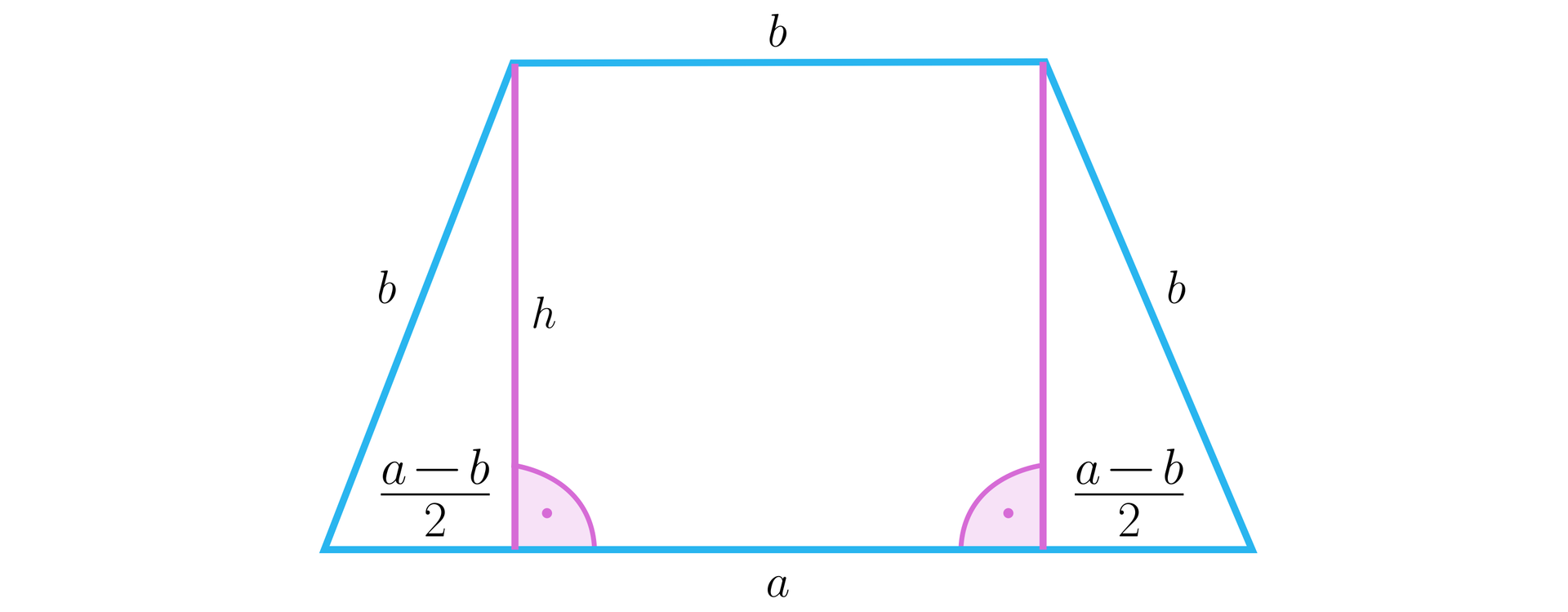
Z twierdzenia Pitagorasa mamy . Zatem
Stąd .
W okrąg o promieniu wpisano trapez , którego ramię ma długość , a podstawa jest średnicą tego okręgu, jak na rysunku.

Wyznaczymy pole tego trapezu.
Na początek udowodnimy, że . Przystawanie tych trójkątów pozwoli stwierdzić, że trapez ten jest równoramienny (jak każdy trapez wpisany w okrąg) – wówczas będziemy mogli skorzystać ze związków miarowych wyznaczonych wcześniej.
Trójkąty oraz są trójkątami prostokątnymi, gdyż każdy trójkąt, którego jednym z boków jest średnica okręgu na nim opisanego, jest prostokątny. Zauważmy, że kąty oraz , jako naprzemianległe, są równe. Ale kąt wpisany jest rozpięty na tym samym łuku, co kąt , zatem są one równe. Oznacza to, że trójkąty oraz mają równe kąty ostre i wspólną przeciwprostokątną, co na mocy cech przystawania trójkątów prostokątnych dowodzi, iż są one przystające. Przystawanie to oznacza w szczególności, że . Zatem trapez jest równoramienny.
Teraz przejdźmy do obliczeń. Zauważmy, że , zatem . Pole trójkąta jest więc równe . Pole to możemy wyrazić także jako . Stąd oraz . Czyli .
Skoro trapeztrapez jest równoramienny, to . Zauważmy ponadto, że , czyli odcinek ten jest równy linii środkowej trapezulinii środkowej trapezu. Pozostaje zauważyć, że ostatnia równość pozwala obliczyć krótszą podstawę trapezu, ale nie jest to konieczne, bo otrzymane wyrażenie możemy podstawić do wzoru na pole trapezu: .
Trójkąty przystające w równoległoboku
Jeśli w dowolnym równoległoboku poprowadzimy przekątne, to ich punkt przecięcia dzieli je na połowy. Fakt ten jest powszechnie wykorzystywany i zgodny z intuicją. W tym miejscu tę zależność udowodnimy. Przyjmijmy oznaczenia, jak na rysunku.

Zauważmy, że kąty i oraz i , jako naprzemianległe, są równe. Ponadto . Zatem na mocy cechy kąt‑bok‑kąt mamy, że . Stąd w szczególności oraz , co oznacza, że punkt dzieli przekątne oraz na połowy.
Pozostaje dodać, że otrzymane równości oraz , przy równości kątów wierzchołkowych, pozwalają stwierdzić, że również trójkąty oraz są przystające.
Jako wniosek warto podać, że punkt dzieli każdą z wysokości oraz tego równoległoboku na połowy, jak na rysunku.

Ostatnią własność wykorzystamy do rozwiązania poniższego problemu.
Odległości punktu przecięcia się przekątnych równoległoboku od jego boków i są równe odpowiednio i . Obwód tego równoległoboku jest równy . Oblicz pole równoległoboku.
Przyjrzyjmy się rysunkowi.

Zauważmy, że odległość punktu od boku jest równa długości odcinka , czyli jest połową wysokości poprowadzonej na ten bok. Podobnie, odległość punktu od boku jest równa długości odcinka , czyli jest połową wysokości poprowadzonej na ten bok. Pole można wyrazić jako iloczyn lub jako iloczyn , stąd . Zatem , stąd .
Ale , zatem . Stąd oraz .
Pozostaje nadmienić, że szukany równoległobok okazał się być prostokątem.
Trójkąty przystające w rombie
Romb jest oczywiście równoległobokiem, ale istnieje zasadniczy powód, dla którego warto ten czworokąt wyróżnić i omówić oddzielnie. Na początek udowodnimy własność, z której korzysta się bardzo często, nie wgłębiając się w jej uzasadnienie – przekątne rombu dzielą go na cztery trójkąty przystające.
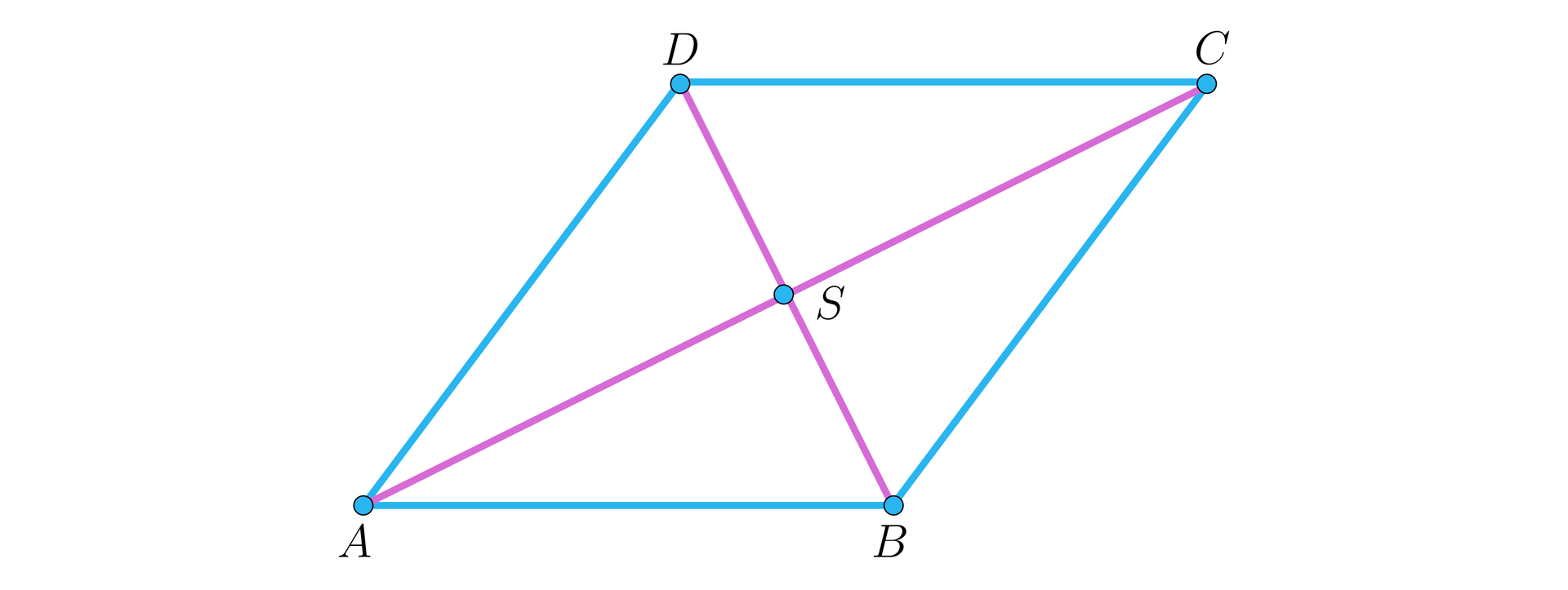
Zauważmy, na mocy cechy bok‑bok‑bok, że . Ale każdy z trójkątów i jest równoramienny, zatem . Wiemy, że w dowolnym równoległoboku przekątne się połowią, zatem oraz . Stąd, na mocy cechy bok‑kąt‑bok przystające są trójkąty i oraz i . Analogicznie, na mocy cechy bok‑kąt‑bok przystające są trójkąty i . Relacja przystawania jest przechodnia, co oznacza, że .
Oczywiście, kąty tych przystających trójkątów przy wierzchołku są równe, co oznacza, że każdy z nich jest kątem prostym. Tym samym wykazaliśmy nie tylko, że przekątne rombu dzielą go na cztery trójkąty przystające, ale, że każdy z tych trójkątów jest prostokątny.
Warto wspomnieć, że prostopadłość przekątnych równoległoboku jest warunkiem wystarczającym, by taki równoległobok był rombem.
Dłuższa przekątna rombu ma długość , a promień okręgu o środku , wpisanego w ten romb, jest równy . Wyznaczymy pole i długość boku rombu.
Przyjmijmy oznaczenia, jak na rysunku, gdzie jest punktem, w którym okrąg wpisany jest styczny do boku .

Wykazaliśmy wcześniej, że każdy z trójkątów, na które przekątne dzielą dowolny romb, jest trójkątem prostokątnym – w szczególności trójkąt . Zauważmy, że , zatem trójkąty i są podobne oraz . Ale . Zatem z warunku wynika, że . Stąd . Możemy już obliczyć pole rombu, jako sumę pól czterech trójkątów prostokątnych: .
Długość boku rombu można obliczyć korzystając np. z twierdzenia Pitagorasa, wtedy . Można też zauważyć, że wysokość rombu jest równa średnicy okręgu wpisanego i skorzystać z obliczonego wcześniej pola. Wtedy . Stąd oczywiście .
Słownik
zestaw twierdzeń określających warunki równoważne występowania relacji przystawania między dwoma trójkątami
odcinek łączący środki ramion w trapezie, jego długość jest średnią arytmetyczną długości podstaw
czworokąt, który ma co najmniej jedną parę boków równoległych