Przeczytaj

W sytuacjach, w których określamy odległości czy też długości, szerokości i wysokości obiektów w terenie, możemy posłużyć się metodami, którymi posługują się m.in. geodeci.

Przypomnijmy wartości funkcji trygonometrycznych dla kątów: $30 °$ , $45 °$ , $60 °$ :

$α$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$
$\sin α$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$
$\cos α$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$
$tg α$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$

Przykład 1

Samolot widać pod kątem $30 °$ w momencie, gdy znajduje się on nad punktem odległym od obserwatora o $2 km$ . Wyznaczymy, na jakiej wysokości i w jakiej odległości od obserwatora znajduje się ten samolot.

R2bFRxCevQzhc

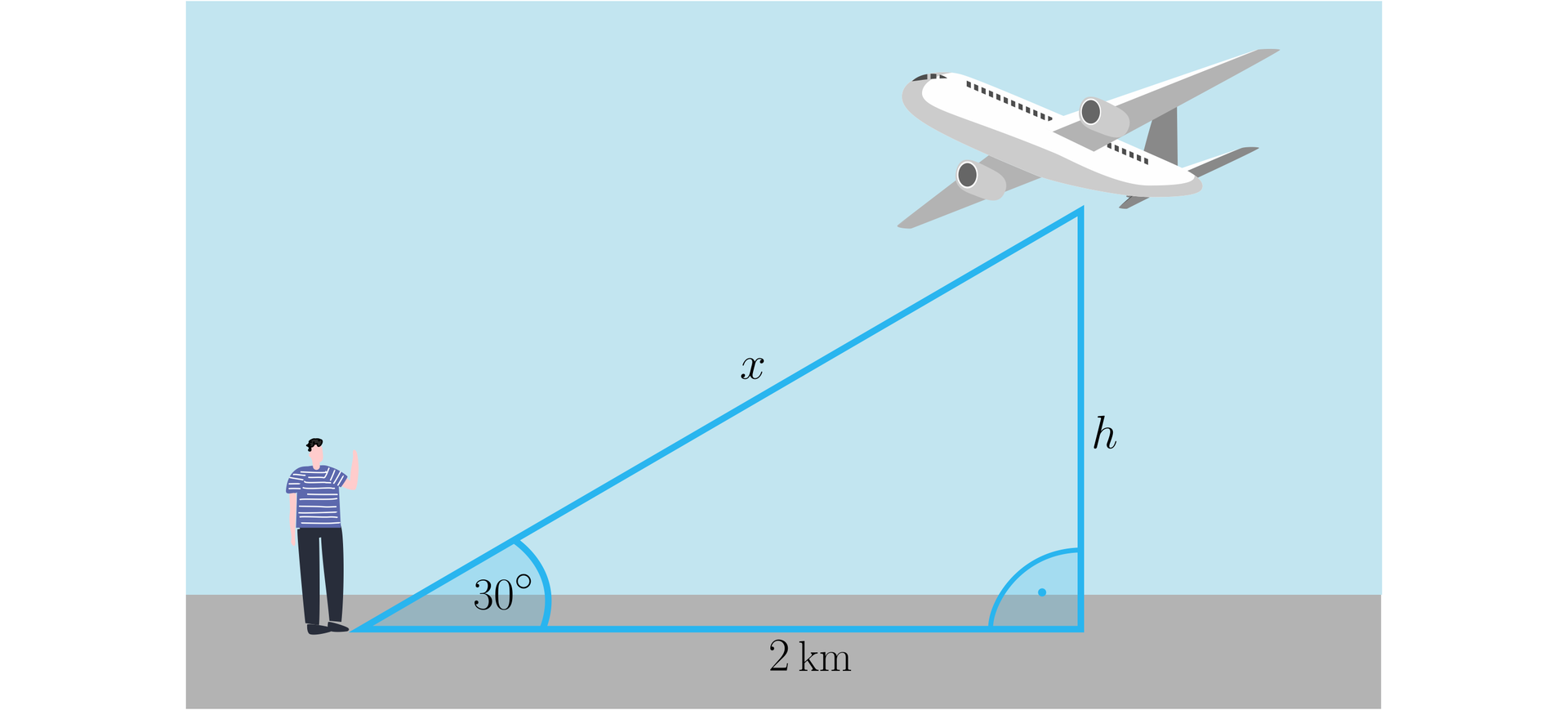
Ilustracja przedstawia człowieka stojącego na ziemi i lecący nad nim samolot. Na rysunek naniesiono trójkąt prostokątny, w którym pozioma przyprostokątna to odległość między człowiekiem a poziomym rzutem samolotu. Odległość ta wynosi 2 kilometry. Pionowa przyprostokątna h to wysokość na jakiej wznosi się samolot. Przeciwprostokątna z to odległość od stóp człowieka do środka samolotu. Między bokiem h a podstawą oznaczono kąt prosty, a między bokiem x a podstawą zaznaczono kąt o mierze 30 stopni.

Wprowadzamy oznaczenia:

$h$ – wysokość na jakiej znajduje się samolot,
$x$ – odległość samolotu od obserwatora.

Skonstruowany trójkąt jest prostokątny - wyznaczając wysokość, na jakiej znajduje się samolot, wykorzystamy funkcję tangens.

$tg 30 ° = \frac{h}{2}$ , a ponieważ

$tg 30 ° = \frac{\sqrt{3}}{3}$ , to po następujących przekształceniach

$\frac{\sqrt{3}}{3} = \frac{h}{2}$

$3 \cdot h = \sqrt{3} \cdot 2$

otrzymujemy

$h = \frac{2 \sqrt{3}}{3} \approx 1, 15 km$ .

Obliczamy wysokość, na jakiej znajduje się samolot, wykorzystując funkcję sinussinus kąta ostrego $α$ sinus:

$\sin 30 ° = \frac{h}{x}$ , a ponieważ

$\sin 30 ° = \frac{1}{2}$ , to

$\frac{1}{2} = \frac{h}{x}$ , stąd

$x = 2 h$

Ostatecznie otrzymujemy

$x = \frac{2 \cdot 2 \sqrt{3}}{3} = \frac{4 \sqrt{3}}{3} \approx 2, 30$ .

Odpowiedź: Samolot znajduje się na wysokości około $1, 15 km$ , w odległości około $2, 30 km$ od obserwatora.

Przykład 2

Z wieży o wysokości $h = 42 m$ zmierzono kąty depresjikąt depresjikąty depresji obu brzegów rzeki otrzymując $α = 60 °$ i $β = 30 °$ . Obliczymy szerokość rzeki i odległość wieży od rzeki.

R15DPrBQDIzFu

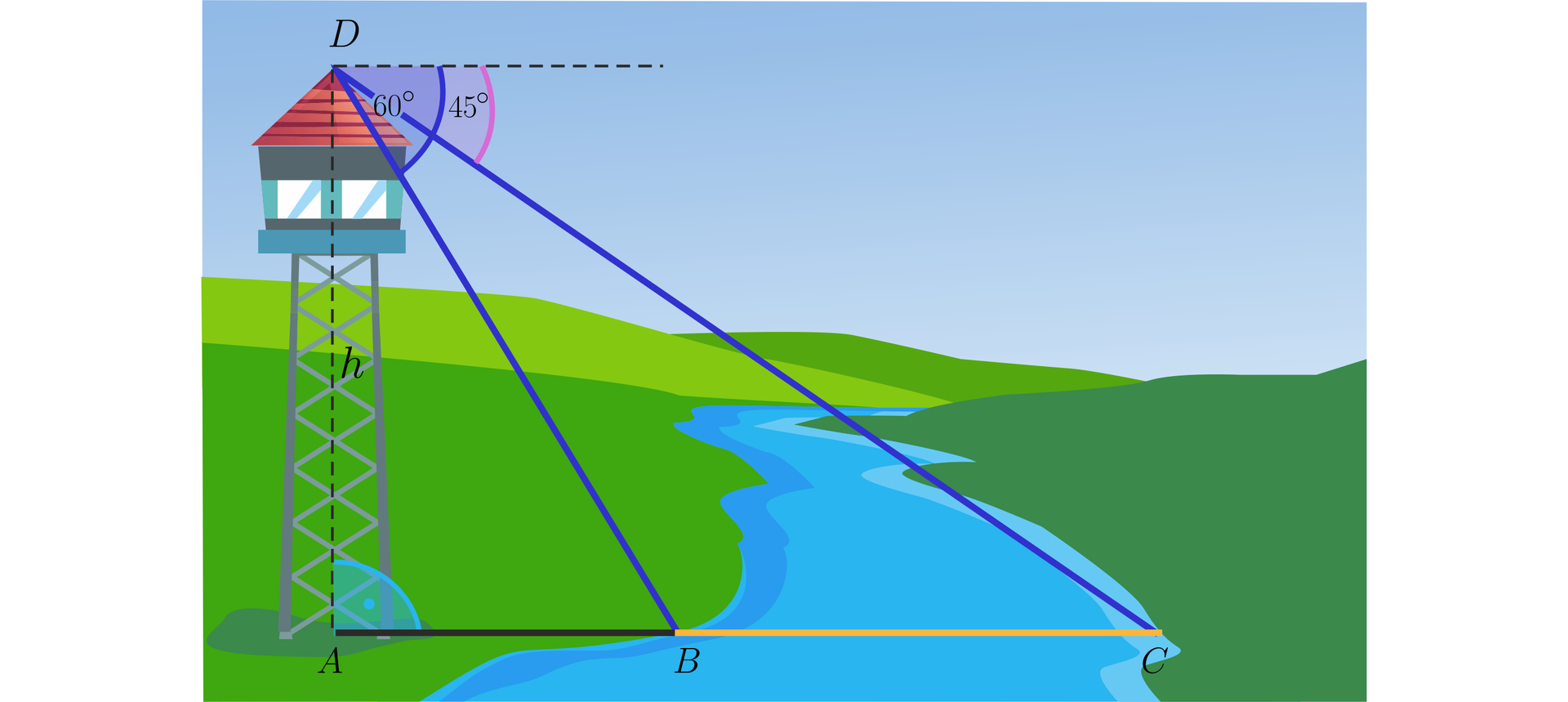
Ilustracja przedstawia wieżę o wysokości h stojącą nad rzeką. Wieża znajduje się w lewej części rysunku, a rzeka w prawej. Na rysunek naniesiono cztery punkty. Punkt A znajduje się w podstawie wieży, punkt D zaś na jej szczycie. Z punktu A poprowadzono dwa pokrywające się poziome odcinki. Pierwszy do punktu B, który znajduje się na lewym brzegu rzeki. Drugi do punktu C znajdującym się na prawym brzegu rzeki. Ze szczytu wieży poprowadzono linią przerywaną poziomą linię, w oparciu o którą oznaczono dwa kąty: kąt o mierze 45 stopni między linią przerywaną a odcinkiem C D oraz kąt o mierze 60 stopni między linią przerywaną a odcinkiem B D.

Powstały tu dwa trójkąty prostokątne: $Δ D A B$ i $Δ D A C$ .

RnjVyk0t4IDrD

Ilustracja przedstawia dwa trójkąty prostokątne. Z lewej mamy trójkąt A B D, gdzie pionowy bok A D oznaczono literą h, a poziomą przyprostokątną A B oznaczono jako x. Z górnego wierzchołka D poprowadzono linią przerywaną poziomy odcinek i między linią a bokiem B D trójkąta zaznaczono kąt o mierze 60 stopni. Kąt ten dał nam informację o kątach wewnętrznych trójkąta, ponieważ kąt przy wierzchołku D to 90 stopni odjąć 60 stopni, czyli 30 stopni. Przy wierzchołku A znajduje się kąt prosty, a więc przy wierzchołku B znajduje się kąt 60 stopni. Z prawej mamy trójkąt A C D, gdzie pionowy bok A D oznaczono literą h, a poziomą przyprostokątną A B oznaczono jako y. Z górnego wierzchołka D poprowadzono linią przerywaną poziomy odcinek i między linią a bokiem C D trójkąta zaznaczono kąt o mierze 45 stopni. Kąt ten dał nam informację o kątach wewnętrznych trójkąta, ponieważ kąt przy wierzchołku D to 90 stopni odjąć 45 stopni, czyli 45 stopni. Przy wierzchołku A znajduje się kąt prosty, a więc przy wierzchołku C znajduje się kąt 45 stopni.

$h = 42$

Wprowadzamy oznaczenia:

$h$ – wysokość wieży,
$x$ – odległość wieży od rzeki,
$|A B| = x$ ,
$|A C| = y$ .

Trójkąt $D A B$ jest prostokątny. Możemy zatem obliczyć odległość $x$ , czyli odległość wieży od rzeki, korzystając z funkcji tangenstangens kąta ostrego $α$ tangens.

$tg 60 ° = \frac{|A D|}{|A B|} = \frac{h}{x}$

Podstawiając $h = 42 m$ oraz $tg 60 ° = \sqrt{3}$ , otrzymujemy

$\sqrt{3} = \frac{42}{x}$ , czyli

$x = \frac{42}{\sqrt{3}} \approx 24 m$ .

Trójkąt $A C D$ jest prostokątny i równoramienny, stąd $|A C| = |A D|$ , więc $y = h$ .

Zatem mamy, że $y \approx 42 m$ .

Szerokość rzeki jest różnicą długości odcinków $A C$ i $A B$ .

$|A C| - |A B| = y - x \approx 42 m - 24 m = 18 m$

Odpowiedź: Szerokość rzeki wynosi około $18 m$ , a wieża oddalona jest oddalona od rzeki o około $24 m$ .

Przykład 3

Obliczymy, ile metrów siatki należy kupić, aby ogrodzić działkę mającą kształt prostokąta, którego przekątna ma długość $100 m$ , a jeden z kątów między przekątnymi ma miarę $60 °$ . Wynik podamy z dokładnością do $1 m$ .

RiqDAhxIC6QWB

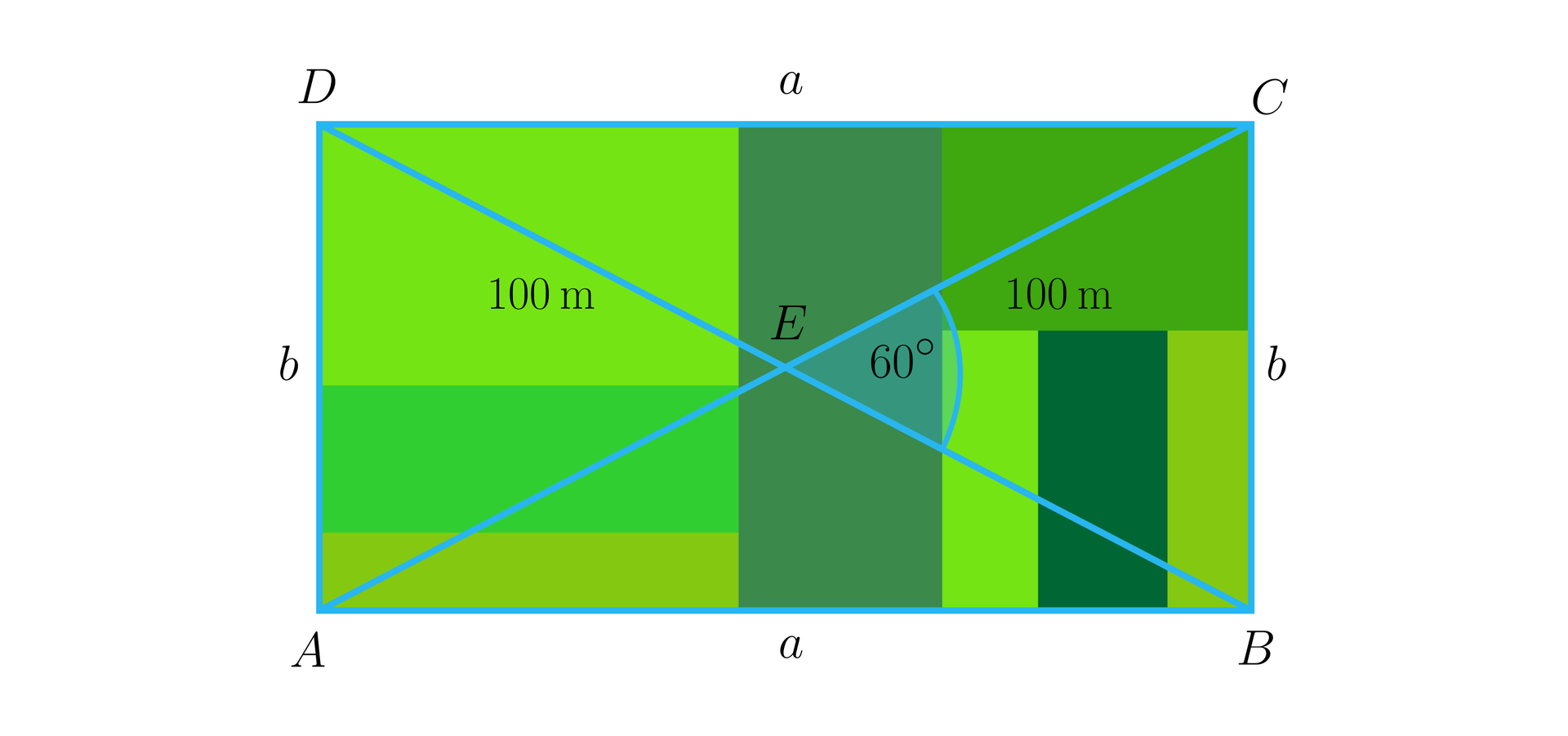
Ilustracja przedstawia prostokąt A B C D, gdzie poziome boki A B i C D oznaczono literą a, natomiast pionowe boki A D oraz B C oznaczono literą b. W prostokącie wykreślono przekątne o długości 100 metrów każda. Przecinają się one w punkcie E pod kątem 60 stopni.

W prostokącie przeciwległe boki są równe: $|A B| = |D C| = a$ i $|B C| = |A D| = b$ oraz przekątne są tej samej długości: $d = |A C| = |D B| = 100 m$ i przecinają się w połowie.

Przekątne przecinają się w połowie, więc przy oznaczeniach jak na rysunku zapisujemy: $|A E| = |C E| = |D E| = |B E| = 50 m$ .

Ponieważ trójkąt $B E C$ jest równoboczny ( $|B E| = |C E|$ i kąt $C E B$ ma miarę $60 °$ ), to $b = |B E| = |C E| = |B C|$ , czyli $b = 50 m$ .

Mamy zatem długość boku: $b = 50 m$ .

Rozważmy teraz trójkąt prostokątny $E F B$ , gdzie $E F$ jest wysokością trójkąta $A B E$ .

REJeS1gcSVMHO

Ilustracja przedstawia prostokąt A B C D, gdzie pionowe boki A D oraz B C mają długość 50 metrów. W prostokącie wykreślono przekątne przecinające się w punkcie E pod kątem 60 stopni. Z punktu E upuszczono pionowy odcinek na dolny bok A B figury. Jest to odcinek E F. Między odcinkiem a bokiem A B oznaczono kąt prosty. Oznaczono również kat F B E o mierze 30 stopni oraz kąt E B C o mierze 60 stopni.

Trójkąt $E F B$ jest prostokątny. Korzystając z funkcji cosinuscosinus kąta ostrego $α$ cosinus, obliczymy $a$ .

$\cos 30 ° = \frac{|F B|}{|B E|}$

Podstawiając $|A F| = |F B| = \frac{1}{2} a$ oraz $|B E| = b = 50 m$ , otrzymujemy

$\cos 30 ° = \frac{\frac{1}{2} a}{50}$ .

A ponieważ $\cos 30 ° = \frac{\sqrt{3}}{2}$ , to zapisujemy:

$\frac{\sqrt{3}}{2} = \frac{a}{100}$ .

Ostatecznie mamy:

$a = \frac{100 \sqrt{3}}{2} = 50 \sqrt{3} m$ .

Zatem długość drugiego boku wynosi $a = 50 \sqrt{3} m$ .

Obliczmy obwód $L$ tego prostokąta.

$L = 2 a + 2 b$

$L = 2 \cdot 50 \sqrt{3} + 2 \cdot 50 = 100 \sqrt{3} + 100 \approx 273, 2 m$

Odpowiedź: Należy zakupić $274 m$ siatki (gdybyśmy zakupili $273 m$ zabrakłoby nam materiału i nie ogrodzilibyśmy całej działki).

Przykład 4

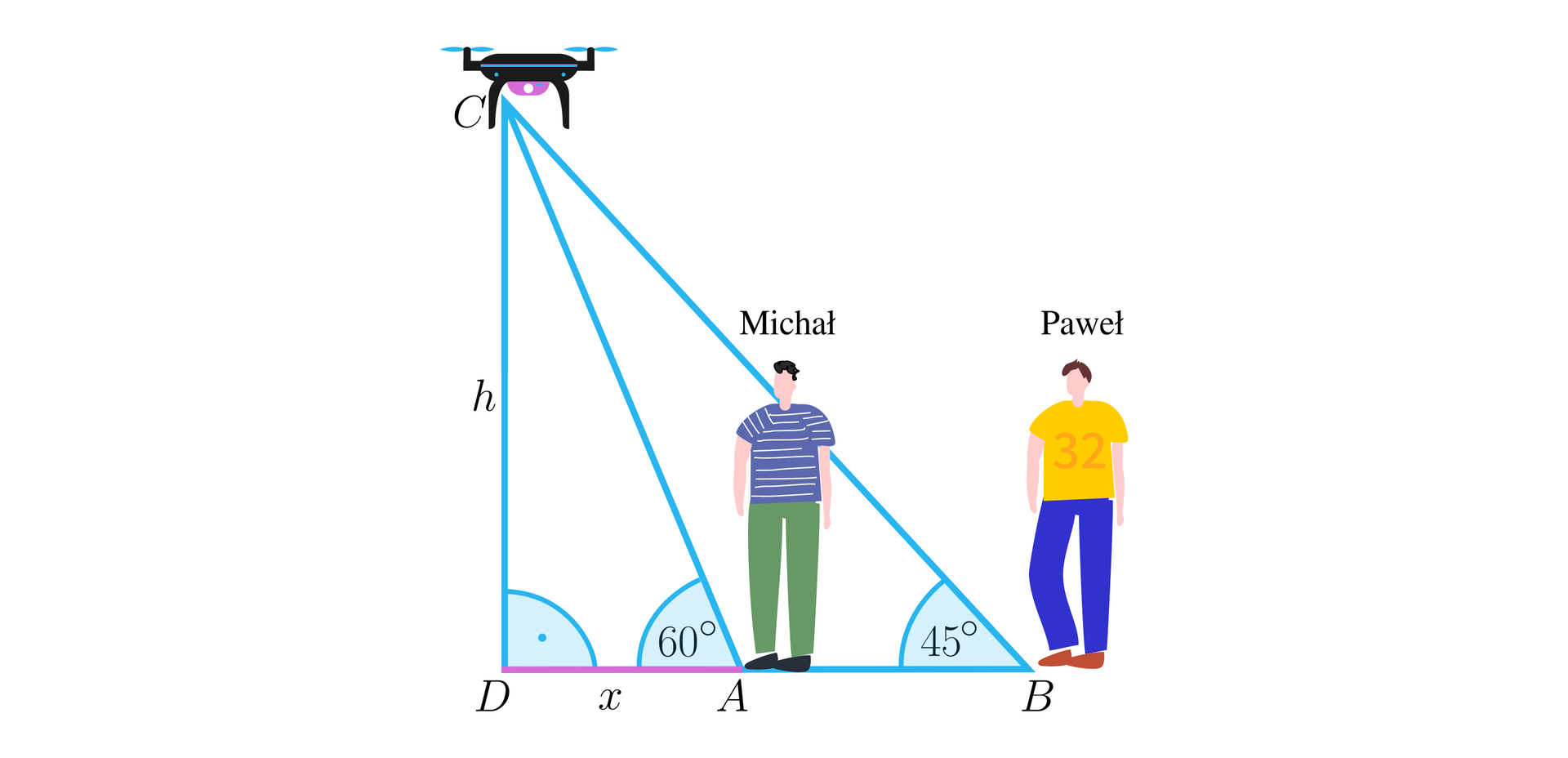
Michał i Paweł, obaj tego samego wzrostu, stojąc w odległości $100 m$ od siebie, obserwują latającego nad nimi drona. W tym samy momencie Michał widzi go pod kątem $60 °$ , a Paweł pod kątem $45 °$ . Obliczymy, na jakiej wysokości znajdował się dron.

Musimy rozpatrzyć dwie sytuacje.

$1)$ Przyjmijmy oznaczenia jak na rysunku.

RpygR7Cuqp2d6

Ilustracja przedstawia stojącego z lewej strony Michała (oznaczonego punktem A) i stojącego z prawej strony Pawła (oznaczonego punktem B). Nad chłopcami wznosi się dron (oznaczony punktem C). Na rysunek naniesiono trójkąt A B C, gdzie pozioma podstawa A B wyznacza odległość między chłopcami. Lewy bok A C to odległość między Michałem a dronem, a prawy bok B C to odległość między Pawłem a dronem. Z punktu C upuszczono wysokość h, która biegnie do punktu D. Odcinek A D wyróżniono kolorem i oznaczono literą x. Odcinek D B opisano jako 100 odjąć x. Bok A C nachylony jest do podstawy pod kątem 60 stopni, a bok B C nachylony jest do podstawy pod kątem 45 stopni.

Wprowadźmy oznaczenia:

$|A B| = 100 m$ (odległość między chłopcami),

$|D C| = h$ (wysokość na jakiej wznosi się dron),

$|A D| = x$ ,

$|A D| + |D B| = 100$ , więc

$|D B| = 100 - x$ .

Trójkąt $C D B$ jest równoramienny, ponieważ jest to trójkąt prostokątny z kątem o mierze $45 °$ przy podstawie.

$|D B| = |D C| = h = 100 - x$ , stąd

$h = 100 - x$ .

Dla trójkąta prostokątnego $A D C$ mamy zależność: $tg 60 ° = \frac{h}{x}$ .

Wiemy również, że $tg 60 ° = \sqrt{3} \approx 1, 73$ .

Podstawiając: $x = 100 - h$ (bo $h = 100 - x$ ), otrzymujemy:

$\sqrt{3} = \frac{h}{100 - h}$

$\sqrt{3} (100 - h) = h$ .

Ponieważ $\sqrt{3} \approx 1, 73$ , to po przekształceniach otrzymamy

$h \approx 63 m$ .

Odpowiedź: Dron znajduje się na wysokości około $63 m$ .

$2)$ Michał stoi odwrócony plecami do Pawła.

Rppj5hvHGkm5J

Ilustracja przedstawia wznoszącego się z lewej strony drona (oznaczonego punktem C). Pośrodku rysunku znajduje się Michał (oznaczony punktem A), a po prawej stronie Paweł (oznaczony punktem B). Od drona poprowadzono w dół pionowy odcinek h do punktu D znajdującego się na ziemi. Na rysunek naniesiono dwa trójkąty prostokątne. Trójkąt D A C, gdzie pionowa przyprostokątna to odcinek C D oznaczony jako h, pozioma przyprostokątna to odcinek D A oznaczony jako x, a przeciwprostokątna A C jest nachylona pod kątem 60 stopni do podstawy. Drugi trójkąt to D B C, gdzie pionowa przyprostokątna to odcinek C D oznaczony jako h, pozioma przyprostokątna to odcinek D B, a przeciwprostokątna B C jest nachylona pod kątem 45 stopni do podstawy.

$|A B| = 100 m$ (odległość między chłopcami)

$h = |D C|$ (wysokość na jakiej wznosi się dron)

$x = |D A|$

Powstały trójkąt $C D B$ jest prostokątny i równoramienny, ponieważ jest to trójkąt prostokątny z kątem o mierze $45 °$ przy podstawie.

$h = |D C| = |D B| = x + 100$

$h = x + 100$ , stąd

$x = h - 100$ .

Z trójkąta prostokątnego $C D A$ mamy:

$tg 60 ° = \frac{h}{x}$ .

Podstawiając: $x = h - 100$ oraz $tg 60 ° = \sqrt{3}$ , otrzymujemy:

$\sqrt{3} = \frac{h}{h - 100}$ .

Ponieważ $\sqrt{3} \approx 1, 73$ , to po przekształceniach otrzymujemy:

$h \approx 237 m$ .

Odpowiedź: Dron znajduje się na wysokości około $237 m$ .

Słownik

sinus kąta ostrego

α

sinus kąta ostrego

α

sinusem kąta ostrego $α$ w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej kątowi $α$ do długości przeciwprostokątnej

cosinus kąta ostrego

α

cosinus kąta ostrego

α

cosinusem kąta ostrego $α$ w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do kąta $α$ do długości przeciwprostokątnej

tangens kąta ostrego

α

tangens kąta ostrego

α

tangensem kąta ostrego $α$ w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej kątowi $α$ do długości przyprostokątnej przyległej do kąta $α$

kąt depresji

kąt płaski pomiędzy płaszczyzną poziomą przechodzącą przez oko obserwatora (zwaną płaszczyzną horyzontu) a prostą łączącą oko z punktem znajdującym się pod tą płaszczyzną; jeżeli punkt znajduje się nad tą płaszczyzną, to kąt nazywa się kątem wznoszenia lub elewacją

Wprowadzenie

Animacja

Słownik