Przeczytaj

Pamiętasz?

Nierównością kwadratową z niewiadomą $x$ nazywamy każdą nierówność postaci

$a x^{2} + b x + c > 0$ lub $a x^{2} + b x + c \geq 0$ lub $a x^{2} + b x + c < 0$ lub $a x^{2} + b x + c \leq 0,$

gdzie:
$a$ , $b$ , $c$ – są ustalonymi liczbami rzeczywistymi i $a \neq 0$ .

Nierówności, w których wszystkie współczynniki są różne od $0$ , nazywamy nierównościami kwadratowymi zupełnymi.

Nierówności, w których współczynniki $b$ lub $c$ są równe $0$ , nazywamy nierównościami kwadratowymi niezupełnyminierówność kwadratowa niezupełnanierównościami kwadratowymi niezupełnymi.

Jeżeli $b = 0$ i $c = 0$ to nierówność kwadratowa jest postaci $a x^{2} > 0$ lub $a x^{2} < 0$ lub $a x^{2} \geq 0$ lub $a x^{2} \leq 0$ .

Przykład 1

Obliczymy dla jakich wartości parametru $m$ zbiorem rozwiązań nierówności $2 x^{2} + m^{2} - 3 > 0$ jest zbiór liczb rzeczywistych.

Rozwiązanie

Aby zbiorem rozwiązań nierówności $2 x^{2} + m^{2} - 3 > 0$ był $ℝ$ - zbiór liczb rzeczywistych - wykres funkcji $f (x) = 2 x^{2} + m^{2} - 3$ musi w układzie współrzędnych znajdować się powyżej osi $X$ .

Czyli $m^{2} - 3 > 0$

$(m - \sqrt{3}) (m + \sqrt{3}) > 0$

$m \in (- \infty, - \sqrt{3}) \cup (\sqrt{3}, \infty)$ .

Przykład 2

Znajdziemy wszystkie rzeczywiste wartości parametru $m$ dla których zbiorem rozwiązań poniższej nierówności kwadratowej niezupełnej z niewiadomą $x$ jest zbiór $(0, 1)$ .

$- x^{2} + (2 m - 3) x > 0$

Rozwiązanie

Obliczymy miejsca zerowe funkcji $f (x) = - x^{2} + (2 m - 3) x$ .

$- x^{2} + (2 m - 3) x = 0$

$x [- x + (2 m - 3)] = 0$

$x = 0$ lub $x = 2 m - 3$

Szkicujemy parabolę przechodzącą przez wyznaczone punkty. Ramiona paraboli skierowane są do dołu, bo współczynnik przy $x^{2}$ jest ujemny. Pierwiastek $x = 2 m - 3 > 0$ .

R8NPHobqV2wtP

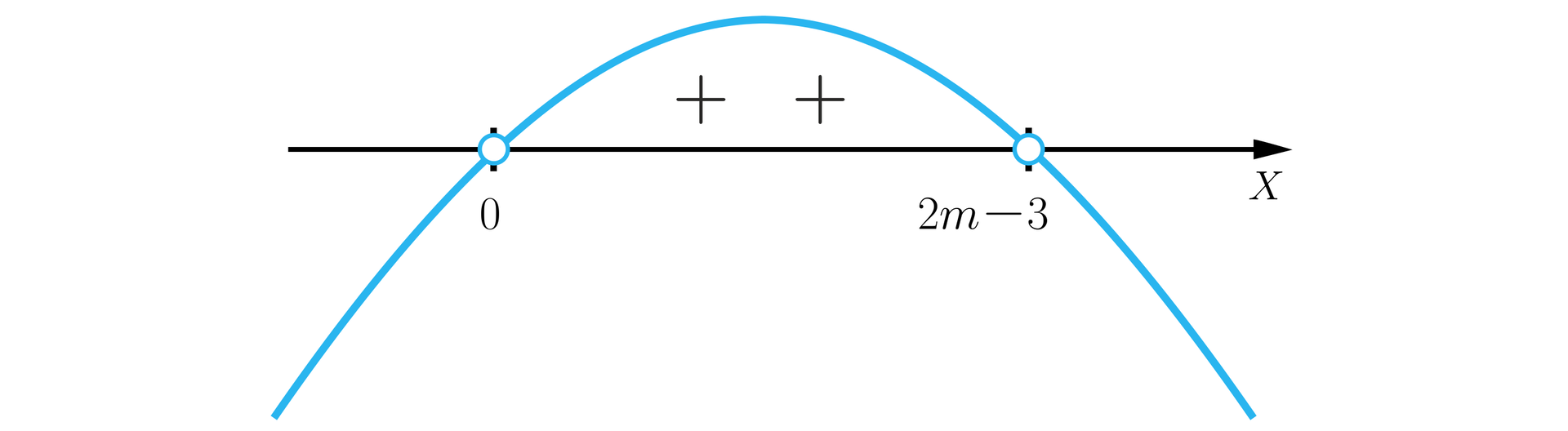
Rysunek przedstawia poziomą oś X z zaznaczonymi na niej liczbami: 0 oraz liczba większa od zera zapisana w postaci 2 m odjąć 3. Liczby zaznaczono niezamalowanymi kółkami i poprowadzono przez nie wykres wielomianu tak, że od minus nieskończoności do zera wykres znajduje się pod osią, w zerze przechodzi nad oś i wraca pod oś w punkcie 2 odjąć 3. Fragment nad osią oznaczono plusami znajdującymi się między osią a wykresem.

Zatem $2 m - 3 = 1$

$2 m = 4$

$m = 2$

Aby zbiorem rozwiązań nierówności był zbiór $(0, 1)$ , parametr $m = 2$ .

Przykład 3

Dla jakich wartości parametru $m$ funkcja $f (x) = \sqrt{(2 m - 1) x^{2} + 1}$ jest określona dla każdej liczby $x \in ℝ$ ?

Rozwiązanie

Wyrażenie znajdujące się pod pierwiastkiem musi być nieujemne, zatem musi być spełniony warunek $(2 m - 1) x^{2} + 1 \geq 0$ .

Czyli $2 m - 1 \geq 0$

$2 m \geq 1$

$m \geq \frac{1}{2}$

$m \in ⟨\frac{1}{2}, \infty)$

Aby funkcja $f$ była określona dla $x \in ℝ$ , $m \in ⟨\frac{1}{2}, \infty)$ .

Przykład 4

Wyznaczymy takie wartości parametru $k$ , dla których liczba $2$ zawiera się w zbiorze rozwiązań nierówności $- x^{2} + 4 k x > 0$ .

Rozwiązanie

$- x^{2} + 4 k x > 0$

$x (- x + 4 k) > 0$

Obliczymy miejsca zerowe funkcji $f (x) = x (- x + 4 k)$ .

$x (- x + 4 k) = 0$

$x = 0$ lub $x = 4 k$

Ponieważ liczba $2$ należy do zbioru rozwiązań nierówności, więc $4 k$ jest większym pierwiastkiem.

RMulBW5GqDDfL

Rysunek przedstawia poziomą oś X z zaznaczonymi na niej liczbami: 0, 2 oraz liczba większa od dwóch zapisana w postaci 4 k. Liczby 0 i 4 k zaznaczono niezamalowanymi kółkami i poprowadzono przez nie wykres wielomianu tak, że od minus nieskończoności do zera wykres znajduje się pod osią, w zerze przechodzi nad oś i wraca pod oś w punkcie 4 k. Fragment nad osią oznaczono plusami znajdującymi się między osią a wykresem.

Czyli $4 k > 2$ .

$k > \frac{1}{2}$

Aby liczba $2$ zawierała się w zbiorze rozwiązań nierówności dla $k \in (\frac{1}{2}, \infty)$ .

Przykład 5

Obliczymy, dla jakich wartości parametru $p$ nierówność $p x^{2} + 2 p + 4 > 0$ nie ma rozwiązań.

Rozwiązanie

Aby nierówność kwadratowa $p x^{2} + 2 p + 4 > 0$ nie posiadała rozwiązań muszą być spełnione warunki:

$\{\begin{cases} 1 . p < 0 \\ 2 . 2 p + 4 < 0 \end{cases}$

$p \in (- \infty, 0)$

$2 p + 4 < 0$
$2 p < - 4$
$p < - 2$
$p \in (- \infty, - 2)$

Uwzględniając koniunkcję warunków $(1)$ i $(2)$ otrzymujemy, że $p \in (- \infty, - 2)$ .

Jeżeli współczynnik przy $x^{2}$ będzie równy zero:

$p = 0$

$4 \geq 0$

Otrzymaliśmy nierówność prawdziwą dla dowolnego $x \in ℝ$ . Czyli liczba $0$ nie spełnia warunków zadania.

Nierówność nie posiada rozwiązań dla $p \in (- \infty, - 2)$ .

Słownik

nierówność kwadratowa niezupełna

nierówność, w której współczynnik $b$ lub $c$ jest równy zero

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik