Przeczytaj

Czworokąt wpisany w okrąg i trójkąty

Zauważmy na poniższym rysunku, że okrąg opisany na czworokącie $A B C D$ jest tym samym okręgiem, który jest opisany na każdym z trójkątów $A C D$ i $A B C$ .

R1MXefXwNeOoL

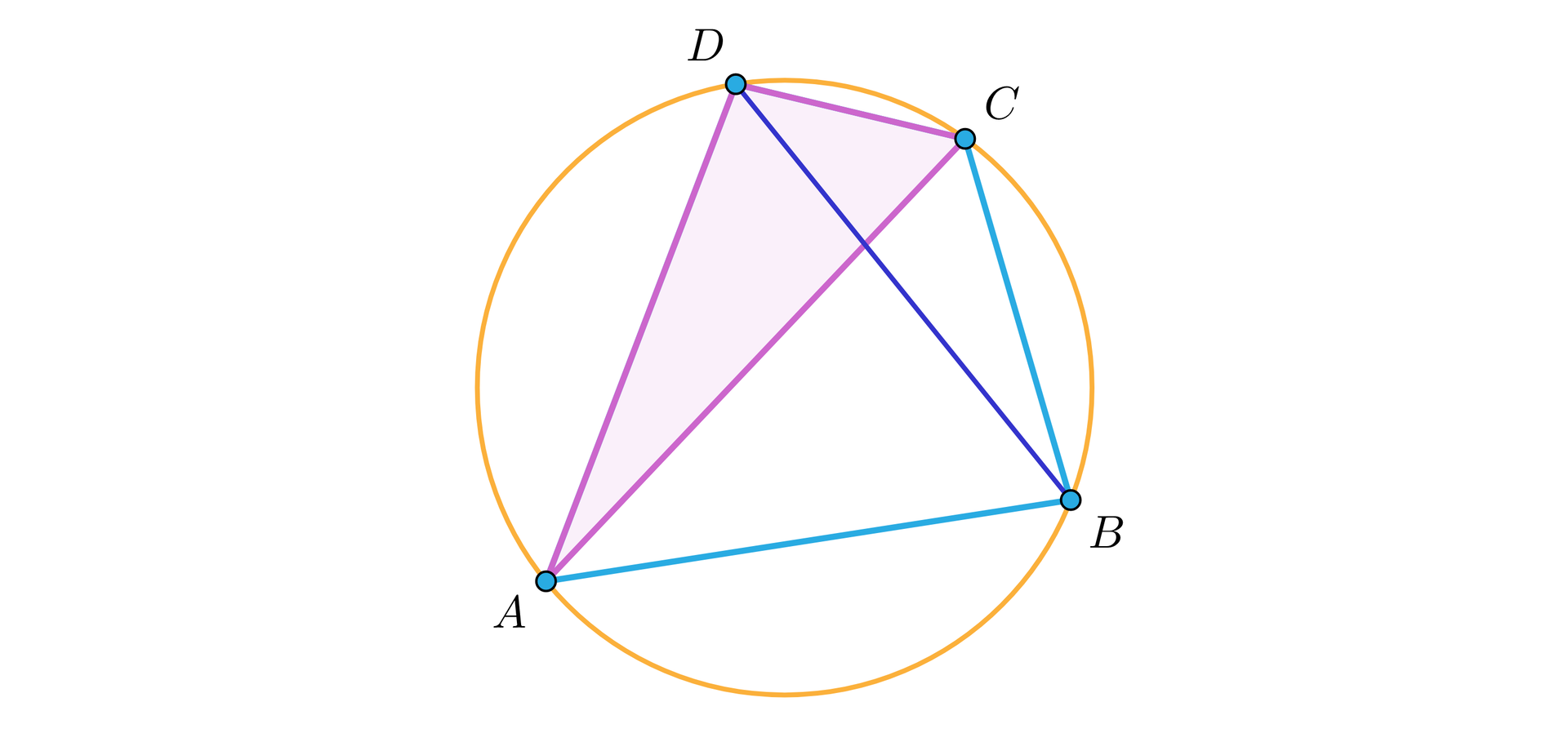
Ilustracja przedstawia czworokąt nieforemny A B C D wpisany w okrąg. Zaznaczono przekątne czworokąta AC i BD. Kolorem wyróżniono trójkąt A C D będący częścią czworokąta. — Czworokąt i trójkąty wpisane w okrąg

Zauważmy jednak, że obraz trójkąta $A C D$ w symetrii w względem symetralnej odcinka $A C$ także jest wpisany w ten sam okrąg, jak na rysunku.

RzH4GjpwHme7x

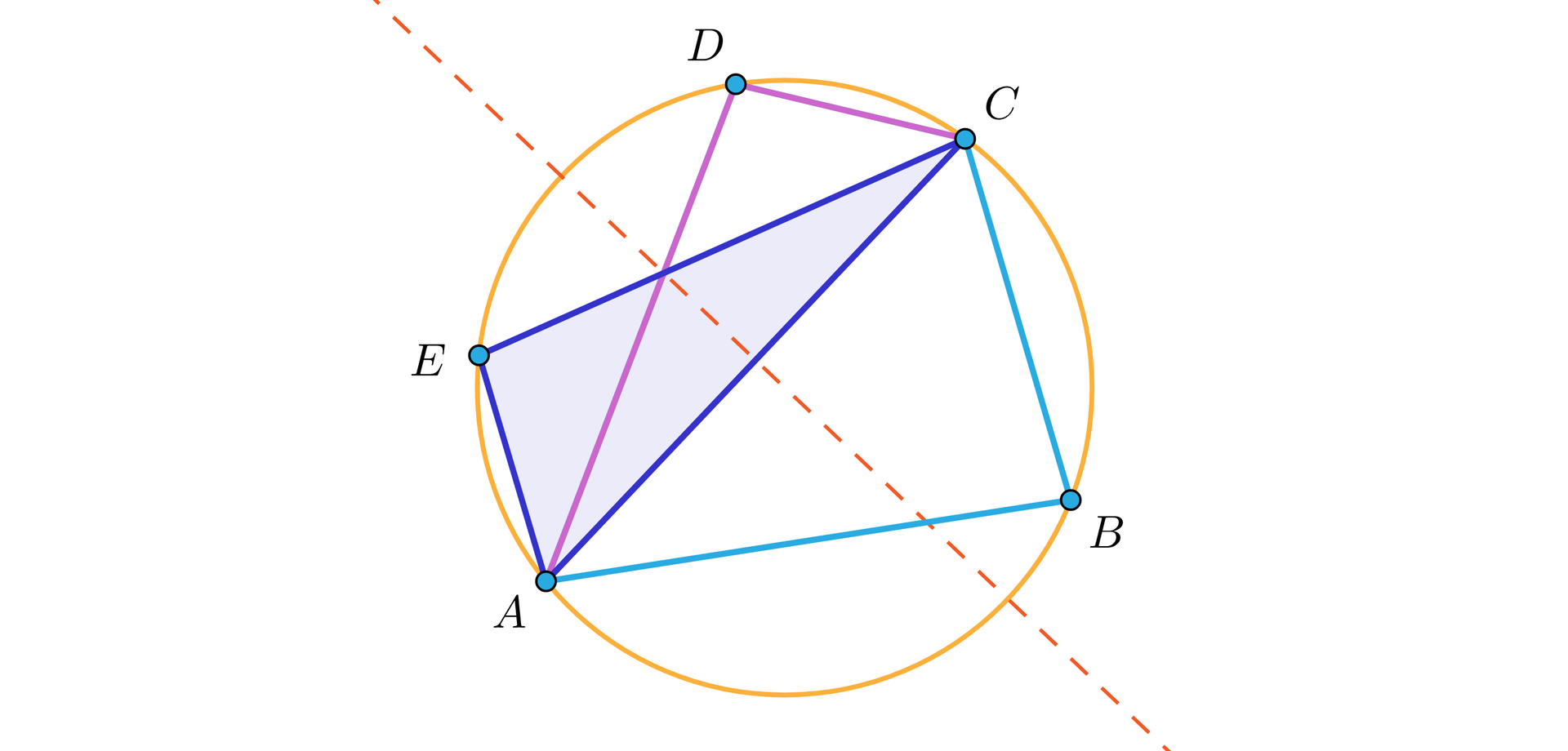
Ilustracja przedstawia czworokąt A B C D wpisany w okrąg. Dorysowano punkt E na okręgu i kolorem wyróżniono trójkąt A C E oparty na przekątnej A C czworokąta. Linią przerywaną poprowadzono oś symetrii okręgu, która przebiega przez punkt przecięcia boków A D oraz E C. — Czworokąt i trójkąty symetryczne wpisane w okrąg

Tym samym otrzymujemy czworokąt cykliczny $A B C E$ , którego boki mają te same długości, co wyjściowa figura, ale ich porządek jest inny. Inna jest (może być) dla tych czworokątów miara kątów w wierzchołkach wyznaczonych przez końce przekątnej $A C$ . Analogicznie, można przekształcić odpowiednie trójkąty, gdy osią symetrii będzie symetralna odcinka $B D$ .

Powyższy fakt wykorzystamy dla dowodu poniższego twierdzenia.

Twierdzenie o przekątnej czworokąta cyklicznego

Twierdzenie: Twierdzenie o przekątnej czworokąta cyklicznego

Niech dany będzie czworokąt cykliczny o bokach długości $a$ , $b$ , $c$ , $d$ oraz przekątnych $p$ , $q$ , jak na rysunku.

RuJIiJMVU0ZOh

Ilustracja przedstawia czworokąt o bokach a b c d wpisany w okrąg. Jego przekątne mają długości q i p. — Twierdzenie o przekątnej czworokąta cyklicznego

Wtedy $p = \sqrt{\frac{(a c + b d) (a b + c d)}{a d + b c}}$ .

Dowód

Punktem wyjścia będzie dla nas twierdzenie Ptolemeusza, które orzeka, że w czworokącie cyklicznym iloczyn długości przekątnych jest równy sumie iloczynów długości odpowiednich boków, co przy powyższych oznaczeniach można zapisać, jako: $p \cdot q = a c + b d$ .

Zauważmy, że wspomniana wyżej symetria osiowa prowadzi do otrzymania jeszcze dwóch czworokątów cyklicznychwielokąt cyklicznycyklicznych o bokach tej samej długości, istotnie różnych, w szczególności o różnych przekątnych, jak na rysunku.

RD1UCBagWMAFq

Ilustracja przedstawia dwa okręgi, przy czym w każdy z nich wpisano czworokąt o bokach tej samej długość, przy czym w innej konfiguracji. W lewy okrąg wpisano czworokąt o bokach kolejno d b c a, w okrąg po prawej stronie wpisano czworokąt o bokach kolejno b d c s a. Oba czworokąty mają przekątne p i t.

Twierdzenie Ptolemeusza, zapisane dla każdego z tych czworokątów, pozwala zapisać odpowiednio równości:

$p \cdot t = a b + c d$ oraz $q \cdot t = a d + b c$ .

Wyznaczając z pierwszej równości zmienną $t = \frac{a b + c d}{p}$ i wstawiając ją do drugiego z równań otrzymujemy: $q \cdot \frac{a b + c d}{p} = a d + b c$ .

Stąd $q = \frac{a d + b c}{a b + c d} \cdot p$ .

Zatem $p \cdot \frac{a d + b c}{a b + c d} \cdot p = a c + b d$ , czyli $p^{2} = \frac{(a c + b d) (a b + c d)}{a d + b c}$ . Stąd wynika teza twierdzenia.

Analogicznie można wykazać, że $q = \sqrt{\frac{(a c + b d) (a d + b c)}{a b + c d}}$ .

Warto podkreślić, że mówiąc o symetrii odpowiednich trójkątów, na jakie przekątne podzieliły dany czworokąt, nie od razu widać równość długości przekątnej $t$ , jaka pojawia się w dowodzie, na pomocniczych rysunkach. Dlatego, zamiast o symetrii, wygodniej byłoby mówić o rozcinaniu czworokąta na trójkąty, których bokami są odpowiedni bok czworokąta oraz promienie poprowadzone do wierzchołków, jak na rysunku.

R8beGl7knyh8D

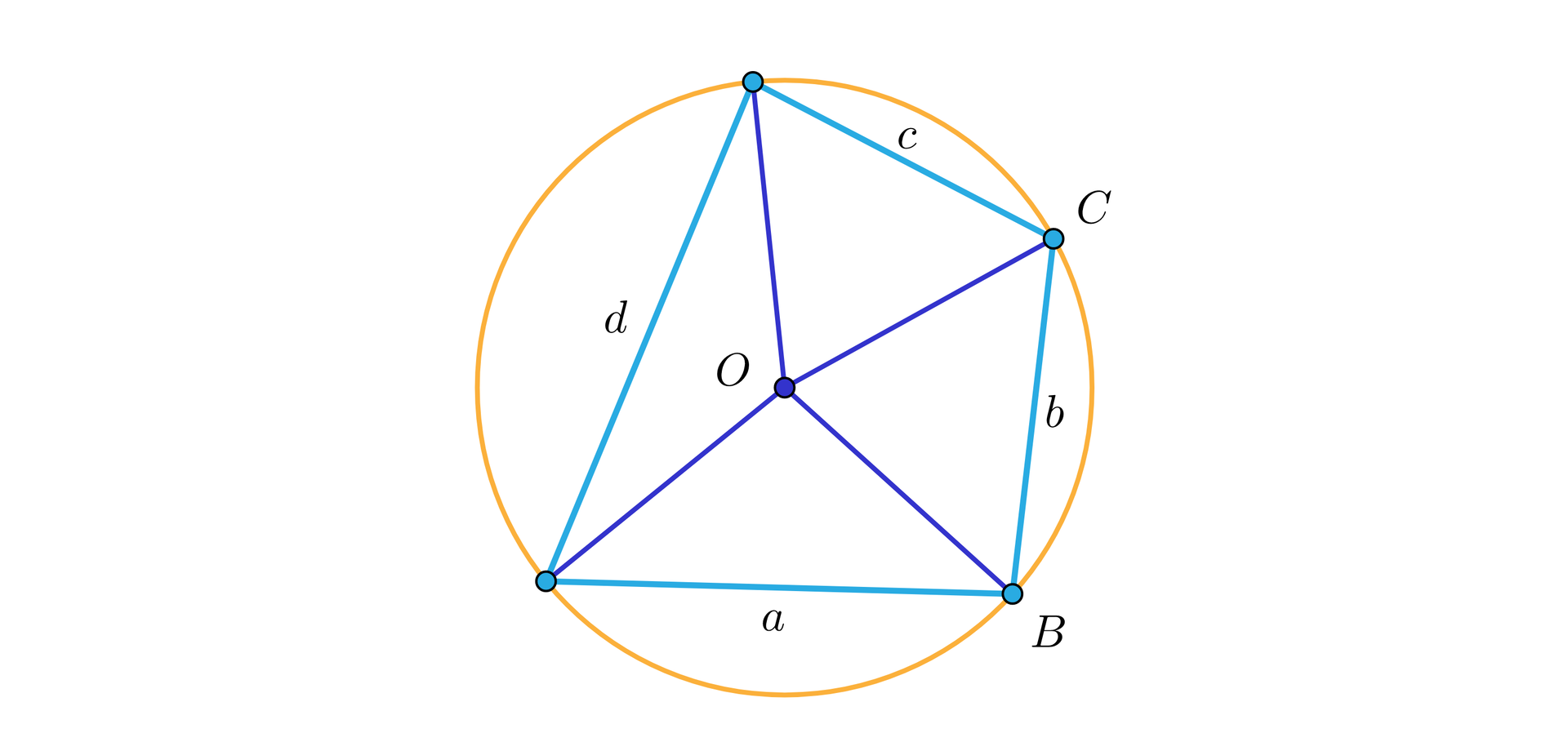
Ilustracja przedstawia czworokąt o bokach a b c d wpisany w okrąg. Zaznaczono środek okręgu i połączono wierzchołki czworokąta ze środkiem. — Rozcinanie czworokąta

Zmieniając kolejność ułożenia poszczególnych trójkątów otrzymamy różne czworokąty o takich samych bokach, wpisane w dany okrąg. Analizując w szczególności odpowiednie kąty łatwo dostrzec przystawanie odpowiednich figur.

Przejdźmy teraz do udowodnienia wzoru Brahmagupty. Przyjmijmy oznaczenia jak na rysunku.

R1ViAzPGuSDMO

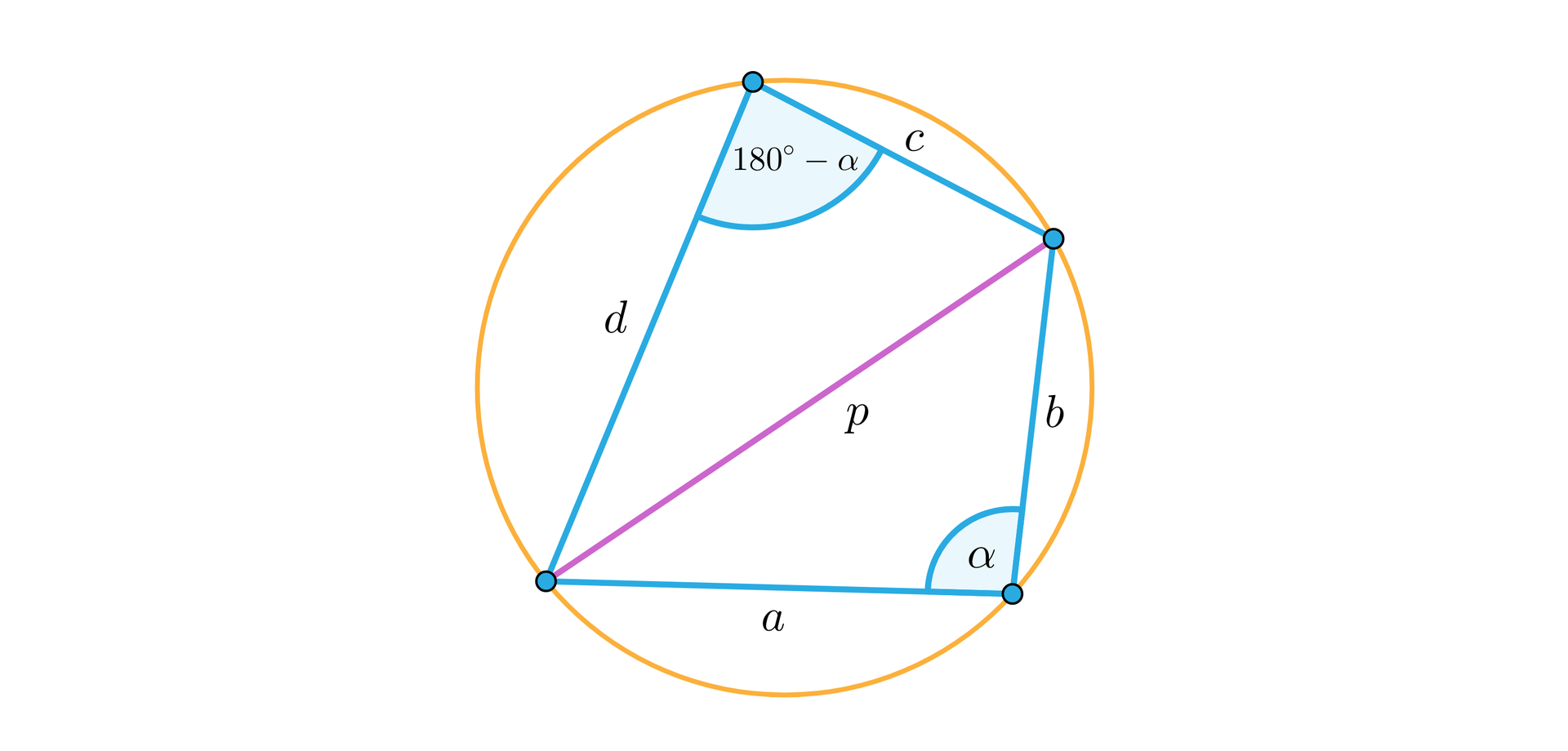
Ilustracja przedstawia czworokąt o bokach a b c d wpisany w okrąg. Zaznaczono przekątną o długości p. Pomiędzy ramieniem a i b jest kąt o mierze alfa. A pomiędzy ramieniem d i c jest kąt o mierze 180 stopni minus alfa. — Dowód wzoru Brahmagupty

Wtedy pole $P$ da się wyrazić jako sumę pól odpowiednich dwóch trójkątów:

$P = \frac{a b \sin α}{2} + \frac{c d \sin (180 ° - α)}{2} = \frac{(a b + c d) \sin α}{2}$ .

Stosując twierdzenie cosinusów do wyrażenia kwadratu długości przekątnej $p$ otrzymujemy zależność $p^{2} = a^{2} + b^{2} - 2 a b \cos α = c^{2} + d^{2} - 2 c d \cos (180 ° - α)$ , z której, po zastosowaniu wzoru redukcyjnego, wyznaczymy wartość $\cos α$ :

$\cos α = \frac{a^{2} + b^{2} - c^{2} - d^{2}}{2 (a b + c d)}$ .

Korzystając z jedynki trygonometrycznej otrzymujemy, że $\sin^{2} α = 1 - {[\frac{a^{2} + b^{2} - c^{2} - d^{2}}{2 (a b + c d)}]}^{2} = \frac{{[2 (a b + c d)]}^{2} - {[a^{2} + b^{2} - c^{2} - d^{2}]}^{2}}{4 {(a b + c d)}^{2}}$ .

Kolejne przekształcenia licznika otrzymanego ułamka będą opierały się na zastosowaniu wzorów skróconego mnożenia, w szczególności wzoru na różnicę kwadratów. Wtedy otrzymujemy kolejno:

${[2 (a b + c d)]}^{2} - {[a^{2} + b^{2} - c^{2} - d^{2}]}^{2} =$

$= [2 (a b + c d) - (a^{2} + b^{2} - c^{2} - d^{2})] \cdot [2 (a b + c d) + (a^{2} + b^{2} - c^{2} - d^{2})] =$

$= [(c^{2} + d^{2} + 2 c d) - (a^{2} + b^{2} - 2 a b)] \cdot [(a^{2} + b^{2} + 2 a b) - (c^{2} + d^{2} - 2 c d)] =$

$= [{(c + d)}^{2} - {(a - b)}^{2}] \cdot [{(a + b)}^{2} - {(c - d)}^{2}] =$

$= (b + c + d - a) (a + c + d - b) (a + b + d - c) (a + b + c - d)$

Podstawiając standardowe oznaczenie $p = \frac{a + b + c + d}{2}$ otrzymany iloczyn można zapisać w postaci

$(b + c + d - a) (a + c + d - b) (a + b + d - c) (a + b + c - d) =$

$= (a + b + c + d - 2 a) (a + b + c + d - 2 b) (a + b + c + d - 2 c) (a + b + c + d - 2 d) =$

$= (2 p - 2 a) (2 p - 2 b) (2 p - 2 c) (2 p - 2 d) = 16 (p - a) (p - b) (p - c) (p - d)$ .

Zatem

$P = \frac{(a b + c d) \sin α}{2} = \frac{(a b + c d)}{2} \sqrt{\frac{16 (p - a) (p - b) (p - c) (p - d)}{4 {(a b + c d)}^{2}}} =$

$= \sqrt{(p - a) (p - b) (p - c) (p - d)}$ .

Co należało wykazać.

Przykład 1

Okazuje się, że własności czworokąta cyklicznego można wykorzystać do badania własności pięciokąta foremnego.

Rozważmy pięciokąt foremny o boku długości $1$ , a jego przekątną oznaczmy przez
$p$ , jak na rysunku.

R1ecCgkHnb3Kr

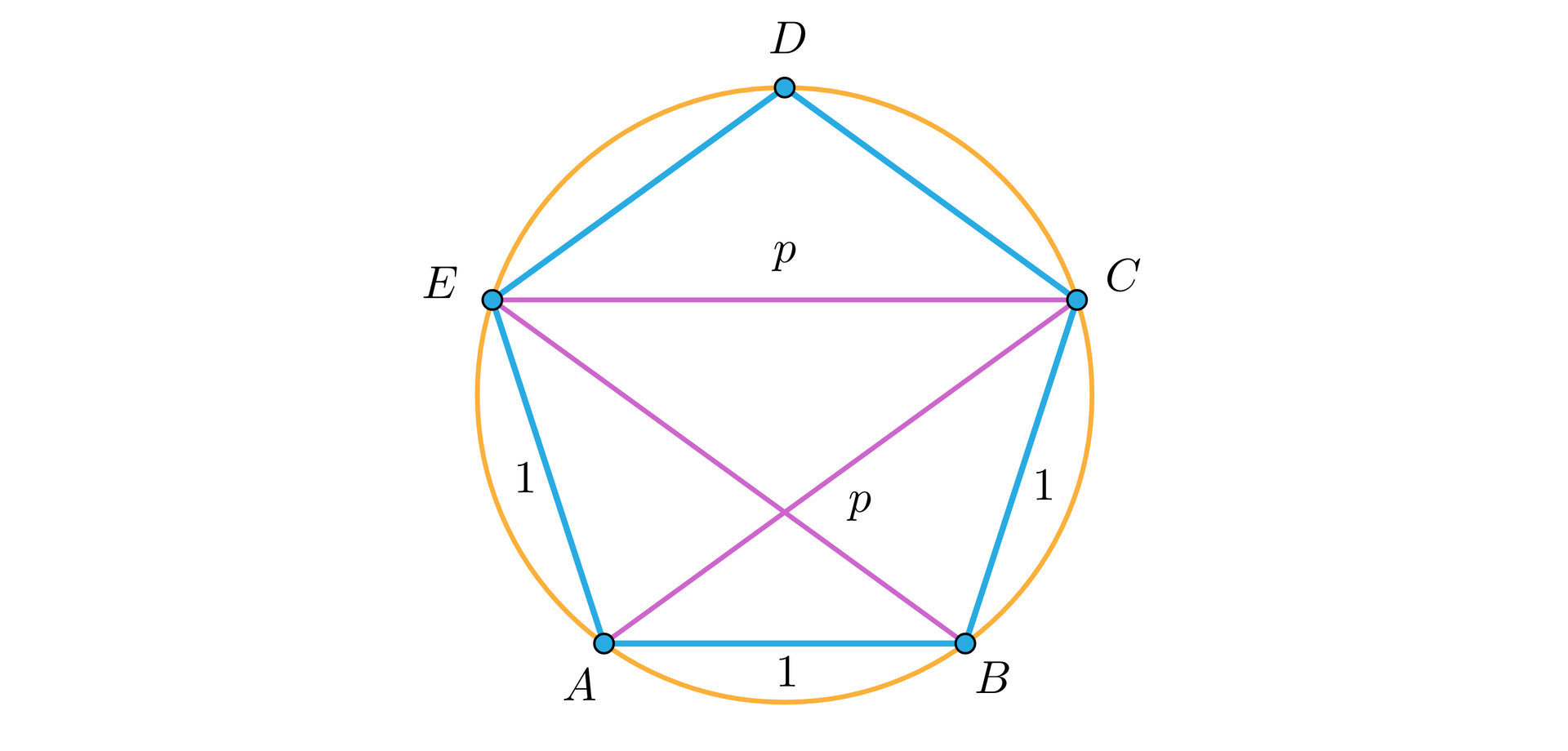
Ilustracja przedstawia pięciokąt foremny A B C D E o boku długości jeden wpisany w okrąg. Zaznaczono jego trzy przekątne o długości p: pierwsza to odcinek E C, druga to A C, trzecia to E B. — Pięciokąt foremny

Czworokąt $A B C E$ , którego wierzchołkami są wierzchołki danego pięciokąta jest cykliczny, można zatem zastosować do niego twierdzenie Ptolemeuszatwierdzenie Ptolemeuszatwierdzenie Ptolemeusza.

Mamy wtedy: $p^{2} = 1 \cdot p + 1 \cdot 1$ .

Jedynym dodatnim rozwiązaniem tego równania jest tzw. złota liczba: $p = \frac{1 + \sqrt{5}}{2}$ .

Skądinąd wiadomo, że kąt wewnętrzny pięciokąta foremnego ma miarę $108 °$ .

Stosując twierdzenie cosinusów moglibyśmy zapisać, że $p^{2} = 1^{2} + 1^{2} - 2 \cos 108 °$ .

Wynik jest oczywiście poprawny, ale nieco „uwikłany”.

Można go jednak wykorzystać, uwzględniając wcześniejszy rezultat, do obliczenia dokładnej wartości sinusa $18 °$ .

Mamy bowiem $p = \frac{1 + \sqrt{5}}{2} = \sqrt{2 - 2 \cos 108 °} = \sqrt{2 - 2 \cos (90 ° + 18 °)} = \sqrt{2 + 2 \sin 18 °}$ .

Stąd ${(\frac{1 + \sqrt{5}}{2})}^{2} = 2 + 2 \sin 18 °$ , czyli $\sin 18 ° = \frac{\sqrt{5} - 1}{4}$ .

Słownik

wielokąt cykliczny

wielokątem cyklicznym nazywamy wielokąt wypukły, który da się wpisać w okrąg

twierdzenie Ptolemeusza

twierdzenie, które orzeka, że czworokąt o kolejnych bokach długości $a$ , $b$ , $c$ , $d$ i przekątnych $p$ , $q$ jest cykliczny wtedy i tylko wtedy, gdy

p q = a c + b d

Wprowadzenie

Aplet

Czworokąt wpisany w okrąg i trójkąty

Słownik