Przeczytaj

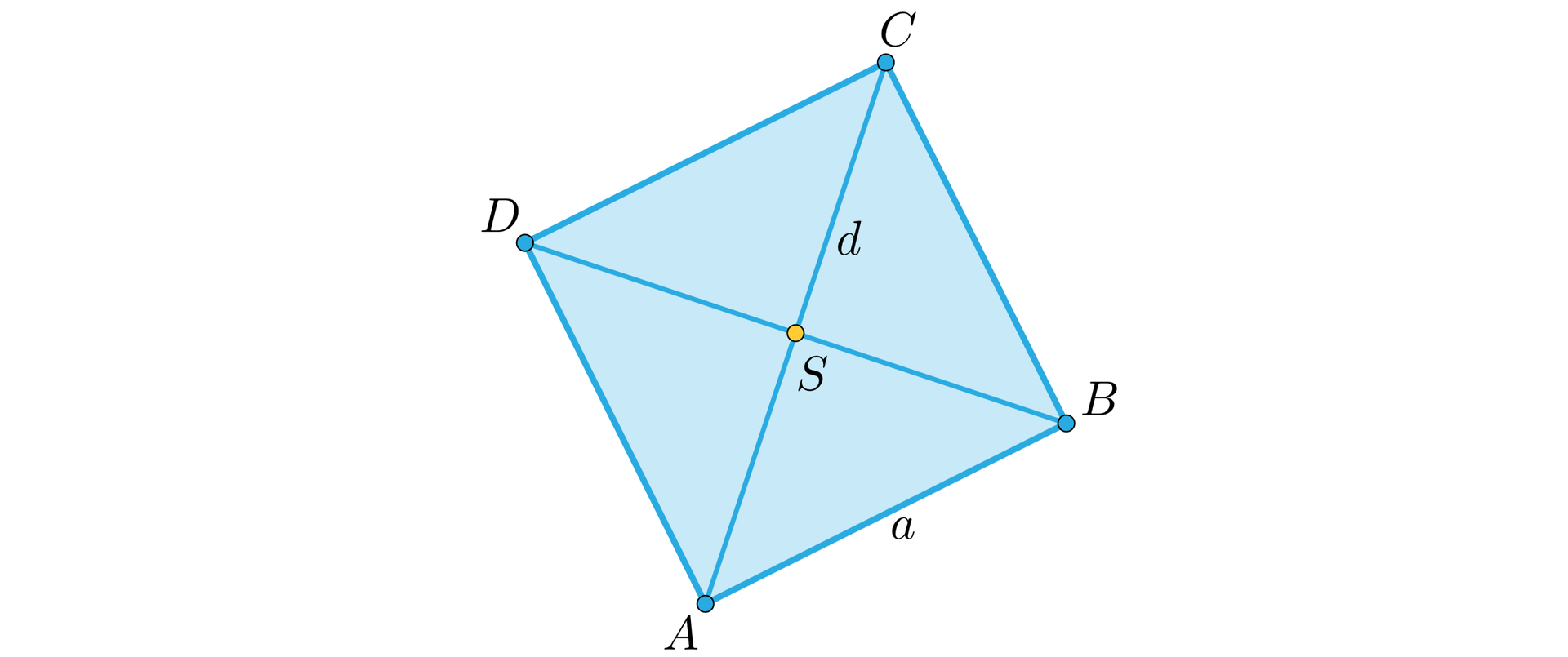
Kwadrat jest czworokątem, który ma wszystkie boki równe i wszystkie kąty proste. Przekątne kwadratu przecinają się pod kątem prostym i dzielą się w połowie. W naszych rozważaniach będziemy stosowali oznaczenia przedstawione na rysunku.

R1J3S3LNk8f6u

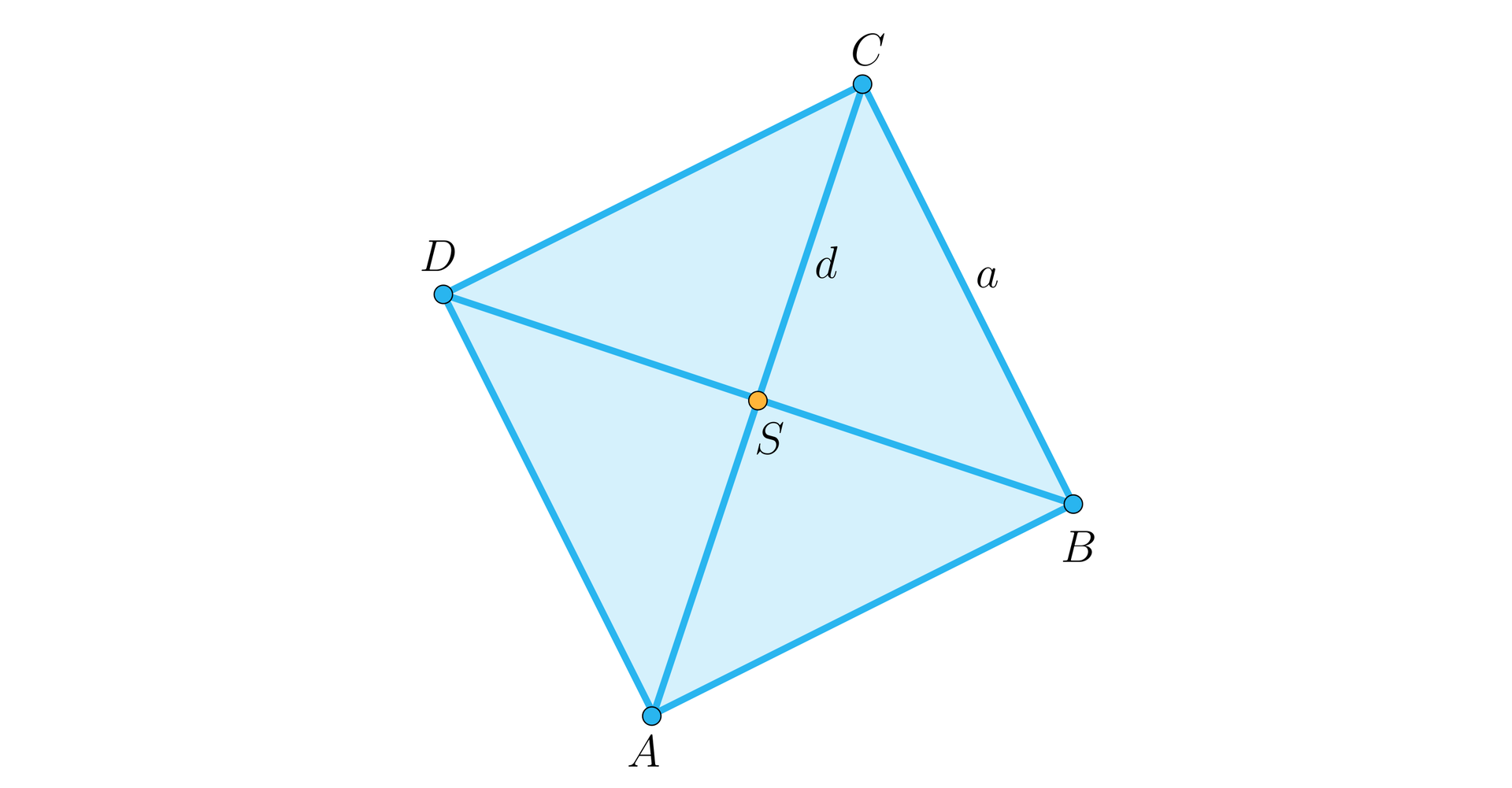
Ilustracja przedstawia kwadrat ABCD o boku a. Przekątne o długości d przecinają się w punkcie S.

Bok kwadratu $A B C D$ oznaczony jest symbolem $a$ , który oznacza też długość tego boku. Punkt $S$ jest punktem przecięcia przekątnych, $d$ oznacza przekątną (i jej długość). Symbolem $P$ oznaczamy pole kwadratu $A B C D$ .

Na początek zajmiemy się problemem mierzenia. Problem mierzenia w starożytności był bardzo trudnym zadaniem, gdyż nie znano pojęcia liczb rzeczywistych, a co za tym idzie nie stosowano wzorów takich jak $P = a^{2}$ . Problem zmierzenia pola figury sprowadzano do porównywania z figurami, których pole było znane.

Spróbujmy zastosować sposób myślenia starożytnych do wyznaczenia pola kwadratu. Przyjmujemy założenie, że pole kwadratu o boku długości równej jednej jednostce (czyli $1 j$ ) jest równe $1 j^{2}$ , czyli jedna jednostka kwadratowa. Pole to będziemy nazywali polem jednostkowym i będzie to wzorzec, do którego będziemy odnosić pozostałe wyliczenia.

Pokażemy, jak wyznaczać pole kwadratu w zależności od tego jaką liczbą jest długość boku kwadratu, począwszy od liczb naturalnych, potem odwrotności liczb naturalnych, następnie liczb wymiernych, by ostatecznie wyprowadzić wzór na pole kwadratu o boku długości rzeczywistej.

Dowody dotyczące pola figur opierają się na następujących własnościach pola.

Własności pola

Własność: Własności pola

Niech $P_{F}$ oznacza pole figury $F$ . Wtedy:

figury przystające mają równe pola;

jeżeli figura $F_{1}$ jest zawarta w figurze $F_{2}$ to $P_{F_{1}} \leq P_{F_{2}}$ ;

jeżeli $F_{1}$ , $F_{2}$ są rozłączne, to pole ich sumy jest równe sumie pól. Prawdziwa jest też ogólniejsza własność, że pole sumy figur jest równe sumie ich pól odjąć pole ich części wspólnej.

Pole kwadratu o boku długości $n$ , gdzie $n$ jest liczbą naturalną

Weźmy kwadrat o boku $a = n$ jednostek. Podzielmy dwa sąsiednie boki kwadratu na $n$ równych odcinków. Zadanie to można wykonać konstrukcyjnie przy pomocy cyrkla i linijki bez podziałki. Łączymy punkty podziału boków odcinkami równoległymi do boków, tak jak na przykładowym rysunku dla $n = 5$ .

R1e1vEjehydLr

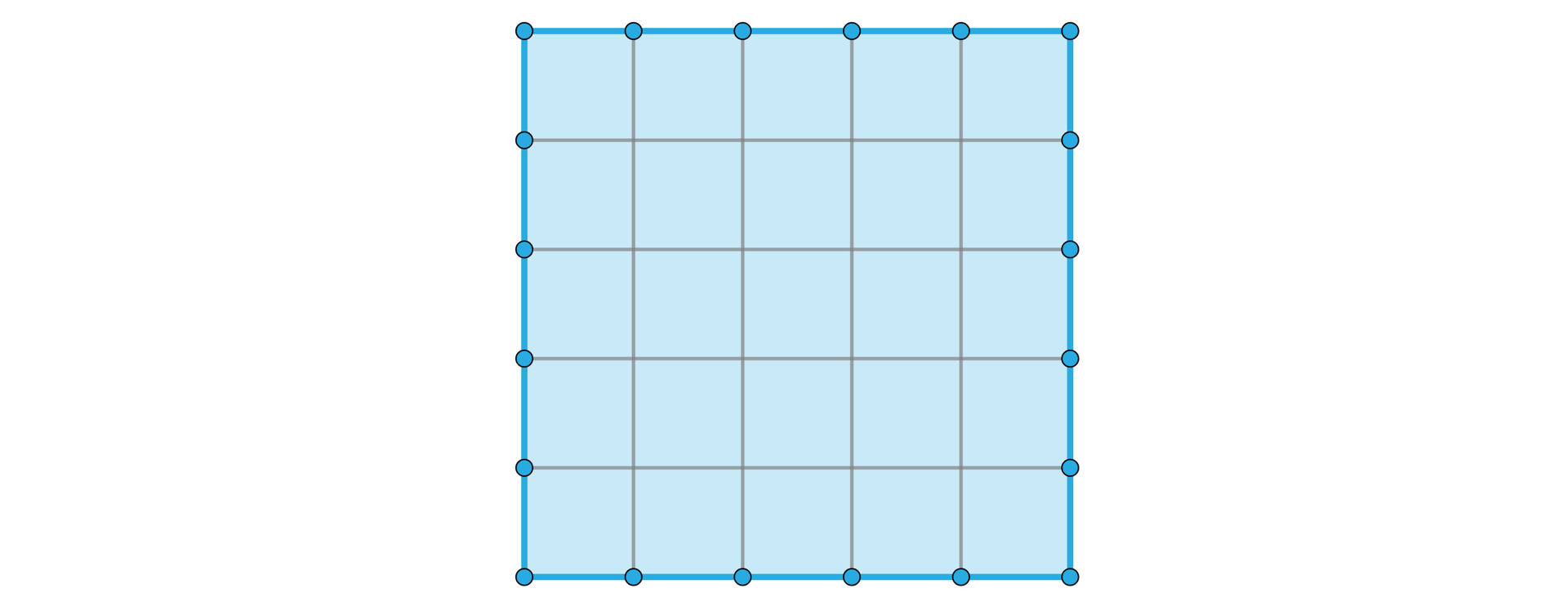
Ilustracja przedstawia kwadrat podzielony na 25 małych kwadratów.

Ponieważ odcinki poprowadzono równolegle do boków, to czworokąty otrzymane w ten sposób mają wszystkie kąty proste. Poza tym boki zostały podzielone na $n$ równych odcinków to każdy z otrzymanych czworokątów ma wszystkie boki równe o długości $1 j$ . To oznacza, że kwadrat o boku $n$ został podzielony na kwadraty o polu jednostkowym.

Do wyznaczenia pola $P$ wystarczy policzyć, ile jest kwadratów jednostkowych.

Zauważamy, że w wyniku podziału jednego z boków kwadratu na $n$ części otrzymujemy $n$ rzędów, a w wyniku podziału drugiego boku na $n$ równych części dostajemy $n$ kwadratów jednostkowych w każdym rzędzie. Ostatecznie kwadrat został podzielony na $n \cdot n = n^{2}$ kwadratów jednostkowych, więc jego pole $P$ jest sumą pól tych kwadratów i w efekcie $P = n^{2}$ jednostek kwadratowych.

Uwaga!

W dalszej części tego materiału będziemy zakładać, że jednostka jest ustalona i będziemy pomijać odniesienie jednostki tam, gdzie to nie prowadzi do nieporozumień.

Przykład 1

Wyznaczymy pole kwadratu o boku $8$ .

Rozwiązanie

Dzielimy kwadrat jak na poniższym rysunku.

RM0LvwoMega2n

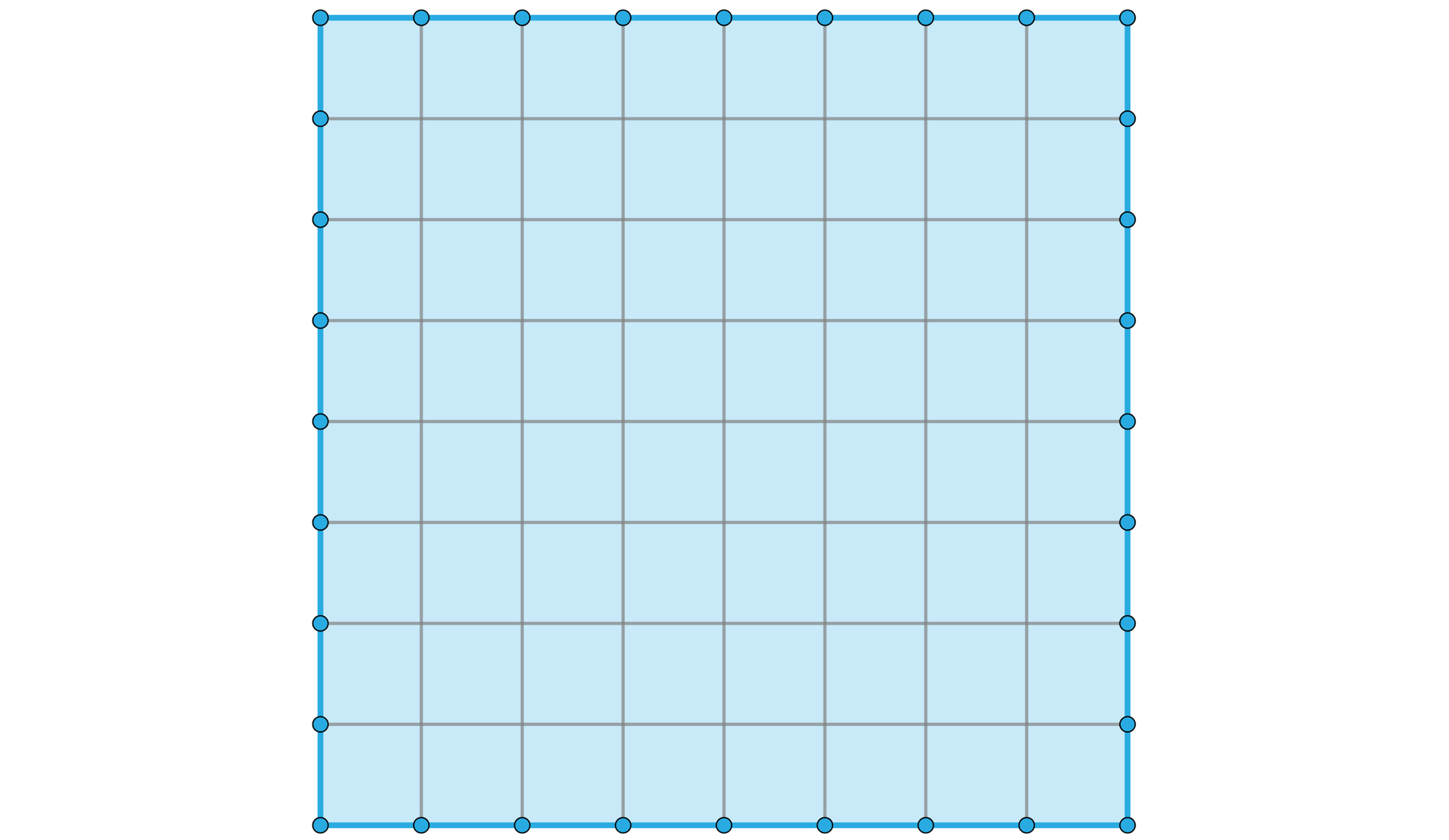
Ilustracja przedstawia kwadrat podzielony na 64 małych kwadratów.

Dostajemy $8$ rzędów po $8$ kwadratów w każdym, więc pole kwadratu o boku $8$ jest równe $64$ jednostki kwadratowe.

Zauważmy, że wzór na pole został już wyprowadzony, więc $P = 8^{2} = 64$ .

Pole kwadratu o boku długości $\frac{1}{n}$ , gdzie $n$ jest liczbą naturalną

Chcemy wyznaczyć pole kwadratu o boku $a = \frac{1}{n}$ .

Podzielmy każdy bok kwadratu jednostkowego na $n$ równych części, a następnie metodą opisaną wyżej na $n^{2}$ przystających kwadratów o boku $a = \frac{1}{n}$ . Ponieważ pole kwadratu jednostkowego jest równe $1$ , to pole każdego z tak uzyskanych kwadratów jest równe $a = \frac{1}{n^{2}}$ .

Ostatecznie wzór na pole kwadratu o boku $a = \frac{1}{n}$ jest następujący:

P = \frac{1}{n^{2}} = {(\frac{1}{n})}^{2}

Przykład 2

Wyznaczymy pole kwadratu o boku $\frac{1}{3}$ .

Rozwiązanie

Po zastosowaniu wzoru pole kwadratu o boku $a = \frac{1}{n}$ mamy $P = \frac{1}{3^{2}} = \frac{1}{9}$ .

Gdybyśmy chcieli sami wyznaczyć pole tego kwadratu bez odwoływania się do wzoru, to kwadrat jednostkowy należy podzielić na $9$ przystających kwadratów metodą opisaną wyżej. Pole kwadratu o boku $\frac{1}{3}$ jest polem jednego z tych dziewięciu kwadratów, więc jest równe $\frac{1}{9}$ .

Pole kwadratu o boku długości wymiernej

Chcemy wyznaczyć pole kwadratu o boku wymiernym, czyli $a = \frac{m}{n}$ , gdzie $m$ , $n$ są liczbami naturalnymi.

Metodą opisaną wyżej konstruujemy kwadrat o boku $\frac{1}{n}$ . Jego pole jest równe $\frac{1}{n^{2}}$ .

Układamy kwadraty o boku $\frac{1}{n}$ w $m$ rzędach, po $m$ kwadratów w każdym rzędzie.

W ten sposób powstał kwadrat o boku $\frac{m}{n}$ . Składa się on z $m^{2}$ kwadratów o polu $\frac{1}{n^{2}}$ .

Ostatecznie $P = \frac{m^{2}}{n^{2}} = {(\frac{m}{n})}^{2}$ .

Pole kwadratu o boku długości niewymiernej – dla zainteresowanych

Chcemy wyznaczyć pole kwadratu o boku $a$ , gdzie $a$ jest liczbą niewymierną.

Każda liczba niewymierna ma nieskończone rozwinięcie dziesiętne $a = c_{0}, c_{1} c_{2} c_{3}$ ...

Jeżeli utniemy tę liczbę na $n$ -tym miejscu po przecinku to dostaniemy $a_{n} = \frac{c_{0} c_{1} . . . c_{n}}{10^{n}}$ .

Liczbę $a_{n}$ nazywamy $n$ -tym reduktem liczby $a$ . Licznik $n$ -tego reduktu $c_{0} c_{1} . . . c_{n}$ oznaczamy symbolem $l_{n}$ .

Przykład 3

Wyznaczymy kilka początkowych reduktów liczby $a = \sqrt{3}$ .

Rozwiązanie

Rozwinięcie dziesiętne tej liczby jest postaci $1, 7320508$ .

Wtedy

$a_{0} = 1$ , $a_{1} = \frac{17}{10}$ , $a_{2} = \frac{173}{100} = \frac{173}{10^{2}}$ , $a_{3} = \frac{1732}{10^{3}}$ , $a_{4} = \frac{17320}{10^{4}}$ , $a_{5} = \frac{173205}{10^{5}}$ , $a_{6} = \frac{1732050}{10^{3}}$ ,...

$l_{0} = 1$ , $l_{1} = 17$ , $l_{2} = 173$ , $l_{3} = 1732$ , $l_{4} = 17320$ , $l_{5} = 173205$ , $l_{6} = 1732050$ ,...

Ograniczenie liczby

a

przez jej redukt

Własność: Ograniczenie liczby

a

przez jej redukt

Jeśli liczba $a$ ma nieskończone rozwinięcie dziesiętne, to dla dowolnej liczby naturalnej $n$ zachodzi nierówność $a_{n} < a < \frac{l_{n} + 1}{10^{n}} = a_{n} + \frac{1}{10^{n}}$ .

Wróćmy teraz do problemu wyznaczenia pola kwadratu o boku $a$ .

RyqPd5E38ogzk

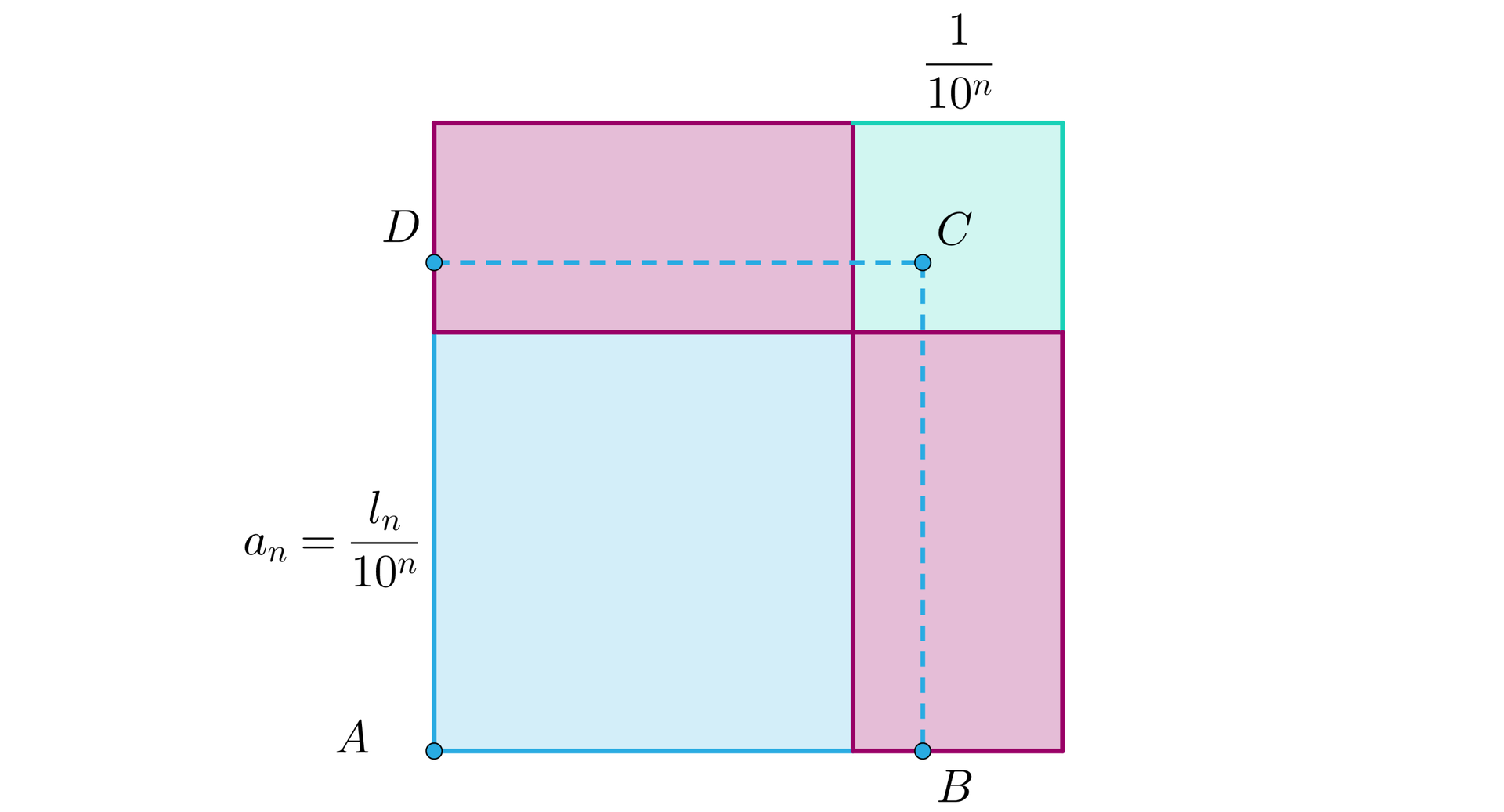
Ilustracja przedstawia kwadrat składający się z czterech figur. Niebieskiego kwadratu o boku an=ln10n. Dwóch różowych prostokątów o boku an=ln10n oraz 110n. I z zielonego kwadratu o boku 110n.

Dla dowolnego $n$ pole $P$ kwadratu $A B C D$ jest większe od pola kwadratu o boku $a_{n}$ oraz jest mniejsze od pola kwadratu o boku $a_{n} + \frac{1}{10^{n}}$ .

Boki tych kwadratów są liczbami wymiernymi.

W ten sposób pole $P$ wyznaczone jest w przybliżeniu. Dokładność tego przybliżenia jest różnicą między polami kwadratów ograniczających kwadrat $A B C D$ .

Na rysunku widać, że różnica ta, to suma pól dwóch czerwonych (przystających) prostokątów o bokach $a_{n}$ i $\frac{1}{10^{n}}$ oraz kwadratu o boku $\frac{1}{10^{n}}$ .

Różowy prostokąt składa się z $l_{n}$ kwadratów o boku $\frac{1}{10^{n}}$ , więc pole różowego prostokąta jest równe $\frac{l_{n}}{10^{2 n}}$ .

Stąd dokładność przybliżenia wynosi $r_{n} = \frac{2 l_{n}}{10^{2 n}} + \frac{1}{10^{2 n}} = \frac{2 a_{n}}{10^{n}} + \frac{1}{10^{2 n}}$ .

Stąd w przybliżeniu pole $P$ jest równe $P \approx a_{n}^{2} + r_{n}$ .

Teraz zauważmy, że przy $n$ dążącym do nieskończoności $a_{n}^{2}$ zbiega do $a^{2}$ a $r_{n}$ zbiega do zera.

Zatem w granicy dostajemy $P = a^{2}$ .

o polu kwadratu

Twierdzenie: o polu kwadratu

Pole kwadratu o boku $a$ jest równe $P = a^{2}$ .

Wykorzystanie podobieństwa kwadratów do wyznaczenia pola kwadratu o boku $a$

Innym sposobem wyznaczenia wzoru na pole kwadratu jest zastosowanie podobieństwa kwadratów. Ponieważ wszystkie kwadraty są do siebie podobne, to kwadrat o boku $a$ jest podobny do kwadratu jednostkowego w skali $k = a$ . Z własności pola figur podobnych wynika, że jego pole $P$ jest równe $P = k^{2} \cdot 1 = a^{2}$ .

Przykład 4

Kwadrat $K$ jest podobny do kwadratu jednostkowego w skali $k = \frac{3}{4}$ a kwadrat $L$ jest podobny do kwadratu $K$ w skali $l = 6$ . Wyznaczymy bok i pole kwadratu $K$ i kwadratu $L$ .

Rozwiązanie

Z podobieństwa wynika, że bok kwadratu $K$ jest równy $a = \frac{3}{4}$ a pole kwadratu $K$ jest równe $k^{2} \cdot 1 = \frac{9}{16}$ .

Podobnie, bok kwadratu $L$ jest równy $l \cdot a = \frac{6 \cdot 3}{4} = \frac{9}{2}$ . Po zastosowaniu wzoru na pole kwadratu dostajemy, że pole kwadratu $L$ jest równe ${(\frac{9}{2})}^{2} = \frac{81}{4}$ .

Sprawdzimy teraz, czy nie popełniliśmy błędu w wyliczeniach wyznaczając pole kwadratu $L$ w inny sposób – wykorzystując skalę podobieństwa.

Pole kwadratu $L$ jest równe $l^{2} \cdot P = 6^{2} \cdot \frac{9}{16} = \frac{36 \cdot 9}{16} = \frac{81}{4}$ .

Dwa sposoby wyliczenia pola doprowadziły do tego samego wyniku.

Wzory skróconego mnożenia

Udowodnimy wzory na kwadrat sumy i różnicy wykorzystując pole kwadratu.

Wzory skróconego mnożenia

Twierdzenie: Wzory skróconego mnożenia

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

Dowód

1. Popatrzmy na rysunek, na którym przedstawiono kwadrat o boku $a + b$ .

R11nnJLNOTvos

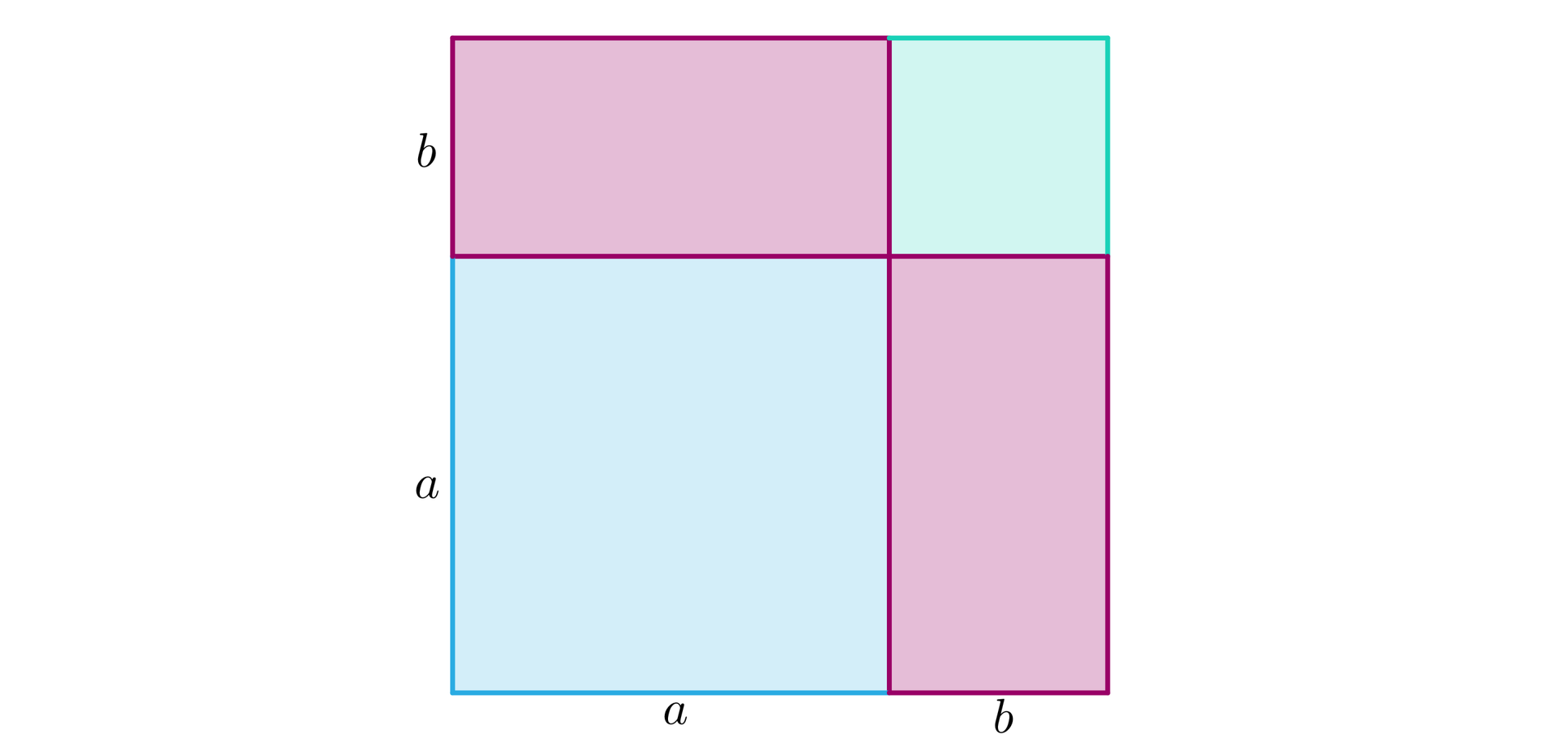
Ilustracja przedstawia kwadrat składający się z czterech figur. Niebieskiego kwadratu o boku a, dwóch różowych prostokątach o boku a i b oraz z zielonego kwadratu o boku b.

Prowadzimy linie równoległe do boków tego kwadratu, tak, żeby odciąć kwadrat o boku $A$ .

Wtedy pole kwadratu $P$ o boku $a + b$ jest równe sumie pól następujących czworokątów: niebieski kwadrat o boku $a$ , zielony kwadrat o boku $b$ i dwa różowe prostokąty o bokach $a$ i $b$ .

Stąd $P = {(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

2. Do dowodu wzoru na kwadrat różnicy zakładamy, że $a > b$ i wykonujemy rysunek analogiczny do poprzedniego. Duży kwadrat ma bok $a$ , niebieski kwadrat ma bok $a - b$ , a zielony ma bok $b$ . Bierzemy jeszcze pod uwagę dwa prostokąty o bokach $a$ i $b$ .

R1SCSXjSEqvvO

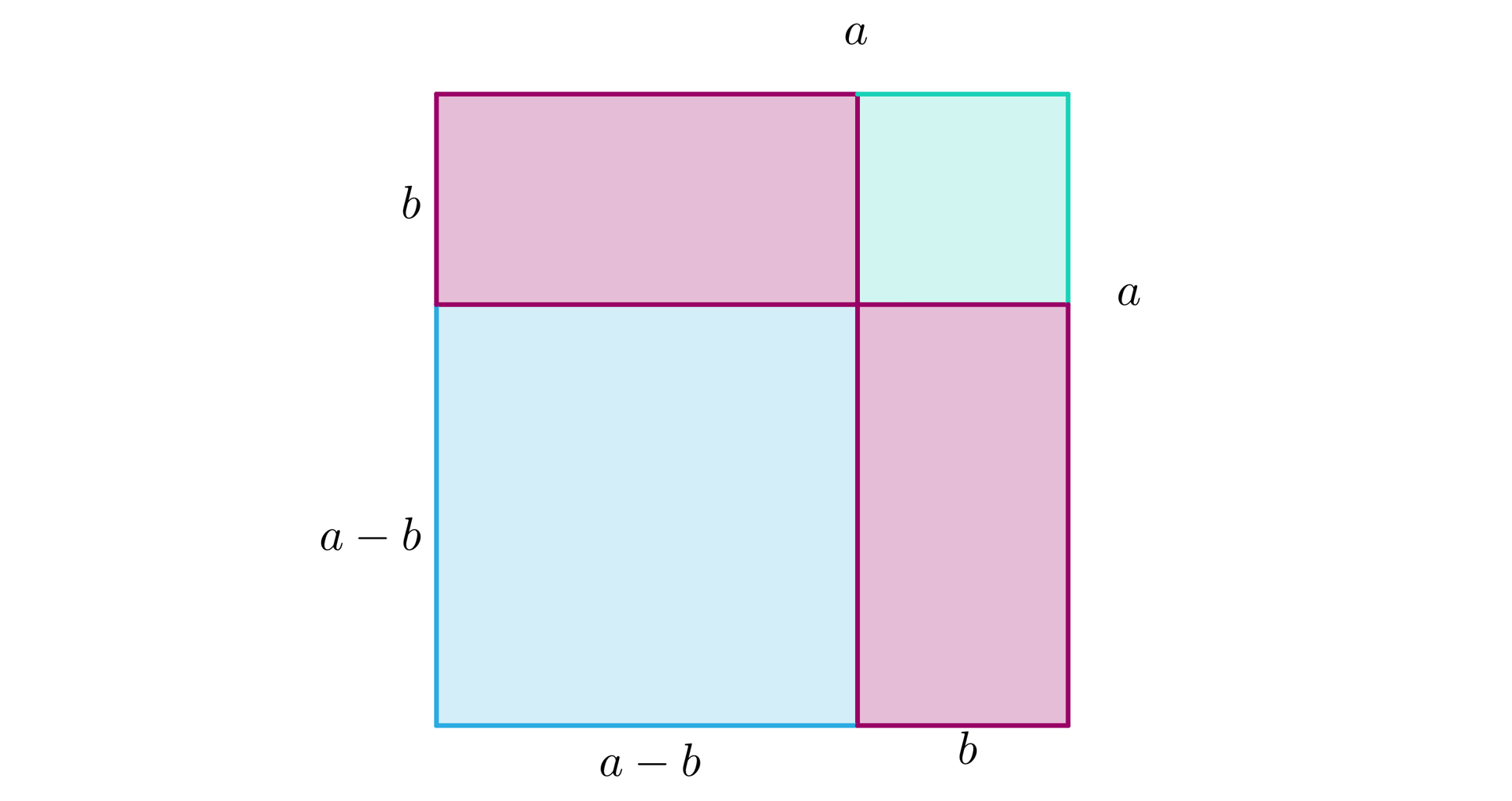
Ilustracja przedstawia kwadrat składający się z czterech figur. Niebieskiego kwadratu o boku a minus b, dwóch różowych prostokątach o bokach a minus b oraz b i z zielonego kwadratu o boku a.

Aby dostać pole $P$ kwadratu o boku $a - b$ odejmujemy od pola kwadratu o boku $a$ pola dwóch prostokątów o bokach $a$ i $b$ , ale te prostokąty mają część wspólną – kwadrat o boku $b$ , którego pole musimy dodać.

Stąd $P = {(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ .

Pole kwadratu, którego wierzchołki mają całkowite współrzędne

Jeśli podane są współrzędne dwóch sąsiednich wierzchołków kwadratu $A = (a_{x}, a_{y})$ , $B = (b_{x}, b_{y})$ to długość boku $A B$ jest równa $a = \sqrt{{(a_{x} - b_{x})}^{2} + {(a_{y} - b_{y})}^{2}}$ .

Jeśli podane są współrzędne dwóch przeciwległych wierzchołków kwadratu $A = (a_{x}, a_{y})$ , $C = (c_{x}, c_{y})$ , to długość przekątnej $A C$ jest równa $c = \sqrt{{(a_{x} - c_{x})}^{2} + {(a_{y} - c_{y})}^{2}}$ .

Pole kwadratu, którego dwa wierzchołki mają współrzędne $(a_{x}, a_{y})$ i $(b_{x}, b_{y})$ jest równe:

$P = {(a_{x} - b_{x})}^{2} + {(a_{y} - b_{y})}^{2}$ jeśli wierzchołki te są wierzchołkami sąsiednimi;

$P = \frac{{(a_{x} - b_{x})}^{2} + {(a_{y} - b_{y})}^{2}}{2}$ jeśli wierzchołki te są wierzchołkami przeciwległymi.

Przykład 5

Dane są $3$ wierzchołki kwadratu $K = (4, 6)$ , $L = (- 1, 5)$ , $M = (0, 0)$ . Wyznaczymy jego pole.

Rozwiązanie

Wystarczy wybrać parę wierzchołków, które są sąsiednie lub parę wierzchołków, które są przeciwległe i zastosować powyższe twierdzenie.

W tym celu wyznaczamy długości odcinków $K L$ i $L M$ . Jeśli długości są równe, to $K$ , $L$ są wierzchołkami sąsiednimi. Jeśli długości nie są równe, to wierzchołki krótszego są sąsiednie.

$|K L| = \sqrt{{(4 - (- 1))}^{2} + {(6 - 5)}^{2}} = \sqrt{25 + 1} = \sqrt{26}$

$|L M| = \sqrt{{(- 1 - 0)}^{2} + {(5 - 0)}^{2}} = \sqrt{1 + 25} = \sqrt{26}$

Stąd pole kwadratu jest równe ${(\sqrt{26})}^{2} = 26$ .

o polu kwadratu, którego dwa sąsiednie wierzchołki mają współrzędne całkowite

Twierdzenie: o polu kwadratu, którego dwa sąsiednie wierzchołki mają współrzędne całkowite

Jeśli współrzędne $A = (a_{x}, a_{y})$ , $B = (b_{x}, b_{y})$ dwóch sąsiednich wierzchołków kwadratu są liczbami całkowitymi, to pole kwadratu jest też liczbą całkowitą. Własność ta nie zachodzi dla wierzchołków przeciwległych.

Dowód

$P = {(a_{x} - b_{x})}^{2} + {(a_{y} - b_{y})}^{2}$ jeśli wierzchołki te są wierzchołkami sąsiednimi. Korzystając z faktu, że suma i różnica oraz kwadrat liczb całkowitych są liczbami całkowitymi dostajemy, że $P$ jest liczbą całkowitą.

Przykład 6

Pokażemy przykład dwóch przeciwległych wierzchołków kwadratu, które mają współrzędne całkowite, ale pole kwadratu nie jest liczbą całkowitą.

Rozwiązanie

Weźmy punkty $A = (2, 4)$ i $C = (5, 4)$ , które są przeciwległymi wierzchołkami kwadratu. Wtedy $P = \frac{{(2 - 5)}^{2} + {(4 - 4)}^{2}}{2} = \frac{9}{2}$ .

Punktami kratowymipunkty kratowePunktami kratowymi nazywamy punkty o współrzędnych całkowitych.

Prawdziwe jest twierdzenie Picka, które mówi o polu wielokąta, którego wierzchołkami są punkty kratowe.

Picka

Twierdzenie: Picka

Pole wielokąta, którego wierzchołkami są punkty kratowe jest równe $P = ω + \frac{δ}{2} - 1$ , gdzie $ω$ jest liczbą punktów kratowych należących do wnętrza wielokąta a $δ$ jest liczbą punktów kratowych należących do brzegu wielokąta.

Przykład 7

Obliczymy pole kwadratu $K$ przedstawionego na rysunku, stosując twierdzenie Picka oraz wyznaczając pole kwadratu z użyciem twierdzenia Pitagorasa potwierdzimy wynik.

RWImcC5LyyoZt

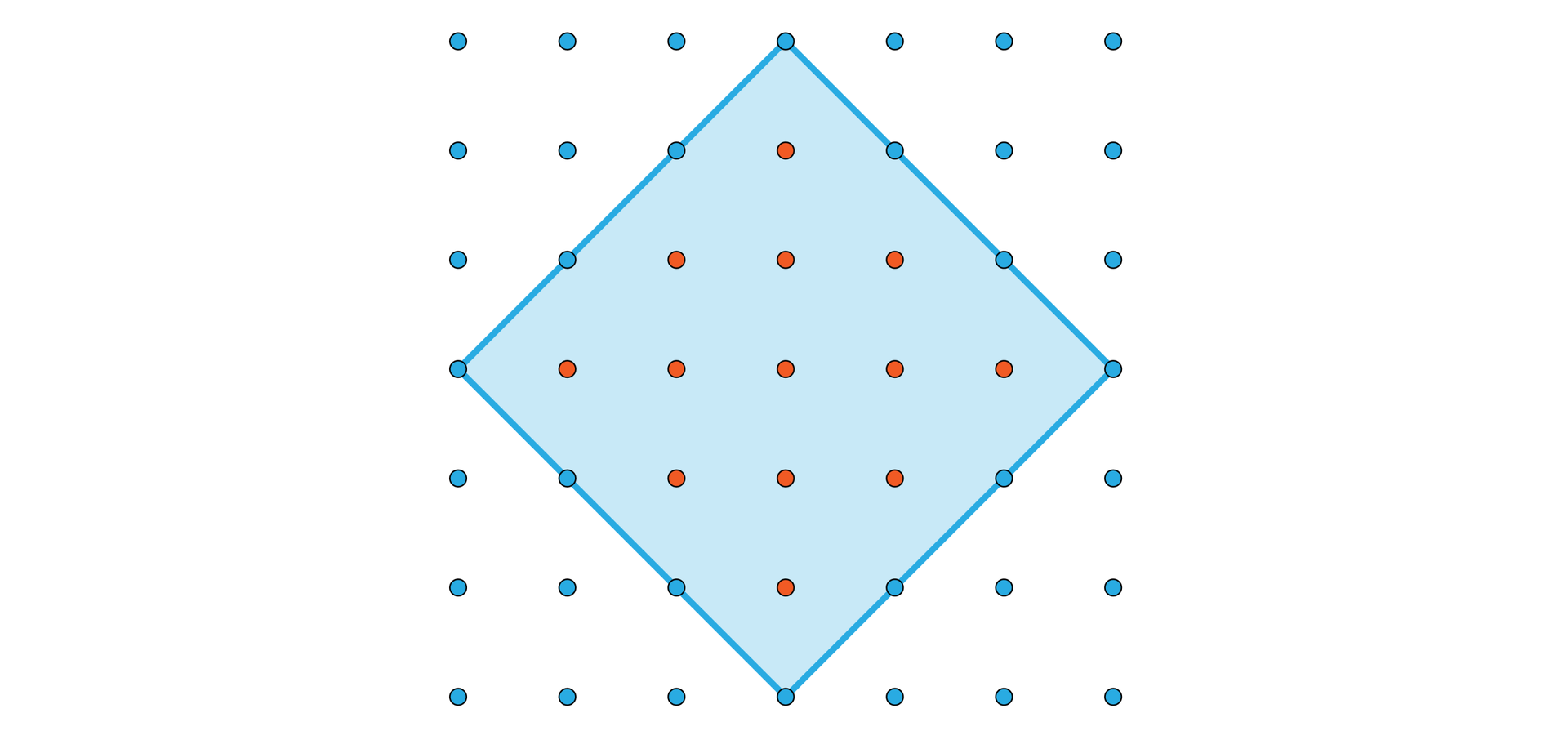
Ilustracja przedstawia 49 punktów. W jego środku umieszczono kwadrat o boku 4 kropek.

Rozwiązanie

Wewnątrz kwadratu jest $13$ punktów kratowych, a na brzegu jest $12$ punktów kratowych. Stąd $P = 13 + \frac{12}{2} - 1 = 18$ .

Policzymy teraz długość boku kwadratu $K$ patrząc na punkty kratowe. Dla dowolnego boku kwadratu budujemy kwadrat, dla którego ten bok jest przekątną. Ten nowy kwadrat ma bok długości $3$ , więc jego przekątna ma długość $3 \sqrt{2}$ .

Stad pole kwadratu $P = {(3 \sqrt{2})}^{2} = 18$ . Obydwie metody doprowadziły do tego samego wyniku.

Wykorzystanie przekątnej do wyznaczania pola kwadratu

Długość $d$ przekątnej kwadratu o boku $a$ można wyznaczyć z twierdzenia Pitagorasa w następujący sposób:

R1ZJzXRabasoP

{(\frac{d}{2})}^{2} + {(\frac{d}{2})}^{2} = a^{2}

\frac{2 \cdot d^{2}}{4} = a^{2}

2 d^{2} = 4 a^{2}

d = a \sqrt{2}

Stąd też można wyznaczyć długość boku z długości przekątnej $a = \frac{d}{\sqrt{2}}$ .

o polu kwadratu z wykorzystaniem przekątnej

Twierdzenie: o polu kwadratu z wykorzystaniem przekątnej

Pole kwadratu o przekątnej $d$ jest równe $P = \frac{d^{2}}{2}$ .

Dowód

$P = a^{2} = {(\frac{d}{\sqrt{2}})}^{2} = \frac{d^{2}}{2}$

Przykład 8

Na rysunku przekątna kwadratu $I J F G$ ma długość $8$ .

R1ajM2gVncZps

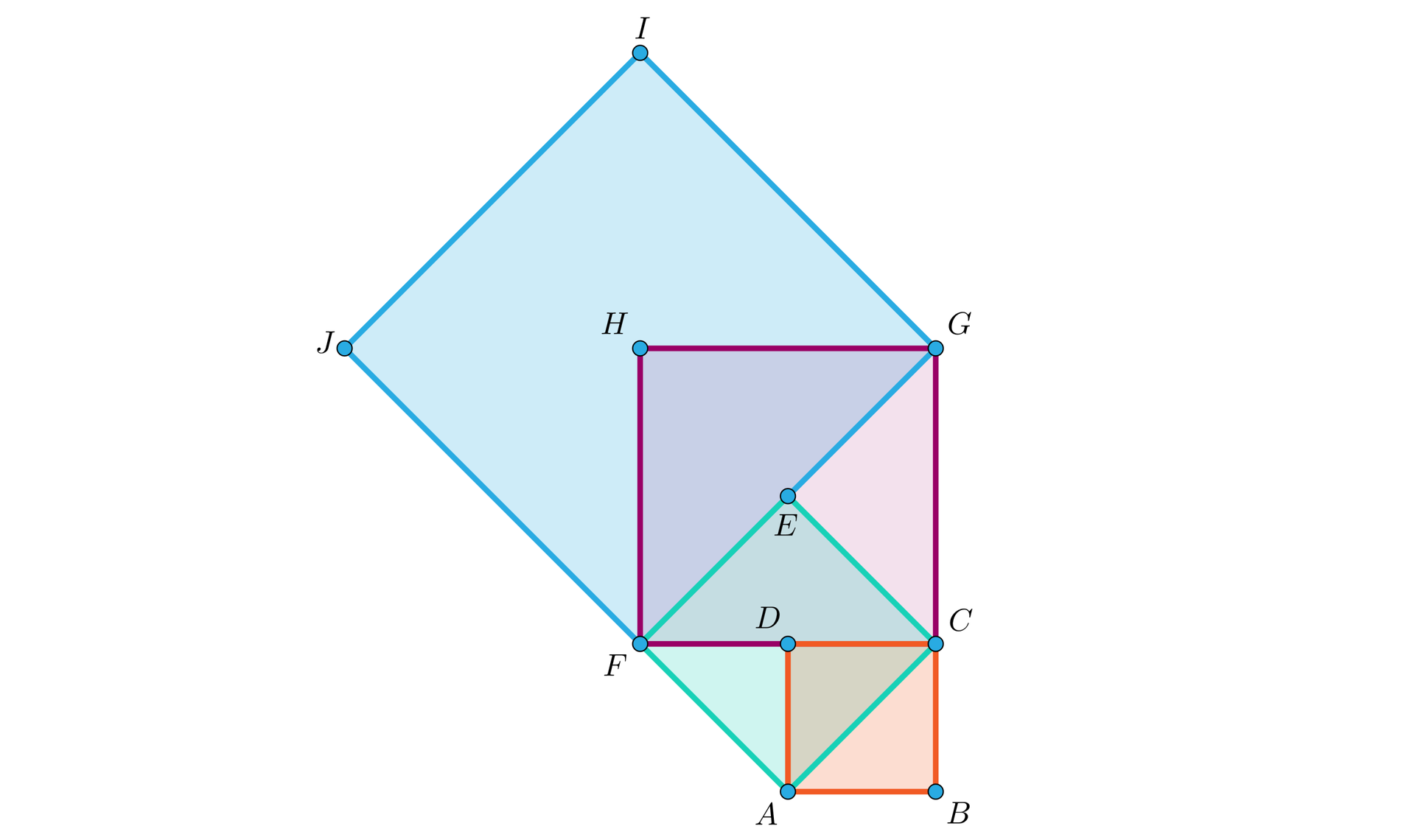
Ilustracja przedstawia kwadrat ABCD. Do boku DC przyłączono kwadrat CGHF. Do wierzchołka F dołączono dwa kwadraty. Jeden kwadrat ACEF o środku D oraz FGIJ o środku H.

Wyznaczymy pola i długości boków wszystkich kwadratów na rysunku.

Rozwiązanie

$P_{I J F G} = \frac{8^{2}}{2} = 32$ , $|I J| = \frac{8}{\sqrt{2}} = \frac{8 \sqrt{2}}{2} = 4 \sqrt{2}$

Bok kwadratu $I J F G$ jest przekątną kwadratu $C F H G$ , więc $P_{C F H G} = \frac{{(4 \sqrt{2})}^{2}}{2} = 16$ , $|H F| = \frac{4 \sqrt{2}}{\sqrt{2}} = 4$ .

$P_{A C E F} = \frac{4^{2}}{2} = 8$ , $|F E| = \frac{4}{\sqrt{2}} = \frac{4 \sqrt{2}}{2} = 2 \sqrt{2}$

$P_{A B C D} = \frac{{(2 \sqrt{2})}^{2}}{2} = 4$ , $|A B| = \frac{2 \sqrt{2}}{\sqrt{2}} = 2$

Zauważmy, że pole kolejnego kwadratu jest połową pola kwadratu poprzedniego. Stąd można wyznaczyć skalę podobieństwa kolejnego kwadratu do kwadratu poprzedniego

$k = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}}$ .

Przykład 9

Wyznaczymy pole kwadratu wpisanego w okrąg o promieniu $r$ .

RZINg9ItRYpFf

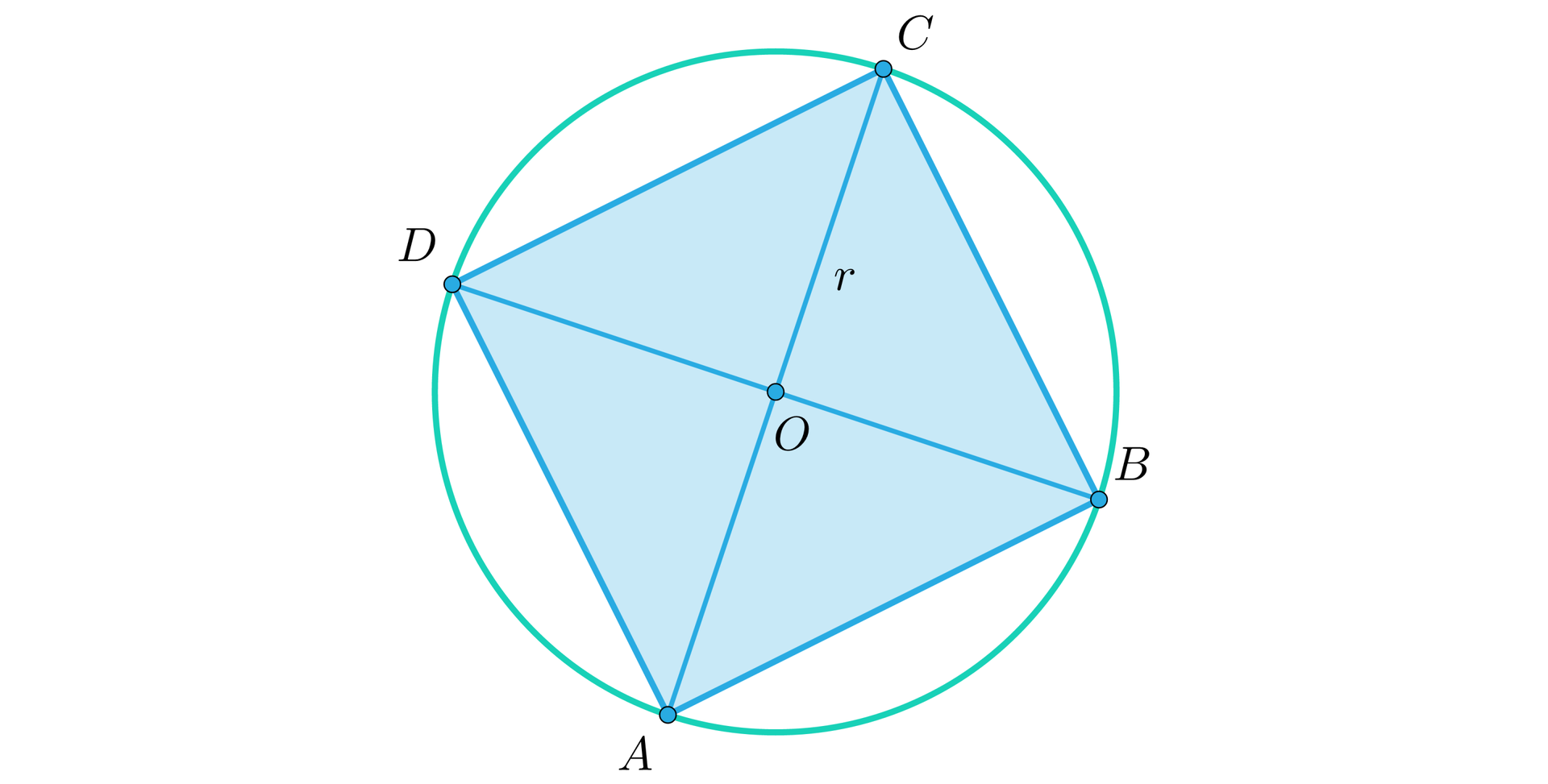
Ilustracja przedstawia kwadrat ABCD wpisany w okrąg o promieniu r. Przekątne kwadratu przecinają się w punkcie O.

Rozwiązanie

Średnica okręgu jest przekątną kwadratu, bo w okręgu kąt oparty na średnicy jest kątem prostym. Stąd średnica kwadratu ma długość $d = 2 r$ . I stąd $P = \frac{d^{2}}{2} = \frac{4 r^{2}}{2} = 2 r^{2}$ .

Przykład 10

Wyznaczymy pole kwadratu opisanego na okręgu o promieniu $r$ .

RVq4d3dRDUq1d

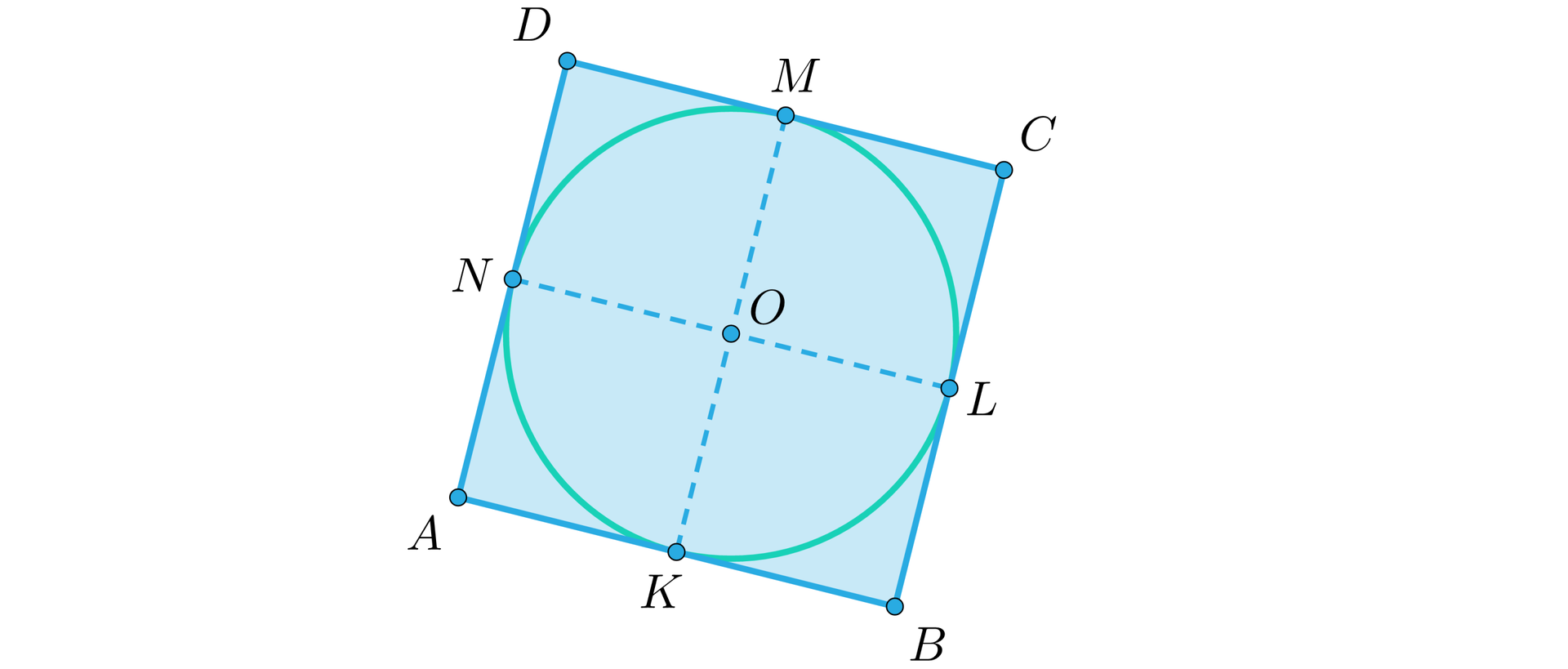
Ilustracja przedstawia kwadrat ABCD opisany na okręgu o promieniu r. Na kwadracie zaznaczono środki boków KLMN połączono je odcinkami przecinającymi się w punkcie O.

Rozwiązanie

Promień okręgu poprowadzony do punktu styczności z kwadratem jest prostopadły do boków kwadratu. Stąd mamy, że kąt $K O N$ jest prosty i odcinki $K O$ i $O N$ są równe. Stąd $A K O N$ jest kwadratem.

To samo zachodzi dla pozostałych wierzchołków kwadratu $A B C D$ , więc średnica okręgu ma długość równą długości boku kwadratu. Stąd $d = 2 r$ i pole $P = {(2 r)}^{2} = 4 r^{2}$ .

Słownik

punkty kratowe

punkty o współrzędnych całkowitych

Wprowadzenie

Symulacja interaktywna

Pole kwadratu o boku długości $n$ , gdzie $n$ jest liczbą naturalną

Pole kwadratu o boku długości $\frac{1}{n}$ , gdzie $n$ jest liczbą naturalną

Pole kwadratu o boku długości wymiernej

Pole kwadratu o boku długości niewymiernej – dla zainteresowanych

Wykorzystanie podobieństwa kwadratów do wyznaczenia pola kwadratu o boku $a$

Wzory skróconego mnożenia

Pole kwadratu, którego wierzchołki mają całkowite współrzędne

Wykorzystanie przekątnej do wyznaczania pola kwadratu

Słownik

Wprowadzenie

Symulacja interaktywna

Przeczytaj

Pole kwadratu o boku długości n, gdzie n jest liczbą naturalną

Pole kwadratu o boku długości 1n, gdzie n jest liczbą naturalną

Pole kwadratu o boku długości wymiernej

Pole kwadratu o boku długości niewymiernej – dla zainteresowanych

Wykorzystanie podobieństwa kwadratów do wyznaczenia pola kwadratu o boku a

Wzory skróconego mnożenia

Pole kwadratu, którego wierzchołki mają całkowite współrzędne

Wykorzystanie przekątnej do wyznaczania pola kwadratu

Słownik

Pole kwadratu o boku długości $n$ , gdzie $n$ jest liczbą naturalną

Pole kwadratu o boku długości $\frac{1}{n}$ , gdzie $n$ jest liczbą naturalną

Wykorzystanie podobieństwa kwadratów do wyznaczenia pola kwadratu o boku $a$