Przeczytaj

Na rysunku poniżej przedstawiono wykresy trzech ciągów.

RDMfYRR3Igeyk

Ilustracja przedstawia interpretację graficzną trzech ciągów: an, bn oraz cn. Na każdym rysunku znajduje się układ współrzędnych z poziomą osią n od zera do sześciu i z pionową osią na każdym rysunku oznaczoną inaczej, kolejno an, bn i cn, każda pionowa oś jest od minus jeden do pięciu. Ciąg an składa się z następujących punktów: 0,1, 1,32, 2,2, 3,52, 4,3, 5,72, 6,4. Ciąg bn składa się z następujących punktów: 0,72, 1,3, 2,52, 3,2, 4,32, 5,1, 6,12. Ciąg cn składa się z następujących punktów: 0,32, 1,32, 2,32, 3,32, 4,32, 5,32, 6,32.

Pierwszy wykres jest wykresem ciągu rosnącego – każdy kolejny wyraz ciągu $(a_{n})$ jest większy od wyrazów poprzednich.

Uwaga

W niektórych przypadkach w tym materiale rozważać będziemy ciągi określone dla wszystkich liczb naturalnych. Najczęściej jednak określamy ciagi tylko dla liczb naturalnych dodatnich. Do takiej dziedziny ograniczymy się więc w definicjach ciągów monotonicznych, choć można analogiczne definicje sformułować dla ciągów określonych w całym zbiorze liczb naturalnych.

Ciąg rosnący

Definicja: Ciąg rosnący

Ciąg $(a_{n})$ nazywamy rosnącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest większy od wyrazu poprzedniego.

Czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} > a_{n}

Drugi wykres – to wykres ciągu malejącegociąg malejącymalejącego – każdy kolejny wyraz ciągu $(b_{n})$ jest mniejszy od wyrazów poprzednich.

Ciąg malejący

Definicja: Ciąg malejący

Ciąg $(a_{n})$ nazywamy malejącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest mniejszy od wyrazu poprzedniego.

Czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} < a_{n}

Trzeci wykres, to wykres ciągu stałego – każdy kolejny wyraz ciągu $(c_{n})$ jest równy wyrazom poprzednim.

Ciąg stały

Definicja: Ciąg stały

Ciąg $(a_{n})$ nazywamy stałym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest równy wyrazowi poprzedniemu.

Czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest równość

a_{n + 1} = a_{n}

Możemy też rozważać ciągi, w których każdy kolejny wyraz ciągu jest nie mniejszy/ nie większy od wyrazu poprzedniego. Taki ciąg nazywamy odpowiednio niemalejącym/ nierosnącym. Ciąg stały jest jednocześnie ciągiem nierosnącym i niemalejącym.

Ciąg niemalejący

Definicja: Ciąg niemalejący

Ciąg $(a_{n})$ nazywamy niemalejącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest równy wyrazowi poprzedniemu lub większy od wyrazu poprzedniego.

Czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} \geq a_{n}

W podobny sposób możemy określić ciąg nierosnący. Wykres takiego ciągu przedstawia poniższy rysunek.

R16F8Wx8ciL44

Ilustracja przedstawia interpretację graficzną ciągu an. Na rysunku znajduje się układ współrzędnych z poziomą osią n od zera do ośmiu oraz z pionową osią an od minus jeden do pięciu. Na płaszczyźnie zaznaczono punkty będące wyrazami ciągu an. Punkty te to: 1,4, 2,4, 3,4, 4,3, 5,3, 6,2, 7,1, 8,1.

Ciąg nierosnący

Definicja: Ciąg nierosnący

Ciąg $(a_{n})$ nazywamy nierosnącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest równy wyrazowi poprzedniemu lub mniejszy od wyrazu poprzedniego.

Czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} \leq a_{n}

O ciągach rosnącychciąg rosnącyrosnących, malejących, stałych, nierosnących, niemalejących (w całej swojej dziedzinie) mówimy, że są to ciągi monotoniczne.

Istnieją też ciągi, które nie mają żadnej z powyższych własności. O takich ciągach mówimy, że nie są monotoniczne. Wykres ciągu, który nie jest monotoniczny przedstawia poniższy rysunek.

RmwQkKQgN2Hl2

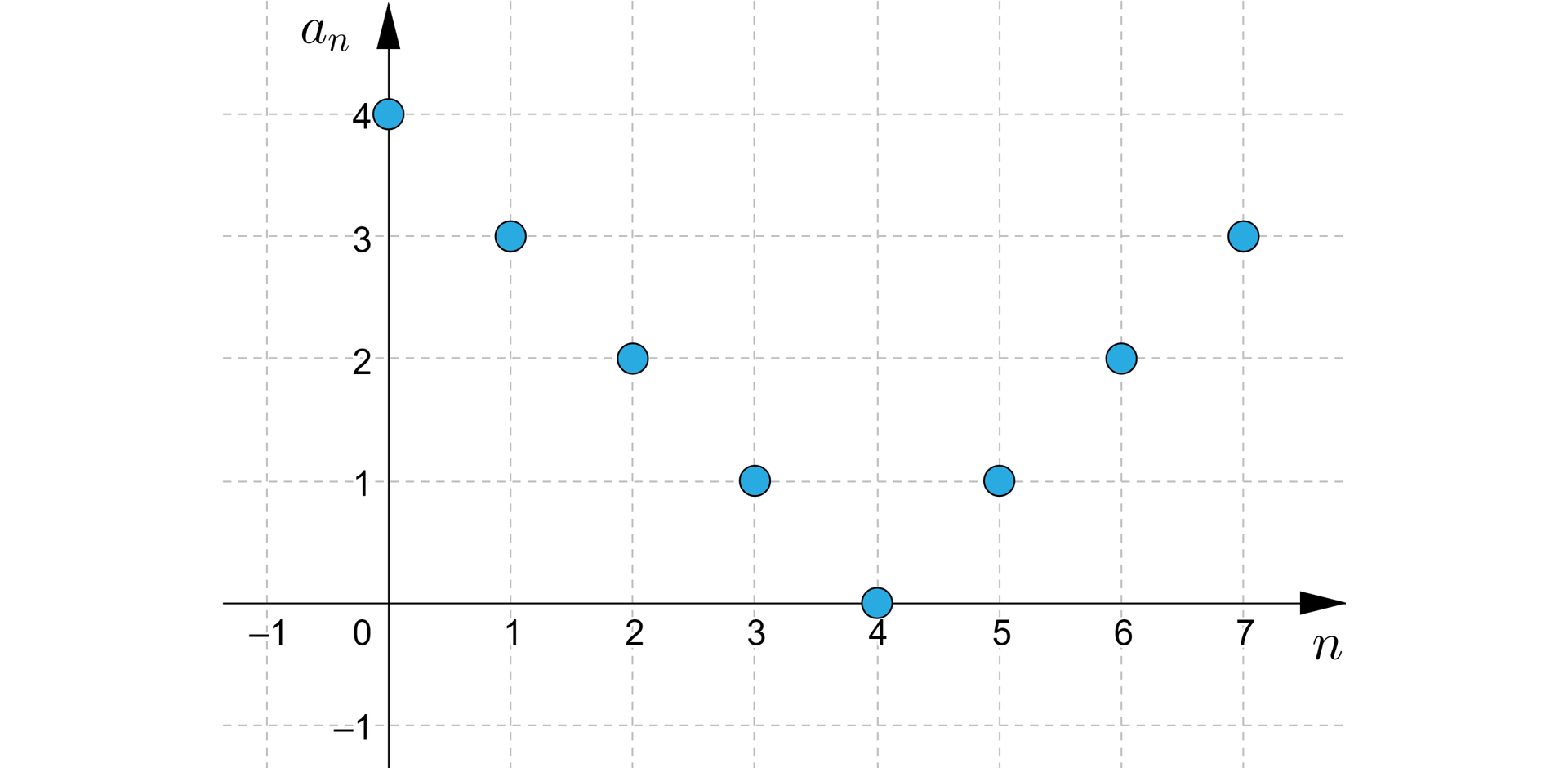
Definicję ciągu rosnącego $(a_{n})$ można zapisać w sposób równoważny w postaci nierówności

a_{n + 1} - a_{n} > 0

która jest spełniona dla każdej liczby naturalnej $n \in ℕ_{+}$ .

Przykład 1

Wykażemy, że ciąg $(a_{n})$ określony dla $n \in ℕ_{+}$ wzorem $a_{n} = \frac{2 n - 1}{n + 3}$ jest rosnący.

Badamy znak różnicy $a_{n + 1} - a_{n}$ .

$a_{n + 1} - a_{n} = \frac{2 (n + 1) - 1}{n + 1 + 3} - \frac{2 n - 1}{n + 3}$

$a_{n + 1} - a_{n} = \frac{2 n + 1}{n + 4} - \frac{2 n - 1}{n + 3}$

Sprowadzamy ułamki do wspólnego mianownika i wykonujemy wskazane działania.

$a_{n + 1} - a_{n} = \frac{(2 n + 1) (n + 3) - (2 n - 1) (n + 4)}{(n + 4) (n + 3)}$

$a_{n + 1} - a_{n} = \frac{2 n^{2} + 7 n + 3 - 2 n^{2} - 7 n + 4}{(n + 4) (n + 3)}$

$a_{n + 1} - a_{n} = \frac{7}{(n + 4) (n + 3)} > 0$

Dla każdej liczby naturalnej $n \in ℕ_{+}$ spełniona jest nierówność $a_{n + 1} - a_{n} > 0$ , zatem ciąg jest rosnący, co należało wykazać.

Przykład 2

Zbadamy monotoniczność ciągu $(b_{n})$ określonego dla $n > 1$ wzorem ogólnym

$b_{n} = \sqrt{n^{2} - n}$ .

Badamy znak różnicy $b_{n + 1} - b_{n}$ .

$b_{n + 1} - b_{n} = \sqrt{{(n + 1)}^{2} - (n + 1)} - \sqrt{n^{2} - n}$

$b_{n + 1} - b_{n} = \sqrt{n^{2} + n} - \sqrt{n^{2} - n}$

Przekształcamy zapisaną różnicę, korzystając ze wzoru skróconego mnożenia na różnicę kwadratów.

$b_{n + 1} - b_{n} = \sqrt{n^{2} + n} - \sqrt{n^{2} - n} \cdot \frac{\sqrt{n^{2} + n} + \sqrt{n^{2} - n}}{\sqrt{n^{2} + n} + \sqrt{n^{2} - n}}$

$b_{n + 1} - b_{n} = \frac{2 n}{\sqrt{n^{2} + n} + \sqrt{n^{2} - n}} > 0$

Dla każdej liczby naturalnej $n > 1$ spełniona jest nierówność $b_{n + 1} - b_{n} > 0$ , zatem ciąg jest rosnący.

Jeśli wszystkie wyrazy ciągu $(a_{n})$ są dodatnie, to ciąg jest rosnący, gdy dla każdej liczby naturalnej $n \in ℕ_{+}$ spełniona jest nierówność

\frac{a_{n + 1}}{a_{n}} > 1

Przykład 3

Zbadamy monotoniczność ciągu $(c_{n})$ określonego dla $n \in ℕ_{+}$ wzorem $c_{n} = {(\frac{3}{2})}^{n}$ .

Badamy znak ilorazu $\frac{c_{n + 1}}{c_{n}}$ .

$\frac{c_{n + 1}}{c_{n}} = {(\frac{3}{2})}^{n + 1} : {(\frac{3}{2})}^{n}$

Przekształcamy otrzymane wyrażenie.

$\frac{c_{n + 1}}{c_{n}} = \frac{3}{2} \cdot {(\frac{3}{2})}^{n} \cdot {(\frac{2}{3})}^{n}$

$\frac{c_{n + 1}}{c_{n}} = \frac{3}{2} > 1$

Dla każdej liczby naturalnej $n \in ℕ_{+}$ spełniona jest nierówność $\frac{c_{n + 1}}{c_{n}} > 1$ , zatem ciąg jest rosnący.

Definicję ciągu malejącego $(a_{n})$ można zapisać w sposób równoważny w postaci nierówności

a_{n + 1} - a_{n} < 0

która jest spełniona dla każdej liczby naturalnej $n \in ℕ_{+}$ .

Przykład 4

Wykażemy, że ciąg $(d_{n})$ określony dla $n \in ℕ_{+}$ wzorem $d_{n} = 6 - 5 n$ jest malejącyciąg malejącymalejący.

Badamy znak różnicy $d_{n + 1} - d_{n}$ .

$d_{n + 1} - d_{n} = 6 - 5 (n + 1) - 6 + 5 n$

$d_{n + 1} - d_{n} = 6 - 5 n - 5 - 6 + 5 n$

$d_{n + 1} - d_{n} < - 5$

Dla każdej liczby naturalnej $n \geq 1$ spełniona jest nierówność $d_{n + 1} - d_{n} < 0$ , zatem ciąg jest malejący, co należało wykazać.

Jeśli wszystkie wyrazy ciągu $(a_{n})$ są dodatnie, to ciąg jest malejący, gdy dla każdej liczby naturalnej $n \in ℕ_{+}$ spełniona jest nierówność

\frac{a_{n + 1}}{a_{n}} < 1

Przykład 5

Zbadamy monotoniczność ciągu $(t_{n})$ określonego dla $n \in ℕ_{+}$ wzorem $t_{n} = {(\frac{1}{2})}^{n}$ .

Badamy znak ilorazu $\frac{t_{n + 1}}{t_{n}}$ .

$\frac{t_{n + 1}}{t_{n}} = \frac{{(\frac{1}{2})}^{n + 1}}{{(\frac{1}{2})}^{n}}$

$\frac{t_{n + 1}}{t_{n}} = \frac{1}{2} < 1$

Wyrazy ciągu są dodatnie i dla każdej liczby naturalnej $n \in ℕ_{+}$ spełniona jest nierówność $\frac{t_{n + 1}}{t_{n}} < 1$ zatem ciąg jest malejący.

W niektórych przypadkach ciąg monotoniczny otrzymujemy dopiero po odrzuceniu pewnej liczby początkowych wyrazów danego ciągu. O takich ciągach mówimy, że są monotoniczne od pewnego miejsca.

Na przykład ciąg $(a_{n})$ , którego wykres przedstawiono na rysunku poniżej, jest rosnącyciąg rosnącyrosnący, począwszy od wyrazu $a_{3}$ .

R1LUilOSr0vE4

Ilustracja przedstawia interpretację graficzną ciągu an. Na rysunku znajduje się układ współrzędnych z poziomą osią n od minus jeden do ośmiu oraz z pionową osią an od minus jeden do pięciu. Na płaszczyźnie zaznaczono punkty będące wyrazami ciągu an. Punkty te to: 0,-213, 1,-314, 2,-334, 3,-4, 4,-334, 5,-313, 6,-213, 7,-34, 8,1.

Przykład 6

Zbadamy monotoniczność ciągu $(a_{n})$ określonego dla $n \geq 1$ wzorem ogólnym $a_{n} = n^{2} - 14 n + 40$ .

Badamy znak różnicy $a_{n + 1} - a_{n}$ .

$a_{n + 1} - a_{n} = {(n + 1)}^{2} - 14 (n + 1) + 40 - n^{2} + 14 n - 40$

$a_{n + 1} - a_{n} = 2 n - 13$

$2 n - 13 > 0$ dla $n > 6, 5$

Począwszy od wyrazu $a_{7}$ ciąg jest rosnący (dla $n \in \{1, 2, 3, 4, 5, 6\}$ ciąg jest malejący).

Słownik

ciąg rosnący

ciąg $(a_{n})$ nazywamy rosnącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest większy od wyrazu poprzedniego; czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} > a_{n}

ciąg malejący

ciąg $(a_{n})$ nazywamy malejącym wtedy i tylko wtedy, gdy każdy wyraz tego ciągu (oprócz wyrazu pierwszego) jest mniejszy od wyrazu poprzedniego; czyli dla każdej liczby $n \in ℕ_{+}$ spełniona jest nierówność

a_{n + 1} < a_{n}

Wprowadzenie

Prezentacja multimedialna

Słownik