Przekrojem osiowym stożka jest trójkąt równoboczny o obwodzie równym $72$. Obliczymy pole powierzchni całkowitej i objętość tego stożka.

Rozwiązanie

Narysujmy stożek wraz z przekrojem osiowym i wprowadźmy oznaczenia, jak na rysunku.

R7o2oaGCvRnD8

Ilustracja przedstawia stożek oraz jego przekrój osiowy będącym trójkątem równoramiennym. Na ilustracji zaznaczono tworzącą stożka l, wysokość h oraz promień podstawy stożka r.

Zauważmy, że $l=2r$ oraz $h=\frac{l\sqrt{3}}{2}$.

Jeżeli obwód trójkąta równobocznego jest równy $72$, zatem $3l=72$, więc $l=24$.

Wobec tego $r=\frac{1}{2}·24=12$ oraz $h=\frac{l\sqrt{3}}{2}=\frac{24\sqrt{3}}{2}=12\sqrt{3}$.

Zatem pole powierzchni całkowitej stożka jest równe:

$P_c=\pi ·{12}^2+\pi ·12·24=144\pi +288\pi =432\pi$.

Objętość stożka wynosi:

$V=\frac{1}{3}\pi ·{12}^2·12\sqrt{3}=576\sqrt{3}\pi$.

Tworząca stożka ma długość $16$, a przekrojem poprzecznym stożka jest koło o polu równym $20\pi$. Wiadomo, że płaszczyzna przekroju podzieliła wysokość stożka w stosunku $2:1$, jak na rysunku. Obliczymy objętości brył, na jakie płaszczyzna przekroju podzieliła ten stożek.

R9wiYZVv6xuRZ

Ilustracja przedstawia stożek o promieniu podstawy R oraz jego przekrój poprzeczny będącym kołem o promieniu r. Przekrój ten jest równoległy do podstawy stożka i jest od niego oddalony o dwa h. Sumaryczna wysokość stożka ma długość trzy h, natomiast tworząca stożka ma długość l.

Rozwiązanie

Z treści zadania mamy $l=16$.

Ponieważ pole przekroju jest równe $20\pi$, zatem:

$\pi ·r^2=20\pi$

$r^2=20$, czyli $r=2\sqrt{5}$.

Jeżeli płaszczyzna przekroju podzieliła wysokość stożka w stosunku $2:1$, to:

$R=3·r=3·2\sqrt{5}=6\sqrt{5}$.

Długość wysokości mniejszego stożka obliczymy, korzystając z twierdzenia Pitagorasa:

${\left(3h\right)}^2+R^2=l^2$

$9h^2+{\left(6\sqrt{5}\right)}^2={16}^2$

$9h^2+180=256$

$9h^2=76$

$h^2=\frac{76}{9}$, czyli $h=\frac{2\sqrt{19}}{3}$.

Zatem objętość całego stożka wynosi:

$V=\frac{1}{3}·\pi ·R^2·3h=\frac{1}{3}·\pi ·{\left(6\sqrt{5}\right)}^2·2\sqrt{19}=120\sqrt{19}\pi$.

Niech $V_1$ będzie objętością stożka o podstawie $r$ i wysokości $h$. Wówczas:

$V_1=\frac{1}{3}·\pi ·r^2·h=\frac{1}{3}·\mathrm{\pi }·{\left(2\sqrt{5}\right)}^2·\frac{2\sqrt{19}}{3}=\frac{40\sqrt{19}}{9}\mathrm{\pi }$.

Niech $V_2$ będzie objętością drugiej bryły powstałej po przecięciu stożka podaną płaszczyzną. Wówczas:

$V_2=V-V_1=120\sqrt{19}\pi -\frac{40\sqrt{19}}{9}\pi =\frac{1040\sqrt{19}}{9}\mathrm{\pi }$.

Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu $12$. Obliczymy pole przekroju osiowego tego stożka.

Rozwiązanie

Narysujmy wycinek koła o promieniu $12$.

R9mqcqPEZfrRg

Ilustracja przedstawia wycinek koła o promieniu dwanaście. Kąt zawarty pomiędzy dwoma promieniami wynosi dziewięćdziesiąt stopni.

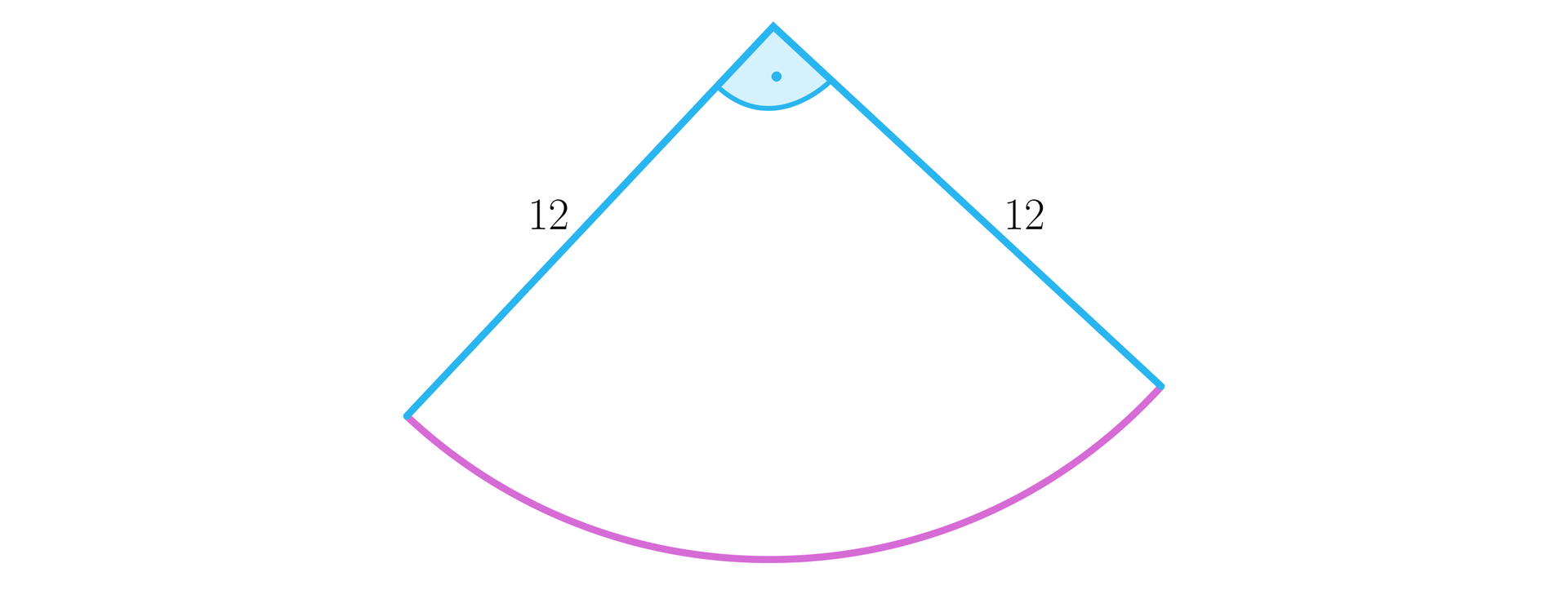
Pole tego wycinka jest równe:

$P=\frac{1}{2}\pi ·{12}^2=72\pi$.

Pole tego wycinka jest równe polu powierzchni bocznej stożka, zatem:

$72\pi =\pi ·r·12$, czyli $r=6$.

Przekrojem osiowym stożka jest trójkąt równoramienny o wymiarach, jak na rysunku.

R16BaRkv1wGGT

Ilustracja przedstawia trójkąt równoramienny. Połowa podstawy trójkąta ma długość sześć, natomiast długość jego ramienia wynosi dwanaście. Z górnego wierzchołka figury upuszczono wysokość h padającą na środek podstawy.

Wysokość tego trójkąta obliczymy, korzystając z twierdzenia Pitagorasa:

$h^2+6^2={12}^2$

$h^2+36=144$

$h^2=108$

$h=6\sqrt{3}$.

Zatem pole tego przekroju jest równe:

$P=\frac{1}{2}·12·6\sqrt{3}=36\sqrt{3}$.

Przez wierzchołek stożka o promieniu podstawy $16$ i wysokości $8$ poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy stożka pod kątem $30°$. Obliczymy pole przekroju tego stożka.

Rozwiązanie

Narysujmy stożek oraz opisany przekrój.

R1Cez6nEUqZ0Q

Ilustracja przedstawia stożek oraz jego przekrój osiowy będącym trójkątem równoramiennym. Na ilustracji zaznaczono wysokość stożka o długości osiem. W trójkącie równoramiennym na środek cięciwy podstawy stożka upuszczono wysokość oznaczoną jako h. Punkt upuszczenia wysokości połączono ze środkiem podstawy stożka. Odcinek ten ma długość x. Koniec cięciwy został połączony ze środkiem podstawy stożka tworząc odcinek o długości szesnaście, a sama cięciwa ma długość dwa y. Na płaszczyźnie podstawy stożka powstał trójkąt prostokątny o przyprostokątnych x i y oraz przeciwprostokątnej równej szesnaście.

Ponieważ $\sin 30°=\frac{1}{2}$, zatem:

$\frac{8}{h}=\frac{1}{2}$

Czyli $h=16$.

Wobec tego $x=8\sqrt{3}$.

Długość odcinka $y$ obliczamy z twierdzenia Pitagorasa:

$y^2+x^2=r^2$

$y^2+{\left(8\sqrt{3}\right)}^2={16}^2$

$y^2+192=256$

$y^2=64$

$y=8$.

Długość podstawy trójkąta, który jest przekrojem tego stożka, wynosi $16$.

Zatem pole tego przekroju jest równe:

$P=\frac{1}{2}·16·16=128$.

Przekrojem osiowym stożka jest trójkąt równoramienny o kącie przy wierzchołku, którego cosinus jest równy $\frac{1}{3}$. Wyznaczymy objętość stożka jeżeli wiadomo, że tworząca stożka ma długość $3$.

Rozwiązanie

Przekrojem osiowym stożka jest trójkąt równoramienny o bokach $l$, $l$, $2r$ oraz kącie przy wierzchołku $\alpha$, przy czym $\cos \alpha =\frac{1}{3}$.

R1Q5KUjJRwKTD

Ilustracja przedstawia stożek oraz jego przekrój osiowy będącym trójkątem równoramiennym. Na ilustracji zaznaczono tworzącą stożka l, wysokość h oraz promień podstawy stożka r. Kąt pomiędzy dwoma ramionami trójkąta został oznaczony jako alfa.

Zatem do wyznaczenia wartości $r$ wykorzystamy twierdzenie cosinusów i rozwiązujemy równanie:

${\left(2r\right)}^2=l^2+l^2-2·l·l·\cos \alpha$

$4r^2=3^2+3^2-2·3·3·\frac{1}{3}$

$4r^2=12$

$r^2=3$, czyli $r=\sqrt{3}$.

Wysokość $h$ trójkąta równoramiennego obliczymy z twierdzenia Pitagorasa. Zatem:

$h^2+{\left(\sqrt{3}\right)}^2=3^2$

$h^2+3=9$

$h^2=6$

$h=\sqrt{6}$.

Wobec tego objętość stożka jest równa:

$V=\frac{1}{3}·\pi ·{\left(\sqrt{3}\right)}^2·\sqrt{6}=\frac{1}{3}·3\sqrt{6}\pi =\sqrt{6}\pi$.

bryła obrotowa, która powstaje przez obrót trójkąta prostokątnego wokół osi zawierającej jedną z przyprostokątnych

kąt pomiędzy ramionami trójkąta, będącego przekrojem osiowym stożka