Przeczytaj
Symetralna odcinka
Symetralną odcinka nazywamy prostą prostopadłą do tego odcinka i przechodzącą przez jego środek.
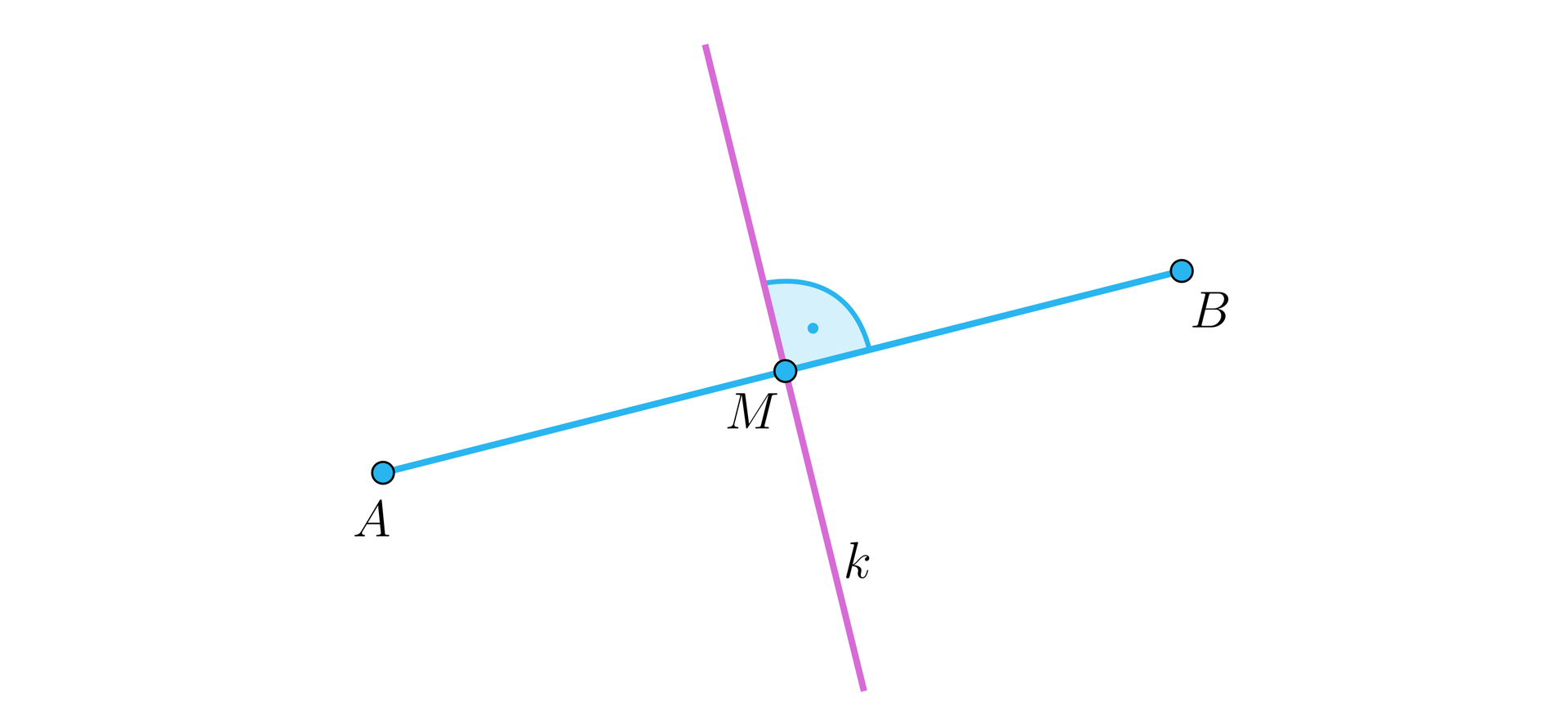
Geometryczna własność symetralnej odcinka
Podamy teraz ważną własność symetralnej odcinka.
Jeżeli punkt leży na symetralnej odcinka , to .
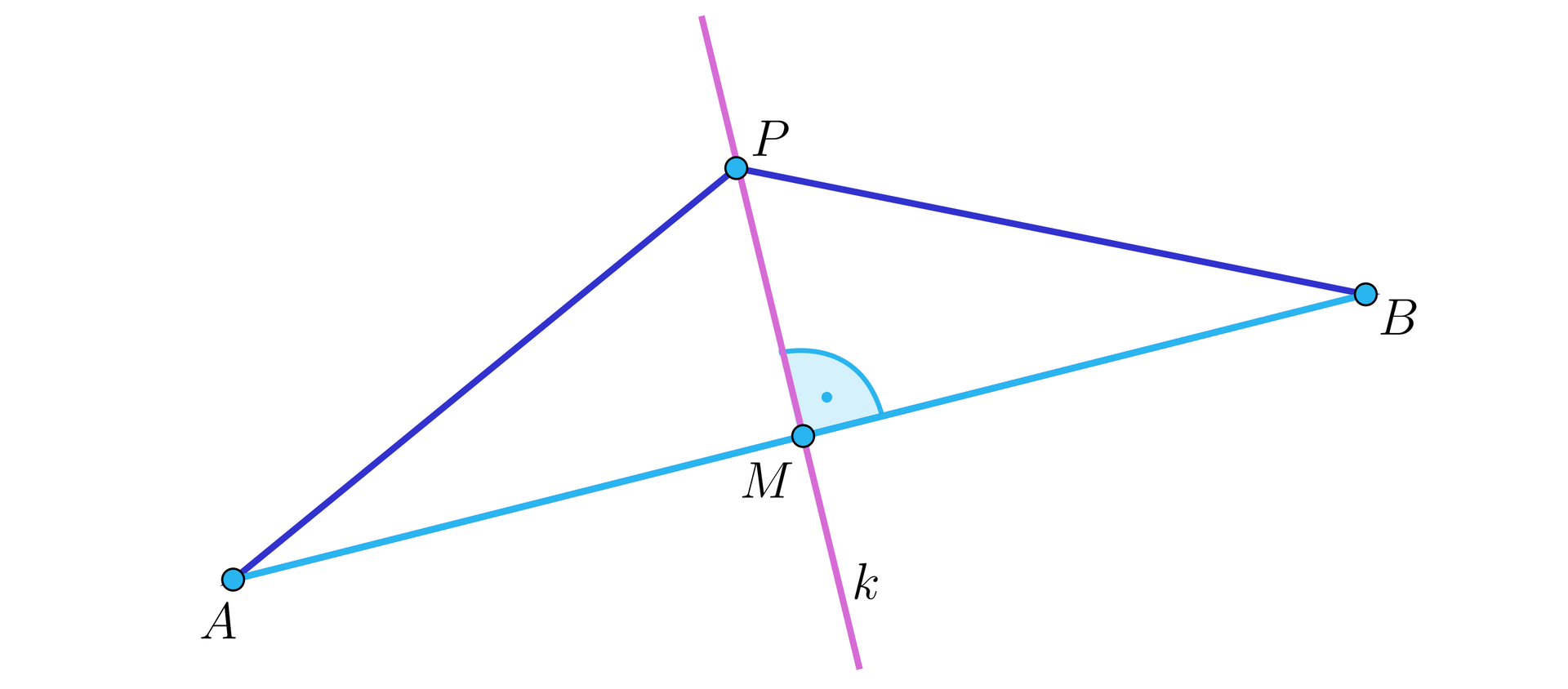
Załóżmy, że jest dowolnym punktem leżącym na symetralnej odcinka . Jeśli jest środkiem odcinka , to oczywiście . Jeśli natomiast nie jest środkiem odcinka , to wtedy trójkąty i , gdzie oznacza środek odcinka , są przystające. Wynika to z cechy przystawania trójkątów (odcinek jest wspólnym bokiem tych trójkątów, kąty i są proste oraz ). To kończy dowód.
Jeżeli jest takim punktem płaszczyzny, że , to leży na symetralnej odcinka .
Załóżmy, że jest takim punktem płaszczyzny, że . Jeśli jest środkiem odcinka , to z definicji symetralnej odcinka wynika, że leży on na symetralnej odcinka .

Jeśli nie jest środkiem odcinka , to wtedy trójkąty i , gdzie oznacza środek odcinka , są przystające. Wynika to z cechy przystawania trójkątów (odcinek jest wspólnym bokiem tych trójkątów, , co wynika z założenia, oraz ). Stąd wynika, że kąty i są równe, ale suma tych kątów jest kątem półpełnym, więc każdy z tych kątów jest prosty. To z kolei oznacza, że prosta jest prostopadła do odcinka i przechodzi przez środek tego odcinka, a więc jest to symetralna odcinka . To kończy dowód.
Te dwa twierdzenia często zapisujemy w postaci jednego twierdzenia.
Symetralna odcinka jest zbiorem wszystkich punktów płaszczyzny równo oddalonych od jego końców.
Konstrukcja symetralnej odcinka
Ponieważ symetralna jest prostą, więc wystarczy znaleźć dwa różne punkty przez które ta symetralna przechodzi. Z własności symetralnej wynika, że każdy z tych punktów musi być równo oddalony od końców odcinka. Wystarczy w tym celu narysować dwa przecinające się okręgi o tych samych promieniach i środkach będących końcami odcinka. Kolejne etapy konstrukcji symetralnej odcinka pokazuje animacja.


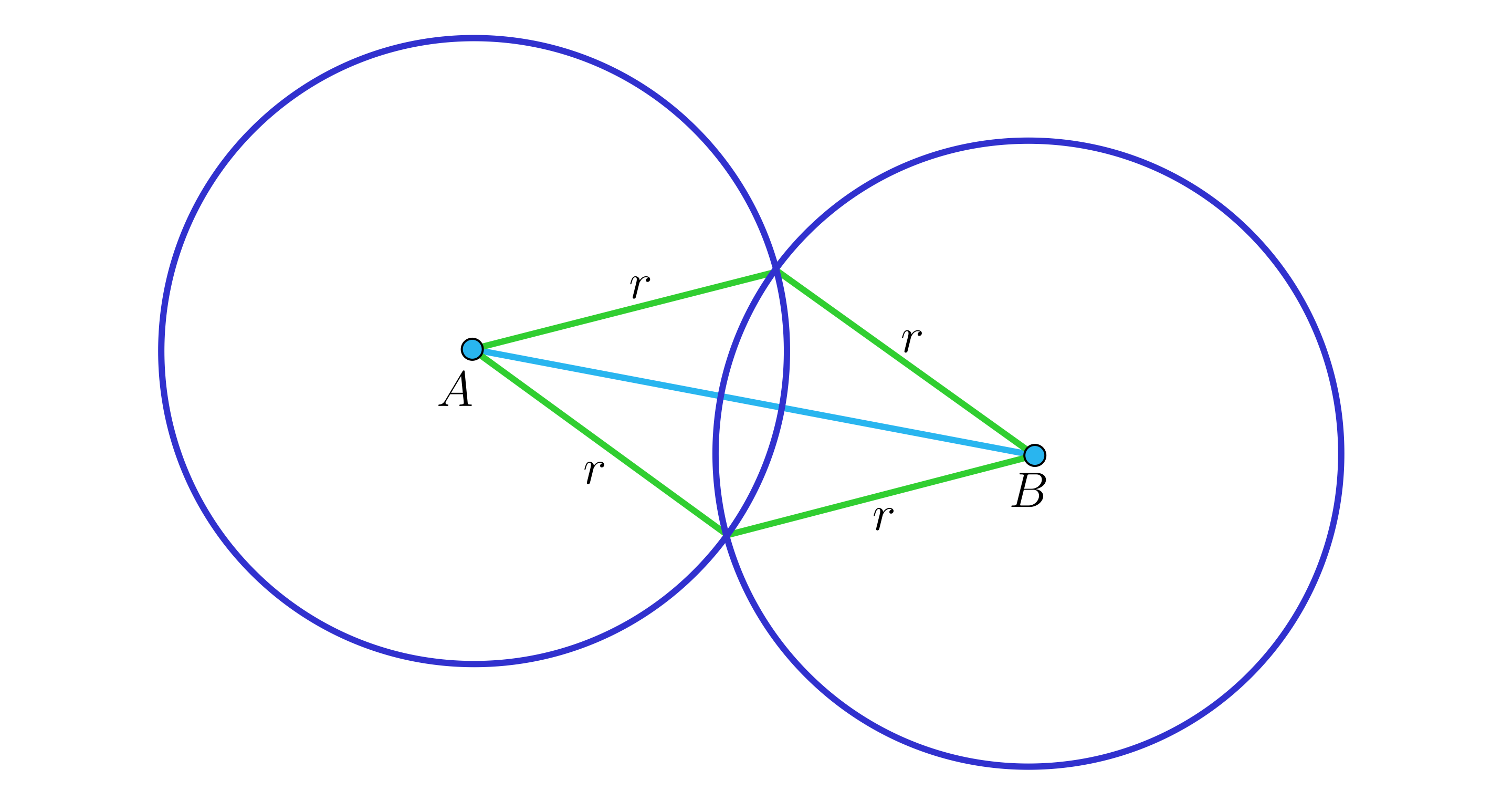



Animacja przedstawia kolejne kroki prowadzące do otrzymania symetralnej odcinka. Najpierw rysujemy odcinek A B. Następnie, biorąc punk A jako środek okręgu, rysujemy okrąg o promieniu r, przy czym promień musi być mniejszy od długości odcinka A B i większy od połowy jego długości. Rysujemy drugi okrąg o takim samym promieniu, ale o środku w punkcie B. Okręgi przecinają się. Zaznaczamy miejsca przecięcia okręgów jako punkty na przykład P i Q. Prowadzimy prostą k przez punkty przecięcia okręgów. Prosta k jest symetralną odcinka A B.
Poprawność tej konstrukcji wynika wprost z faktu, że końce odcinka oraz punkty i przecięcia okręgów są wierzchołkami rombu o boku długości , a przekątne rombu są prostopadłe i wzajemnie się połowią, więc prosta jest prostopadła do odcinka , a punkt jej przecięcia z tym odcinkiem jest jego środkiem.
W praktyce, konstruując symetralną odcinka, nie rysujemy całych okręgów, a jedynie takie łuki tych okręgów, które przecinają się w dwóch punktach.
Konstruując symetralną odcinka, konstruujemy też środek tego odcinka.
Prześledźmy kilka przykładów, w których wykorzystamy symetralną.
Podziel konstrukcyjnie dany odcinek na cztery równe części.
W pierwszym kroku skonstruujemy symetralną odcinka . Punkt jej przecięcia z odcinkiem jest środkiem tego odcinka. Powtarzamy konstrukcję symetralnej dla każdego z odcinków i . Punkty i przecięcia tych symetralnych i odcinków odpowiednio i wraz z punktem to szukane punkty podziału.

Na płaszczyźnie dane są trzy punkty: , , . Udowodnij, że jeśli symetralne odcinków i są równoległe, to , i są punktami współliniowymipunktami współliniowymi.
Niech i oznaczają symetralne odcinków odpowiednio i .

Z definicji symetralnej odcinka wynika, że i . Stąd i z założenia, że wynika, że . To z kolei oznacza, że punkty , i są współliniowe. To kończy dowód.
W ostatnim przykładzie pokażemy rozwiązanie problemu wyboru właściwego miejsca na wybudowanie przejazdu nad (lub pod) autostradą.
W pobliżu dwóch miejscowości A i B będzie przechodziła autostrada tak, że te miejscowości będą rozdzielone tą autostradą.
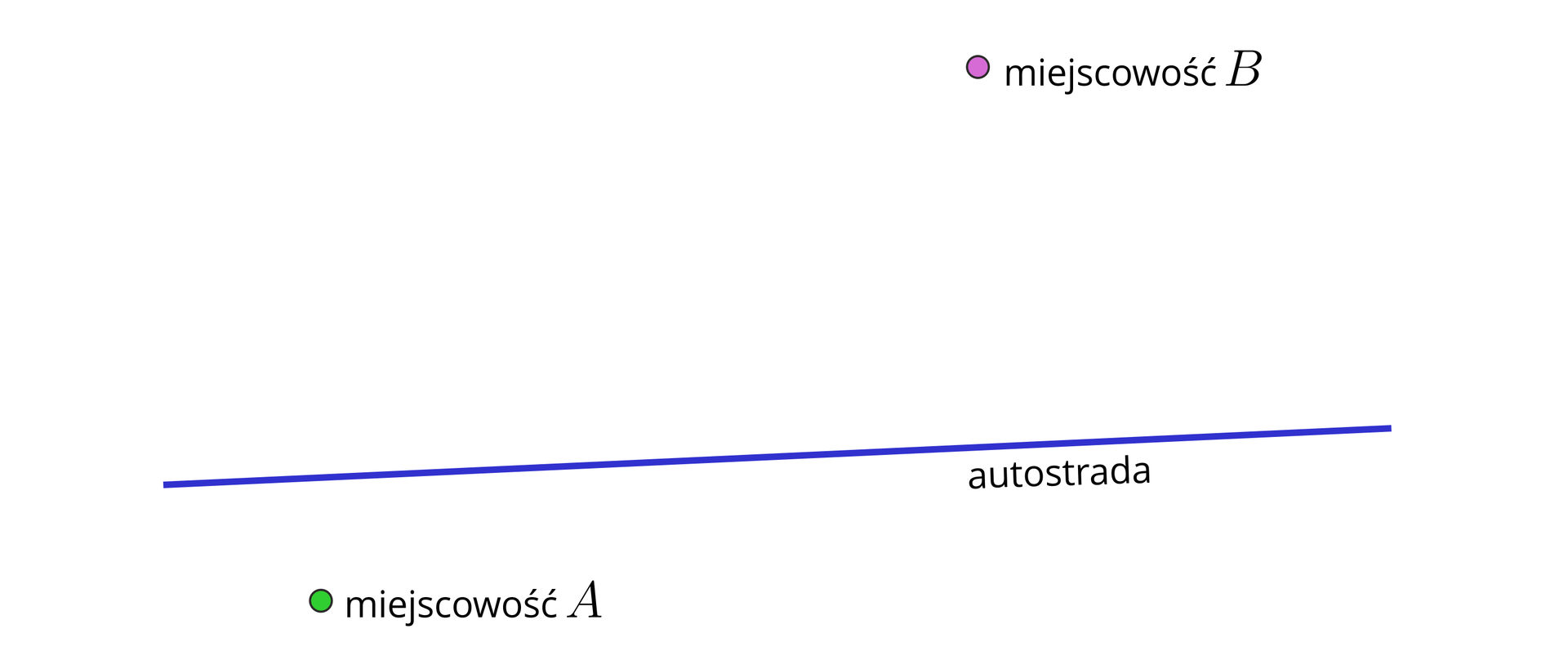
Musimy znaleźć na „autostradzie” taki punkt , żeby zachodziła równość . W tym celu narysujmy odcinek , a następnie skonstruujmy jego symetralną . Punkt jej przecięcia z „autostradą” jest szukanym przez nas punktem .

Istotnie spełnia on oba warunki, a więc leży na „autostradzie” oraz jest równo oddalony od punktów i , gdyż leży na symetralnej odcinka .
Słownik
punkty, które leżą na jednej prostej; w przypadku trzech parami różnych punktów możemy zapisać: punkty , , są współliniowe wtedy i tylko wtedy, gdy lub lub