Ciągiem nieskończonym nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich.

Ciągiem skończonym nazywamy funkcję, której dziedziną jest zbiór $n$ liczb naturalnych $\left\{1, 2, 3, ..., n\right\}$.

$\left(-8, 4, 0, 9, -11\right)$ – ciąg pięciowyrazowy skończony, którego kolejnymi wyrazami są liczby: $-8, 4, 0, 9, -11$,

$0, 2, 4, 6, 8, ...$ – nieskończony ciąg, którego wyrazami są kolejne liczby naturalne parzyste,

$\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, ...$ – nieskończony ciąg, którego wyrazami są odwrotności kolejnych liczb naturalnych dodatnich.

Obliczymy pięć początkowych wyrazów ciągu $\left(a_n\right)$ o wzorze ogólnym
$a_n=\sqrt{n+1}$.

Do wzoru postawiamy kolejne liczby naturalne.

$a_1=\sqrt{1+1}=\sqrt{2}$,

$a_2=\sqrt{2+1}=\sqrt{3}$,

$a_3=\sqrt{3+1}=\sqrt{4}=2$,

$a_4=\sqrt{4+1}=\sqrt{5}$,

$a_5=\sqrt{5+1}=\sqrt{6}$.

Ciąg $\left(a_n\right)$ określony jest wzorem ogólnym $a_n=2^n+n^2$.

Znajdziemy wszystkie takie wyrazy ciągu $a_k$, że $k$ jest liczbą pierwszą i $2^k+k^2$ jest też liczbą pierwszą.

Liczba $2^k+k^2$ jest liczbą większą od $2$. Jako liczba pierwsza jest więc liczbą nieparzystą.

Zatem $k$ jest liczbą nieparzystą.

Wówczas $2^k$ w dzieleniu przez $3$ daje resztę $2$.

Natomiast $k^2$ w dzieleniu przez $3$ daje resztę $0$ lub $1$.

Aby suma $2^k+k^2$ nie była podzielna przez $3$, to $k$ musi być liczbą podzielną przez $3$.

Ponieważ $k$ jest liczbą pierwszą, zatem $k=3$.

Wtedy $2^3+3^2=17$.

Odpowiedź:

W ciągu $\left(a_n\right)$ istnieje tylko jeden wyraz o szukanej własności, jest to wyraz $a_3$.

Ciąg $\left(a_n\right)$ określony jest wzorem ogólnym: $a_n=n$. Znajdziemy w tym  ciągu  cztery kolejne wyrazy, których iloczyn powiększony o $4^5$ jest kwadratem liczby naturalnej. Zauważmy, że kolejne wyrazy ciągu różnią się o $1$.

Oznaczmy:
$a$, $a+1$, $a+2$, $a+3$ – kolejne wyrazy ciągu,
$x$ – liczba będąca kwadratem liczby naturalnej.

Na podstawie treści zadania zapisujemy równanie, którego rozwiązania będziemy poszukiwać.

$a\left(a+1\right)\left(a+2\right)\left(a+3\right)+4^5=x^2$

Przekształcamy otrzymane równanie.

$a\left(a+1\right)\left(a+2\right)\left(a+3\right)+1024=x^2$

$a(a+1)(a+2)(a+3)=x^2-1024$

$a^4+6a^3+11a^2+6a=x^2-1024$

${\left(a^2+3a+1\right)}^2-1=x^2-1024$

Oznaczmy:
$a^2+3a+1=y$.

$y^2-1=x^2-1024$

Rozwiązujemy równanie

$x^2-y^2=1023$

Ponieważ $1023=3\cdot 11\cdot 31$, stąd

$x^2-y^2=3\cdot 11\cdot 31$

$(x-y)(x+y)=3\cdot 11\cdot 31$

Prawa strona zapisanej równości jest dodatnia, zatem lewa też musi być dodatnia.

Zatem

$\left(x-y\right)\left(x+y\right)=1·1023\Rightarrow y=511$

lub

$\left(x-y\right)\left(x+y\right)=3·341\Rightarrow y=169$

lub

$\left(x-y\right)\left(x+y\right)=11·93\Rightarrow y=41$

lub

$\left(x-y\right)\left(x+y\right)=31·33\Rightarrow y=1$

Jedynie $y=41$ jest wartością trójmianu $a^2+3a+1$ dla liczby naturalnej, $a=5$.

Zatem

$5·6·7·8+1024={52}^2$

Odpowiedź:

Kolejne szukane wyrazy ciągu to $a_5$, $a_6$, $a_7$, $a_8$.

• Ciągiem skończonymciąg skończonyCiągiem skończonym jest lista lekcji, które odbywają się w środy w klasie $\text{IIc}$.

  Kolejnym liczbom naturalnym przyporządkowane są nazwy odpowiednich przedmiotów szkolnych.

  $1\to$ geografia

  $2\to$ j. polski

  $3\to$ matematyka

  $4\to$ historia

  $5\to$ fizyka

• Każdej liczbie naturalnej mniejszej od $6$ przyporządkowujemy sumę cyfr iloczynu tej liczby i liczby $104$.

  Wyrazy tego ciągu:

  $a_1=1+4=5$

  $a_2=2+8=10$

  $a_3=3+1+2=6$

  $a_4=4+1+6=11$

  $a_5=5+2=7$

• Ciąg $\left(d_n\right)$ określony jest następująco: $d_n$ oznacza liczbę dzielników naturalnych liczby naturalnej dodatniej $n$.

  Kilka początkowych wyrazów ciągu:

  $d_1=1$

  $d_2=2$

  $d_3=2$

  $d_4=3$

  $d_5=2$

Rysunek przedstawia wykres ciągu $a_n=\sqrt{n}-2$ dla $1\le n\le 9$ i $n\in \mathrm{\mathbb{N}}$.

R15vKipddRCks

Ilustracja przedstawia układ współrzędnych z poziomą osią n od minus jeden do dziewięciu oraz z pionową osią $a_n$ od minus dwóch do trzech. Na płaszczyźnie zaznaczono następujące 9 punktów: $\left(1;-1\right), \left(2;-\frac{1}{2}\right), \left(3;-\frac{1}{4}\right), \left(4;0\right), \left(5;\frac{1}{4}\right), \left(6;\frac{1}{2}\right), \left(7;\frac{3}{4}\right), \left(8;\frac{7}{8}\right), \left(9;1\right)$.

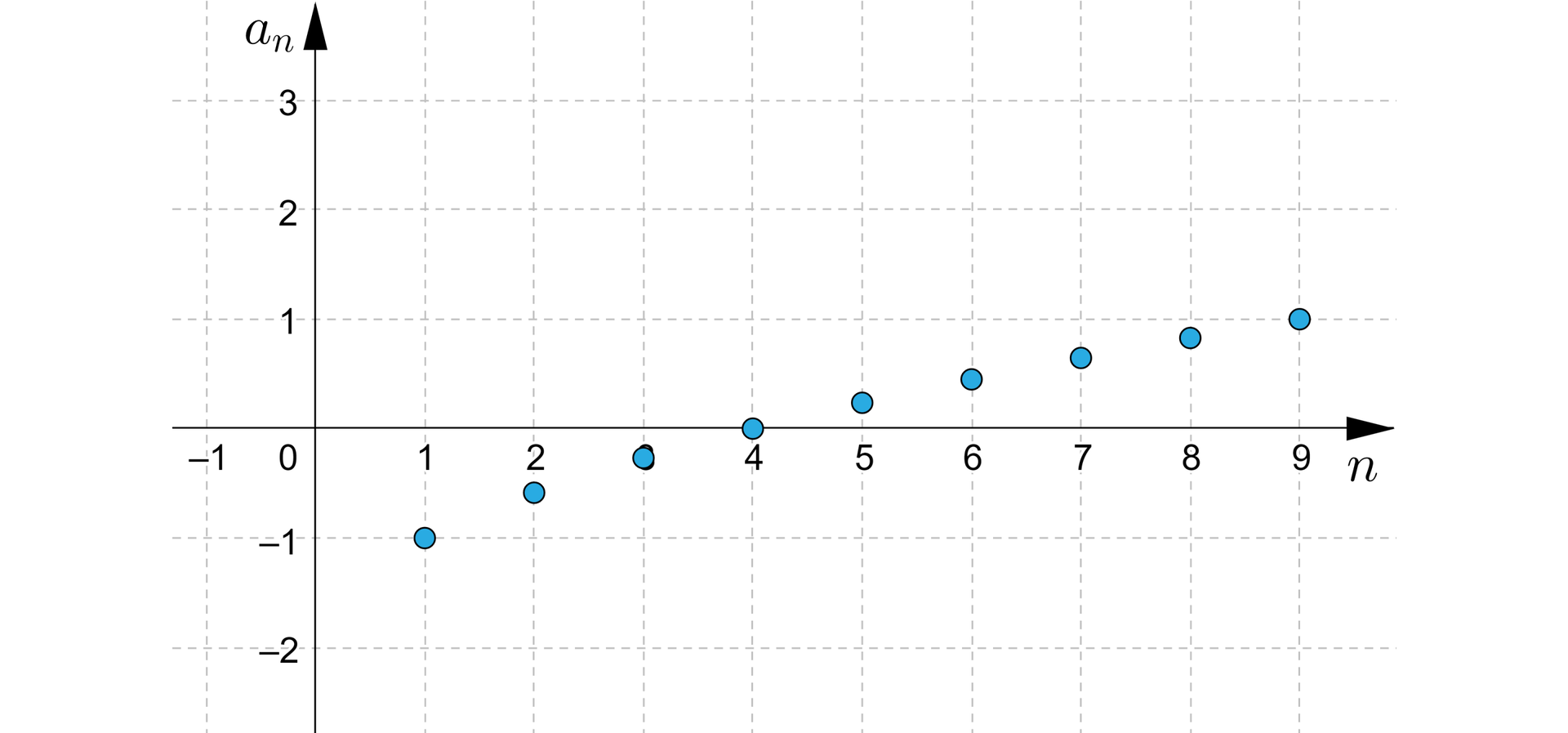
Z wykresu możemy odczytać na przykład, że:

$a_1=-1$,

$a_4=0$,

$a_9=1$.

Sporządzimy wykres ciągu $\left(a_n\right)$ określonego wzorem $a_n=-n+4$ dla $n\in \left\{1, 2, \mathrm{3,} 4, \mathrm{5,} 6\right\}$.

Wyznaczamy kolejne wyrazy ciągu.

$a_1=-1+4=3$

$a_2=-2+4=2$

$a_3=-3+4=1$

$a_4=-4+4=0$

$a_5=-5+4=-1$

$a_6=-6+4=-2$

Wykresem ciągu jest zbiór punktów $\left(n, a_n\right)=\left(n, -n+4\right)$. Zaznaczamy te punkty w układzie współrzędnych.

R1Tsa6aPEEoAx

Ilustracja przedstawia układ współrzędnych z poziomą osią n od minus jeden do siedmiu oraz z pionową osią $a_n$ od minus dwóch do trzech. Na płaszczyźnie zaznaczono następujące 6 punktów: $\left(1;3\right), \left(2;2\right), \left(3;1\right), \left(4;0\right), \left(5;-1\right), \left(6;-2\right)$.

Ciąg $\left(a_n\right)$, przedstawiony na rysunku powyżej, można opisać za pomocą zbioru uporządkowanych par

$\left\{\left(1, 3\right), \left(2, 2\right), \left(3, 1\right), \left(4, 0\right), \left(5, -1\right), \left(6, -2\right)\right\}$.

ciągiem nieskończonym nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich

ciągiem skończonym nazywamy funkcję, której dziedziną jest zbiór $n$ liczb naturalnych $\left\{1, 2, 3, ..., n\right\}$