Objętość graniastosłupa prawidłowego czworokątnego jest równa iloczynowi pola podstawy przez wysokość

RTEMX5DZ7fc7Z

Ilustracja przedstawia graniastosłup prawidłowy czworokątny. Krawędzie podstawy są równe a, a wysokość równa h.

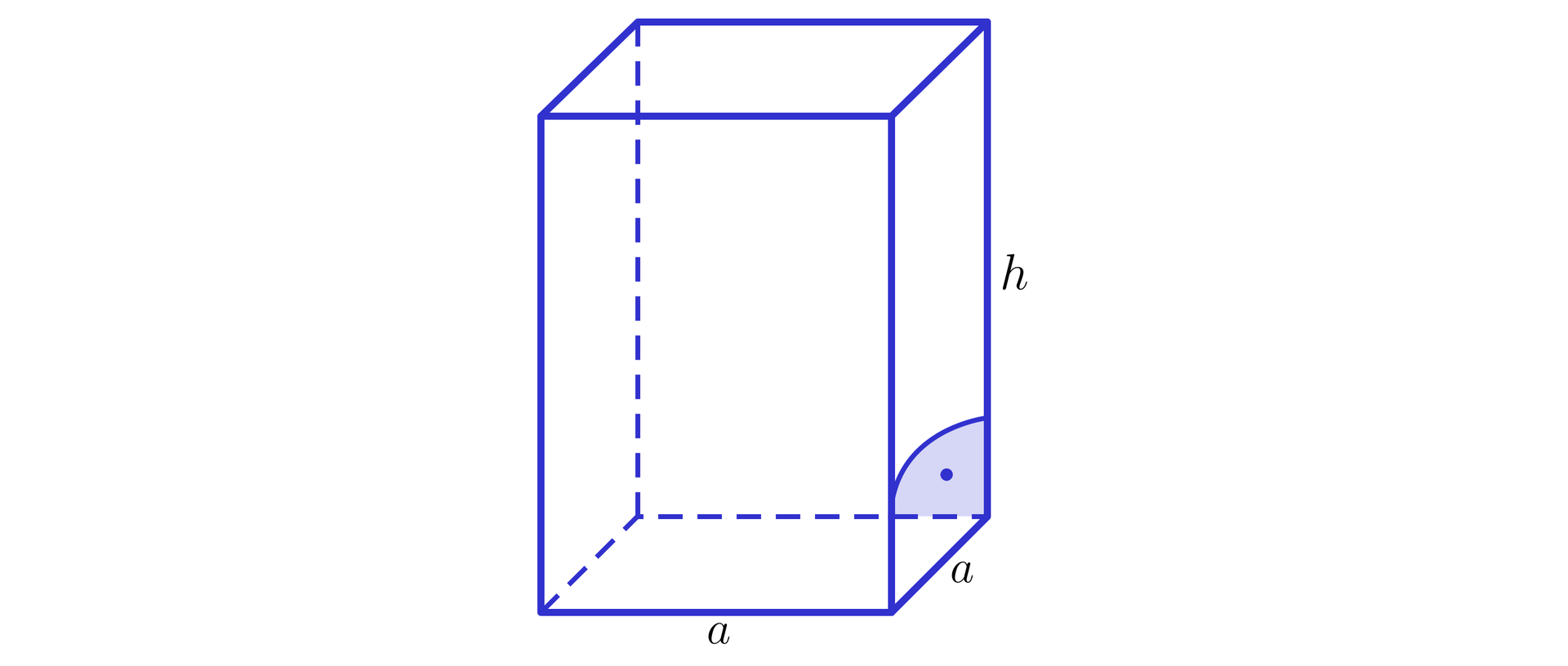
Objętość sześcianusześciansześcianu o krawędzi $a$ wyraża się za pomocą wzoru:

W graniastosłupie prawidłowym czworokątnymgraniastosłup prawidłowy czworokątnygraniastosłupie prawidłowym czworokątnym krawędź podstawy jest równa $a$, zaś przekątna tworzy ze ścianą boczną kąt $\alpha$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie

R1qMr5v53IebC

Ilustracja przedstawia graniastosłup prawidłowy czworokątny A B C D E F G H. Krawędzie podstawy są równe a, a wysokość równa h. Z punktu A i B poprowadzono dwie przekątne graniastosłupa do punktu G. Kąt przy wierzchołku G ma miarę $\alpha$.

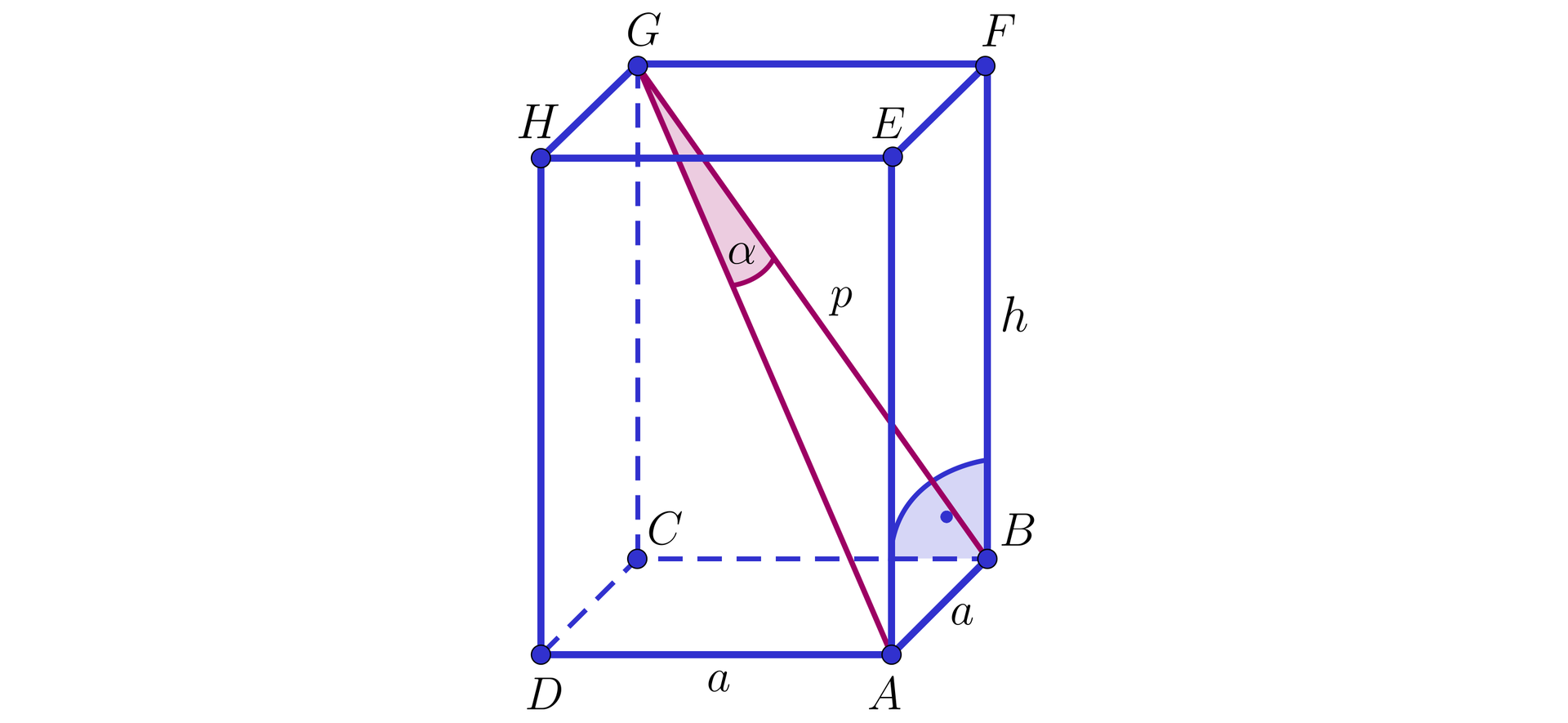
Niech $h$ oznacza długość wysokości rozważanego graniastosłupa, $p$ będzie długością przekątnej ściany bocznej. Wówczas trójkąt $ABG$ jest prostokątny. Stosując twierdzenie Pitagorasatwierdzenie Pitagorasatwierdzenie Pitagorasa, otrzymujemy: $h^2=p^2-a^2$. Następnie z trójkąta $GBA$ mamy $p=\frac{a}{\mathrm{tg}\alpha }$,

więc $h^2=a^2\left(\frac{1}{{\mathrm{tg}}^2\alpha }-1\right)=\frac{a^2\left({\cos }^2\alpha -{\sin }^2\alpha \right)}{{\sin }^2\alpha }=\frac{a^2·\cos 2\alpha }{{\sin }^2\alpha }$.

Możemy już obliczyć objętość naszego graniastosłupa:

$V=a^{2}h=\frac{a^3\sqrt{\cos 2\alpha }}{\sin \alpha }$, $0<\alpha <45°$.

W graniastosłupie prawidłowym czworokątnym pole podstawy jest równe $P$, a pole ściany bocznej $S$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie

Niech $a$ oznacza długość krawędzi, $h$ długość wysokości rozważanego graniastosłupa. Zatem $a=\sqrt{P}$ oraz $S=ah=\sqrt{P}h$, stąd $h=\frac{S}{\sqrt{P}}$. Możemy obliczyć objętość naszego graniastosłupa

$V=a^{2}h=P·\frac{S}{\sqrt{P}}=S\sqrt{P}$.

Graniastosłup prawidłowy czworokątny o krawędzi podstawy długości $a$, przecięto płaszczyzną tak jak pokazano na rysunku.

R1T8nKKV10Fe0

Ilustracja przedstawia graniastosłup prawidłowy czworokątny. Przecięto go płaszczyzną w kształcie rombu o kącie ostrym, nachyloną do podstawy graniastosłupa. Odcinek łączący punkt przecięcia przekątnych rombu i punkt przecięcia przekątnych podstawy graniastosłupa jest prostopadły do podstawy graniastosłupa.

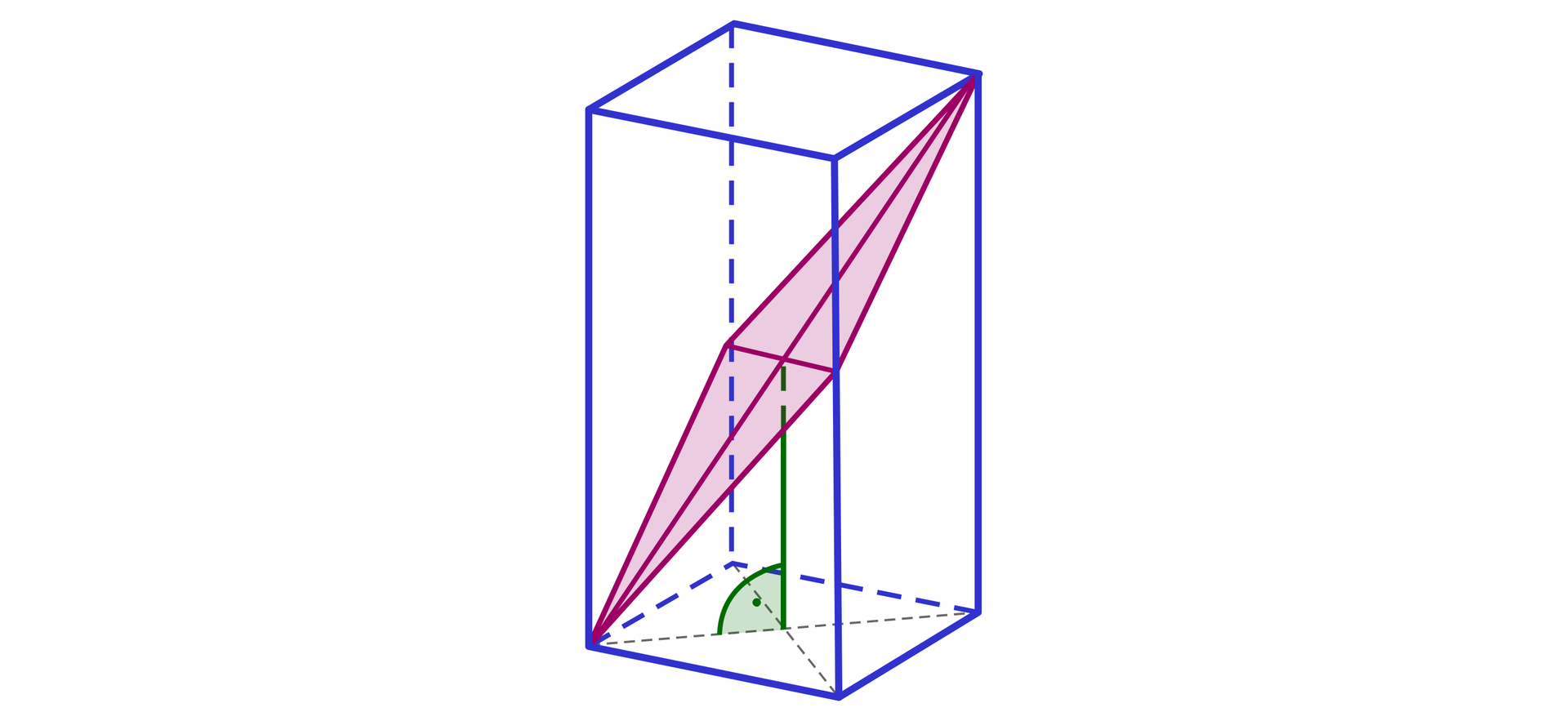
Przekrojem jest romb o kącie ostrym, którego tangens jest równy $\sqrt{3}$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie:

RWCUIEjySPfgT

Ilustracja przedstawia graniastosłup prawidłowy czworokątny A B C D E F G H, krawędzie podstawy mają długość a, a wysokość długość h. Przecięto go płaszczyzną w kształcie rombu o kącie ostrym, nachyloną do podstawy graniastosłupa. Płaszczyzna styka się z krawędzią ściany bocznej w punkcie R. Przekątne rombu przecinają się w punkcie O. Kąt między krawędzią a przekątną rombu wynosi $\alpha$.

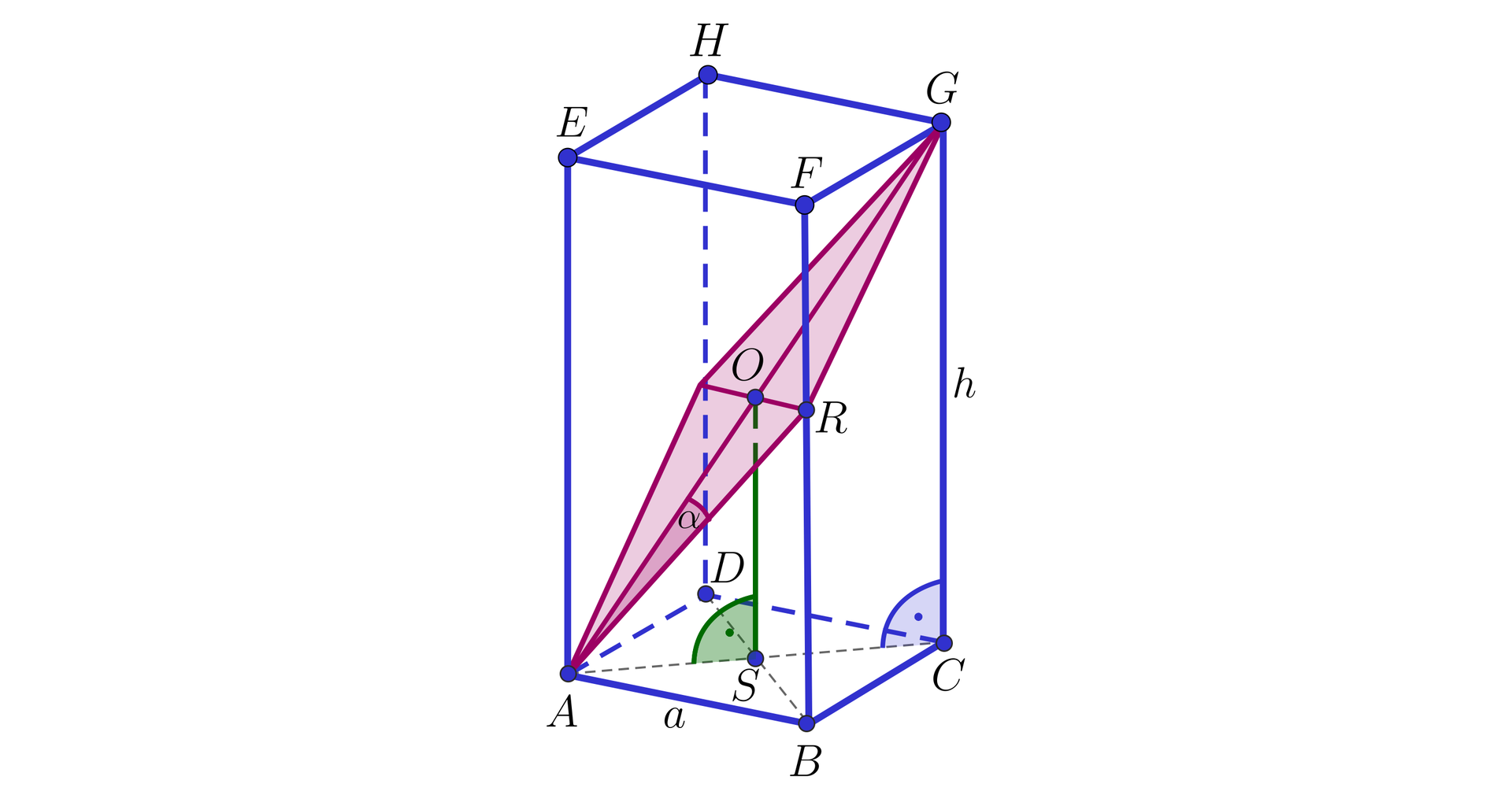
Aby obliczyć objętość graniastosłupa, musimy znaleźć zależność pomiędzy jego krawędzią podstawy a wysokością. Z treści zadania wiemy, że $\mathrm{tg}2\alpha =\sqrt{3}$, stąd wynika, że $\alpha =30°$. Następnie dla trójkąta $AOR$ (który jest prostokątny, bo przekątne rombu przecinają się pod kątem prostym) mamy $\mathrm{tg}30°=\frac{\left|OR\right|}{\left|AO\right|}$ oraz biorąc pod uwagę, że $\left|OR\right|=\frac{a\sqrt{2}}{2}$ otrzymujemy $\left|AO\right|=\frac{\sqrt{6}a}{2}$. Niech $\beta$ będzie kątem nachylenia przekroju do płaszczyzny podstawy. Z trójkąta $ASO$ mamy $\cos \beta =\frac{\left|AS\right|}{\left|AO\right|}$ oraz biorąc pod uwagę, że $\left|AS\right|=\frac{a\sqrt{2}}{2}$ i $\left|AO\right|=\frac{\sqrt{6}a}{2}$ otrzymujemy, że $\cos \beta =\frac{\sqrt{3}}{3}$, stąd $\sin \beta =\frac{\sqrt{6}}{3}$ i $\mathrm{tg}\beta =\sqrt{2}=\frac{h}{a\sqrt{2}}$. Zatem $h=2a$. Objętość graniastosłupa jest równa $V=a^{2}h=2a^3$.

Odcinek długości $d$ łączy środek krawędzi podstawy graniastosłupa prawidłowego czworokątnego z wierzchołkiem drugiej podstawy leżącym w tej samej płaszczyźnie ściany bocznej graniastosłupa. Pole boczne tego graniastosłupa jest równe $4d^2$. Wyznaczymy objętość tego graniastosłupa.

Rozwiązanie

Rozważmy graniastosłup prawidłowy czworokątny przedstawiony na rysunku.

RCI63VKgmssHY

Ilustracja przedstawia graniastosłup prawidłowy czworokątny A B C D E F G H, krawędzie podstawy mają długość a, a wysokość długość h. Z punktu F poprowadzono prostą przecinającą krawędź podstawy w punkcie S. dzieli on krawędź podstawy na pół. Odcinek F S leży na ścianie bocznej tego graniastosłupa.

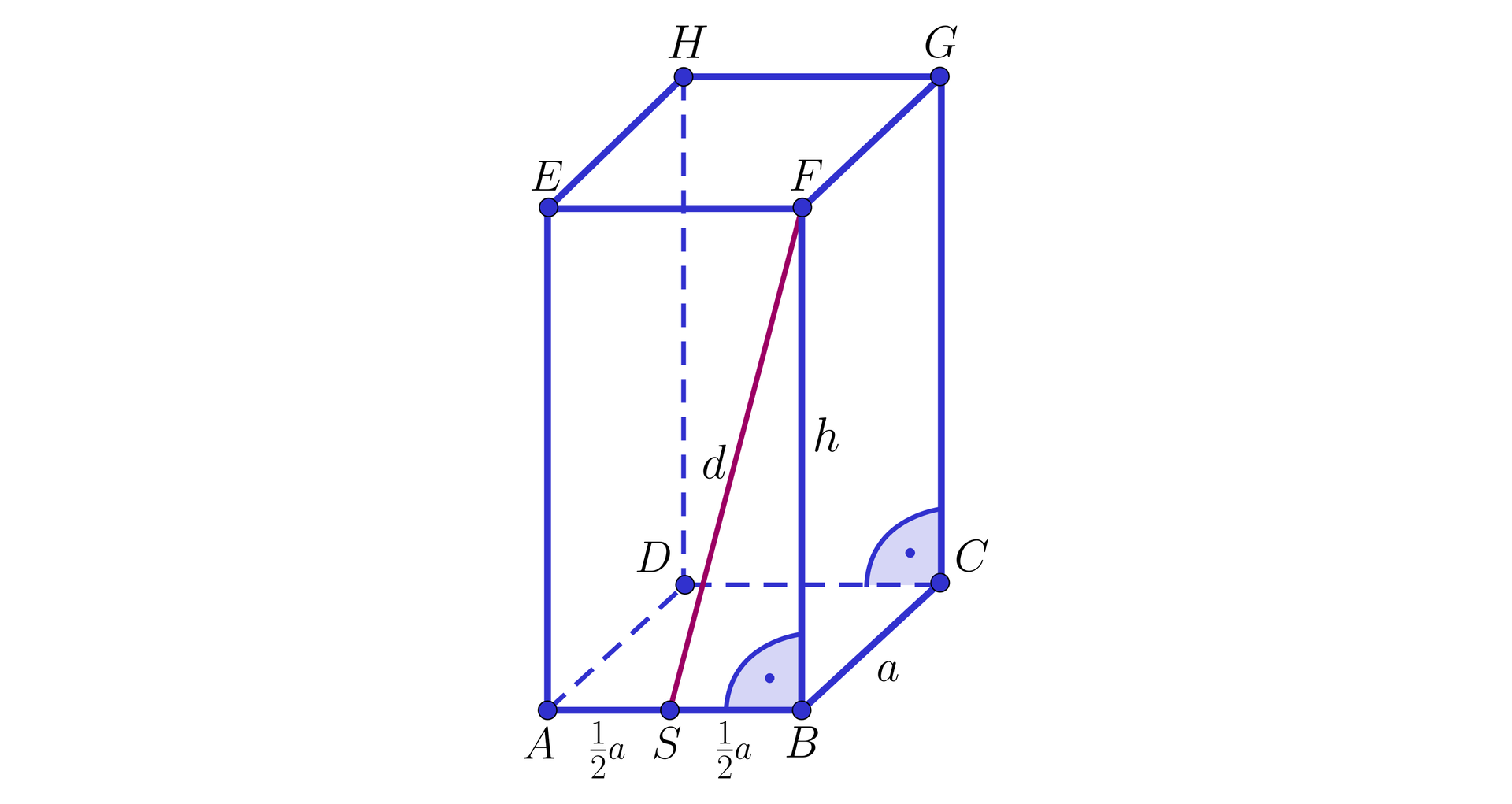
Z treści zadania wiemy, że pole boczne graniastosłupa jest równe $4d^2$, zatem mamy $4ah=4d^2$, a stąd otrzymujemy, że $d^2=ah$. Korzystając z  Twierdzenia Pitagorasa dla trójkąta $SBF$ otrzymujemy $d^2=\frac{1}{4}{a}^2+h^2$. Podstawiając $d^2=ah$ otrzymujemy $ah=\frac{1}{4}{a}^2+h^2$. Przekształcając to równanie otrzymujemy $a^2-4ah+4h^2=0$. Korzystając ze wzoru skróconego mnożenia na kwadrat  różnicy $a^2-2ab+b^2={\left(a-b\right)}^2$, nasze równanie przyjmuje postać ${\left(a-2h\right)}^2=0$. Łatwo zauważyć, że równość ta zachodzi tylko wtedy gdy $a=2h$. Zatem otrzymujemy $d^2=2h^2$, z czego wynika, że $d=\sqrt{2}h$, czyli $h=\frac{\sqrt{2}}{2}d$ oraz $a=\sqrt{2}d$. Możemy obliczyć szukaną objętość: $V=2d^2·\frac{\sqrt{2}}{2}d=\sqrt{2}{d}^3$.

Z punktu przecięcia przekątnych podstawy graniastosłupa prawidłowego czworokątnego poprowadzono odcinki o długości $d$ do dwóch wierzchołków drugiej podstawy, przy czym wierzchołki te nie należą do tej samej płaszczyzny ściany bocznej. Kosinus kąta między nimi jest równy $\frac{1}{4}$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie

Rozważmy graniastosłup prawidłowy czworokątny przedstawiony na rysunku.

R1Dj27nWwWXPM

Ilustracja przedstawia graniastosłup prawidłowy czworokątny A B C D E F G H, krawędzie podstawy mają długość a, a wysokość długość h. Przekątne podstawy graniastosłupa przecinają się w punkcie S. Z wierzchołka H i F poprowadzono dwie proste o spotykające się w punkcie S. Kąt między prostymi wynosi $\alpha$.

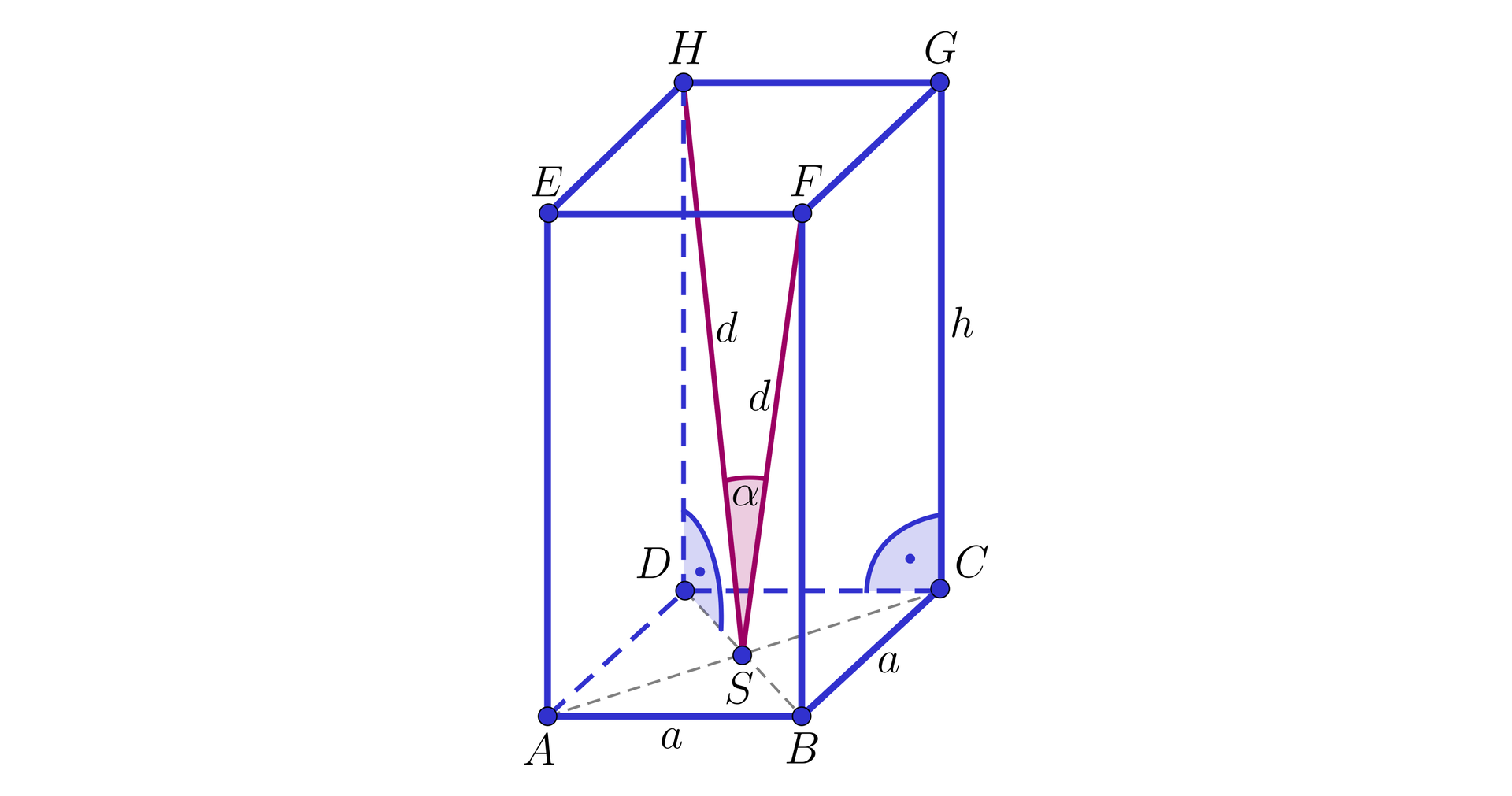
Niech $a$ oznacza długość krawędzi podstawy, a $h$ długość wysokości rozważanego graniastosłupa. Korzystając z twierdzenia kosinusówtwierdzenie kosinusówtwierdzenia kosinusów dla trójkąta $HSF$ otrzymujemy $2a^2=2d^2-2d^2·\frac{1}{4}=2d^2-\frac{1}{2}{d}^2=\frac{3}{2}{d}^2$, stąd $a=\frac{\sqrt{3}}{2}d$. Korzystając z twierdzenia Pitagorasa dla trójkąta $HDS$ mamy $h^2+\frac{1}{2}{a}^2=d^2$. Podstawiając za $a=\frac{\sqrt{3}}{2}d$ otrzymujemy $h^2=\frac{5}{8}{d}^2$, czyli $h=\frac{\sqrt{10}}{4}d$. Możemy obliczyć szukaną objętość: $V=\frac{3}{4}{d}^2·\frac{\sqrt{10}}{4}d=\frac{3\sqrt{10}}{16}{d}^3$.

graniastosłup prosty, którego podstawą jest kwadrat

prostopadłościan, którego wszystkie krawędzie są równe

w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta

w dowolnym trójkącie, kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi