Przeczytaj

Odległość między prostymi równoległymiOdległość między prostymi równoległymi $k$ i $m$ to długość najkrótszego spośród odcinków, których jeden koniec należy do prostej $k$ , zaś drugi – do prostej $m$ . Łatwo zauważyć, że odcinek ten jest prostopadły do rozważanych prostych.

RWSkPC51PReTq

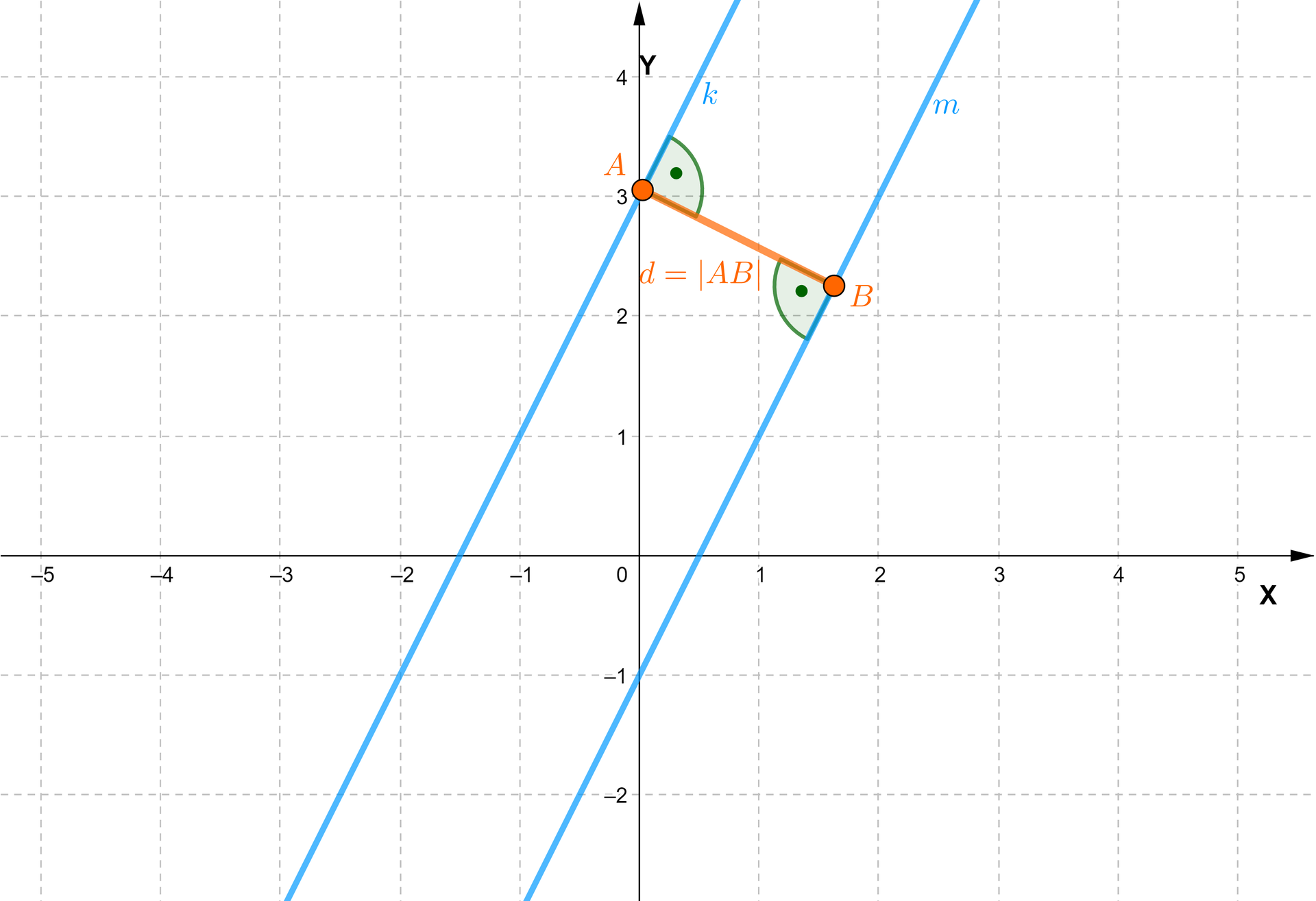
Ilustracja przedstawia dwuwymiarowy układ współrzędnych. Oś X ograniczona jest od -5 do 5, natomiast oś Y ograniczona jest od -2 do 4. Na układzie zaznaczone są dwie proste k oraz m, które są równoległe względem siebie. Zaznaczono odległość pomiędzy prostymi, miejsce, w którym styka się z prostą k oznaczono jako punkt A, natomiast miejsce, w którym styka się z prostą m, oznaczono jako punkt B. Pod odcinkiem AB zapisano matematycznie informację, że odległość pomiędzy prostymi jest równa długości odcinka AB.

Zaczniemy od rozwiązania prostego przykładu.

Przykład 1

Obliczymy odległość między prostymi o równaniach $m : y = 2 x - 1$ oraz $k : y = 2 x + 3$ .

R1UnXq5nqKPjJ

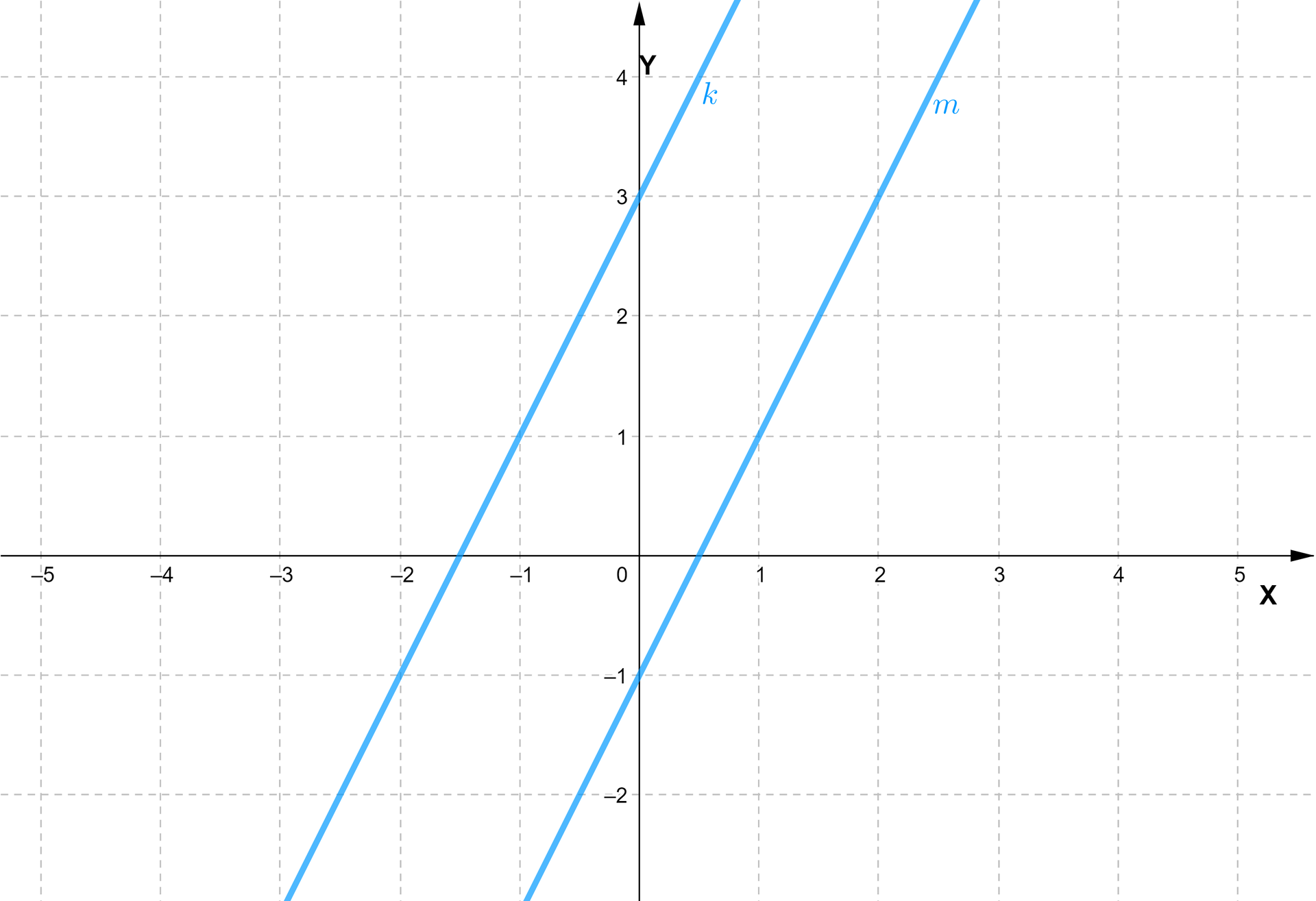
Ilustracja przedstawia dwuwymiarowy układ współrzędnych. Najmniejsza wartość na osi X to -5, a największa 5, natomiast na osi Y najmniejsza wartość wynosi -2, a największa 4. Na układzie zaznaczone są dwie proste równoległe względem siebie k oraz m. Prosta k przecina oś X mniej więcej w punkcie -2;0, a prosta m przecina oś X blisko punktu 0;0.

Często popełniany błąd w tego typu zadaniach polega na zinterpretowaniu odległości między prostymi jako różnicy między wyrazami wolnymi obu prostych, z czego wynikałoby, że odległość między danymi prostymi jest równa $4$ . Wykorzystany do tego rachunku odcinek nie jest najkrótszy z możliwych, równoważnie – nie jest prostopadły do rozważanych prostych.

R1syEJLHM74iY

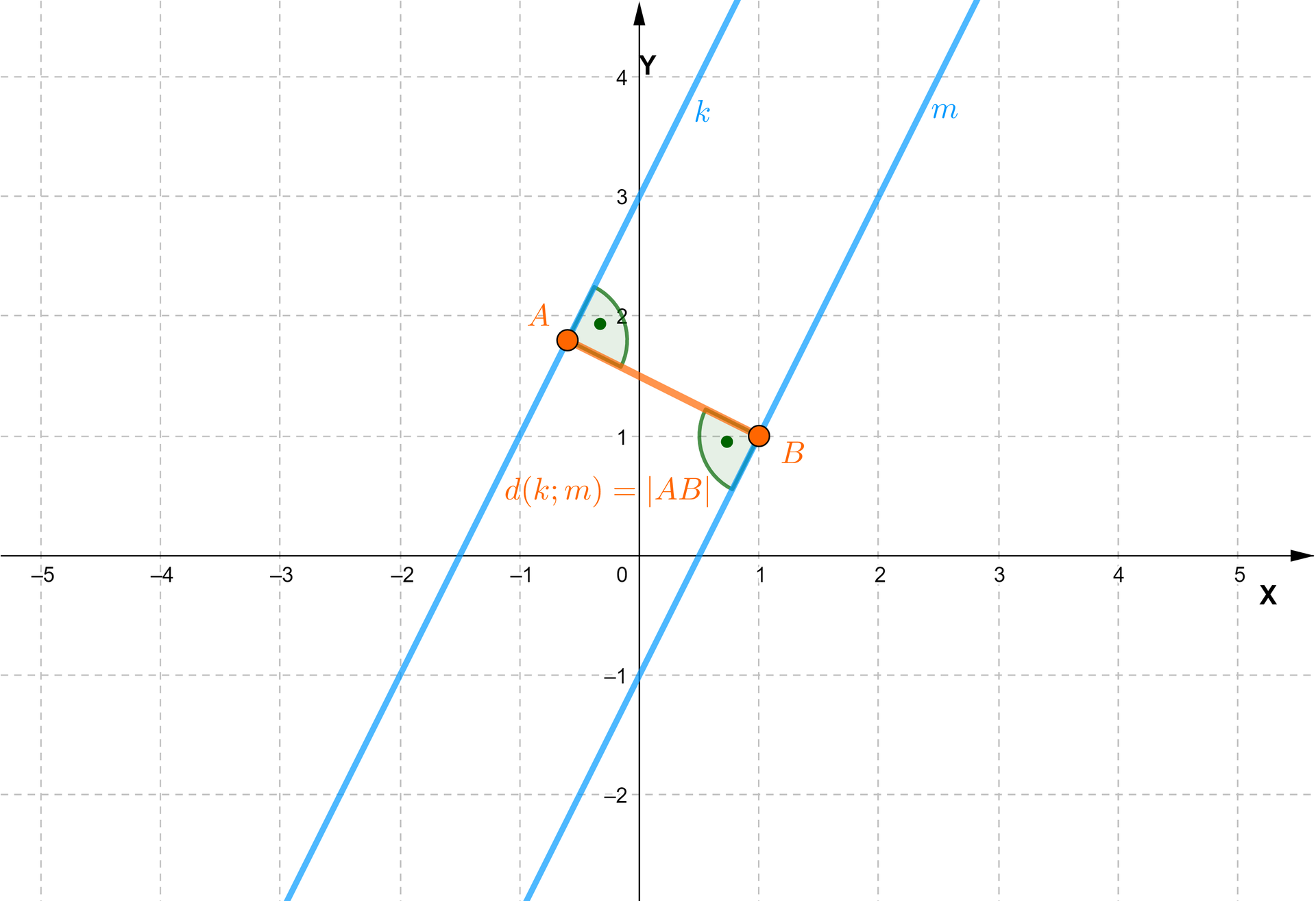
Ilustracja przedstawia dwuwymiarowy układ współrzędnych z osią X od -5 do 5 oraz osią Y od -2 do 4. Zaznaczono dwie proste równoległe względem siebie k oraz m, na ilustracji jest również prostopadły do obu prostych odcinek AB, który jest odległością pomiędzy dwiema prostymi. Pod odcinkiem AB zapisano matematycznie informację, że odległość pomiędzy prostymi jest równa długości odcinka AB.

W celu obliczenia rzeczywistej odległości między prostymi wybierzemy punkt na prostej $k$ , niech będzie to punkt $A$ o współrzędnych $(0, 3)$ , i skorzystamy ze wzoru na odległość punktu od prostej (w tym przypadku od prostej $m : 2 x - y - 1 = 0$ ):

d (k, m) = d (A, m) = \frac{|2 \cdot 0 - 3 - 1|}{\sqrt{2^{2} + {(- 1)}^{2}}} = \frac{4}{\sqrt{5}} = \frac{4 \sqrt{5}}{5}

Zatem odległość między prostymi o równaniach $y = 2 x - 1$ oraz $y = 2 x + 3$ jest równa $\frac{4 \sqrt{5}}{5}$ .

Wykorzystując pomysł zawarty w powyższym przykładzie wyprowadzimy teraz wzór na odległość między prostymi równoległymiproste równoległeprostymi równoległymi opisanymi równaniami ogólnymi.

Rozważmy proste $k : A x + B y + C = 0$ oraz $m : A_{1} x + B_{1} y + C_{1} = 0$ . Ponieważ proste te mają być równoległe, więc współczynniki przy zmiennych w jednym równaniu są proporcjonalne do współczynników przy odpowiednich zmiennych w drugim równaniu.

Po podzieleniu drugiego równania przez współczynnik proporcjonalności otrzymamy równanie o współczynnikach przy zmiennych równych $A$ i $B$ .

Możemy zatem przyjąć, że proste mają równania $k : A x + B y + C = 0$ oraz $m : A x + B y + D = 0$ , które różnią się tylko wyrazami wolnymi.

Wybierzmy punkt $A = (x_{0}, y_{0})$ należący do prostej $k$ . Ponieważ $A$ leży na prostej $k$ , więc jego współrzędne spełniają równanie prostej $k$ . Zachodzi więc równość $A x_{0} + B y_{0} + C = 0$ , która jest równoważna równości $A x_{0} + B y_{0} = - C$ . Skorzystajmy teraz ze wzoru na odległość punktu od prostej:

d (A, m) = \frac{|A x_{0} + B y_{0} + D|}{\sqrt{A^{2} + B^{2}}}

Ponieważ $A x_{0} + B y_{0} = - C$ , więc powyższe wyrażenie przyjmuje postać

d (A, m) = \frac{|A x_{0} + B y_{0} + D|}{\sqrt{A^{2} + B^{2}}} = \frac{|- C + D|}{\sqrt{A^{2} + B^{2}}} = \frac{|C - D|}{\sqrt{A^{2} + B^{2}}}

Ważne!

Zatem wzór na odległość prostych równoległych o równaniach $k : A x + B y + C = 0$ oraz $m : A x + B y + D = 0$ to

d (k, m) = \frac{| C - D |}{\sqrt{A^{2} + B^{2}}}

Przykład 2

Obliczymy odległość między prostymi o równaniach $k : 3 x + 5 y - 2 = 0$ oraz $m : 6 x + 10 y + 7 = 0$ . Zauważmy najpierw, że współczynniki przy odpowiednich zmiennych w obu równaniach są proporcjonalne.

Po podzieleniu drugiego równania obustronnie przez $2$ otrzymujemy równanie $m : 3 x + 5 y + 3, 5 = 0$ . Teraz możemy już zastosować wzór na odległość między prostymi równoległymi:

d (k, m) = \frac{|- 2 - 3, 5|}{\sqrt{3^{2} + 5^{2}}} = \frac{5, 5}{\sqrt{34}} = \frac{5, 5 \sqrt{34}}{34} = \frac{11 \sqrt{34}}{68}

Przykład 3

Wyznaczymy wartości parametru $m$ tak, aby odległość między prostymi o równaniach $k : x - 2 y + 3 = 0$ oraz $l : - 2 x + 4 y + m = 0$ była równa $5$ .

Zauważmy, że proste $k$ i $l$ są równoległe gdyż $1 \cdot 4 = - 2 \cdot (- 2)$ . Po pomnożeniu obu stron pierwszego równania przez $(- 2)$ otrzymujemy równanie $k : - 2 x + 4 y - 6 = 0$ . Ze wzoru na odległość między prostymi równoległymiodległość między prostymi równoległymi wynika równanie:

5 = d (k, l) = \frac{|- 6 - m|}{\sqrt{{(- 2)}^{2} + 4^{2}}}

które można przekształcić kolejno do:

5 \sqrt{20} = |m + 6|

10 \sqrt{5} = |m + 6|

Powyższe równanie jest równoważne alternatywie:

m + 6 = 10 \sqrt{5}

lub

m + 6 = - 10 \sqrt{5}

Zatem szukane wartości parametru $m$ to $10 \sqrt{5} - 6$ oraz $- 10 \sqrt{5} - 6$ .

Przykład 4

Obliczymy pole pięciokąta ograniczonego prostymi o równaniach
$k : y = x + 5$ ,
$l : y = 7$ ,
$m : y = x - 8$ ,
$n : y = - \frac{1}{2} x + 10$ ,
$p : y = - \frac{1}{2} x - 2$ .

Rozwiązując kolejno układy równań

\{\begin{cases} y = x + 5 \\ y = 7 \end{cases}

\{\begin{cases} y = 7 \\ y = - \frac{1}{2} x + 10 \end{cases}

\{\begin{cases} y = - \frac{1}{2} x + 10 \\ y = x - 8 \end{cases}

\{\begin{cases} y = x - 8 \\ y = - \frac{1}{2} x - 2 \end{cases}

\{\begin{cases} y = - \frac{1}{2} x - 2 \\ y = x + 5 \end{cases}

Otrzymujemy odpowiednio współrzędne wierzchołków pięciokąta:

$A = (2, 7)$ , $B = (6, 7)$ , $C = (12, 4)$ , $D = (4, - 4)$ , $E = (- \frac{14}{3}, \frac{1}{3})$

Zauważmy, że czworokąt $A C D E$ jest trapezem o podstawach $C D$ i $A E$ . Jego wysokość $h$ możemy obliczyć korzystając ze wzoru na odległość między prostymi równoległymiproste równoległeprostymi równoległymi:

h = d (p r . C D, p r . A E) = \frac{|- 8 - 5|}{\sqrt{1^{2} + 1^{2}}} = \frac{13}{\sqrt{2}} = \frac{13 \sqrt{2}}{2}

Podstawy zaś mają długości:

|C D| = \sqrt{{(12 - 4)}^{2} + {(4 - (- 4))}^{2}} = \sqrt{64 + 64} = 8 \sqrt{2}

|A E| = \sqrt{{(- \frac{14}{3} - 2)}^{2} + {(\frac{1}{3} - 7)}^{2}} = \sqrt{\frac{400}{9} + \frac{400}{9}} = \frac{20 \sqrt{2}}{3}

Zatem pole trapezu $A C D E$ jest równe

P_{A C D E} = \frac{8 \sqrt{2} + \frac{20 \sqrt{2}}{3}}{2} \cdot \frac{13 \sqrt{2}}{2} = \frac{286}{3}

Pozostaje obliczyć pole trójkąta $A C B$ . W tym celu wystarczy obliczyć długość odcinka $B C$ i odległość punktu $A$ od prostej $B C$ :

|B C| = \sqrt{{(6 - 12)}^{2} + {(7 - 4)}^{2}} = \sqrt{36 + 9} = 3 \sqrt{5}

d (A, p r . B C) = \frac{|2 + 2 \cdot 7 - 20|}{\sqrt{1 + 4}} = \frac{4}{\sqrt{5}} = \frac{4 \sqrt{5}}{5}

P_{A C B} = \frac{1}{2} \cdot 3 \sqrt{5} \cdot \frac{4 \sqrt{5}}{5} = 6

Zatem pole rozważanego pięciokąta jest równe

P_{A B C D E} = \frac{286}{3} + 6 = \frac{304}{3}

Słownik

proste równoległe

w geometrii euklidesowej są to proste, które nie mają punktów wspólnych

odległość między prostymi równoległymi

długość najkrótszego spośród odcinków $A B$ , którego koniec $A$ znajduje się na jednej z prostych, zaś koniec $B$ na drugiej; odcinek $A B$ jest prostopadły do każdej z rozważanych prostych równoległych

Wprowadzenie

Aplet

Słownik