Przeczytaj
Stożek wpisany w kulę
Wyobraźmy sobie stożek wpisany w kulę. Jakie warunki muszą być spełnione, aby stożek wpisać w kulę? W jaki sposób wykreślić stożek wpisany w kulę na kartce papieru? W odpowiedzi na te pytania pomoże nam aplet Geogebry.
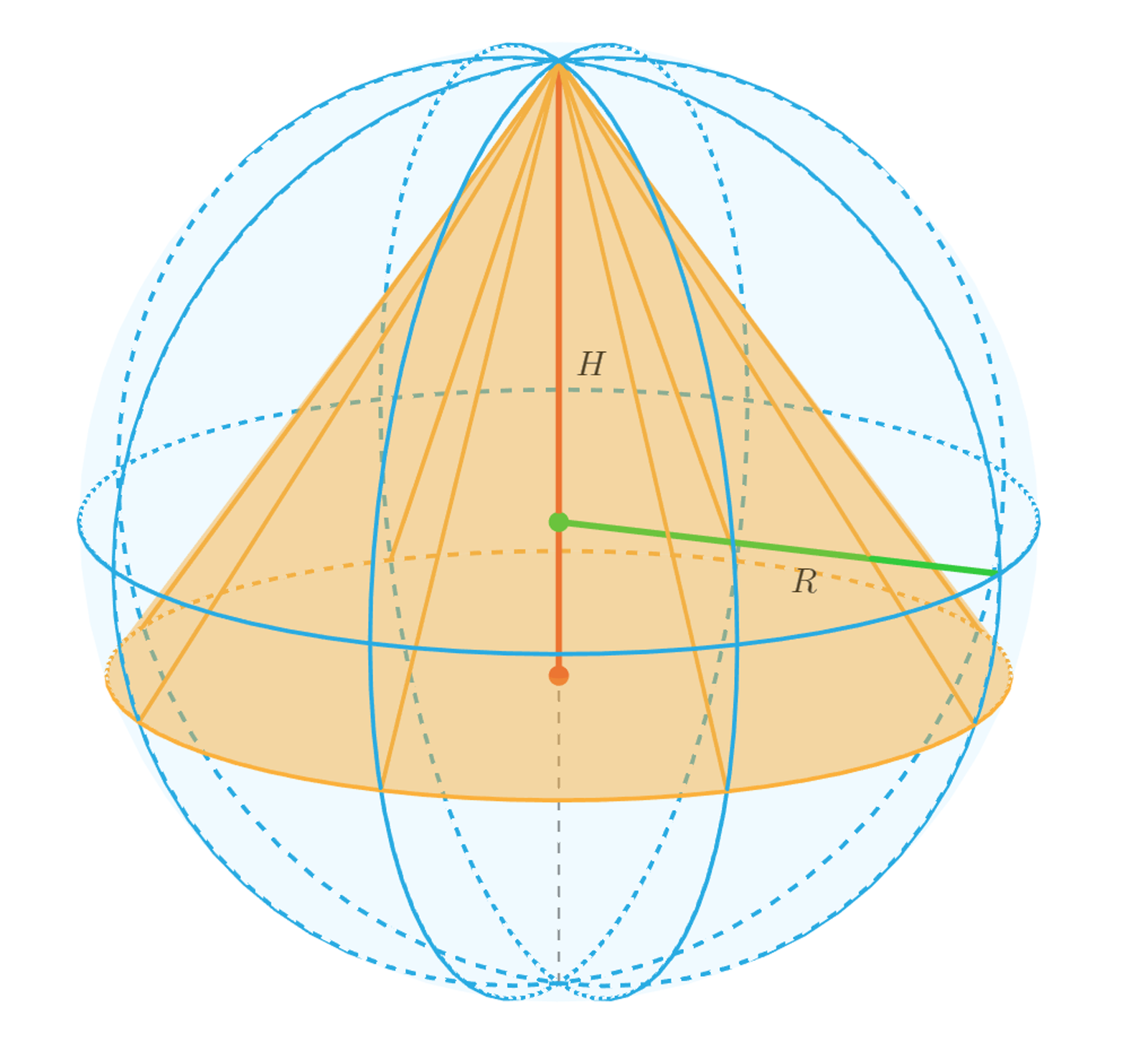
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DAunAltdB
Zapamiętaj:
Stożek jest wpisany w kulę wtedy i tylko wtedy, gdy wierzchołek stożka należy do sfery kuli oraz okrąg podstawy stożka zawiera się w sferze tej kuli.
Zadania dotyczące stożka wpisanego w kulę można sprowadzić do prostych zadań geometrii płaskiej. Na rysunku poniżej przedstawiono przekrój osiowy stożkaprzekrój osiowy stożka wpisanego w kulę. Przekrój osiowy tych brył jest kołem opisanym na trójkącie równoramiennym. Spostrzeżenie to pomoże nam w uproszczeniu planowania strategii rozwiązania wielu zadań geometrii przestrzennej.
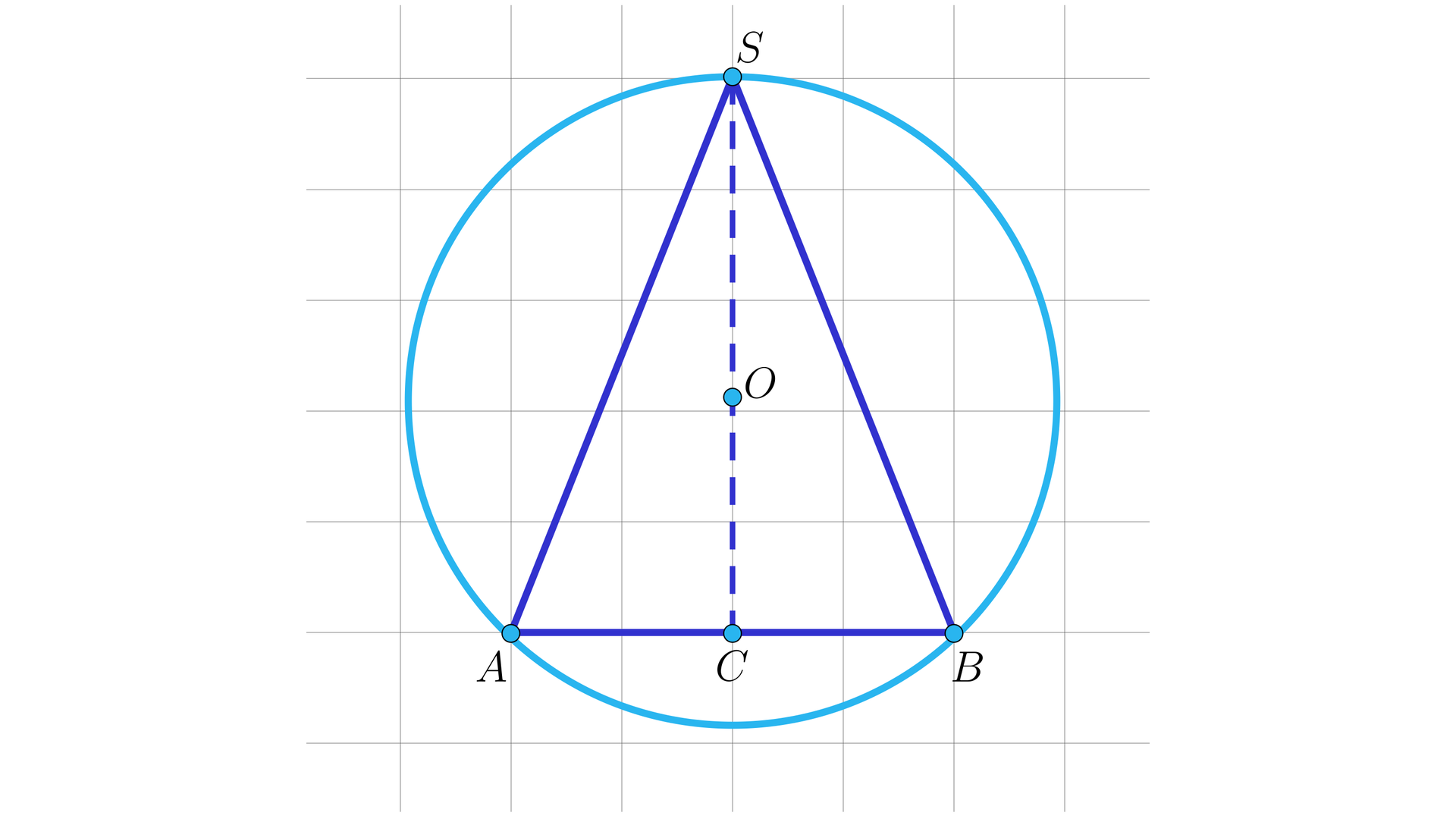
Dla przejrzystości rysunku, przekrój osiowy kuliprzekrój osiowy kuli wystarczy wykreślić jako okrąg.
Tak wykreślony rysunek jest punktem startowym w planowaniu kolejnych kroków. Ważnym elementem rozwiązania zadania jest analiza własności otrzymanych figur oraz związków miarowych zachodzących między odpowiednimi odcinkami. Do rozwiązania zadań dotyczących stożka wpisanego w kulę wykorzystamy znane nam twierdzenia geometrii płaskiej.
Rozważmy przekrój osiowy stożka wpisanego w kulę. Przyjmijmy oznaczenia jak na rysunku. Określimy najważniejsze związki miarowe zachodzące pomiędzy odpowiednimi odcinkami tworzącymi przekrój osiowy tych brył.
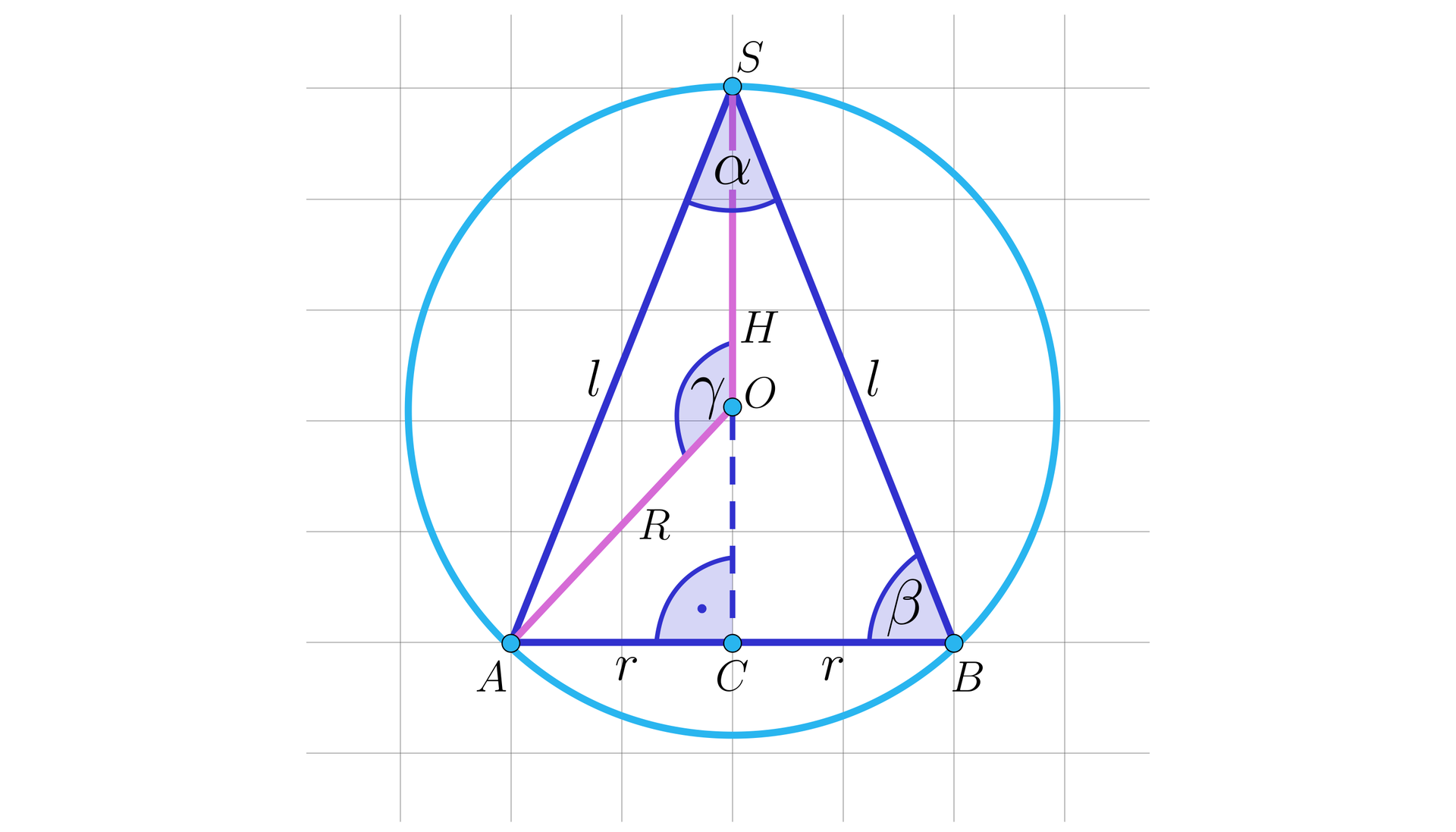
długość wysokości stożka
długość promienia podstawy stożka
długość tworzącej stożka
kąt rozwarcia stożka
kąt nachylenia tworzącej stożka do płaszczyzny podstawy stożka
długość promienia kuli
Zauważmy, że
z twierdzenia sinusów
z zależności między kątem środkowym i wpisanym opartym na tym samym łuku
z twierdzenia Pitagorasa
lub z twierdzenia cosinusówtwierdzenia cosinusów.
Stożek wpisano w kulę. Kąt nachylenia tworzącej stożka do płaszczyzny podstawy stożka ma miarę . Uzasadnij, że długość tworzącej stożka jest równa długości promienia kuli.
Rozwiązanie
Wykreślamy rysunek i przyjmujemy oznaczenia. Środek kuli nie należy do stożka, ponieważ trójkąt , będący przekrojem osiowym stożka, jest rozwartokątny.
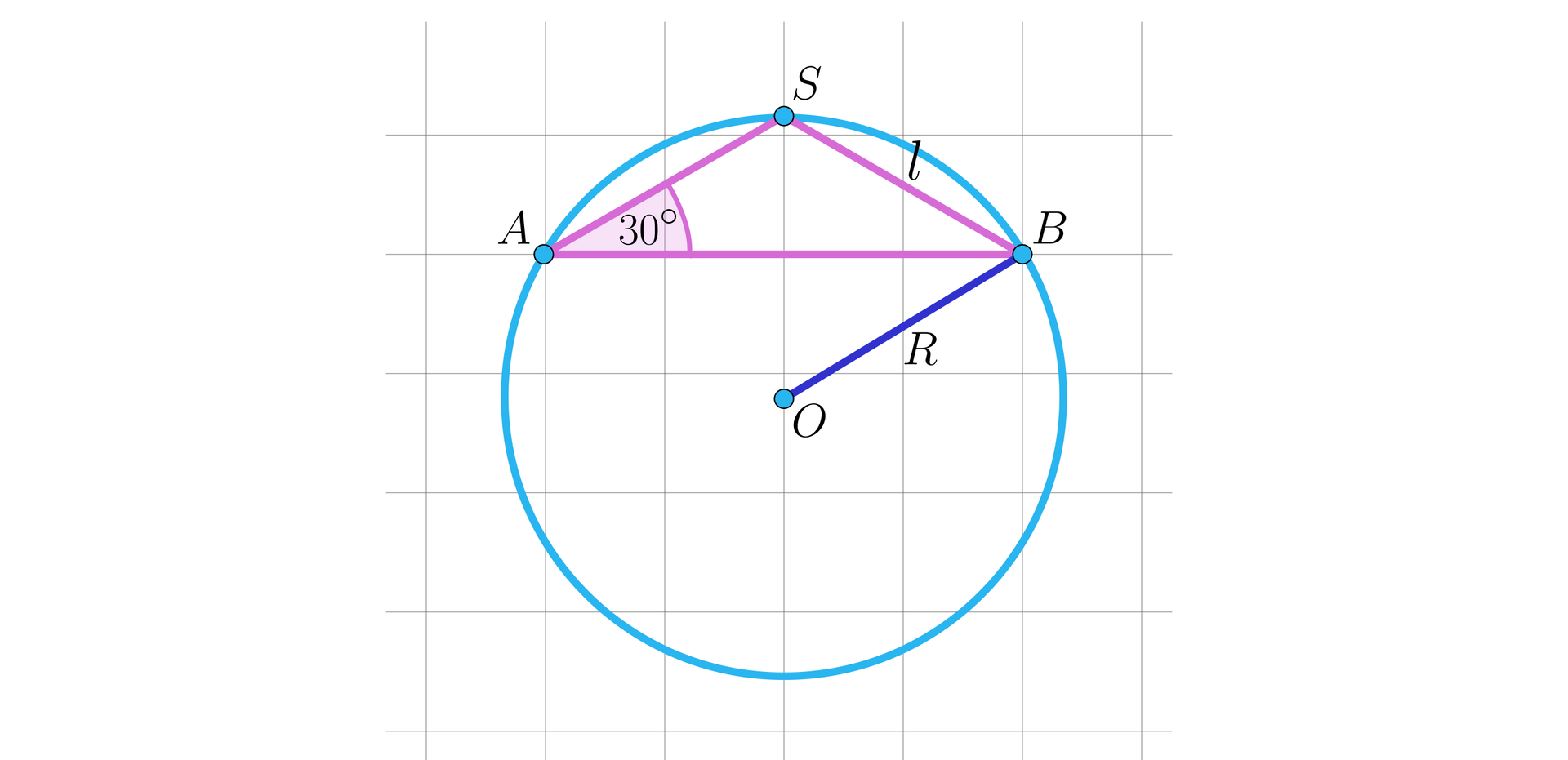
długość promienia kuli
długość tworzącej stożka
miara kąta nachylenia tworzącej stożka do płaszczyzny podstawy stożka.
Zadanie rozwiążemy dwoma metodami.
I metoda wykorzystamy twierdzenie sinusówtwierdzenie sinusów.
, zatem , a stąd mamy co należało wykazać.
II metoda Na rysunku wykreślmy dodatkowo promień . Zauważmy, że kąt jest kątem środkowym opartym na tym samym łuku co kąt wpisany .
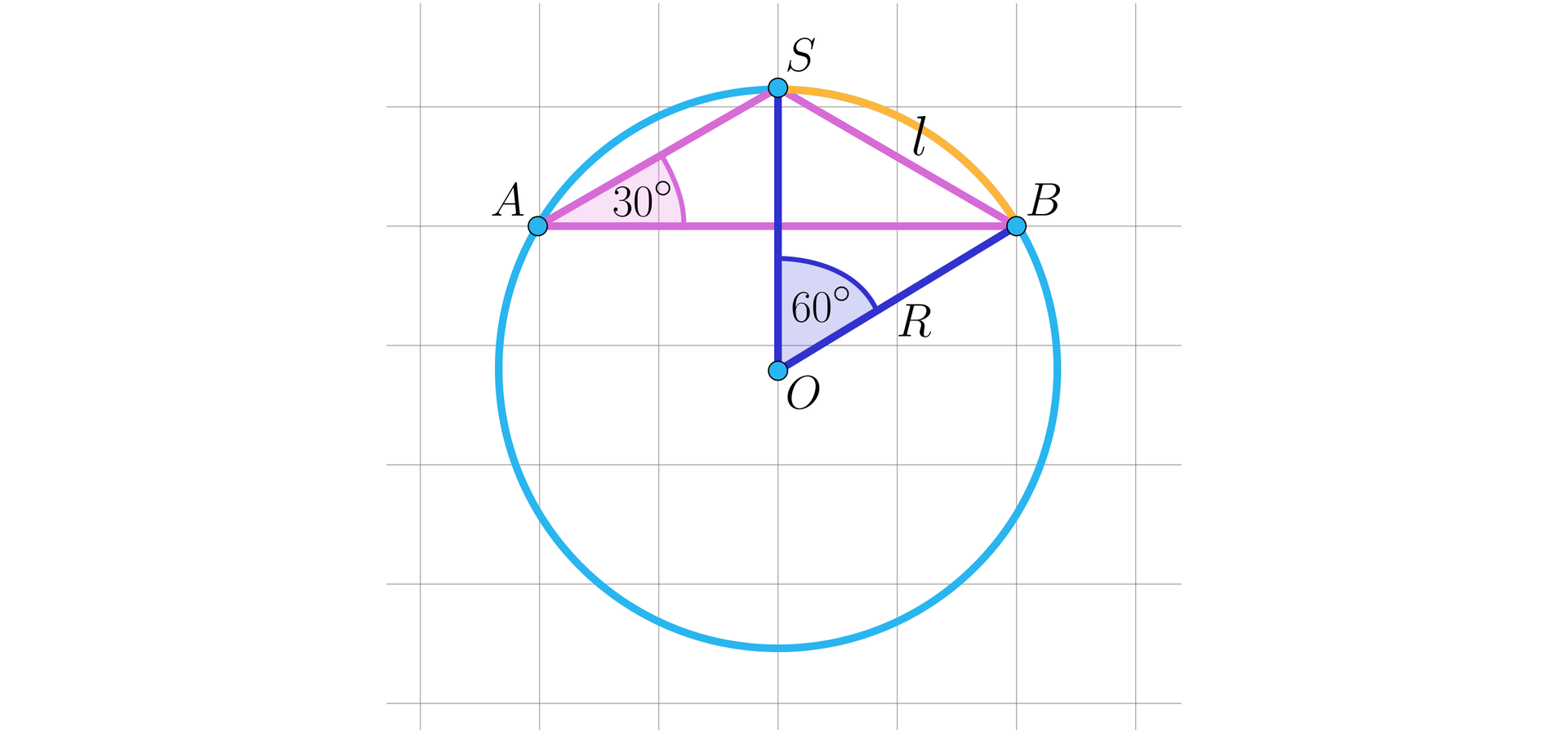
Wynika stąd, że , ponadto trójkąt jest trójkątem równoramiennym, zatem trójkąt jest trójkątem równobocznym. Stąd mamy , co należało wykazać.
Stosunek długości wysokości stożka wpisanego w kulę do długości promienia tej kuli wynosi . Oblicz stosunek objętości stożka do objętości kuli.
Rozwiązanie
Wykreślamy rysunek obrazujący przekrój osiowy stożka wpisanego w kulę. Z warunków zadania wynika, że środek kuli zawiera się w stożku, ponieważ wyskość stożka jest dłuższa niż promień tej kuli.
Przyjmujemy oznaczenia. Oznaczenia pomogą w prowadzeniu toku rozumowania.
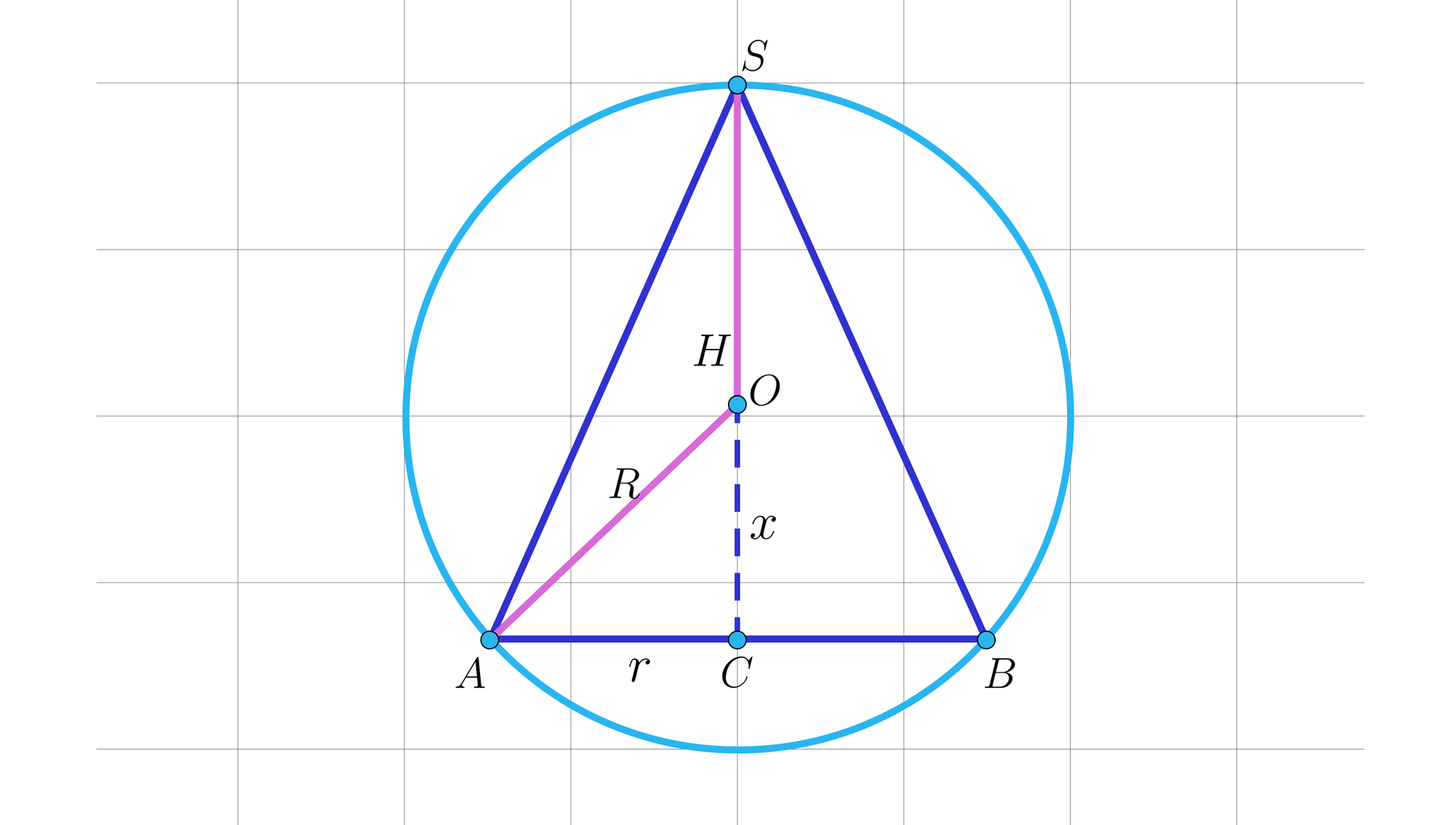
długość wysokości stożka
długość promienia kuli
długość promienia podstawy stożka
długość odcinka .
Z warunków zadania mamy , stąd .
Zapisujemy wzór opisujący odpowiedni stosunek .
Uzależnimy długość promienia podstawy stożka od długości promienia kuli. Korzystamy z twierdzenia Pitagorasa dla trójkąta .
wiedząc, że otrzymujemy zależność
, stąd
, dalej
z warunków zadania mamy , zatem
.Wynika stąd, że .
W kulę wpisano stożek. Długość promienia kuli jest dwa razy dłuższa od długości promienia podstawy stożka. Wyznacz miarę kąta rozwarcia stożka.
Rozwiązanie
Rozwiązanie zadania zaczynamy od wykonania czytelnego rysunku i przyjęcia oznaczeń.
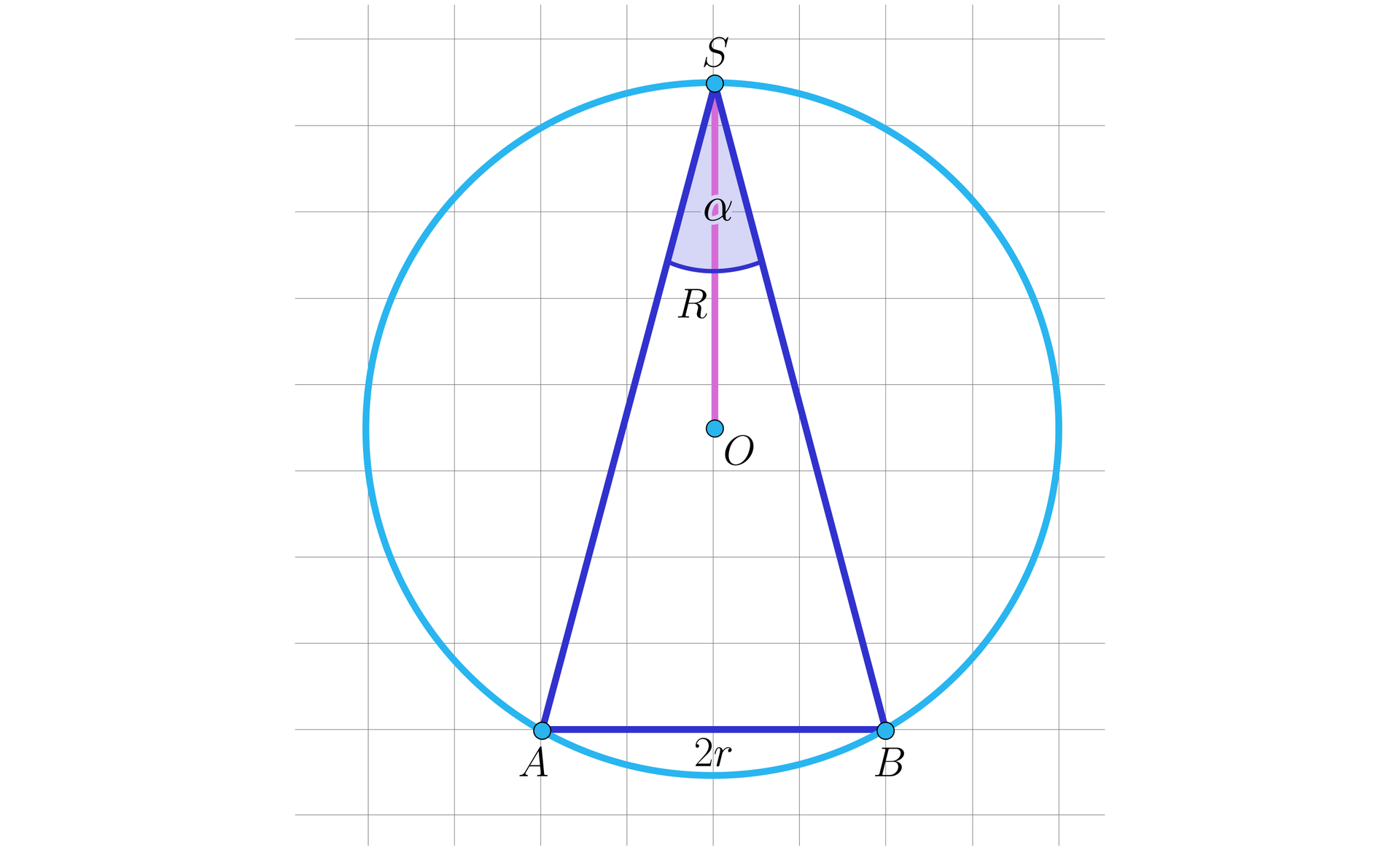
długość promienia kuli
długość średnicy podstawy stożka
miara kąta rozwarcia stożka
z warunków zadania mamy:
.
Zauważmy, że mając określoną zależność pomiędzy długością promienia kuli i długością średnicy stożka, do wyznaczenia miary kąta rozwarcia stożka możemy wykorzystać twierdzenie sinusów dla trójkąta .
Układamy twierdzenie sinusów dla trójkąta
Korzystamy z zależności podanej w zadaniu , stąd otrzymujemy
, zatem
, stąd
.Wyznaczamy miarę kąta, dla którego .
Wiemy, że kąt rozwarcia stożka jest kątem z przedziału , zatem rozwiązaniem naszego równania jest kąt lub kąt .Istnieją dwa rozwiązania tego zadania.
W kulę o promieniu długości wpisano stożek, którego kąt rozwarcia ma miarę . Oblicz pole powierzchni bocznej tego stożka.
Rozwiązanie
Wykreślamy przekrój osiowy tych brył i przyjmujemy oznaczenia.
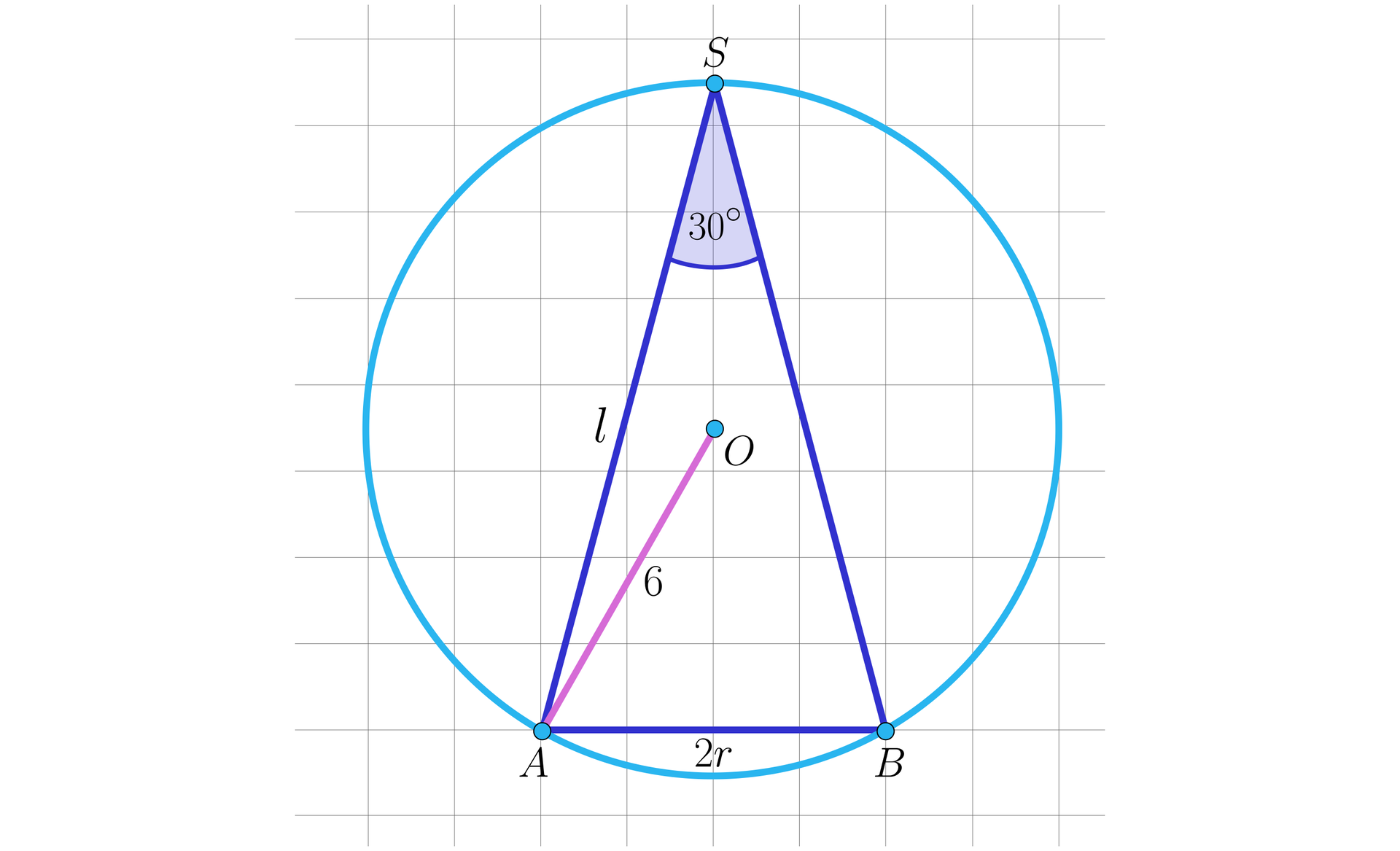
długość średnicy podstawy stożka
długość promienia kuli
długość tworzącej stożka
pole powierzchni bocznej stożka.
Do wyznaczenia długości promienia podstawy stożka oraz długości tworzącej stożka wykorzystamy twierdzenie sinusów dla trójkąta .
Z twierdzenia sinusów otrzymamy zależność
, stąd , zatem .Długość tworzącej stożka możemy obliczyć korzystając z twierdzenia cosinusów dla trójkąta albo dla trójkąta .
I metoda, korzystamy z trójkąta .
Z twierdzenia cosinusów otrzymamy zależność
, stąd , zatem ,
a stąd wynika, że , dalej po usunięciu niewymierności z mianownika otrzymujemy , zatem .
II metoda, korzystamy z trójkąta . Zauważamy, że kąt nachylenia tworzącej stożka do płaszczyzny podstawy stożka ma miarę , zatem kąt ma miarę .
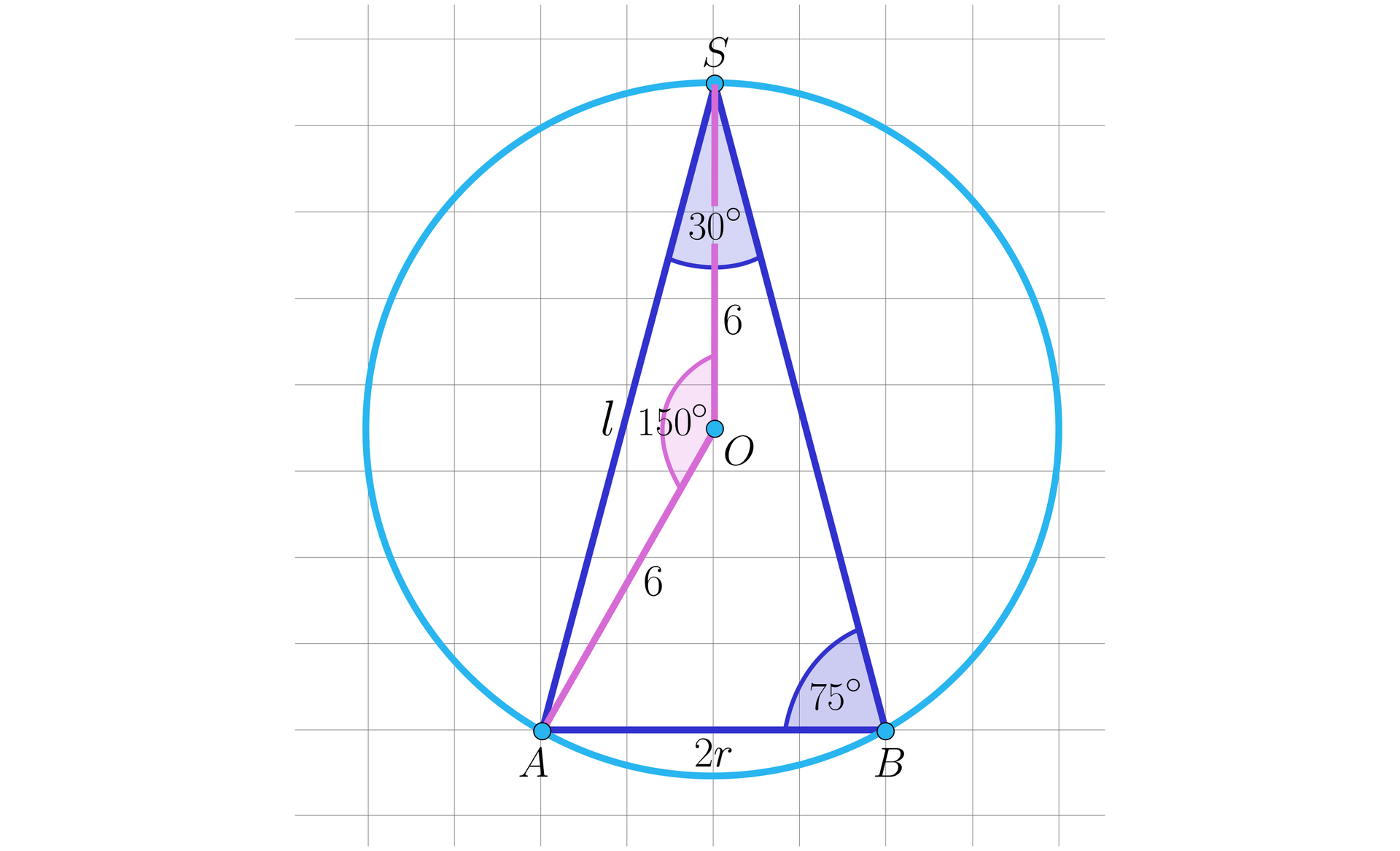
Korzystając z twierdzenia cosinusówtwierdzenia cosinusów dla trójkąta , otrzymujemy
, zatem
, stąd
, zatem
.
Obliczamy pole powierzchni bocznej stożka. , zatem ostatecznie otrzymujemy .
W kulę wpisano stożek o objętości równej objętości kuli. Wysokość stożka ma długość . Wyznacz długość promienia kuli.
Rozwiązanie
Wykreślamy rysunek i przyjmujemy oznaczenia.
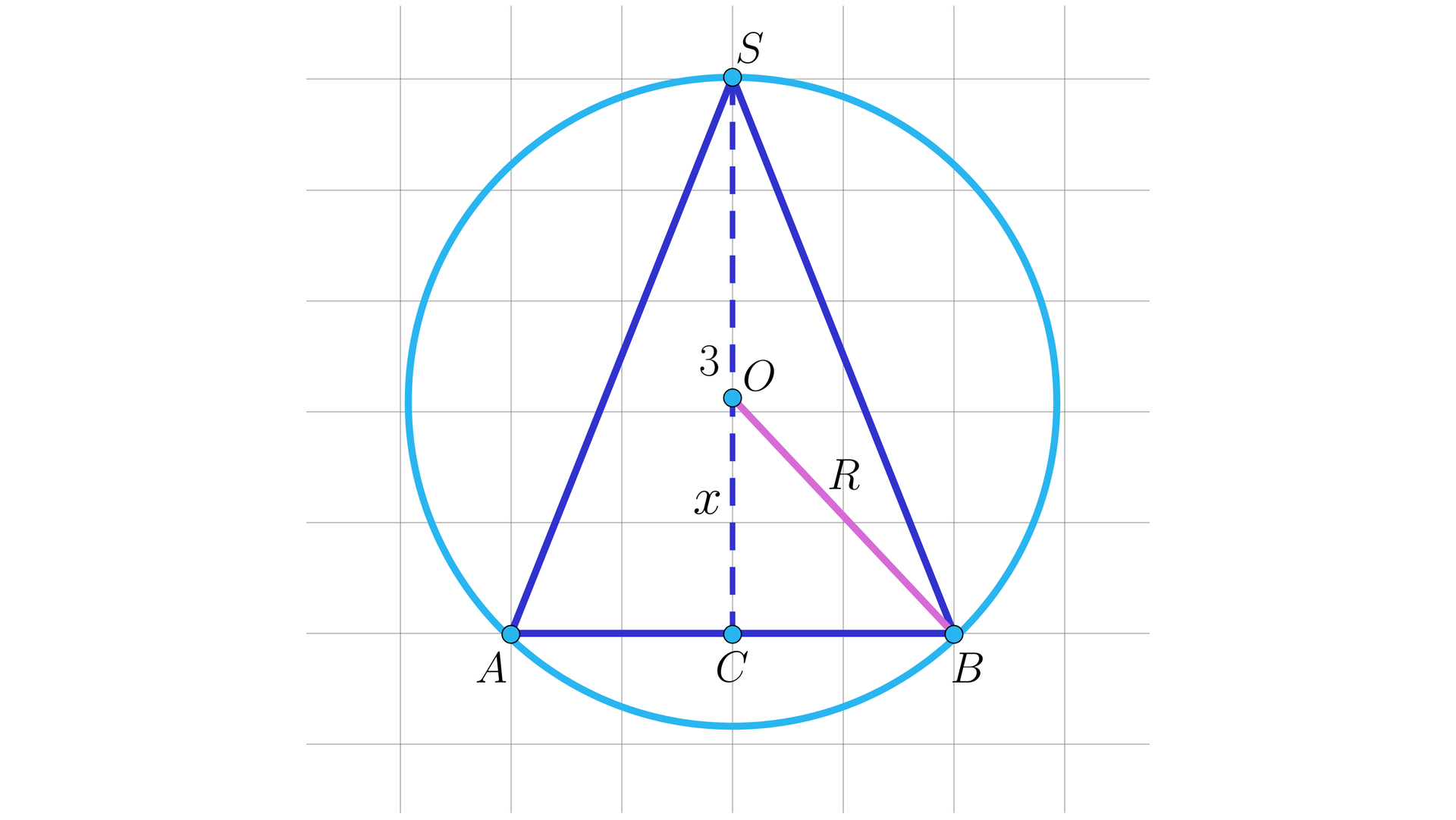
długość wysokości stożka
długość promienia kuli
długość odcinka
warunki zadania.
Z warunków zadania , mamy odpowiednio zależność , gdzie oznacza długość promienia podstawy stożka. Upraszczając zależność otrzymujemy
, stąd .Długość promienia kuli możemy wyznaczyć z trójkąta , korzystając z twierdzenia Pitagorasa.
, gdzie .
Zatem odpowiednio podstawiając, otrzymamy równanie
, stąd
, zatem
. Otrzymaliśmy równanie stopnia trzeciego z niewiadomą .Zauważmy, że pierwiastkiem równania jest liczba , ponieważ .
Rozkładając lewą stronę równania na czynniki, otrzymujemy
. Wynika stąd, że lub lub , ponieważ , jako długość odcinka, to otrzymujemy dwa rozwiązania
lub .
Słownik
przekrój stożka płaszczyzną zawierającą oś obrotu stożka. Przekrój osiowy stożka jest trójkątem równoramiennym
przekrój kuli płaszczyzną zawierającą oś obrotu kuli. Przekrój osiowy kuli jest kołem
twierdzenie dotyczące zależności między kątami, bokami w trójkącie i promieniem okręgu opisanego na trójkącie
twierdzenie określające związek między kątem i bokami w trójkącie