W ostrosłupie prawidłowym czworokątnym krawędź podstawy jest dwa razy krótsza od krawędzi bocznej. Wyznacz kąt, jaki tworzy w tym ostrosłupie krawędź boczna z przekątną podstawy.

Rozwiązanie

Zaczniemy oczywiście od rysunku.

R1KMNausmEfwU

Ilustracja przedstawia ostrosłup o podstawie czworokąta. Wierzchołki podstawy to A B C D , a wierzchołek ostrosłupa podpisano literą W. Krawędź podstawy podpisano literą a. Krawędź ściany bocznej podpisano literą 2a. W ostrosłupie zaznaczono jego wysokość, a spodek wysokości podpisano literą S. W podstawie zaznaczono jej przekątne. Pomiędzy wysokością a jedną z przekątnych zaznaczono kąt prosty. Pomiędzy krawędzią boczną WB a przekątną AC zaznaczono kąt i podpisano go literą alfa.

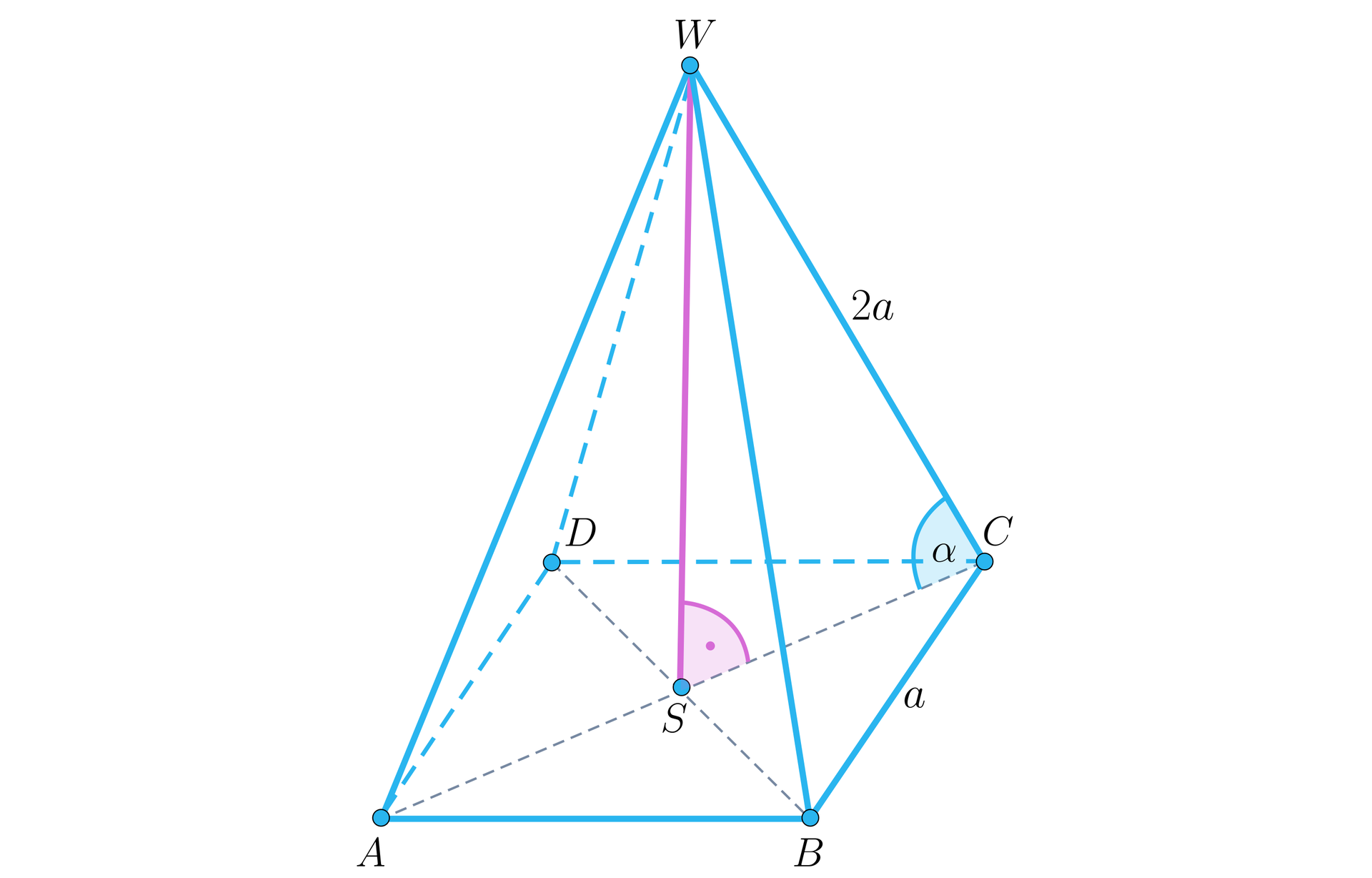
Aby wyznaczyć miarę kąta między krawędzią boczną ostrosłupa a przekątną jego podstawy wystarczy określić, w jakim pozostają one ze sobą stosunku. Oczywiście jeśli przyjmiemy, że krawędź podstawy ma długość $a$, to jej przekątna ma długość $a\sqrt{2}$. Krawędź boczna ostrosłupa, to na podstawie tekstu zadania, odcinek długości $2a$. Ostatecznie, korzystając z funkcji trygonometrycznych dla trójkąta $CSW$ otrzymamy:

$\frac{\left|CS\right|}{\left|CW\right|}=\cos \alpha$

$\frac{\frac{a\sqrt{2}}{2}}{2a}=\cos \alpha$

$\frac{\sqrt{2}}{4}=\cos \alpha$

$0,3536\approx \cos \alpha$

Wykorzystując tablice matematyczne możemy podać już miarę kąta, o który pytają w zadaniu: $\left|\sphericalangle SCW\right|\approx {69}^{\circ }$. Odpowiedź jest przybliżona ze względu na wykorzystanie tablic trygonometrycznych. Dlatego często traktuje się samo wyznaczenie funkcji trygonometrycznej danego kąta ostrego, jako jednoznaczne określenie miary tego kąta i ostateczną odpowiedź do zadania.

Podstawą ostrosłupa jest trójkąt równoboczny o boku długości $20 \mathrm{cm}$. Jego jedna ściana boczna, prostopadła do podstawy, jest trójkątem przystającym do podstawy. Oblicz miarę kąta, jaki tworzy najdłuższa krawędź tego ostrosłupa z jego krawędzią podstawy.

Rozwiązanie.

Zacznijmy od analizy własności naszej bryły.

RBJfOtnTRHRdu

Ilustracja przedstawia ostrosłup, którego podstawą jest trójkąt równoboczny. Wierzchołki podstawy to A B C, wierzchołek górny ostrosłupa podpisano liter D. Wysokość ostrosłupa DS jest jednocześnie wysokością ściany bocznej A C D. Wysokość DS. została połączona z wysokością podstawy BS. Pomiędzy tymi wysokościami zaznaczono kat prosty.

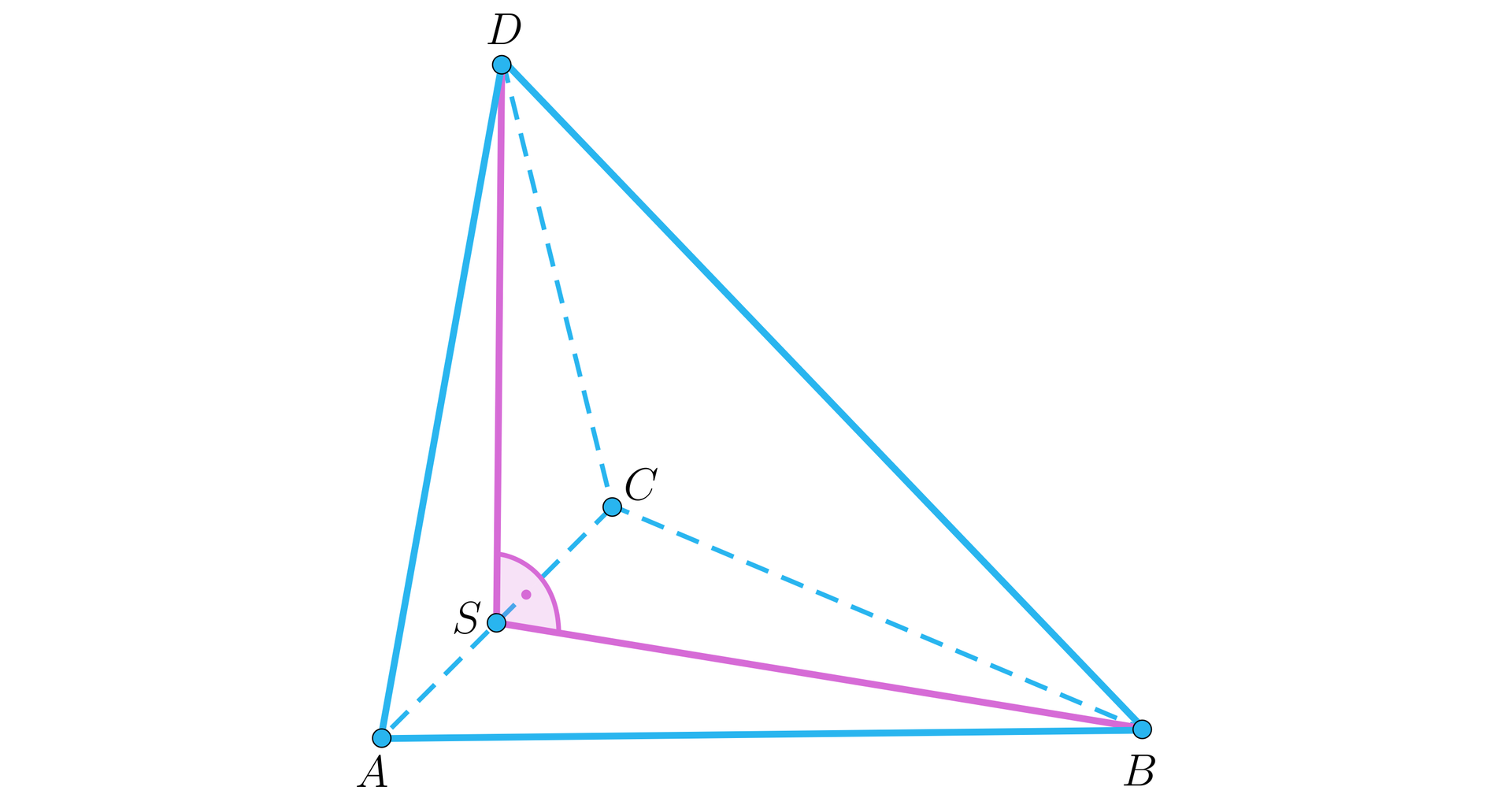
W przypadku czworościanu, w którym dwie ściany są trójkątami równobocznymi i przystającymi (u nas $\mathrm{\Delta }ABC$ oraz $\mathrm{\Delta }ACD$), jedynie jedna krawędź jest krawędzią istotnie różnej długości. Zaczniemy zatem od obliczenia długości krawędzi $BD$ naszego ostrosłupa. Zauważmy, że trójkąt $DSB$ jest trójkątem prostokątnym i równoramiennym. Jego przyprostokątne, to wysokości $h$ przystających trójkątnych ścian równobocznych ostrosłupa.

Zatem ostatecznie, korzystając z trójkąta $DSB$ mamy: $\left|DB\right|=h\sqrt{2}=\frac{20\sqrt{3}}{2}\sqrt{2}=10\sqrt{6}$.

Aby wyznaczyć miarę kąta między krawędzią $DB$ ostrosłupa a jego krawędzią podstawy, wykorzystamy twierdzenie cosinusówtwierdzenie cosinusówtwierdzenie cosinusów w trójkącie $DAB$.

${20}^2={20}^2+{\left(10\sqrt{6}\right)}^2-2·20·10\sqrt{6}·\cos \sphericalangle DBA$

$400=400+600-400\sqrt{6}\cos \sphericalangle DBA$

$400\sqrt{6}\cos \sphericalangle DBA=600$

$\cos \sphericalangle DBA=\frac{\sqrt{6}}{4}$

Jeżeli chcemy podać przybliżoną miarę w stopniach tego kąta, musimy zaokrąglić otrzymany wynik otrzymując $\cos \sphericalangle DBA\approx 0,6124$ i odczytać z tablic matematycznych miarę kąta otrzymując w przybliżeniu wynik $52°$.

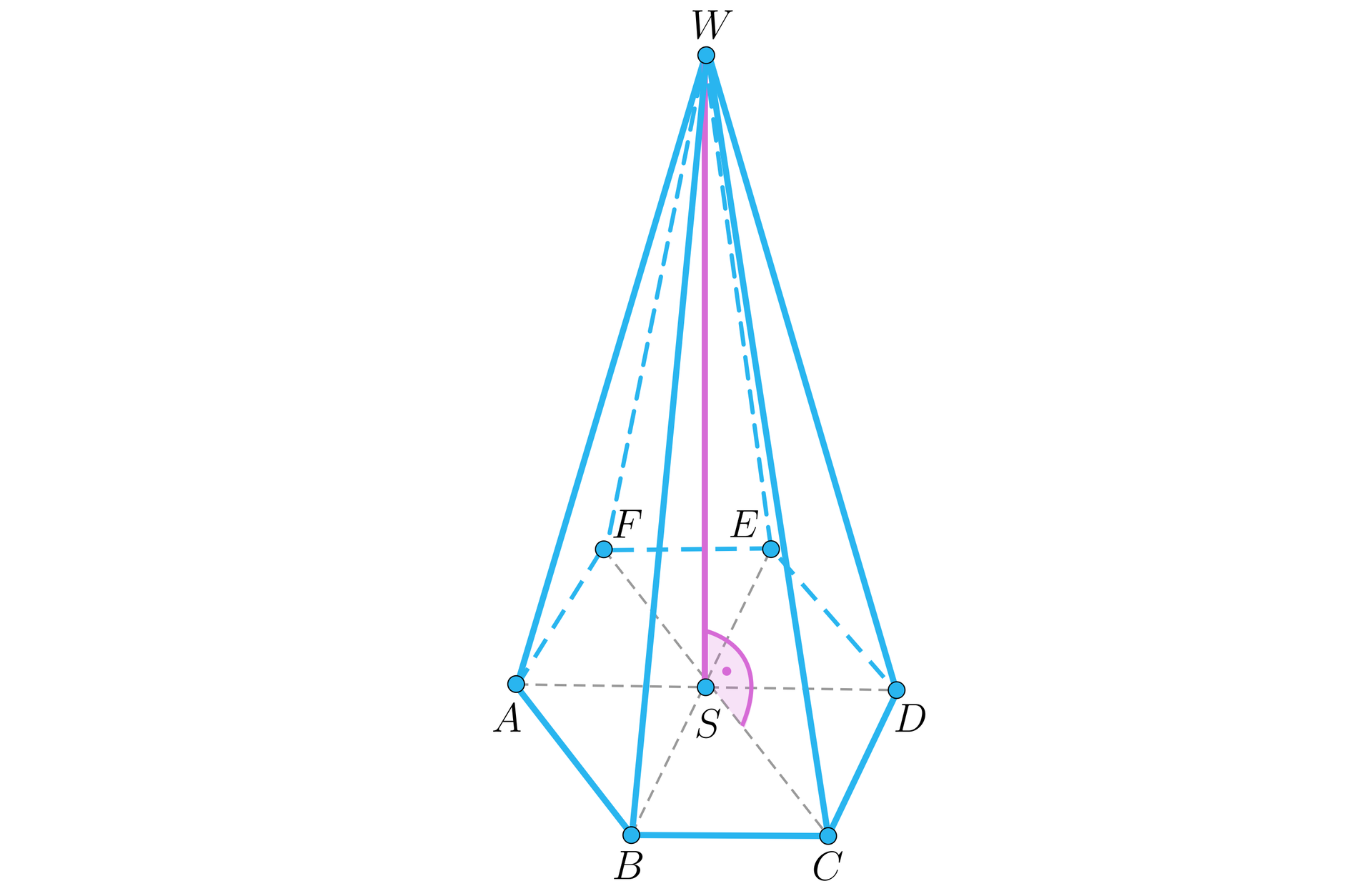
Dany jest ostrosłup prawidłowy sześciokątny, w którym krawędź podstawy ma długość $12 \mathrm{cm}$. Stosunek długości krawędzi podstawy do długości wysokości ostrosłupa jest równy $3:4$. Oblicz sinus kąta między sąsiednimi krawędziami bocznymi tego ostrosłupa.

Rozwiązanie.

Zacznijmy od rysunku:

R1bDSxDvvnazy

Ilustracja przedstawia ostrosłup o podstawie sześciokąta. Wierzchołki podstawy to A B C D E F , a wierzchołek ostrosłupa podpisano literą W. W ostrosłupie zaznaczono jego wysokość i podpisano ją literą H, a spodek wysokości podpisano literą S. W podstawie zaznaczono jej wszystkie przekątne. Pomiędzy wysokością a przekątną FC zaznaczono kąt prosty. W ostrosłupie zaznaczono kąt pomiędzy krawędziami bocznymi AW i BW.

Skoro ostrosłup jest prawidłowyostrosłup prawidłowyostrosłup jest prawidłowy, to jego podstawą jest sześciokąt foremny zbudowany z sześciu przystających trójkątów równobocznych o boku długości $12 \mathrm{cm}$. Skoro stosumek długości krawędzi podstawy do wysokości wynosi $3:4$, to wysokość ostrosłupa ma długość $16$. Korzystając z trójkąta $WSA$ obliczymy krawędź boczną ostrosłupa:

${\left|WA\right|}^2={\left|WS\right|}^2+{\left|AS\right|}^2$

${\left|WA\right|}^2={12}^2+{16}^2$

${\left|WA\right|}^2=144+256$

${\left|WA\right|}^2=400$

$\left|WA\right|=20$

Mając długość krawędzi ściany bocznej, możemy obliczyć sinus kąta między krawędziami bocznymi ostrosłupa. Wykorzystamy w tym celu metodę porównywania pól. Po pierwsze, korzystając ze wzoru Herona,wzór Heronawzoru Herona, obliczymy pole ściany bocznej ostrosłupa.

$P=\sqrt{26·6·6·14}=12\sqrt{91}$

następnie wykorzystamy wzór na pole trójkąta używający funkcji trygonometrycznej sinus

$P=\frac{1}{2}ab\sin \alpha$.

Mamy zatem:

$12\sqrt{91}=\frac{1}{2}·20·20·\sin \sphericalangle AWB$

$12\sqrt{91}=200·\sin \sphericalangle AWB$

$\frac{3\sqrt{91}}{25}=\sin \sphericalangle AWB$

Na koniec pokażemy jeszcze przykład, w którym wykorzystamy jednocześnie kilka opisanych we wstępie metod znanych z planimetrii pozwalających wyznaczyć miary kątów.

Podstawą ostrosłupa $ABCW$ jest trójkąt równoramienny o ramionach $AB$ i $AC$ długości $10 \mathrm{cm}$ oraz podstawie $BC$ długości $16 \mathrm{cm}$. Wszystkie krawędzie boczne tego ostrosłupa są równe $10 \mathrm{cm}$. Oblicz miary kątów, jakie tworzą te krawędzie boczne z wysokością ostrosłupa opuszczoną z wierzchołka $W$.

Rozwiązanie.

Zauważmy, że w zadaniu przekazana jest informacja, że dany ostrosłup jest prostyostrosłup prostyostrosłup jest prosty, bo wszystkie jego krawędzie boczne są równej długości. Ponadto łatwo sprawdzić, że trójkąt podstawy jest trójkątem rozwartokątnym. Istotnie, wykorzystując twierdzenie cosinusówtwierdzenie cosinusówtwierdzenie cosinusów mamy:

${16}^2={10}^2+{10}^2-2·10·10·\cos \sphericalangle BAC$

$256=200-200\cos \sphericalangle BAC$

$\cos \sphericalangle BAC=-\frac{56}{200}$

$\cos \sphericalangle BAC=-\frac{7}{25}$.

Jeżeli cosinus kąta wewnętrznego trójkąta jest ujemny, to jest to kąt rozwarty. Ostatecznie spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie i konsekwentnie jest punktem leżącym na zewnątrz trójkąta $ABC$. Wykonujemy odpowiedni szkic do zadania:

Rwpz9BZoE0H3L

Ilustracja przedstawia ostrosłup, którego podstawą jest trójkąt równoramienny. Wierzchołki podstawy to A B C, wierzchołek górny ostrosłupa podpisano literą W. Podstawa ostrosłupa została wpisana w okrąg, a spodek wysokości oznaczony literą S jest środkiem tego okręgu. Kąt pomiędzy wysokością WS a odcinkiem AS jest kątem prostym. Odcinek AS podpisano literą R. W ostrosłupie zaznaczono kąt pomiędzy krawędzią boczną AW i wysokością ostrosłupa SW, kąt ten podpisano literą alfa.

Promień okręgu opisanego na podstawie ostrosłupa możemy obliczyć korzystając z twierdzenia sinusówtwierdzenie sinusówtwierdzenia sinusów dla trójkąta $ABC$.

$\frac{\left|BC\right|}{\sin \sphericalangle BAC}=2R$

$\frac{16}{\sqrt{1-{\left(-\frac{7}{25}\right)}^2}}=2R$

$\frac{16}{\sqrt{1-\frac{49}{625}}}=2R$

$\frac{16}{\sqrt{\frac{576}{625}}}=2R$

$\frac{400}{24}=2R$

$\frac{50}{3}=2R$

$\frac{25}{3}=R$

W ostatnim etapie zadania wykorzystamy definicje funkcji trygonometrycznych dla trójkątów prostokątnych, których dwoma przyprostokątnymi są odpowiednio: wysokość ostrosłupa i promień okręgu opisanego na podstawie, zaś przeciwprostokątną jest krawędź boczna ostrosłupa. Z trójkąta $ASW$ mamy:

$\frac{R}{\left|WA\right|}=\sin \sphericalangle AWS$

$\frac{25}{30}=\sin \sphericalangle AWS$

$\frac{5}{6}=\sin \sphericalangle AWS$

$0,8333\approx \sin \sphericalangle AWS$

Z tablic matematycznych możemy zatem odczytać, że kąt miedzy wysokością ostrosłupa a jego krawędzią boczną $AW$ ma miarę około $56°$.

Analogicznie postępując dla kolejnych dwóch krawędzi bocznych naszego ostrosłupa, otrzymamy dokładnie takie same równości. Wynika to oczywiście z faktu, że nasz ostrosłup jest prosty. Warto zatem zapamiętać, że w ostrosłupach prostych kąt między wysokością ostrosłupa a jego krawędziami bocznymi jest kątem stałej miary.

twierdzenie pozwalające ustalić związek między bokami i kątami trójkąta oraz promieniem okręgu na nim opisanego.

W dowolnym trójkącie stosunek długości jego boku do sinusa kąta leżącego na przeciw jest stały i równy średnicy okręgu opisanego na tym trójkącie

twierdzenie określające związek między kątem wewnętrznym trójkąta i bokami tego trójkąta.

W dowolnym trójkącie kwadrat długości jednego z boków jest równy sumie kwadratów długości pozostałych dwóch boków pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta między nimi zawartego

ostrosłupem prawidłowym nazywamy taki ostrosłup prosty, którego podstawa jest wielokątem foremnym

ostrosłupem prostym nazywamy taki ostrosłup, którego wszystkie krawędzie boczne są tej samej długości

wzór pozwalający obliczyć pole dowolnego trójkąta, jeżeli znamy długości wszystkich boków tego trójkąta

Jeżeli boki trójkąta są odpowiednio równe $a$, $b$, $c$, a przez $p$ oznaczymy połowę obwodu tego trójkąta, to pole tego trójkąta jest równe $P=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$