Przeczytaj

Wzór dwumianowy

Wzór dwumianowy, zwany też wzorem dwumiennym, wzorem Newtona lub dwumianem Newtonadwumian Newtonadwumianem Newtona to nazwa twierdzenia, zgodnie z którym potęgę dwumianu ${(a + b)}^{n}$ można rozwinąć w sumę jednomianów, przy których współczynniki liczbowe są odpowiednimi symbolami Newtona. Współczynniki te zwane są współczynnikami dwumianowymi.

Przypomnijmy zatem najpierw, jak wyznaczamy symbol Newtona $(\begin{array}{l} n \\ k \end{array})$ , który pojawi się we wzorze dwumiennym Newtona jako współczynnik przy $k$ –tym wyrazie rozwinięcia dwumianu.

$(\begin{array}{l} n \\ k \end{array}) = \frac{n!}{k! \cdot (n - k)!}$ dla $0 \leq k \leq n$ i $n \in ℕ$ , $k \in ℕ$

Symbol $(\begin{array}{l} n \\ k \end{array})$ odczytujemy jako $n$ nad $k$ lub $n$ po $k$ .

Dwumian Newtona

Twierdzenie: Dwumian Newtona

Jeśli $a$ , $b$ są dowolnymi liczbami rzeczywistymi i $n$ jest liczbą naturalną dodatnią to:

{(a + b)}^{n} = (\begin{array}{l} n \\ 0 \end{array}) a^{n} + (\begin{array}{l} n \\ 1 \end{array}) a^{n - 1} b + (\begin{matrix} n \\ 2 \end{matrix}) a^{n - 2} b^{2} + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) a b^{n - 1} + (\begin{matrix} n \\ n \end{matrix}) b^{n}

Przykład 1

Zapiszemy rozwinięcie trzeciej potęgi sumy $a + b$ , korzystając z dwumianu Newtona.

${(a + b)}^{3} = (\begin{array}{l} 3 \\ 0 \end{array}) a^{3} + (\begin{array}{l} 3 \\ 1 \end{array}) a^{3 - 1} b^{1} + (\begin{array}{l} 3 \\ 2 \end{array}) a^{3 - 2} b^{2} + (\begin{array}{l} 3 \\ 3 \end{array}) a^{3 - 3} b^{3}$

Obliczymy kolejne współczynniki liczbowe rozwinięcia.

$(\begin{array}{l} 3 \\ 0 \end{array}) = 1$

$(\begin{array}{l} 3 \\ 1 \end{array}) = 3$

$(\begin{array}{l} 3 \\ 3 \end{array}) = 1$

$(\begin{array}{l} 3 \\ 2 \end{array}) = \frac{3!}{2! \cdot (3 - 2)!} = \frac{3}{1} = 3$

Podstawiamy wyznaczone liczby do uzyskanego rozwinięcia.

${(a + b)}^{3} = 1 \cdot a^{3} + 3 \cdot a^{2} b^{1} + 3 \cdot a^{1} b^{2} + 1 \cdot b^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

Przykład 2

Zapiszemy w postaci sumy jednomianów potęgę ${(x^{2} - 2 y)}^{5}$ , korzystając z dwumianu Newtona.

${(x^{2} - 2 y)}^{5} = (\begin{array}{l} 5 \\ 0 \end{array}) {(x^{2})}^{5} + (\begin{matrix} 5 \\ 1 \end{matrix}) {(x^{2})}^{4} \cdot (- 2 y) + (\begin{array}{l} 5 \\ 2 \end{array}) {(x^{2})}^{3} \cdot {(- 2 y)}^{2} +$

$+ (\begin{array}{l} 5 \\ 3 \end{array}) {(x^{2})}^{2} \cdot {(- 2 y)}^{3} + (\begin{array}{l} 5 \\ 4 \end{array}) {(x^{2})}^{1} \cdot {(- 2 y)}^{4} + (\begin{array}{l} 5 \\ 5 \end{array}) \cdot {(- 2 y)}^{5}$

Obliczamy wartości kolejnych współczynników liczbowych.

$(\begin{array}{l} 5 \\ 0 \end{array}) = 1$

$(\begin{array}{l} 5 \\ 1 \end{array}) = 5$

$(\begin{array}{l} 5 \\ 2 \end{array}) = \frac{5!}{2! \cdot (5 - 2)!} = \frac{5 \cdot 4 \cdot 3}{3!} = \frac{60}{6} = 10$

$(\begin{array}{l} 5 \\ 3 \end{array}) = \frac{5!}{3! \cdot (5 - 3)!} = \frac{5 \cdot 4}{2!} = \frac{20}{2} = 10$

$(\begin{array}{l} 5 \\ 4 \end{array}) = \frac{5!}{4! \cdot (5 - 4)!} = \frac{5}{1!} = \frac{5}{1} = 5$

$(\begin{array}{l} 5 \\ 5 \end{array}) = \frac{5!}{5! \cdot (5 - 5)!} = \frac{1}{0!} = 1$

Podstawiamy znalezione liczby do uzyskanego rozwinięcia i wykonujemy potęgowanie.

${(x^{2} - 2 y)}^{5} = 1 \cdot x^{10} + 5 \cdot x^{8} \cdot (- 2 y) + 10 x^{6} \cdot 4 y^{2} +$

$+ 10 \cdot x^{4} \cdot (- 8 y^{3}) + 5 \cdot x^{2} \cdot 16 y^{4} + 1 \cdot (- 32 y^{5})$

Wykonujemy mnożenie.

${(x^{2} - 2 y)}^{5} = x^{10} - 10 \cdot x^{8} y + 40 x^{6} y^{2} - 80 x^{4} y^{3} + 80 x^{2} y^{4} - 32 y^{5}$

Jeśli we wzorze na dwumian Newtonadwumian Newtonadwumian Newtona podstawimy $a = 1$ , $b = x$ to otrzymamy wzór na tak zwany szereg Newtona.

Ważne!

Wzór na szereg Newtona

{(1 + x)}^{n} = (\begin{array}{l} n \\ 0 \end{array}) + (\begin{array}{l} n \\ 1 \end{array}) x + (\begin{array}{l} n \\ 2 \end{array}) x^{2} + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) x^{n - 1} + (\begin{array}{l} n \\ n \end{array}) x^{n}

Przykład 3

Obliczymy sumę współczynników liczbowych w szeregu Newtona.

Podstawiamy do wzoru na szereg Newtona $x = 1$ .

${(1 + 1)}^{n} = (\begin{array}{l} n \\ 0 \end{array}) + (\begin{array}{l} n \\ 1 \end{array}) + (\begin{array}{l} n \\ 2 \end{array}) + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) + (\begin{array}{l} n \\ n \end{array})$

$2^{n} = (\begin{array}{l} n \\ 0 \end{array}) + (\begin{array}{l} n \\ 1 \end{array}) + (\begin{array}{l} n \\ 2 \end{array}) + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) + (\begin{array}{l} n \\ n \end{array})$

Odpowiedź:

Suma współczynników liczbowych rozwinięcia $n$ –tej potęgi sumy $1 + x$ jest równa $2^{n}$ .

Do wzoru na szereg Newtona podstawiamy teraz $x = - 1$ .

$0 = (\begin{array}{l} n \\ 0 \end{array}) - (\begin{array}{l} n \\ 1 \end{array}) + (\begin{array}{l} n \\ 2 \end{array}) - (\begin{array}{l} n \\ 3 \end{array}) + \dots + {(- 1)}^{n} \cdot (\begin{array}{l} n \\ n \end{array})$

Stąd otrzymujemy:

$(\begin{array}{l} n \\ 0 \end{array}) + (\begin{array}{l} n \\ 2 \end{array}) + (\begin{array}{l} n \\ 4 \end{array}) + . . . = (\begin{array}{l} n \\ 1 \end{array}) + (\begin{array}{l} n \\ 3 \end{array}) + (\begin{array}{l} n \\ 5 \end{array}) + \dots$

Wnioskujemy więc, że w rozwinięciu potęgi ${(1 + x)}^{n}$ suma współczynników potęg o wykładnikach parzystych jest równa sumie współczynników potęg o wykładnikach nieparzystych. Każda z tych sum jest równa $2^{n - 1}$ .

Przykład 4

Jeśli $n = 6$ to

$(\begin{array}{l} 6 \\ 0 \end{array}) + (\begin{array}{l} 6 \\ 2 \end{array}) + (\begin{array}{l} 6 \\ 4 \end{array}) + (\begin{array}{l} 6 \\ 6 \end{array}) = (\begin{array}{l} 6 \\ 1 \end{array}) + (\begin{array}{l} 6 \\ 3 \end{array}) + (\begin{array}{l} 6 \\ 5 \end{array}) = 2^{5}$

Jeśli $n = 7$ to

$(\begin{array}{l} 7 \\ 0 \end{array}) + (\begin{array}{l} 7 \\ 2 \end{array}) + (\begin{array}{l} 7 \\ 4 \end{array}) + (\begin{array}{l} 7 \\ 6 \end{array}) = (\begin{array}{l} 7 \\ 1 \end{array}) + (\begin{array}{l} 7 \\ 3 \end{array}) + (\begin{array}{l} 7 \\ 5 \end{array}) + (\begin{array}{l} 7 \\ 7 \end{array}) = 2^{6}$

Dwumian Newtona a trójkąt Pascala

Porównując liczby w kolejnych wierszach trójkąta Pascala i kolejne współczynniki liczbowe w szeregu Newtona, zauważamy, że liczby te są równe.

Wartości kolejnych symboli Newtona można zapisać w postaci trójkąta Pascala.

Rs87jozD0P5KM

Ilustracja przedstawia zestaw liczb w postaci dwóch trójkątów, składających się z sześciu wierszy, opisanych od zera do pięć. Trójkąt po lewej stronie: od góry, wiersz zero: jeden; wiersz pierwszy: jeden, jeden; wiersz drugi: jeden, dwa, jeden; wiersz trzeci: jeden, trzy, trzy, jeden; wiersz czwarty: jeden, cztery, sześć, cztery, jeden; wiersz piąty: jeden, pięć, dziesięć, dziesięć, pięć, jeden. Trójkąt po prawej stronie pokazuje liczby w formie symboli Newtona. Wiersz zero: zero nad zero, wiersz pierwszy: jeden nad zero, jeden nad jeden; wiersz drugi: dwa nad zero, dwa nad jeden, dwa nad dwa; wiersz trzeci: trzy nad zero, trzy nad jeden, trzy nad dwa, trzy nad trzy; wiersz czwarty: cztery nad zero, cztery nad jeden, cztery nad dwa, cztery nad trzy, cztery nad cztery; wiersz piąty: pięć nad zero, pięć nad jeden, pięć nad dwa, pięć nad trzy, pięć nad cztery, pięć nad pięć.

Kolejnym wierszom trójkąta odpowiadają kolejne wartości $n$ , kolejnym wyrazom w każdym wierszu – kolejne wartości $k$ .

Skrajne wyrazy w każdym wierszu równe są jedności, każdy wyraz (poza skrajnymi) jest sumą dwu wyrazów stojących bezpośrednio nad nim.

Korzystając z trójkątnej tablicy, można więc szybko znaleźć potrzebne współczynniki przy danej potędze dwumianu.

RwsNVqBip30YA

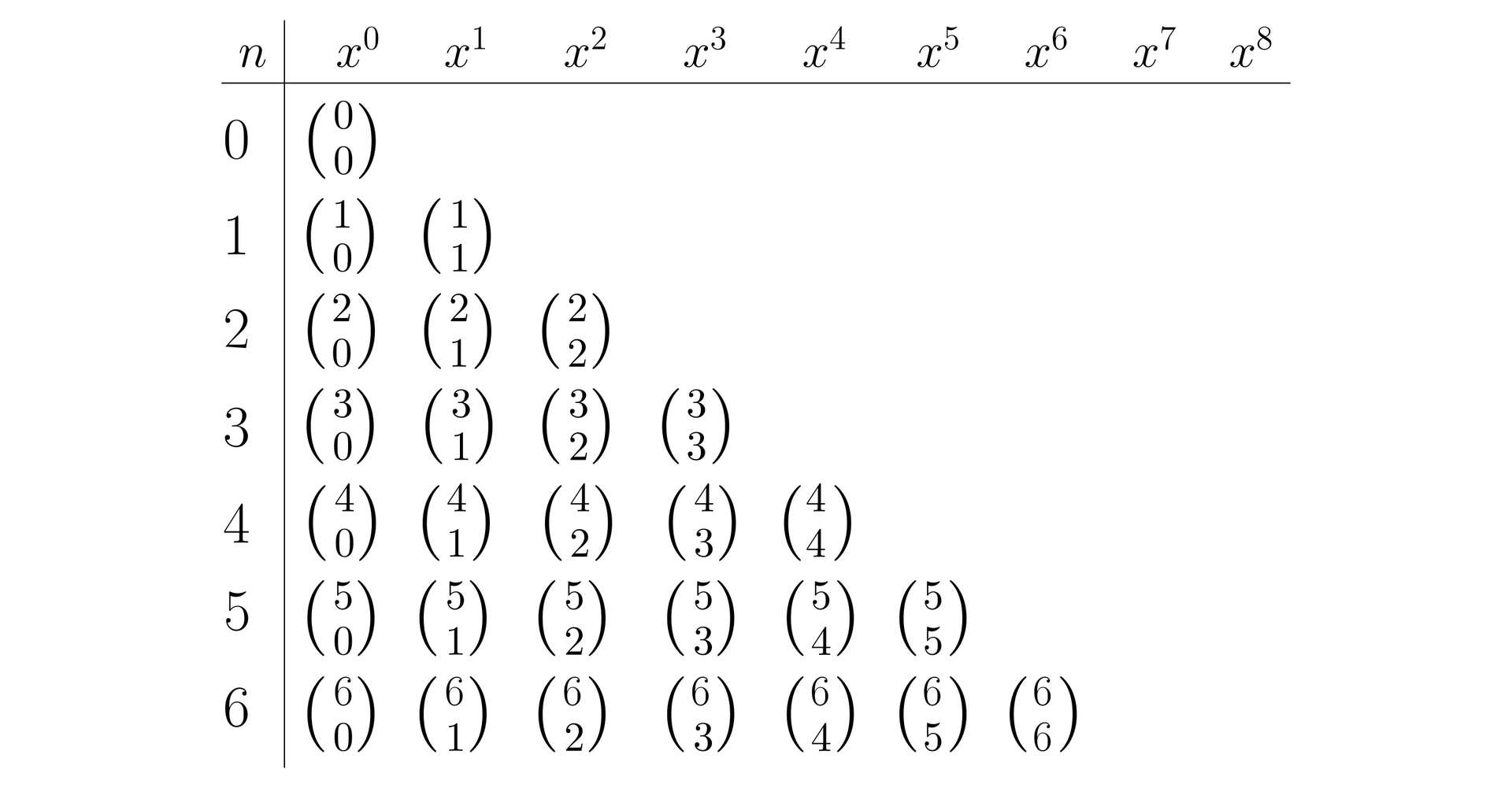
Ilustracja przedstawia tabelę. Kolejne kolumny tabeli zostały opisane w następujący sposób, pierwsza jest podpisana literą n, druga x do potęgi zerowej , trzecia x do potęgi pierwszej, i tak dalej aż do wartości x do potęgi ósmej. Zatem mamy 10 kolumn. W pierwszej kolumnie, podpisanej literą n, znajdują się wartości od zera do sześciu. Zatem łącznie nasza tabela składa się z 6 wierszy. W drugiej kolumnie podpisanej x0 znajduje się 6 symboli newtona od : zero nad zero, jeden nad zero, dwa nad zero, trzy nad zero, cztery nad zero, pięć nad zero, sześć nad zero. W trzeciej kolumnie podpisanej x1 pierwszy wiersz jest pusty, zaczynając od drugiego wiersza mamy następujące symbole newtona: jeden nad jeden, dwa nad jeden, trzy nad jeden, cztery nad jeden, pięć nad jeden, sześć nad jeden. W czwartej kolumnie podpisanej x2, symbole zaczynają się dopiero w trzecim wierszu na wysokości cyfry dwa i są to kolejno: dwa nad dwa, trzy nad dwa, cztery nad dwa, pięć nad dwa, sześć nad dwa. W kolejnej kolumnie zaczynamy od czwartego wiersza i mamy: trzy nad trzy, cztery nad trzy, pięć nad trzy, sześć nad trzy. W szóstej kolumnie, zaczynamy od piątego wiersza i mamy: cztery nad cztery, pięć nad cztery, sześć nad cztery. W kolejnej kolumnie mamy już tylko dwa wyrażenia pięć nad pięć i sześć nad sześć, a w ostatniej kolumnie- ósmej, która jest podpisana x6, w ostatnim- szóstym wierszu mamy jeden symbol newtona sześć nad sześć.

Przykład 5

Określimy współczynnik liczbowy przy $4$ wyrazie piątej potęgi sumy $x + 1$ .

Z powyższej tabeli odczytujemy, że czwarty współczynnik liczbowy to $(\begin{array}{l} 5 \\ 3 \end{array})$ .

Sprawdzamy w trójkącie Pascala, że odpowiada on liczbie $10$ . Zatem szukany współczynnik jest równy $10$ .

Wiemy już, że sumy liczb w kolejnych wierszach trójkąta Pascala są równe kolejnym potęgom liczby $2$ . Własność tę możemy wykorzystać, chcąc szybko obliczyć sumę symboli Newtona występujących w kolejnych potęgach dwumianu.

Na przykład:

(\begin{array}{l} 2 \\ 0 \end{array}) + (\begin{array}{l} 2 \\ 1 \end{array}) + (\begin{array}{l} 2 \\ 2 \end{array}) = 2^{2}

(\begin{array}{l} 3 \\ 0 \end{array}) + (\begin{array}{l} 3 \\ 1 \end{array}) + (\begin{array}{l} 3 \\ 2 \end{array}) + (\begin{array}{l} 3 \\ 3 \end{array}) = 2^{3}

(\begin{array}{l} 4 \\ 0 \end{array}) + (\begin{array}{l} 4 \\ 1 \end{array}) + (\begin{array}{l} 4 \\ 2 \end{array}) + (\begin{array}{l} 4 \\ 3 \end{array}) + (\begin{array}{l} 4 \\ 4 \end{array}) = 2^{4}

Zwróć uwagę, że obliczając sumę symboli Newtona w kolejnych potęgach sumy $1 + x$ , można postąpić dwoma sposobami: skorzystać z własności podanej w Przykładzie 3 lub sumy liczb w wierszach trójkąta Pascala.

Wzór na $k$ –ty wyraz dwumianu Newtona

Jeśli $a$ , $b$ są dowolnymi liczbami rzeczywistymi, $n$ jest liczbą naturalną dodatnią, $k$ jest liczbą naturalną taką, że $0 \leq k \leq n$ to, $k$ –ty wyraz rozwinięcia potęgi ${(a + b)}^{n}$ wyraża się wzorem:

(\begin{matrix} n \\ k - 1 \end{matrix}) \cdot (a^{n + 1 - k} b^{k - 1})

Korzystając z tego wzoru, można wyznaczyć dowolny wyraz dwumianu Newtona.

Przykład 6

Znajdziemy szósty wyraz $w_{6}$ rozwinięcia potęgi ${(3 x + 2)}^{8}$ .

Do wzoru $(\begin{matrix} n \\ k - 1 \end{matrix}) \cdot (a^{n + 1 - k} b^{k - 1})$ podstawiamy: $n = 8$ , $k = 6$ .

$w_{6} = (\begin{matrix} 8 \\ 6 - 1 \end{matrix}) \cdot {(3 x)}^{8 + 1 - 6} \cdot 2^{6 - 1}$

$w_{6} = (\begin{array}{l} 8 \\ 5 \end{array}) \cdot {(3 x)}^{3} \cdot 2^{5}$

$w_{6} = \frac{8!}{5! \cdot 3!} \cdot 27 x^{3} \cdot 32$

$w_{6} = \frac{8 \cdot 7 \cdot 6}{6} \cdot 864 x^{3} = 48384 x^{3}$

Odpowiedź:

Szósty wyraz rozwinięcia potęgi ${(3 x + 2)}^{8}$ jest równy $48384 x^{3}$ .

Słownik

dwumian Newtona

to twierdzenie: jeśli $a$ , $b$ są dowolnymi liczbami rzeczywistymi i $n$ jest liczbą naturalną dodatnią to

{(a + b)}^{n} = (\begin{array}{l} n \\ 0 \end{array}) a^{n} + (\begin{array}{l} n \\ 1 \end{array}) a^{n - 1} b + (\begin{matrix} n \\ 2 \end{matrix}) a^{n - 2} b^{2} + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) a b^{n - 1} + (\begin{matrix} n \\ n \end{matrix}) b^{n}

Wprowadzenie

Animacja

Wzór dwumianowy

Dwumian Newtona a trójkąt Pascala

Wzór na $k$ –ty wyraz dwumianu Newtona

Słownik

Wprowadzenie

Animacja

Przeczytaj

Wzór dwumianowy

Dwumian Newtona a trójkąt Pascala

Wzór na k–ty wyraz dwumianu Newtona

Słownik

Wzór na $k$ –ty wyraz dwumianu Newtona