W ostrosłupie prawidłowym trójkątnym o długości krawędzi podstawy $a$ oraz długości krawędzi bocznej $b$ wyznaczymy kąt pomiędzy ścianą boczną a płaszczyzną podstawy.

Rozwiązanie

Przyjmijmy oznaczenia takie jak na rysunku.

R1AdpxkKFkXcL

Na ilustracji przedstawiono ostrosłup prawidłowy trójkątny. Długość krawędzi podstawy oznaczono literą a, natomiast długość krawędzi bocznej oznaczono literą b. Z wierzchołka A opuszczono wysokość trójkąta, znajdującego się w podstawie, której spodek znajduje się w punkcie E na boku $BC$. Z wierzchołka D opuszczono wysokość ostrosłupa, której spodek leży w punkcie F na wysokości $AE$ podstawy. Z wierzchołka D opuszczono również wysokość ściany bocznej do punktu E i oznaczono ją $h_1$. Długość odcinka $FE$ wynosi $\frac{1}{3}{h}_2$. $\angle DEF$ oznaczono alfa.

W celu wyznaczenia kąta pomiędzy ścianą boczną a podstawą obieramy punkt $E$ będący środkiem krawędzi $BC$. Zauważmy, że odcinki $DE$ i $AE$ są wysokościami trójkątów $CBD$ i $CBA$, ponieważ pierwszy trójkąt jest równoramienny a drugi równoboczny wiec spodki obu wysokości dzielą odcinek $BC$ na pół w punkcie $E$. Wysokości te są oczywiście prostopadłe do krawędzi $BC$.

Z trójkąta prostokątnego $BED$ wyznaczamy długość wysokości $DE$:

$h_1=\sqrt{b^2-{\left(\frac{a}{2}\right)}^2}=\frac{1}{2}\sqrt{4b^2-a^2}$.

Ponieważ $a<\sqrt{3}b$, więc $4b^2-a^2>0$.

Wysokość trójkąta równobocznego $ABC$ ma długość $h_2=\frac{a\sqrt{3}}{2}$. Ponadto $\left|EF\right|=\frac{1}{3}{h}_2=\frac{a\sqrt{3}}{6}$.

Z trójkąta prostokątnego $DFE$ wyznaczamy:

$\cos \alpha =\frac{\left|EF\right|}{\left|DE\right|}=\frac{{\displaystyle \frac{a\sqrt{3}}{6}}}{\frac{1}{2}\sqrt{4b^2-a^2}}=\frac{a\sqrt{3}}{3\sqrt{4b^2-a^2}}$.

Znając długości odcinków $a$ i $b$ możemy wyznaczyć miarę kąta $\alpha$.

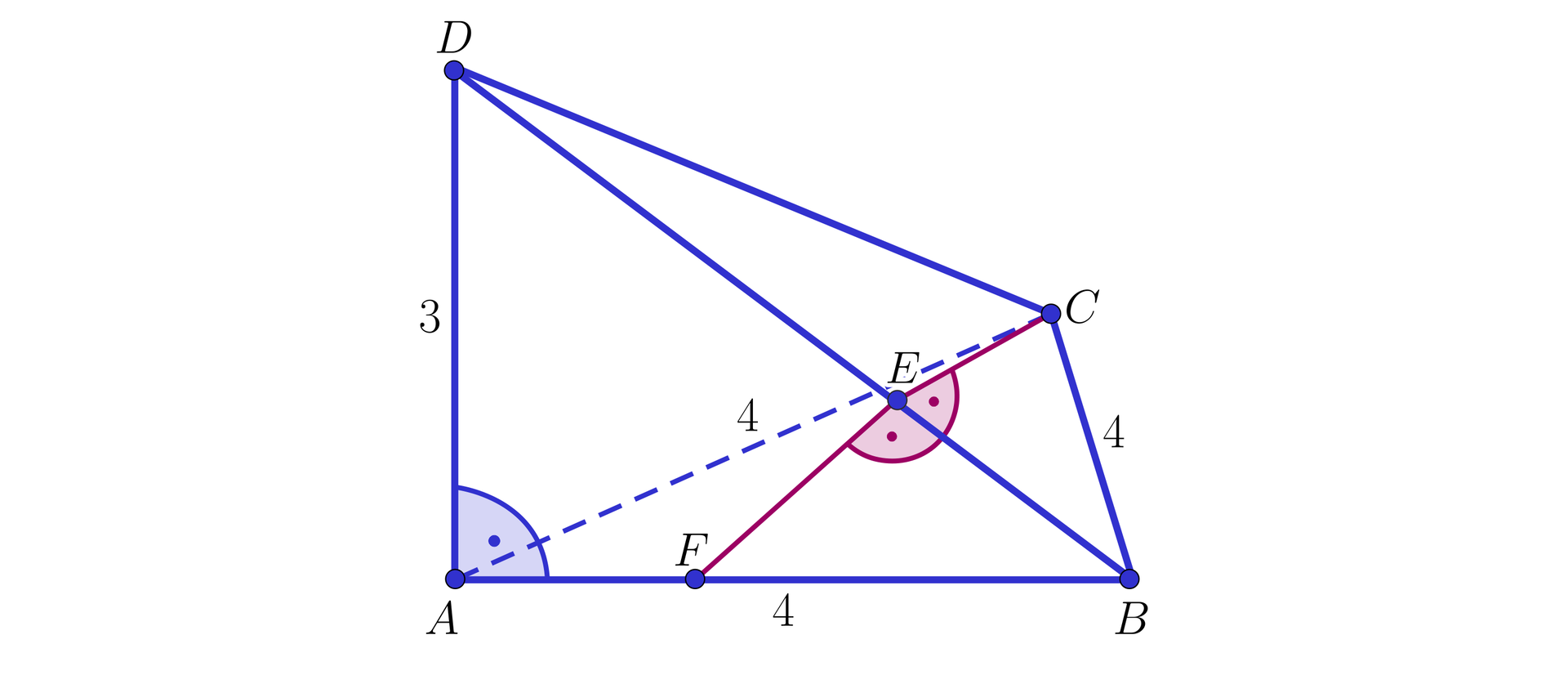
W ostrosłupie prawidłowym trójkątnym o długości krawędzi podstawy $a$ oraz długości krawędzi bocznej $b$ wyznaczymy kąt pomiędzy ścianami bocznymi tego ostrosłupa.

Rozwiązanie

Przyjmijmy oznaczenia takie jak na rysunku.

R19HRD3gxswaD

Na ilustracji przedstawiono ostrosłup prawidłowy trójkątny. Długość krawędzi podstawy oznaczono literą a, natomiast długość krawędzi bocznej oznaczono literą b. Z wierzchołków A i B opuszczono wysokości ścian bocznych oznaczone literą h, których spodki leżą w punkcie E na krawędzi bocznej $CD$. $\angle AEB$ oznaczono alfa.

Trójkąty $ACD$ i $BCD$ są przystające, więc wysokości prowadzone z wierzchołków $A$ i $B$ przetną się punkcie $E$ leżącym na krawędzi $CD$. Z poprzedniego przykładu wiemy, że wysokość ściany bocznej opuszczona z punktu $D$ ma długość $\frac{1}{2}\sqrt{4b^2-a^2}$. Zatem pole ściany bocznej wynosi $P=\frac{1}{4}a\sqrt{4b^2-a^2}$. Pole to jest również równe $P=\frac{1}{2}bh$, czyli

$\frac{1}{2}bh=\frac{1}{4}a\sqrt{4b^2-a^2}$,

$h=\frac{a\sqrt{4b^2-a^2}}{2b}$.

Korzystając z twierdzenia cosinusów dla trójkąta $ABE$ otrzymujemy:

$a^2=2h^2-2h^2\cos \alpha$,

$a^2=2h^2\left(1-\cos \alpha \right)$,

$a^2=\frac{a^2\left(4b^2-a^2\right)}{2b^2}\left(1-\cos \alpha \right)$,

$1-\cos \alpha =\frac{2b^2}{4b^2-a^2}$,

$\cos \alpha =1-\frac{2b^2}{4b^2-a^2}$,

$\cos \alpha =\frac{2b^2-a^2}{4b^2-a^2}$.

Znając długości odcinków $a$ i $b$ możemy wyznaczyć miarę kąta $\alpha$.

Uzasadnimy, że w ostrosłupie prawidłowym trójkątnym kąt pomiędzy ścianami bocznymi jest większy od $60°$.

Rozwiązanie

Zauważmy, że z warunku $0<a<\sqrt{3}b$ wynika, że $4b^2>4b^2-a^2>4b^2-3b^2=b^2$, więc

$\frac{1}{2}=\frac{2b^2}{4b^2}<\frac{2b^2}{4b^2-a^2}$,

Stąd cosinus kąta pomiędzy ścianami bocznymi $\cos \alpha =1-\frac{2b^2}{4b^2-a^2}<1-\frac{1}{2}=\frac{1}{2}$, więc $\alpha >60°$.

Dany jest czworościan $ABCD$, którego podstawą jest trójkąt równoboczny $ABC$ o boku długości $4$, a krawędź $AD$ o długości $3$ jest prostopadła do płaszczyzny podstawy. Wyznaczymy kąt pomiędzy ścianami $ABD$ i $BCD$.

Rozwiązanie

Sporządzamy rysunek pomocniczy:

R1LeB0lgnMxFV

Na ilustracji przedstawiono czworościan $ABCD$. Długość krawędzi podstawy wynosi 4, natomiast długość krawędzi bocznej wynosi trzy. Krawędź boczna $AD$ jest nachylona do krawędzi bocznej pod kątem prostym. Na krawędzi $Ab$ zaznaczono punkt F. Z punktu F oraz wierzchołka C poprowadzono proste prostopadłe do krawędzi bocznej $BD$ w punkcie E.

Z trójkątów prostokątnych $ABD$ i $ACD$ wyznaczamy $\left|BD\right|=\left|CD\right|=\sqrt{3^2+4^2}=5$. Zatem trójkąt $BCD$ jest trójkątem ostrokątnym.

Wspólną krawędzią ścian $ABD$ i $BCD$ jest $BD$. Zaznaczamy wysokość ściany $BCD$ opuszczoną z wierzchołka $C$. Wysokość ta przecina krawędź $BD$ w punkcie $E$. Wyznaczamy odcinek $EF$ prostopadły do krawędzi $BD$. Punkt $F$ leży na krawędzi $AB$ lub jej przedłużeniu. W celu wyznaczenia kąta dwuściennego pomiędzy ścianami $ABD$ i $BCD$ należy wyznaczyć miarę kąta płaskiego $CEF$.

Rozważmy ścianę $BCD$:

R17qlIMgweVx0

Na ilustracji przedstawiono trójkąt równoramienny $ABC$. Długość podstawy $AB$ wynosi 4, natomiast długości ramion $BD$ oraz $CD$ wynoszą pięć. Z wierzchołka C opuszczono wysokość trójkąta oznaczoną $h_1$, której spodek leży w punkcie E na boku BD. Natomiast z wierzchołka D opuszczono wysokość trójkąta oznaczoną $h_2$, której spodek znajduje się w punkcie G na podstawie $BC$. $\angle DBC$ oznaczono alfa. Odległość punktu E od wierzchołka B wynosi x.

Z trójkąta prostokątnego $BGD$ obliczamy $h_2=\sqrt{5^2-2^2}=\sqrt{21}$. Trójkąt $BEC$ jest podobny do trójkąta $BGD$ (cecha kąt‑kąt‑kąt). Zatem $\frac{h_1}{4}=\frac{h_2}{5}$, czyli $h_1=\frac{4\sqrt{21}}{5}$.

Ponadto $\frac{x}{4}=\frac{2}{5}$, czyli $x=\frac{8}{5}$.

Rozważmy ścianę $ABD$:

RavjQHuHB7os7

Na ilustracji przedstawiono trójkąt prostokątny $ABD$. Długość przyprostokątnej $AD$ wynosi 3, natomiast przyprostokątnej $AB$ wynosi cztery. $\angle ABD$ oznaczono alfa. Zaznaczono punkt F na przyprostokątnej $AB$, z którego poprowadzono prostą prostopadłą do przeciwprostokątnej w punkcie E. Zaznaczono trójkąt prostokątny $BFE$, którego przyprostokątna $FE$ ma długość z, przyprostokątna $EB$ ma długość $\frac{8}{5}$ oraz przeciwprostokątna $FB$ ma długość y.

Trójkąt $BEF$ jest podobny do trójkąta $BAD$ (cecha kąt‑kąt‑kąt). Stąd $\frac{8}{5y}=\frac{4}{5}$, czyli $y=2$. Ponadto $\frac{z}{y}=\frac{3}{5}$, czyli $\frac{z}{2}=\frac{3}{5}$, więc $z=\frac{6}{5}$.

Rozważmy trójkąt $BCF$:

RKTuDraBMcYqx

Na ilustracji przedstawiono trójkąt $ABF$. Kąt wewnętrzny przy wierzchołku B ma miarę 60 stopni. Długość boku $BC$ wynosi 4, natomiast długość boku $BF$ wynosi dwa.

Z twierdzenia cosinusów otrzymujemy ${\left|CF\right|}^2=16+4-16·\frac{1}{2}=12$, więc $\left|CF\right|=2\sqrt{3}$. Oznaczamy kąt $CEF$ przez $\gamma$. Wówczas z twierdzenia cosinusów dla trójkąta $CEF$ otrzymujemy:

${\left|CF\right|}^2={\left|CE\right|}^2+{\left|EF\right|}^2-2·\left|CE\right|·\left|EF\right|\cos \gamma$,

$12=\frac{336}{25}+\frac{36}{25}-\frac{48\sqrt{21}}{25}\cos \gamma$,

$48\sqrt{21}\cos \gamma =72$,

$\cos \gamma =\frac{3}{2\sqrt{21}}=\frac{3\sqrt{21}}{42}\approx 0,3273$.

Z tablicy wartości funkcji trygonometrycznych odczytujemy $\gamma \approx 71°$.

suma dwóch półpłaszczyzn o wspólnej krawędzi i jednego z dwóch obszarów, które te półpłaszczyzny wycinają z przestrzeni.

kąt płaski będący częścią wspólną kąta dwuściennego oraz płaszczyzny prostopadłej do jego krawędzi.

część przestrzeni ograniczona przez powierzchnię wyznaczoną przez trzy półproste o wspólnym początku nieleżące w jednej płaszczyźnie; półproste te nazywamy krawędziami kąta trójściennego, a ich wspólny początek wierzchołkiem kąta trójściennego