Przeczytaj

Przypomnijmy definicję okręgu opisanego na trójkącie.

Już wiesz

Okrąg jest opisany na trójkącie, gdy każdy wierzchołek trójkąta należy do tego okręgu.

R1IoC8AljF7Fb

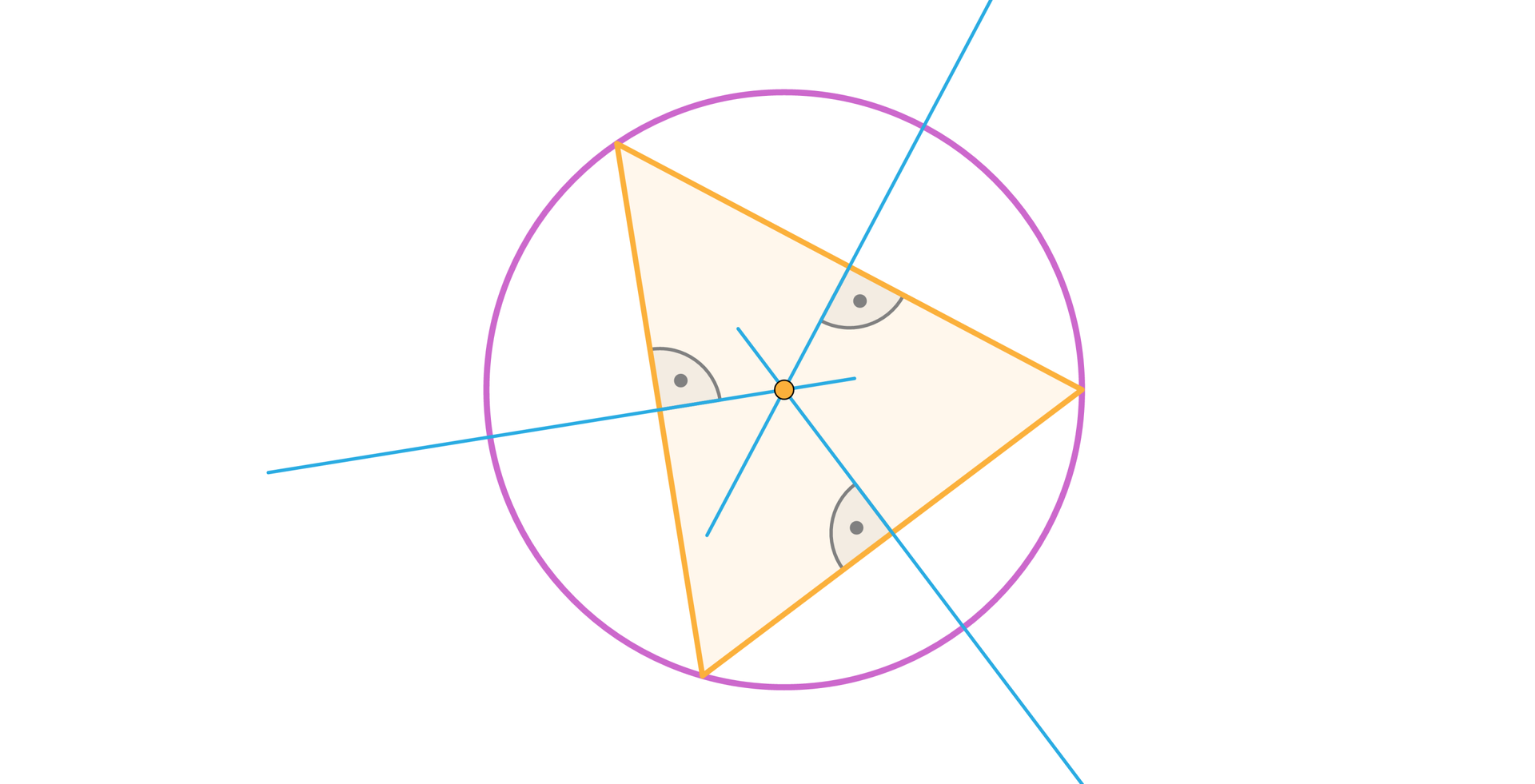
Ilustracja przedstawia trójkąt wpisany w okrąg. Trzy symetralne przechodzące przez środki boków przecinają się w punkcie będącym środkiem okręgu.

Aby wyznaczyć środek okręgu opisanego na trójkącie należy skonstruować symetralnesymetralna boku trójkątasymetralne jego boków.

Punkt przecięcia symetralnych boków trójkąta jest środkiem okręgu opisanego na tym trójkącie.

Wyznaczymy, jaka jest długość promienia okręgu opisanego na trójkącie, w zależności od rodzaju trójkąta.

1. Długość promienia okręgu opisanego na trójkącie prostokątnym.

R5vxdA6tHMTXL

Ilustracja przedstawia trójkąt prostokątny wpisany w okrąg. Przeciwprostokątna trójkąta jest jednocześnie średnicą okręgu o długości c równiej dwóm promieniom o długości R. Krótsza przyprostokątna ma długość b natomiast dłuższa długość a.

Ponieważ środek okręgu opisanego jest środkiem przeciwprostokątnej, zatem długość $R$ promienia okręgu opisanego na trójkącie prostokątnym o przyprostokątnych długości $a$ , $b$ oraz przeciwprostokątnej długości $c$ jest równa:

R = \frac{c}{2}

2. Długość promienia okręgu opisanego na trójkącie równobocznym.

RMJF1Vhd5Ne83

Ilustracja przedstawia trójkąt równoboczny o boku długości a, wpisany w okrąg o środku R. Dwie wysokości trójkąta przecinają się w środku okręgu R.

Środkowe, wysokości oraz symetralne boków trójkąta równobocznego przecinają się w punkcie, będącym środkiem okręgu opisanego na tym trójkącie. Punkt ten dzieli każdą ze środkowych w stosunku $2 : 1$ .

RpaEFtUvOdT7Z

Ilustracja przedstawia trójkąt równoboczny o boku długości a wpisany w okrąg. Dwie wysokości trójkąta przecinają się w środku okręgu. Środek okręgu podzielił jedną z wysokości na odcinki, krótszy znajdujący się przy podstawi o długości 1h3 i dłuższy od strony wierzchołka 2h3.

Zatem promień okręgu opisanego na trójkącie równobocznym o boku długości $a$ i wysokości $h$ jest równy:

R = \frac{2}{3} \cdot h = \frac{2}{3} \cdot a \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{3} a

3. Długość promienia okręgu opisanego na dowolnym trójkącie.

R1dFmqzpHBTum

Ilustracja przedstawia trójkąt wpisany w okrąg. Długości boków trójkąta mają wartości a,b oraz c. Zaznaczone są trzy promienie o długości R dochodzące do wierzchołków trójkąta oraz kąt α przy bokach c i b .

Z twierdzenia sinusówtwierdzenie sinusówtwierdzenia sinusów wiemy, że prawdziwa jest równość: $\frac{a}{\sin α} = 2 R$ .
Wobec tego:
$R = \frac{a}{2 \sin α}$ .

Ponieważ pole trójkąta wyraża się wzorem $P = \frac{1}{2} \cdot b \cdot c \cdot \sin α$ , to długość promienia okręgu opisanego na dowolnym trójkącie o bokach długości $a, b, c$ jest równa:

R = \frac{a b c}{4 P}

Ponieważ pole trójkąta wyraża się wzorem $P = r \cdot p$ , gdzie $r$ jest promieniem okręgu wpisanego w trójkąt oraz $p = \frac{a + b + c}{2}$ , zatem długość promienia okręgu opisanego na dowolnym trójkącie jest równa:
$R = \frac{a b c}{4 r p}$ .

Przykład 1

Obliczymy długość promienia okręgu opisanego na trójkącie o boku $a = 8$ i kącie $α = 120 °$ leżącym naprzeciwko boku $a$ .

Rozwiązanie:

Do wyznaczenia długości promienia okręgu opisanego na trójkącie wykorzystamy wzór $R = \frac{a}{2 \sin α}$ .

Wobec tego $R = \frac{8}{2 \cdot \sin 120 °} = \frac{8}{2 \cdot \sin 60 °} = \frac{4}{\sin 60 °} = \frac{4}{\frac{\sqrt{3}}{2}} = \frac{8 \sqrt{3}}{3}$ .

Nie zawsze konieczne jest wykorzystanie wyżej wymienionych wzorów. W przypadku trójkąta równoramiennego wystarczy wykorzystać twierdzenie Pitagorasa.

Przykład 2

Obliczymy długość promienia okręgu opisanego na trójkącie równoramiennym o podstawie długości $6$ i ramieniu długości $8$ .

Rozwiązanie:

Narysujmy trójkąt równoramienny i wprowadźmy odpowiednie oznaczenia:

RIvcWJ4LmbQrW

Ilustracja przedstawia trójkąt równoboczny o bokach długości 8 i długości podstawy 6, trójkąt jest wpisany w okrąg . Zaznaczone są trzy promienie o długości R dochodzące do wierzchołków trójkąta . Od środka okręgu do podstawy pod kątem prostym dochodzi przerywana linia o długości x , będąca elementem wysokości h na którą składa się również promień R.

Długość wysokości $h$ obliczymy z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa.

Wobec tego $h^{2} + 3^{2} = 8^{2}$

$h^{2} = 55$ , czyli $h = \sqrt{55}$ .

Zauważmy, że $x = h - R$ , zatem $x = \sqrt{55} - R$ .

Korzystając z twierdzenia Pitagorasa, mamy:

$x^{2} + 3^{2} = R^{2}$

${(\sqrt{55} - R)}^{2} + 3^{2} = R^{2}$

$55 - 2 \sqrt{55} R + R^{2} + 9 = R^{2}$

$R = \frac{64}{2 \sqrt{55}} = \frac{32}{\sqrt{55}} = \frac{32 \sqrt{55}}{55}$ .

Przykład 3

Obliczymy długość promienia okręgu opisanego na trójkącie prostokątnym równoramiennym o polu $P$ .

Rozwiązanie:

Narysujmy trójkąt prostokątny równoramienny i wprowadźmy odpowiednie oznaczenia:

R1AB5ck3SVY9I

Ilustracja przedstawia prostokątny równoramienny trójkąt wpisany w okrąg o przyprostokątnych długości a. Kąty ostre mają wartość 45°. Przeciwprostokątna trójkąta jest jednocześnie średnicą okręgu o długości a2.

Jeżeli pole tego trójkąta jest równe $P$ , zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$\frac{1}{2} \cdot a \cdot a = P$

$a^{2} = 2 P$ , czyli $a = \sqrt{2 P}$ .

Przeciwprostokątna tego trójkąta ma długość $a \sqrt{2} = \sqrt{2 P} \cdot \sqrt{2} = 2 \sqrt{P}$ .

Do wyznaczenia długości promienia okręgu opisanego na tym trójkącie wykorzystamy wzór $R = \frac{c}{2}$ .

Zatem $R = \frac{2 \sqrt{P}}{2} = \sqrt{P}$ .

Przykład 4

Obliczymy długość promienia okręgu opisanego na trójkącie równobocznym, którego pole wynosi $P$ .

Rozwiązanie:

Pole trójkąta równobocznego o boku $a$ obliczamy ze wzoru $P = \frac{a^{2} \sqrt{3}}{4}$ , zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$P = \frac{a^{2} \sqrt{3}}{4}$ .

Wobec tego $4 P = a^{2} \sqrt{3}$ , zatem $a^{2} = \frac{4 P}{\sqrt{3}} = \frac{4 P \sqrt{3}}{3}$ , czyli $a = \sqrt{\frac{4 P \sqrt{3}}{3}}$ .

Do wyznaczenia długości promienia $R$ okręgu opisanego na tym trójkącie wykorzystamy wzór $R = \frac{a \sqrt{3}}{3}$ .

Zatem $R = \frac{\sqrt{\frac{4 P \sqrt{3}}{3}} \cdot \sqrt{3}}{3} = \frac{\sqrt{4 P \sqrt{3}}}{3}$ .

Przykład 5

Obliczymy długość promienia okręgu opisanego na trójkącie o bokach długości $3, 4, 6$ .

Rozwiązanie:

Narysujmy rysunek pomocniczy i wprowadźmy odpowiednie oznaczenia.

R1aX3lQX9Vtum

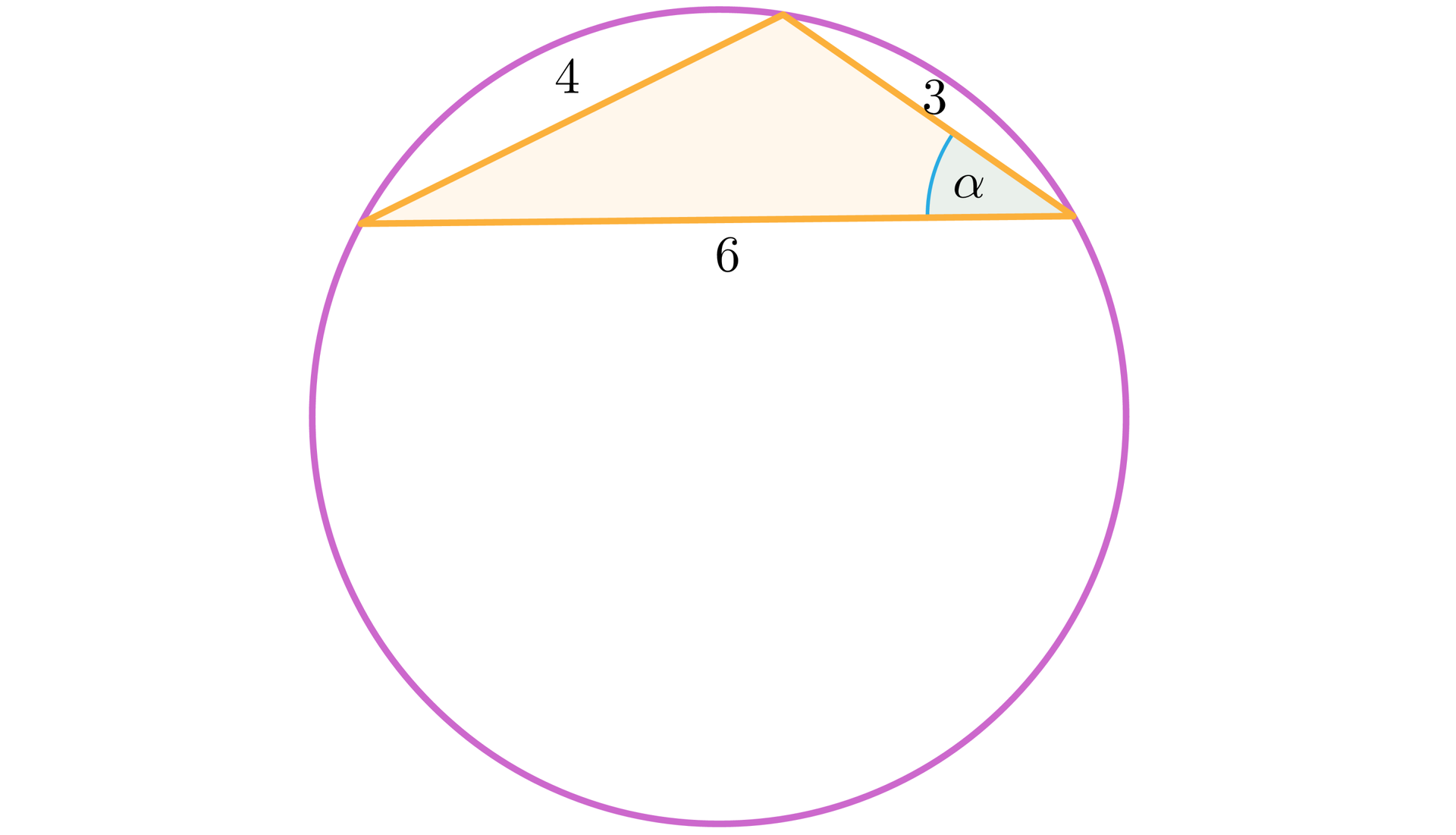
Ilustracja przedstawia pomarańczowy trójkąt wpisany w okrąg. Boki trójkąta mają długości 6, 4 i 3 a kąt między bokami długości 6 i 3 ma wartość α.

Obliczmy cosinus kąta $α$ z wykorzystaniem twierdzenia cosinusówtwierdzenie cosinusówtwierdzenia cosinusów.

Zatem

$4^{2} = 3^{2} + 6^{2} - 2 \cdot 3 \cdot 6 \cdot \cos α$

$16 = 9 + 36 - 36 \cdot \cos α$ , czyli $\cos α = \frac{29}{36}$ .

Do wyznaczenia wartości sinusa kąta wykorzystamy jedynkę trygonometrycznąjedynka trygonometrycznajedynkę trygonometryczną:

$\sin^{2} α + \cos^{2} α = 1$

$\sin^{2} α + {(\frac{29}{36})}^{2} = 1$

$\sin^{2} α + \frac{841}{1296} = 1$

$\sin^{2} α = \frac{455}{1296}$ , więc $\sin α = \frac{\sqrt{455}}{36}$ lub $\sin α = - \frac{\sqrt{455}}{36}$ .

Kąt $α$ jest ostry, zatem $\sin α = \frac{\sqrt{455}}{36}$ .

Do wyznaczenia długości promienia okręgu opisanego wykorzystamy wzór:

$R = \frac{a}{2 \sin α}$

Wobec tego $R = \frac{4}{2 \cdot \frac{\sqrt{455}}{36}} = \frac{72}{\sqrt{455}} = \frac{72 \sqrt{455}}{455}$ .

Słownik

symetralna boku trójkąta

prosta prostopadła do boku, dzieląca go na dwie równe części

jedynka trygonometryczna

wzór postaci $\sin^{2} α + \cos^{2} α = 1$

twierdzenie Pitagorasa

w trójkącie prostokątnym kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych

twierdzenie sinusów

w dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta leżącego naprzeciw boku jest równy długości średnicy okręgu opisanego na tym trójkącie

twierdzenie cosinusów

w dowolnym trójkącie kwadrat dowolnego boku równa się sumie kwadratów długości dwóch pozostałych boków pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta zawartego między nimi

Wprowadzenie

Animacja

Słownik