Przeczytaj

Na początek podamy definicję podobieństwa.

Podobieństwo o skali

s

Definicja: Podobieństwo o skali

s

Podobieństwemskala podobieństwa figurPodobieństwem o skali $s > 0$ nazywamy takie przekształcenie $P$ płaszczyzny na tę samą płaszczyznę (mówimy wówczas o podobieństwie płaszczyzny) lub przestrzeni na tę samą przestrzeń (mówimy wówczas o podobieństwie przestrzeni), w którym

|A^{'} B^{'}| = s \cdot |A B|

gdzie:
$A$ i $B$ – są dwoma dowolnymi punktami,
$A^{'}$ i $B^{'}$ – obrazami tych punktów w przekształceniu $P$ .

Wtedy definicja figur podobnych mogłaby być sformułowana następująco:

Figury podobne

Definicja: Figury podobne

Figury nazywamy podobnymi wtedy, gdy jedna z nich jest obrazem drugiej w pewnym podobieństwie. Relację podobieństwa figur oznaczamy symbolem „ $~$ ”. Zatem fakt, że figura $f$ jest podobna do figury $g$ możemy zapisać krótko

f ~ g

Skalę $s > 0$ tego podobieństwa nazywamy wtedy skalą podobieństwa figury $f$ do figury $g$

Przykładami figur podobnych są:

dowolne dwa odcinki,

dowolne dwa okręgi,

dowolne dwa wielokąty foremne o tej samej liczbie boków (trójkąty równoboczne, kwadraty, pięciokąty foremne, itd.)

Podana definicja nie daje nam jednak dobrego narzędzia do badania podobieństwa figur. Ponieważ każdy wielokąt można poddać tzn. triangulacji, czyli podzielić ten wielokąt na trójkąty (można to zrobić zawsze tak, żeby wszystkie wierzchołkami tych trójkątów były wierzchołkami tego wielokąta – o tym orzeka twierdzenie o triangulacji wielokąta), więc trójkąty możemy traktować jak „cegiełki”, z których zbudowane są wielokąty. Z tego powodu wystarczy umieć rozstrzygać, czy dane trójkąty są podobne.

Wniosek o tym, że dwa trójkąty są podobne możemy wyciągnąć z każdego z następujących trzech warunków, zwanych cechami podobieństwa trójkątów:

Cecha „bok – bok – bok” podobieństwa trójkątów

Twierdzenie: Cecha „bok – bok – bok” podobieństwa trójkątów

Jeżeli długości trzech boków jednego trójkąta są proporcjonalne do długości odpowiednich trzech boków drugiego trójkąta, to te trójkąty są podobne.

Przyjmując oznaczenia jak na rysunku

RZkzEPDrMI3wY

Ilustracja przedstawia dwa trójkąty: A B C oraz większy D E F. Trójkąty są proporcjonalne, a odpowiadające sobie boki wyróżniono tymi samymi kolorami: lewe ramiona A C oraz D F granatowym, prawe ramiona B C oraz E F różowym oraz podstawy A B i D E zielonym kolorem.

Możemy to twierdzenie zapisać w postaci:

Jeżeli $\frac{|A B|}{|D E|} = \frac{|B C|}{|E F|} = \frac{|C A|}{|F D|}$ , to $△ A B C ~ △ D E F$ .

Cecha „bok – kąt – bok” podobieństwa trójkątów

Twierdzenie: Cecha „bok – kąt – bok” podobieństwa trójkątów

Jeżeli długości dwóch boków trójkąta są proporcjonalne do długości odpowiednich dwóch boków drugiego trójkąta i kąty miedzy tymi bokami w obu trójkątach są równe, to te trójkąty są podobne.

Przyjmując oznaczenia jak na rysunku

RiycRNdRrBbdT

Możemy to twierdzenie zapisać w postaci:

Jeżeli $\frac{|A B|}{|D E|} = \frac{|C A|}{|F D|}$ i $|∢ B A C| = |∢ E D F|$ , to $△ A B C ~ △ D E F$ .

Cecha „kąt – kąt – kąt” podobieństwa trójkątów

Twierdzenie: Cecha „kąt – kąt – kąt” podobieństwa trójkątów

Jeżeli trzy kąty jednego trójkąta są równe odpowiednim trzem kątom drugiego trójkąta, to te trójkąty są podobne.

Przyjmując oznaczenia jak na rysunku

R1Ti0P0lmGeN5

Możemy to twierdzenie zapisać w postaci:

Jeżeli $|∢ B A C| = |∢ E D F|$ i $|∢ A B C| = |∢ D E F|$ i $|∢ B C A| = |∢ D F E|$ , to $△ A B C ~ △ D E F$ .

Przykład 1

Rozstrzygnij, czy trójkąt o bokach długości $12$ , $18$ , $24$ jest podobny do trójkąta o bokach długości $14$ , $21$ , $28$ .

Rozwiązanie

Stosunek długości najkrótszych boków tych trójkątów jest równy $\frac{12}{14} = \frac{6}{7}$ .

Stosunek długości najdłuższych boków jest równy $\frac{24}{28} = \frac{6}{7}$ , a stosunek długości pozostałych boków jest równy $\frac{18}{21} = \frac{6}{7}$ .

Wszystkie trzy stosunki są równe, więc z cechy bbb wynika, że te trójkąty są podobne.

Skala podobieństwa pierwszego z nich do drugiego jest równa $\frac{6}{7}$ , natomiast skala podobieństwa drugiego z nich do pierwszego jest równa $\frac{7}{6}$ .

Przykład 2

Długości boków trójkąta $A B C$ są równe: $45$ , $39$ i $12$ . W trójkącie $K L M$ dane są: $|K L| = 8$ , $|K M| = 30$ , $\cos (∢ M K L) = 0, 6$ . Rozstrzygnij, czy te trójkąty są podobne.

Rozwiązanie

Obliczymy najpierw długość boku $L M$ trójkąta $K L M$ .

Z twierdzenia cosinusów otrzymujemy

${|L M|}^{2} = {|K L|}^{2} + {|K M|}^{2} - 2 \cdot |K L| \cdot |K M| \cdot \cos |∢ M K L|$ czyli ${|L M|}^{2} = 8^{2} + 30^{2} - 2 \cdot 8 \cdot 30 \cdot 0, 6 = 676$ .

Stąd $|L M| = \sqrt{676} = 26$ .

Teraz, mając już długości wszystkich boków obu trójkątów możemy obliczyć stosunki długości odpowiednich boków.

Ponieważ $\frac{45}{30} = \frac{39}{26} = \frac{12}{8} (= \frac{3}{2})$ , więc z cechy bbb wnioskujemy, że trójkąty $A B C$ i $K L M$ są podobne.

Przykład 3

Przekątne $A C$ i $B D$ trapezu $A B C D$ o podstawach $A B$ i $C D$ przecinają się w punkcie $S$ .

RuyJYf1uihm0V

Ilustracja przedstawia trapez A B C D w którym poprowadzono przekątne A C oraz B D przecinające się w punkcie S. A B jest dolną podstawa, a D C górną.

Uzasadnij, że trójkąty $A B S$ i $C D S$ są podobne.

Rozwiązanie

Kąty $B A S$ i $D C S$ są naprzemianległe oraz kąty $A B S$ i $C D S$ są naprzemianległe.

Proste $A B$ i $C D$ są równoległe, gdyż czworokąt $A B C D$ jest trapezem, więc z twierdzenia o kątach naprzemianległych wynika, że $|∢ B A S| = |∢ D C S|$ oraz $|∢ A B S| = |∢ C D S|$ .

Kąty $A S B$ i $C S D$ są wierzchołkowe, więc $|∢ A S B| = |∢ C S D|$ .

R1WSTdJIcRmo3

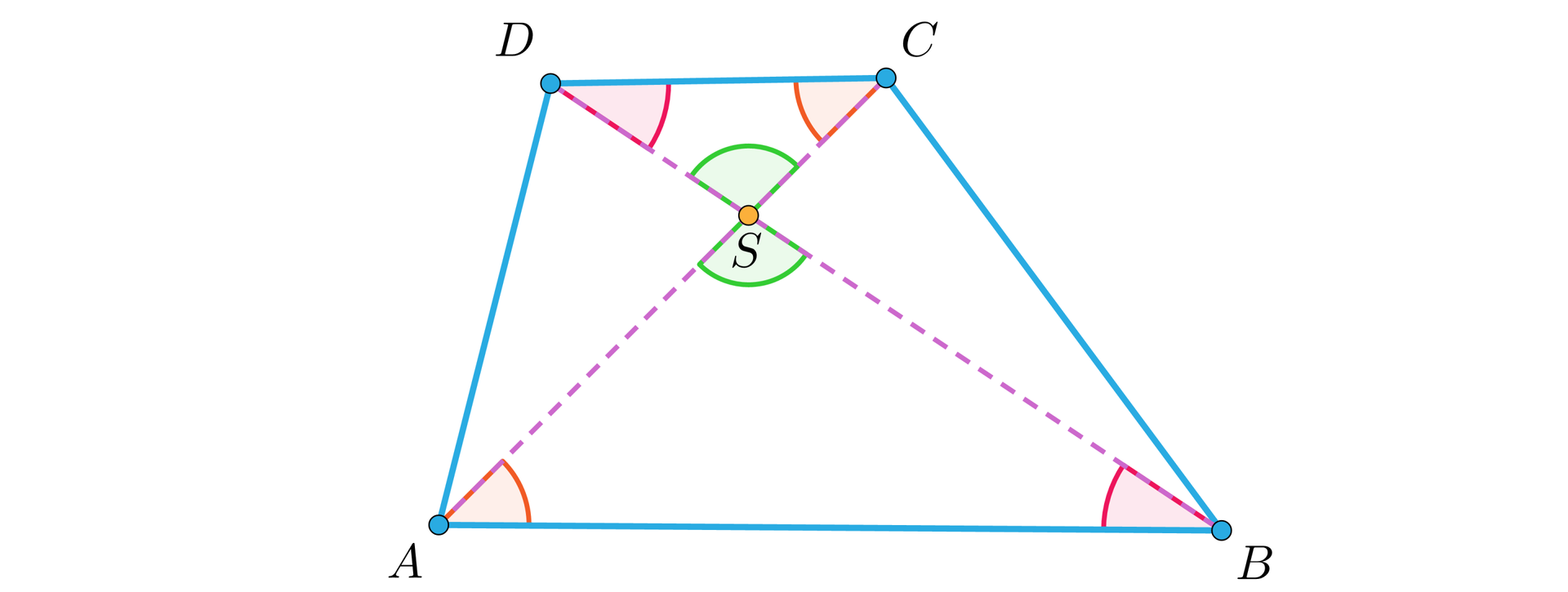
Ilustracja przedstawia trapez A B C D w którym poprowadzono przekątne A C oraz B D przecinające się w punkcie S. A B jest dolną podstawa, a D C górną. Zaznaczono następujące kąty: kąt A S B oraz D S C są równe. Kąty B D C oraz D B A są równe. Kąty A C D oraz C A B są równe.

Zatem z cechy kkk wynika, że trójkąty $A B S$ i $C D S$ są podobne.

Przykład 4

Przekątne $A C$ i $B D$ trapezu $A B C D$ , którego podstawy $A B$ i $C D$ mają długości $|A B| = a$ i $|C D| = b$ , przecinają się w punkcie $S$ .

R1301JS9DnKvI

Ilustracja przedstawia trapez A B C D w którym poprowadzono przekątne A C oraz B D przecinające się w punkcie S. Odcinek A B oznaczony małą literą a jest dolną podstawa, a odcinek D C oznaczony małą literą b to górna podstawa.

Wykaż, że stosunek pola trójkąta $A B S$ do pola trapezu $A B C D$ jest równy ${(\frac{a}{a + b})}^{2}$ .

Dowód

Ru6WKT7J1NiPH

Krok 1
Uzasadnij, że stosunek pola trójkąta $A D S$ do pola trójkąta $C D S$ jest równy $\frac{"|"A S"|"}{"|"C S"|"}$ , czyli $\frac{P_{A D S}}{P_{C D S}} = \frac{"|"A S"|"}{"|"C S"|"}$ .

Uzasadnienie Kroku 1
Trójkąty $A D S$ i $C D S$ mają wspólną wysokość opuszczoną z wierzchołka $D$ . Oznaczając tę wysokość literą $h$ otrzymujemy
$\frac{P_{A D S}}{P_{C D S}} = \frac{\frac{1}{2} \cdot "|"A S"|" \cdot h}{\frac{1}{2} \cdot "|"C S"|" \cdot h} = \frac{"|"A S"|"}{"|"C S"|"}$ .

Krok 2
Uzasadnij, że prawdziwa jest równość $\frac{P_{A D S}}{P_{C D S}} = \frac{P_{A B S}}{P_{C B S}}$ .

Uzasadnienie Kroku 2
Z własności, której prawdziwość uzasadniliśmy w kroku 1. wynika, że $\frac{P_{A D S}}{P_{C D S}} = \frac{"|"A S"|"}{"|"C S"|"}$ i $\frac{P_{A B S}}{P_{C B S}} = \frac{"|"A S"|"}{"|"C S"|"}$ .
Stąd wynika równość $\frac{P_{A D S}}{P_{C D S}} = \frac{P_{A B S}}{P_{C B S}}$ .

Krok 3
Uzasadnij, że trójkąty $A B S$ i $C D S$ są podobne.

Uzasadnienie Kroku 3
Proste $A B$ i $C D$ są równoległe. Kąty $B A S$ i $D C S$ są naprzemianległe oraz kąty $A B S$ i $C D S$ są naprzemianległe, więc $"|"∢ B A S"|" = "|"∢ D C S"|"$ oraz $"|"∢ A B S"|" = "|"∢ C D S"|"$ .
Kąty $A S B$ i $C S D$ są wierzchołkowe, więc $"|"∢ A S B"|" = "|"∢ C S D"|"$ .
Zatem z cechy kkk wynika, że trójkąty $A B S$ i $C D S$ są podobne.

Krok 4
Uzasadnij, że $\frac{P_{A B S}}{P_{C D S}} = {(\frac{a}{b})}^{2}$ .

Uzasadnienie Kroku 4
Trójkąty $A B S$ i $C D S$ są podobne, a skala ich tego podobieństwa jest równa stosunkowi odpowiednich długości w tych trójkątach, więc jest równa $\frac{"|"A B"|"}{"|"C D"|"} = \frac{a}{b}$ .
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa tych figur, więc $\frac{P_{A B S}}{P_{C D S}} = {(\frac{a}{b})}^{2}$ .

Krok 5
Uzasadnij, że $P_{A D S} = P_{C B S}$ .

Uzasadnienie Kroku 5
Kąty $A S D$ i $B S C$ są wierzchołkowe, więc $"|"∢ A S D"|" = "|"∢ B S C"|"$ . Oznaczmy miarę tych kątów przez $φ$ .
Z podobieństwa trójkątów $A B S$ i $C D S$ , co wykazaliśmy w kroku 3., wynika, że $\frac{"|"A S"|"}{"|"B S"|"} = \frac{"|"C S"|"}{"|"D S"|"}$ . Stąd $"|"A S"|" \cdot "|"D S"|" = "|"B S"|" \cdot "|"C S"|"$ .
Mnożąc obie strony tej równości przez $\frac{1}{2} \sin φ$ otrzymujemy równość $\frac{1}{2} \cdot "|"A S"|" \cdot "|"D S"|" \cdot \sin φ = \frac{1}{2} \cdot "|"B S"|" \cdot "|"C S"|" \cdot \sin φ$ .
Stąd i ze wzoru na pole trójkąta z sinusem otrzymujemy $P_{A D S} = P_{C B S}$ .

Krok 6
Uzasadnij, że $P_{A D S} = \frac{b}{a} \cdot P_{A B S}$ .

Uzasadnienie Kroku 6
Z równości $\frac{P_{A D S}}{P_{C D S}} = \frac{P_{A B S}}{P_{C B S}}$ i $P_{A D S} = P_{C B S}$ wykazanych w krokach 2. i 5. otrzymujemy kolejno
$P_{A D S} \cdot P_{C B S} = P_{C D S} \cdot P_{A B S}$ ,
${(P_{A D S})}^{2} = P_{C D S} \cdot P_{A B S}$ .
Stąd i z równości $\frac{P_{A B S}}{P_{C D S}} = {(\frac{a}{b})}^{2}$ , której prawdziwość wykazaliśmy w kroku 4. wynika, że ${(P_{A D S})}^{2} = {(\frac{b}{a})}^{2} \cdot P_{A B S} \cdot P_{A B S} = {(\frac{b}{a} \cdot P_{A B S})}^{2}$ , skąd dostajemy $P_{A D S} = \frac{b}{a} \cdot P_{A B S}$ .

Krok 7
Uzasadnij, że $\frac{P_{A B S}}{P_{A B C D}} = {(\frac{a}{a + b})}^{2}$ .

Uzasadnienie Kroku 7
$\frac{P_{A B S}}{P_{A B C D}} = \frac{P_{A B S}}{P_{A B S} + P_{A D S} + P_{C B S} + P_{C D S}} = \frac{P_{A B S}}{P_{A B S} + 2 P_{A D S} + P_{C D S}} =$
$= \frac{P_{A B S}}{P_{A B S} + 2 (\frac{b}{a} \cdot P_{A B S}) + {(\frac{b}{a})}^{2} \cdot P_{A B S}} = \frac{P_{A B S}}{P_{A B S} (1 + 2 \cdot \frac{b}{a} + {(\frac{b}{a})}^{2})} =$
$= \frac{1}{1 + 2 \cdot \frac{b}{a} + {(\frac{b}{a})}^{2}} = \frac{1}{{(1 + \frac{b}{a})}^{2}} = \frac{1^{2}}{{(\frac{a + b}{a})}^{2}} = {(\frac{1}{\frac{a + b}{a}})}^{2} = {(\frac{a}{a + b})}^{2}$

Słownik

skala podobieństwa figur

jeżeli figura $g$ jest obrazem figury $f$ w podobieństwie o skali $s > 0$ , to liczbę $s$ nazywamy skalą podobieństwa tych figur (dokładniej skalą podobieństwa figury $g$ do figury $f$ )

Wprowadzenie

Film edukacyjny

Słownik