Podstawą ostrosłupa $ABCDS$ jest równoległobok $ABCD$ o bokach długości $\left|AB\right|=5$ i $\left|AD\right|=4$ oraz przekątnej $BD$ długości $3$. Wysokością ostrosłupa jest krawędź $SD$ o długości $2$. Obliczymy pole ściany bocznej $BSC$.

Rozwiązanie:

Wykonajmy rysunek pomocniczy:

Rp1ZAPUIVkhBd

Ilustracja przedstawia ostrosłup o podstawie równoległoboku. Wierzchołki podstawy to A B C D, przy czym odcinek AD ma długość 4, natomiast odcinek AB ma długość pięć. Wierzchołek ostrosłupa podpisano literą S. Krawędź boczna SD jest pod kątem prostym do krawędzi podstawy i ma długość dwa. W podstawie zaznaczono jej przekątną BD, ma ona długość trzy.

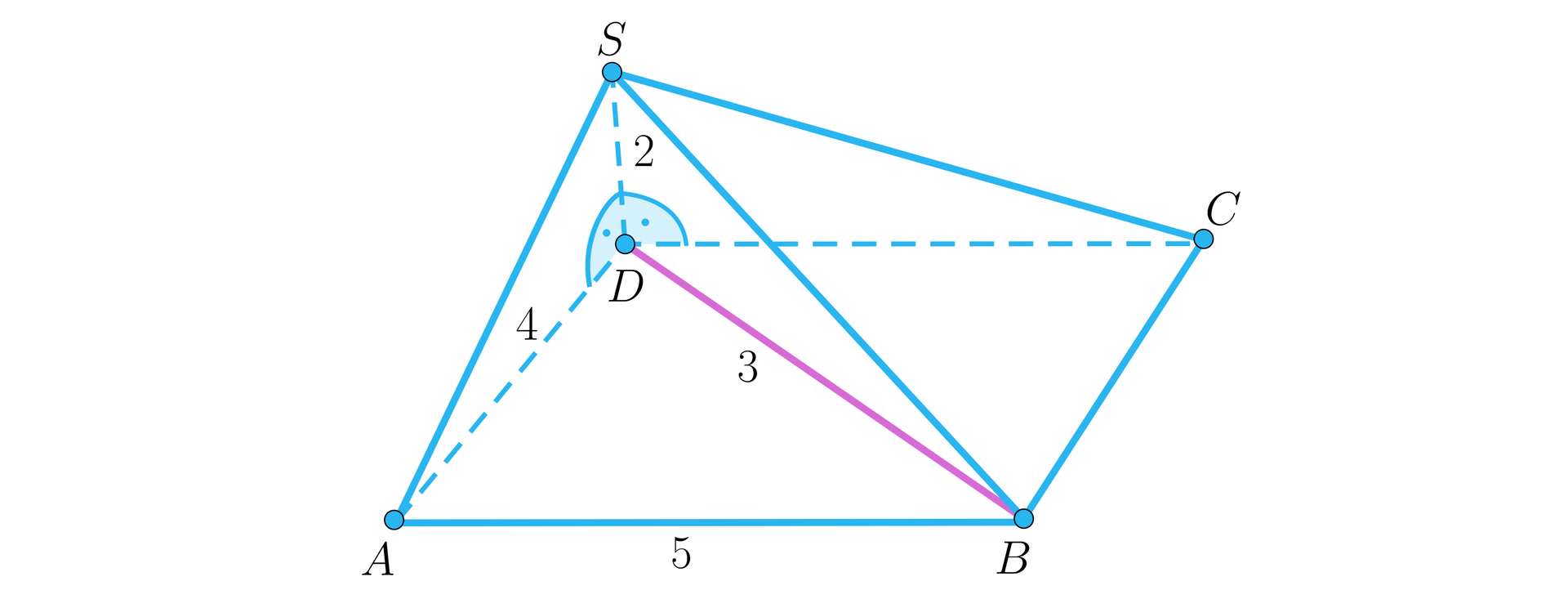
Trójkąt $ADB$ jest prostokątny (trójkąt egipski).

Trójkąty $SDC$ i $SDB$ są prostokątne, więc na mocy twierdzenia Pitagorasa mamy:

$\left|SC\right|=\sqrt{2^2+5^2}=\sqrt{29}$

$\left|SB\right|=\sqrt{2^2+3^2}=\sqrt{13}$.

Zauważmy, że:

${\sqrt{13}}^2+4^2={\sqrt{29}}^2$

$29=29$.

Zatem na podstawie twierdzenia odwrotnego do twierdzenia Pitagorasa możemy stwierdzić, że trójkąt $BSC$ jest prostokątny.

Zauważmy, że prosta $DB$ jest rzutem prostokątnym prostej $SB$ na płaszczyznę oraz kąt $DBC$ jest prosty. Na podstawie twierdzenia o trzech prostych prostopadłych możemy stwierdzić, bez wykonywania obliczeń, że prosta $SB$ jest prostopadła do $BC$.

Jego pole wynosi:

$P=\frac{1}{2}·\sqrt{13}·4=2\sqrt{13}$.

Podstawą ostrosłupa jest prostokąt $ABCD$, a krawędź $DS$ jest jego wysokością o długości $15 \mathrm{cm}$. Obliczymy pole powierzchni całkowitej ostrosłupa wiedząc, że najdłuższa krawędź boczna ma długość $\frac{25\sqrt{10}}{4} \mathrm{cm}$ a stosunek długości boków prostokąta wynosi $5:9$.

Rozwiązanie:

Wykonajmy rysunek pomocniczy:

RfDSMZ82OEazi

Ilustracja przedstawia ostrosłup o podstawie równoległoboku. Wierzchołki podstawy to A B C D. Wierzchołek ostrosłupa podpisano literą S. Krawędź boczna SD jest pod kątem prostym do krawędzi podstawy i ma długość piętnaście. W podstawie linią przerywaną zaznaczono jej przekątną BD. Krawędź boczna BS ma długość $\frac{{\displaystyle 25\sqrt{10}}}{4}$.

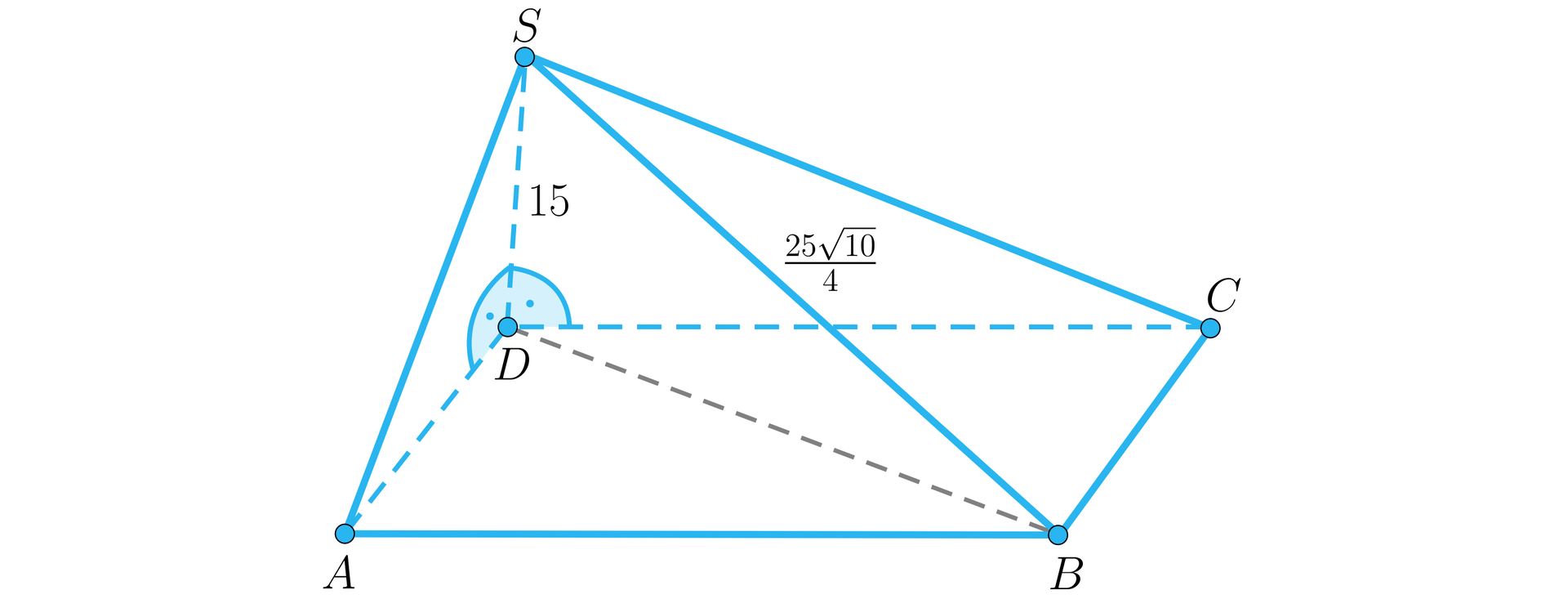
Skoro stosunek boków prostokąta wynosi $5:9$, to dłuższy bok możemy oznaczyć jako $9x$, a krótszy $5x$.

Obliczmy długość przekątnej prostokąta:

${\left|DB\right|}^2={\left(9x\right)}^2+{\left(5x\right)}^2$

${\left|DB\right|}^2={81x}^2+{25x}^2$

${\left|DB\right|}^2=106x^2$

$\left|DB\right|=x\sqrt{106}$.

Trójkąt $SDB$ jest prostokątny, więc z twierdzenia Pitagorasa mamy:

${15}^2+{\left(x\sqrt{106}\right)}^2={\left(\frac{25\sqrt{10}}{4}\right)}^2$

$225+106x^2=\frac{6250}{16}$

$106x^2=\frac{2650}{16}$

$x^2=\frac{25}{16}$

$x=\frac{5}{4}$.

Zatem boki prostokąta mają długość:

$9x=9·\frac{5}{4}=\frac{45}{4}$

$5x=5·\frac{5}{4}=\frac{25}{4}$.

Pole podstawy ostrosłupa wynosi więc:

$P_p=\frac{45}{4}·\frac{25}{4}=\frac{1125}{16}$.

Zajmijmy się teraz polem powierzchni bocznej. Trójkąty $SDC$ i $SDA$ są prostokątne. Obliczmy ich przeciwprostokątne:

${\left|SC\right|}^2={15}^2+{\left(\frac{45}{4}\right)}^2$

$\left|SC\right|=\frac{75}{4}$

${\left|SA\right|}^2={15}^2+{\left(\frac{25}{4}\right)}^2$

$\left|SA\right|=\frac{65}{4}$.

Zauważmy, że trójkąty $SAB$ i $SBC$ są prostokątne, gdyż:

${\left|SA\right|}^2+{\left|AB\right|}^2={\left|SB\right|}^2$

oraz

${\left|SC\right|}^2+{\left|BC\right|}^2={\left|SB\right|}^2$.

Pole powierzchni bocznej to zatem suma pól czterech trójkątów prostokątnych:

$P_b=\frac{1}{2}·15·\frac{45}{4}+\frac{1}{2}·15·\frac{25}{4}+\frac{1}{2}·\frac{65}{4}·\frac{45}{4}+\frac{1}{2}·\frac{75}{4}·\frac{25}{4}=$

$=\frac{675}{8}+\frac{375}{8}+\frac{2925}{32}+\frac{1875}{32}=\frac{1125}{4}=281\frac{1}{4}$.

Obliczmy więc pole powierzchni całkowitej:

$P_c=\frac{1125}{16}+281\frac{1}{4}=70\frac{5}{16}+281\frac{4}{16}=351\frac{9}{16} {\mathrm{cm}}^2$.

Podstawą ostrosłupa jest romb o boku długości $a$ i kącie ostrym $30°$. Wysokość ostrosłupa jest równa $2a$, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Obliczymy pole powierzchni ostrosłupa.

Rozwiązanie:

Wykonajmy rysunek pomocniczy. Wprowadźmy dodatkowe oznaczenie.

Niech $h$ – wysokość rombu.

R1GjGY2aUhMyK

Ilustracja przedstawia ostrosłup o podstawie rombu. Wierzchołki podstawy to A B C D, długość boku wynosi a, kąt CAD ma miarę 30 stopni. W podstawie linią przerywaną zaznaczono jej przekątną AC, zaznaczono również jej wysokość h wychodzącą z wierzchołka D i opuszczoną na bok AB. Wierzchołek ostrosłupa podpisano literą S, z wierzchołka tego poprowadzono wysokość ostrosłupa, spodek wysokości podpisano literą E, spodek ten leży na przekątnej podstawy AC. Wysokość ma długość 2a. Na krawędzi podstawy AB zaznaczono punkt F. Odcinki SE, EF oraz SF tworzą trójkąt prostokątny, przy czym odcinek SF zawarty w płaszczyźnie ściany bocznej ABS jest przeciwprostokątną w tym trójkącie.

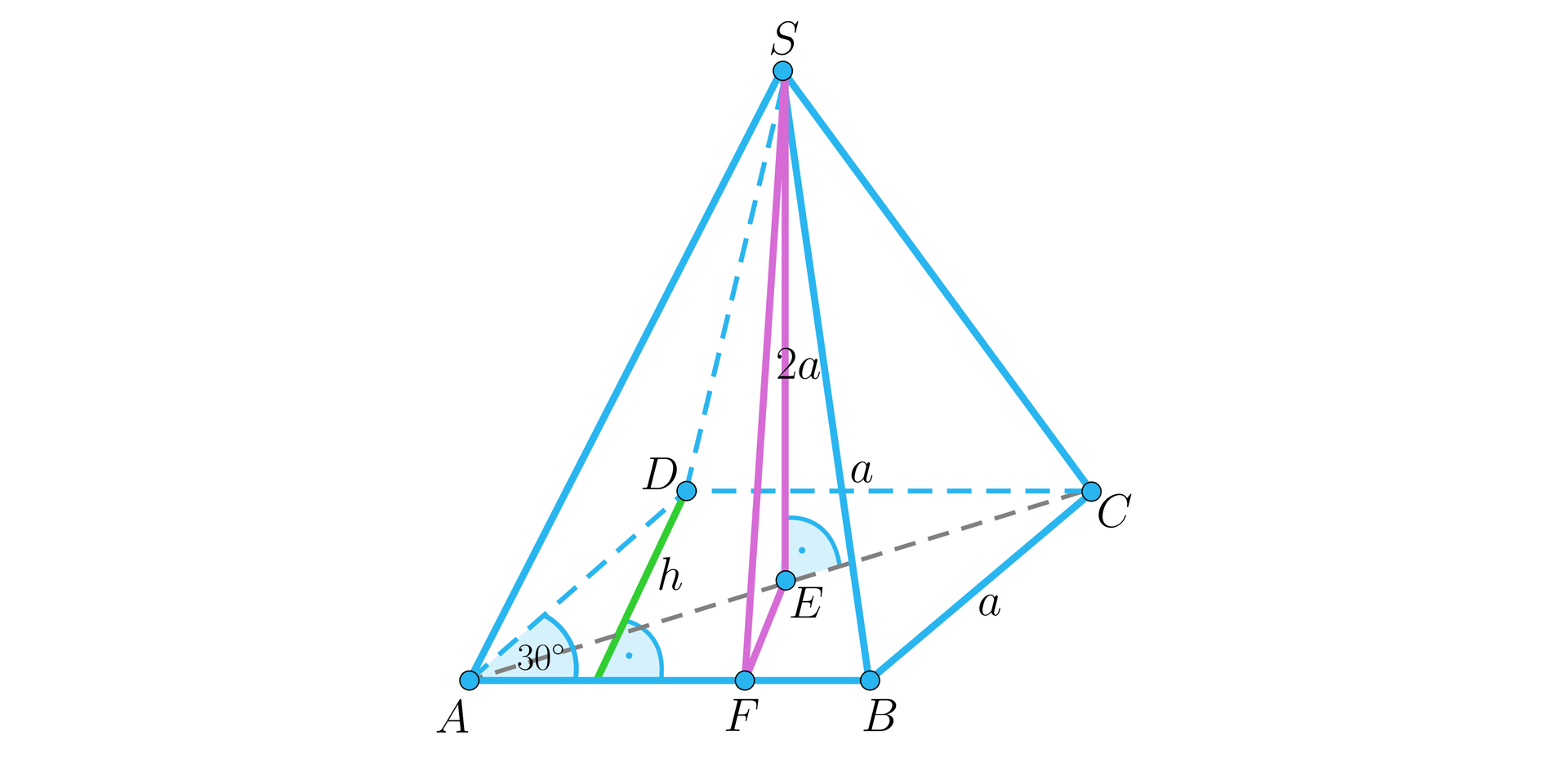
Skoro kąt ostry naszego rombu ma miarę $30°$, to znaczy, że wysokość rombu ma długość $\frac{1}{2}a$.

Zatem $P_p=a·\frac{1}{2}a=\frac{a^2}{2}$.

Promień okręgu wpisanego w romb jest równy połowie jego wysokości, zatem $r=\frac{1}{4}a$.

Trójkąt $SEF$ jest prostokątny, co w łatwy sposób pozwoli nam policzyć wysokość ściany bocznej ostrosłupa:

${\left(2a\right)}^2+{\left(\frac{1}{4}a\right)}^2={\left|SF\right|}^2$

$\left|SF\right|=\sqrt{4a^2+\frac{1}{16}{a}^2}=\sqrt{\frac{65}{16}{a}^2}=\frac{a\sqrt{65}}{4}$

$P_{śb}=\frac{1}{2}·a·\frac{a\sqrt{65}}{4}=\frac{a^2\sqrt{65}}{8}$

$P_b=4·\frac{a^2\sqrt{65}}{8}=\frac{a^2\sqrt{65}}{2}$

$P_c=\frac{a^2}{2}+\frac{a^2\sqrt{65}}{2}=\frac{a^2}{2}\left(1+\sqrt{65}\right)$.

Podstawą ostrosłupa czworokątnego prostegoostrosłup czworokątny prostyostrosłupa czworokątnego prostego jest prostokąt, w którym miary kątów płaskich przy wierzchołku ostrosłupakąt płaski przy wierzchołku ostrosłupa prawidłowegokątów płaskich przy wierzchołku ostrosłupa mają miary $\alpha$ i $\beta$. Pole powierzchni bocznej ostrosłupa wynosi $P^2\left(\sin \alpha +\sin \beta \right)$. Obliczymy pole podstawy tego ostrosłupa.

Rozwiązanie:

Wykonajmy rysunek pomocniczy. Wprowadźmy dodatkowe oznaczenie.

Niech $x$ – długość krawędzi bocznych, $a$ i $b$ – krawędzie podstawy.

RUYPfYZQJuBKl

Ilustracja przedstawia ostrosłup czworokątny prosty, którego podstawą jest prostokąt A B C D. Bok AB ma długość b, a bok BC ma długość a. Wierzchołek ostrosłupa podpisano literą S. Krawędzie boczne BS i CS podpisano literą x. Kąt BSC podpisano literą alfa. Kąt ASB podpisano literą beta.

Pole ściany bocznej $BSC$ możemy policzyć ze wzoru $\frac{1}{2}{x}^2\sin \alpha$, ściany $ASB$ – $\frac{1}{2}{x}^2\sin \beta$.

Zatem $P_b=2·\frac{1}{2}{x}^2\sin \alpha +2·\frac{1}{2}{x}^2\sin \beta =x^2\left(\sin \alpha +\sin \beta \right)$.

Z treści zadania wiemy, że $P_b=P^2\left(\sin \alpha +\sin \beta \right)$. Zatem:

$x^2=P^2$

$x=P$.

Z twierdzenia cosinusów obliczmy krawędzie podstawy:

$a^2=P^2+P^2-2P^2\cos \alpha$ oraz $b^2=P^2+P^2-2P^2\cos \beta$,

$a^2=P^2\left(2-2\cos \alpha \right)$ oraz $b^2=P^2\left(2-2\cos \beta \right)$,

$a=P\sqrt{2-2\cos \alpha }$ i $b=P\sqrt{2-2\cos \beta }$.

Zatem pole podstawy wynosi:

$P_p=ab=P^2\sqrt{\left(2-2\cos \alpha \right)\left(2-2\cos \beta \right)}=2P^2\sqrt{\left(1-\cos \alpha \right)\left(1-\cos \beta \right)}$.

Dany jest ostrosłup $ABCDS$, którego podstawą jest trapez prostokątny $ABCD$. Wysokością ostrosłupa jest krawędź $AS$. Wiedząc, że $AB\parallel CD$, $AB\perp AD$, $\left|AD\right|=\left|DC\right|=10$ i $\left|AB\right|=\left|AS\right|=20$ wyznaczymy stosunek pola ściany bocznej $BSC$ do pola podstawy ostrosłupa.

Rozwiązanie:

Wykonajmy rysunek pomocniczy:

R17w3MfxZs91z

Ilustracja przedstawia ostrosłup, którego podstawą jest trapez prostokątny A B C D. Kąty DAE oraz ADC to kąty proste. W podstawie zaznaczono jej wysokość opuszczoną z wierzchołka C na podstawę AB, spodek tej wysokości podpisano literą E. Odcinek AE ma długość 20, odcinek EB ma długość 10, krótsza podstawa trapezu CD ma długość dziesięć. Wysokość CE oraz prostopadłe ramię AD mają długość dziesięć. Wierzchołek górny ostrosłupa podpisano literą S. Krawędź boczna AS ma długość dwadzieścia.

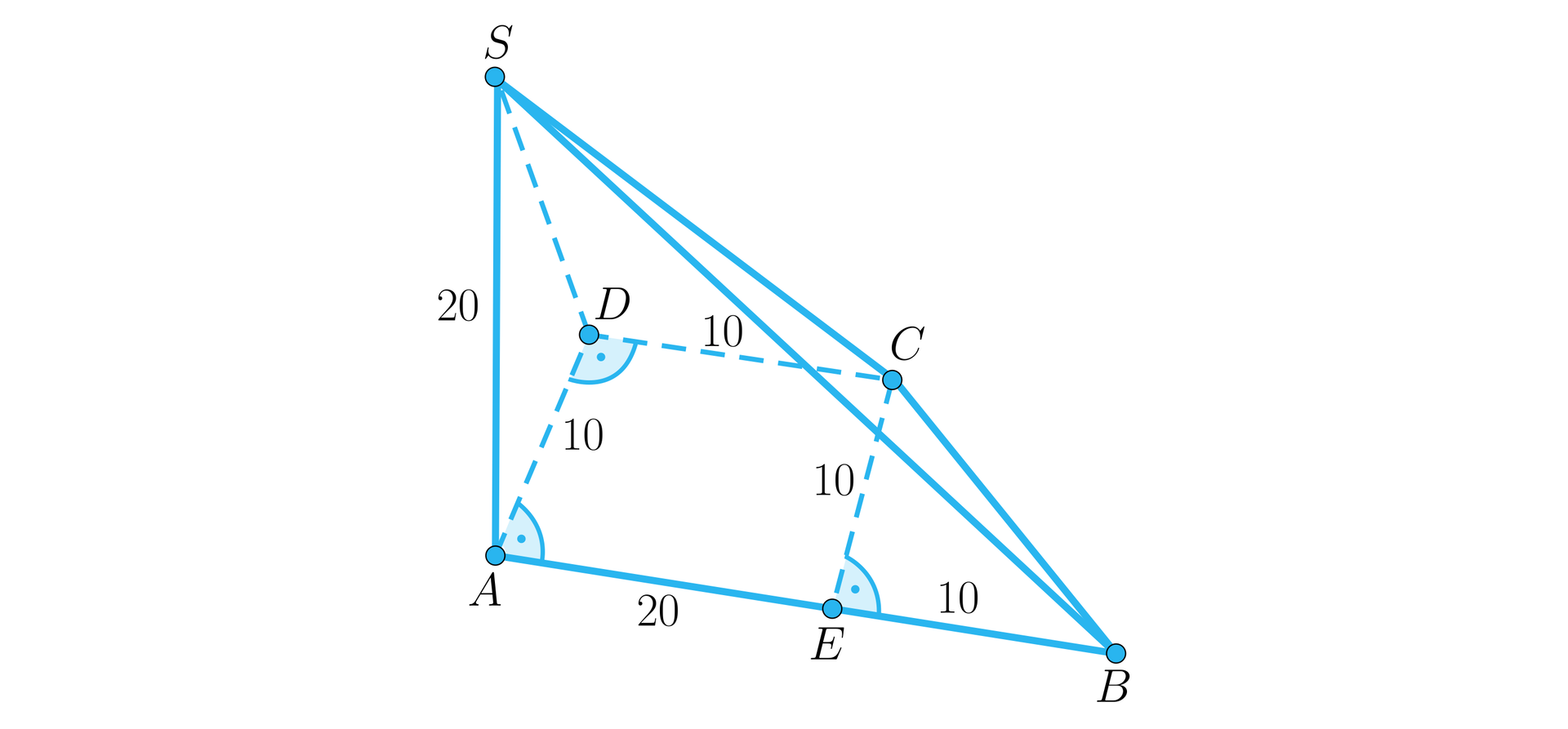
Zauważmy, że $\left|BC\right|=10\sqrt{2}$.

Trójkąty $SAD$ i $SAB$ są prostokątne, więc na mocy twierdzenia Pitagorasa mamy:

${20}^2+{10}^2={\left|SD\right|}^2$

$\left|SD\right|=\sqrt{500}=10\sqrt{5}$.

Analogicznie:

${20}^2+{20}^2={\left|SB\right|}^2$

$\left|SB\right|=20\sqrt{2}$.

RtroEk0TQxCbL

Ilustracja przedstawia ostrosłup, którego podstawą jest trapez prostokątny A B C D. Kąty DAE oraz ADC to kąty proste. W podstawie zaznaczono jej wysokość opuszczoną z wierzchołka C na podstawę AB, spodek tej wysokości podpisano literą E. Odcinek AE ma długość 20, odcinek EB ma długość 10, krótsza podstawa trapezu CD ma długość dziesięć. Wysokość CE oraz prostopadłe ramię AD mają długość dziesięć. W podstawie zaznaczono również przekątną AC. Wierzchołek górny ostrosłupa podpisano literą S. Krawędź boczna AS ma długość dwadzieścia.

Zauważmy, że trójkąt $SAC$ także jest prostokątny. $\left|AC\right|=10\sqrt{2}$. Zatem:

${20}^2+{\left(10\sqrt{2}\right)}^2={\left|SC\right|}^2$

$\left|SC\right|=\sqrt{600}=10\sqrt{6}$.

Możemy już obliczyć pole ściany $BSC$. Sprawdźmy, czy nie jest prostokątny.

${\left(10\sqrt{6}\right)}^2+{\left(10\sqrt{2}\right)}^2={\left(20\sqrt{2}\right)}^2$

$600+200=800$

$800=800$.

Trójkąt jest więc prostokątny.

$P_{BSC}=\frac{1}{2}·10\sqrt{6}·10\sqrt{2}=50\sqrt{12}=100\sqrt{3}$

Natomiast pole podstawy wynosi:

$P_p=\frac{\left(20+10\right)}{2}·10=150$.

Stosunek pola ściany bocznej $BSC$ do pola podstawy ostrosłupa wynosi więc:

$\frac{100\sqrt{3}}{150}=\frac{2\sqrt{3}}{3}$.

w podstawie ma czworokąt  a spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie.

Jedna z własności ostrosłupa prostego:  wszystkie krawędzie boczne są tej samej długości

w podstawie ma czworokąt, a jego wysokość nie spada na środek okręgu opisanego na podstawie.

Jedna z własności ostrosłupa pochyłego: krawędzie boczne nie są tej samej długości

ostrosłup prosty, którego podstawą jest kwadrat

kąt pomiędzy ramionami trójkąta równoramiennego będącego jego ścianą boczną

suma pól wszystkich ścian ostrosłupa