Przeczytaj
W tym materiale skupimy się na obliczaniu objętości ostrosłupa trójkątnego.
Ostrosłup trójkątny, to taki ostrosłup, którego podstawą jest trójkąt. Ściany boczne ostrosłupa są trójkątami o wspólnym wierzchołku zwanym wierzchołkiem ostrosłupa.
Ostrosłup trójkątny jest inaczej nazywany czworościanem.
Wśród ostrosłupów trójkątnych możemy wyróżnić ostrosłupy:
proste,
pochyłe.
Ostrosłup trójkątnyOstrosłup trójkątny nazywamy ostrosłupemostrosłupem prostym, jeśli spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie. Ostrosłup prosty ma wszystkie krawędzie boczne równej długości.
Ostrosłup trójkątny pochyły nie spełnia opisanej powyżej własności.
Jeśli wszystkie krawędzie boczne ostrosłupa tworzą z podstawą kąty równej miary, to spodek wysokości jest jednakowo oddalony od wierzchołków podstawy jest, więc środkiem okręgu opisanego na podstawie.
Jeśli wszystkie ściany boczne tworzą z podstawą kąty równej miary, to spodek wysokościspodek wysokości jest jednakowo oddalony od krawędzi podstawy. Jest więc środkiem okręgu wpisanego w podstawę.
Objętość ostrosłupa wyraża się za pomocą wzoru:
gdzie:
– oznacza pole podstawy ostrosłupa,
– wysokość bryły.
Dla czworościanu foremnegoczworościanu foremnego o krawędzi :
Objętość:
Zależność objętości ostrosłupa trójkątnego od objętości graniastosłupa
Zapoznaj się z poniższym apletem. Zauważ jak zmienia się objętość ostrosłupa trójkątnego względem objętości graniastosłupa (sześcianu). Przesuwając punkt lub zmieniasz długość krawędzi podstawy, gdy przesuniesz punkt zmieniasz wysokość ostrosłupa oraz graniastosłupa. Czy zauważasz związek miedzy objętościami tych brył?
Zapoznaj się z opisem poniższego apletu. Na podstawie opisanych przykładów przeanalizuj jak zmienia się objętość ostrosłupa trójkątnego względem objętości graniastosłupa (sześcianu). Czy zauważasz związek miedzy objętościami tych brył?
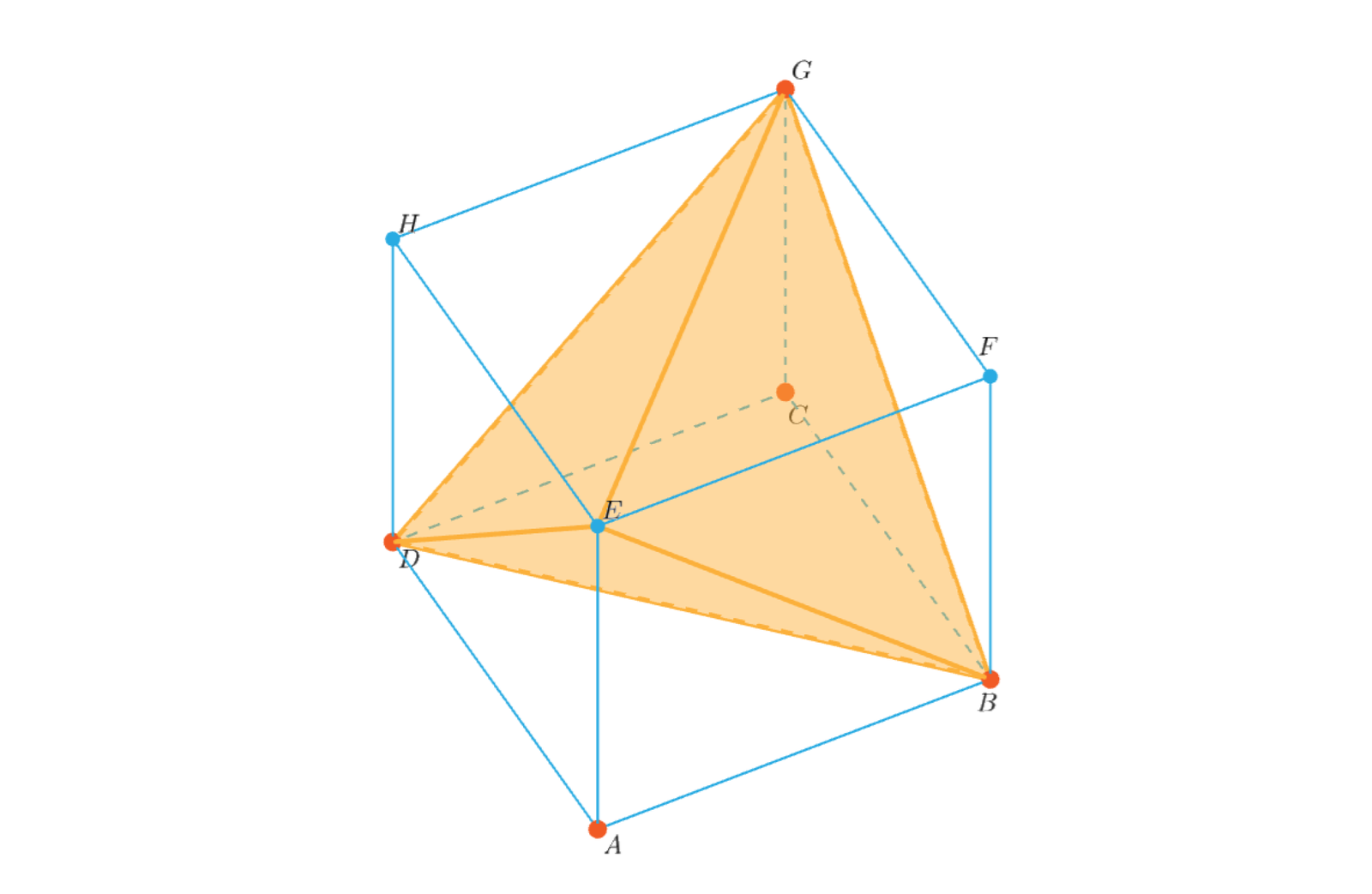
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DEey9jBxa
Pamiętaj, że objętość ostrosłupa jest jedną trzecią objętości graniastosłupa o tym samym polu podstawy oraz wysokości.
Obliczymy objętość ostrosłupa, którego podstawą jest trójkąt prostokątny równoramienny o przyprostokątnych długości 8, a krawędzie boczne są równe i tworzą z podstawą kąt o mierze .
Rozwiązanie
Zasadniczym elementem zadania jest ustalenie, gdzie znajduje się spodek wysokości ostrosłupa.
Wiemy, że ostrosłup ma krawędzie boczne równej długości, więc spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie.
W tym przypadku jest to środek przeciwprostokątnej, bo podstawą jest trójkąt prostokątny.
Wykonujemy rysunek z odpowiednimi oznaczeniami.
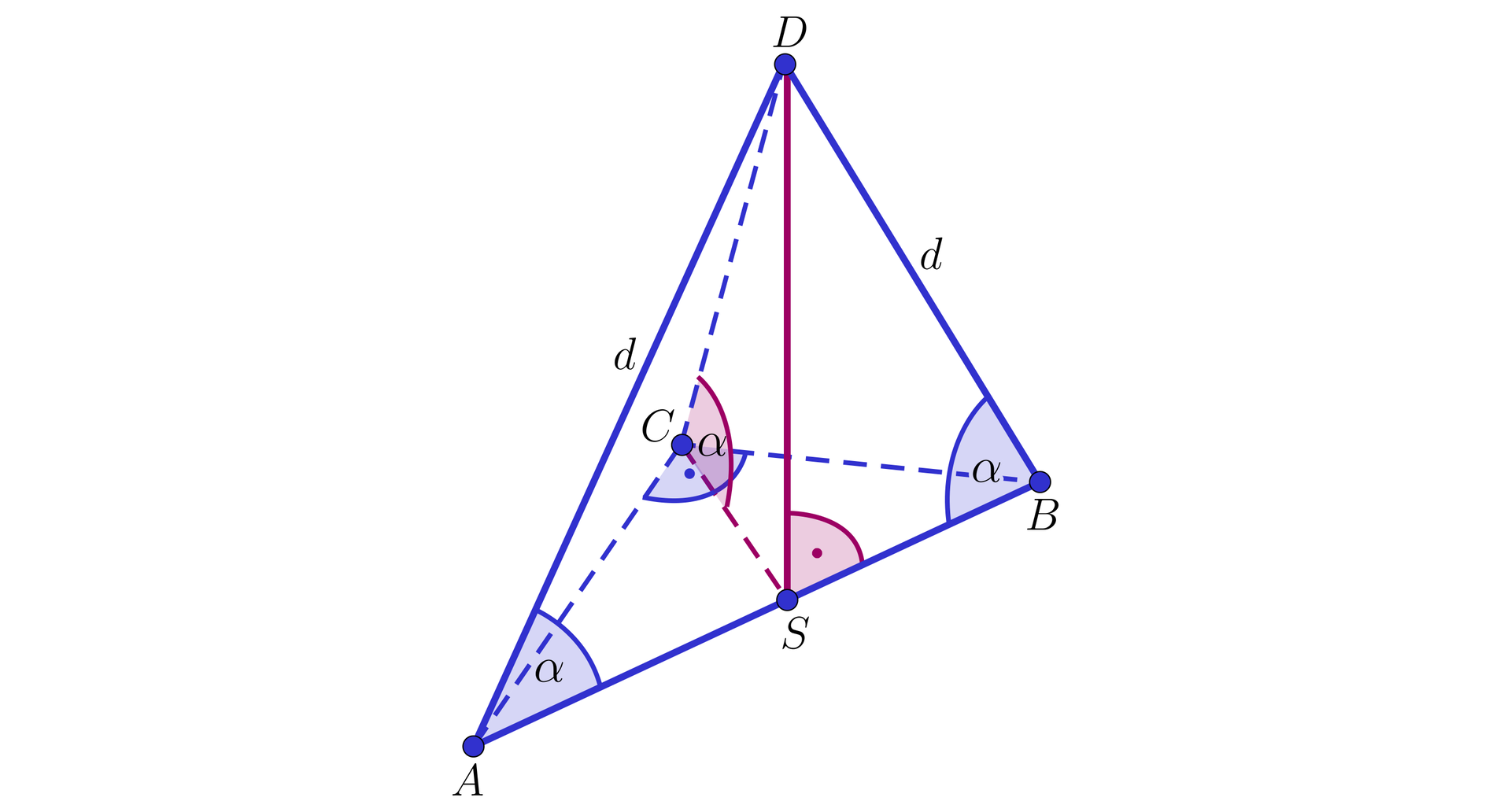
Wiemy, że są długościami ramion trójkąta prostokątnego w podstawie, więc .
Oznaczamy , bo z treści zadania wynika, że w ostrosłupie prostym krawędzie boczne są równej długości, miara kąta .
Wysokość ostrosłupa to odcinek , oznaczamy .
Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem , stad wniosek, że trójkąt jest równoboczny i .
Wysokość ostrosłupa jest wysokością ściany bocznej , zatem:
Obliczamy pole podstawy ostrosłupa:
Mamy już pole podstawy, możemy obliczyć objętość ostrosłupa:
.
Podstawą ostrosłupa jest trójkąt , a krawędź jest wysokością ostrosłupa. Oblicz objętość ostrosłupa , jeśli wiadomo, że , i pole jednej ściany bocznej prostopadłej do podstawy wynosi . Podaj wszystkie możliwe odpowiedzi.
Rozwiązanie
Wykonujemy rysunek z odpowiednimi oznaczeniami.
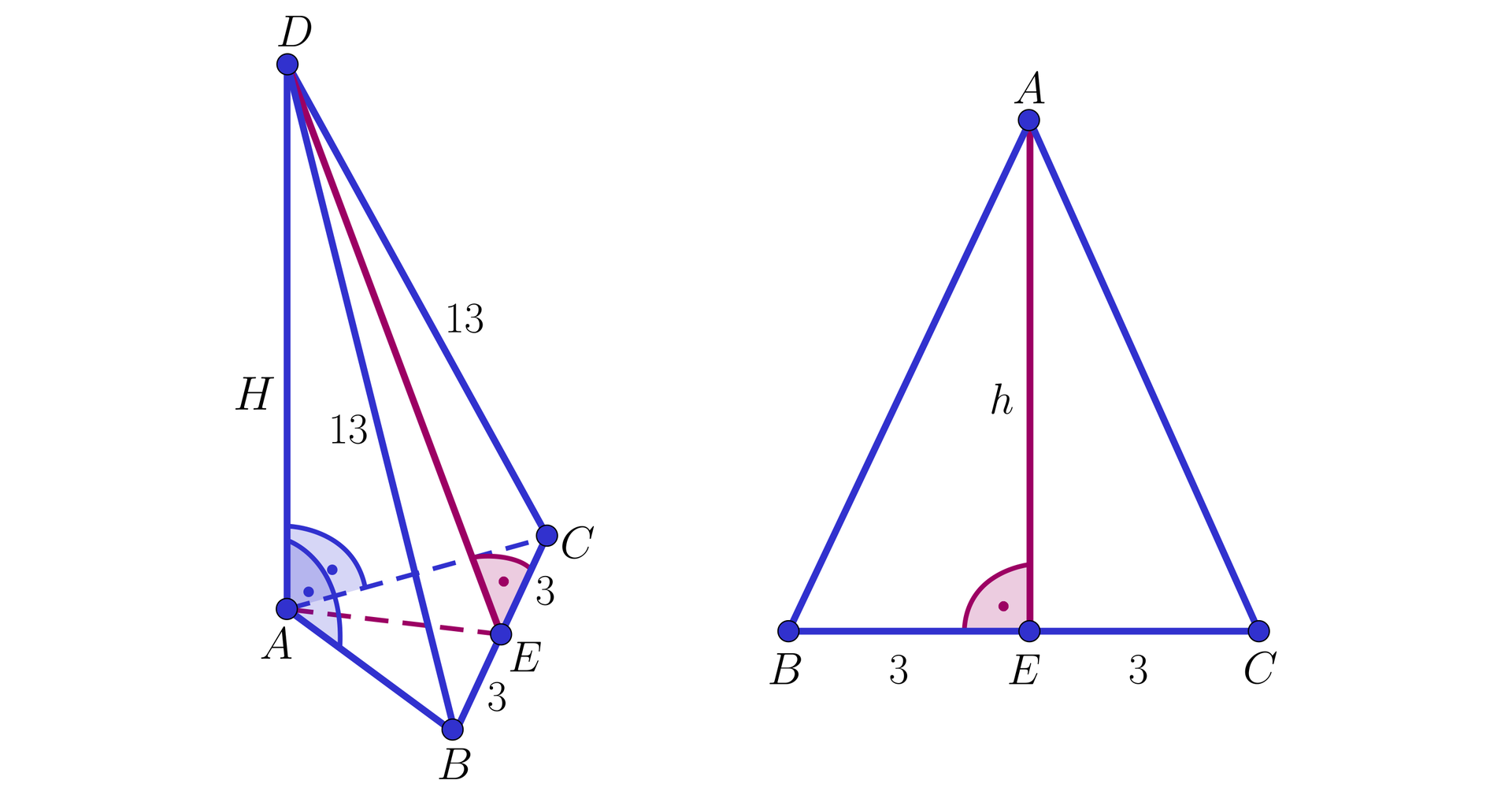
Oznaczymy długość wysokości ostrosłupa przez , z przystających trójkątów prostokątnych i na podstawie twierdzenia Pitagorasa mamy:
Zauważmy, że trójkąt jest równoramienny i oznaczamy długość jego wysokości .
Na podstawie twierdzenia Pitagorasa dla trójkąta mamy:
Możemy teraz wykorzystać podane pole ściany bocznej ostrosłupa.
Podnosząc obie strony do kwadratu mamy:
Otrzymaliśmy równanie dwukwadratowe, więc podstawmy , gdzie
lub
Stąd wyznaczamy lub bo , mamy więc dwa rozwiązania.
Należy teraz obliczyć pole podstawy i objętość ostrosłupa w każdym z przypadków.
Przypadek dla .
Obliczamy pole podstawy:
Obliczamy objętość ostrosłupa:
Przypadek dla .
Obliczamy pole podstawy:
Obliczamy objętość ostrosłupa:
Odpowiedź:
lub .
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę . Oblicz objętość tego ostrosłupa.
Rozwiązanie
Wykonujemy rysunek z odpowiednimi oznaczeniami.
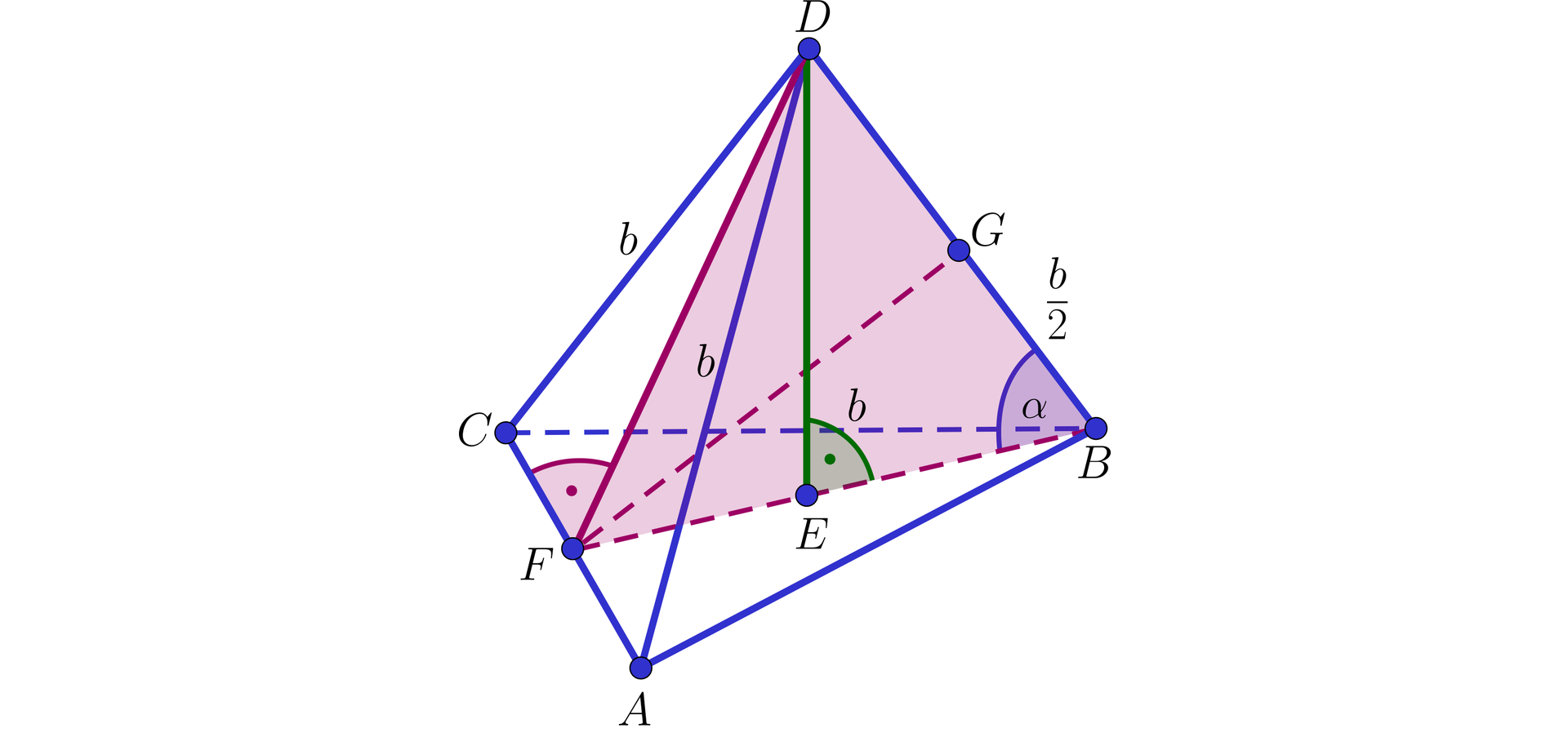
Korzystając z trójkąta możemy obliczyć wysokość ostrosłupa
to
Zauważmy, że trójkąty i są przystające.
Zatem i trójkąt jest równoramienny, stąd punkt jest środkiem odcinka .
Z trójkąta mamy:
to
Teraz z trójkąta prostokątnego obliczamy długość odcinka .
Zatem objętość jest równa
Odpowiedź:
.
Słownik
ostrosłup, którego podstawą jest wielokąt foremny i spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie
rzut prostokątny wierzchołka bryły na płaszczyznę podstawy
ostrosłup prosty, którego podstawą jest trójkąt równoboczny
ostrosłup prawidłowy trójkątny, którego wszystkie cztery ściany są trójkątami równobocznymi