Symulacja interaktywna

Polecenie 1

Zapoznaj się z poniższą symulacją interaktywną. Zauważ jak zmienia się objętość ostrosłupa trójkątnego, gdy zmienia się krawędź podstawy lub wysokość ostrosłupa. Użyj suwaków, by zmienić długość krawędzi podstawy a i wysokość H ostrosłupa.

Zapoznaj się z opisem poniższej symulacji interaktywnej. Na podstawie opisanych przykładów zastanów się jak zmienia się objętość ostrosłupa trójkątnego, gdy zmienia się krawędź podstawy lub wysokość ostrosłupa.

R1Eiss6pSzF23
Na symulacji przedstawiono ostrosłup trójkątny ABCD. W podstawie znajduje się trójkąt prostokątny, równoramienny. Krawędź boczna AD stanowi wysokość ostrosłupa. Linią przerywaną zaznaczono wysokość AE podstawy oraz wysokość DE ściany bocznej. Literą a oznaczono długość krawędzi AB i AC. Można zmieniać wartość długości krawędzi a oraz wysokości H. Poniżej wyświetla się objętość ostrosłupa, wyliczana dla zadanych wartości a i H. Przykład pierwszy. Gdy a, równa się, cztery oraz H, równa się, dwa. Objętość ostrosłupa wynosi pięć i trzydzieści trzy setne. Przykład 2. Gdy a, równa się, dwa oraz H, równa się, jeden, objętość ostrosłupa wynosi sześćdziesiąt siedem setnych. Przykład 3. Gdy a, równa się, pięć, oraz H, równa się, pięć, objętość ostrosłupa wynosi dwadzieścia i osiemdziesiąt trzy setne.

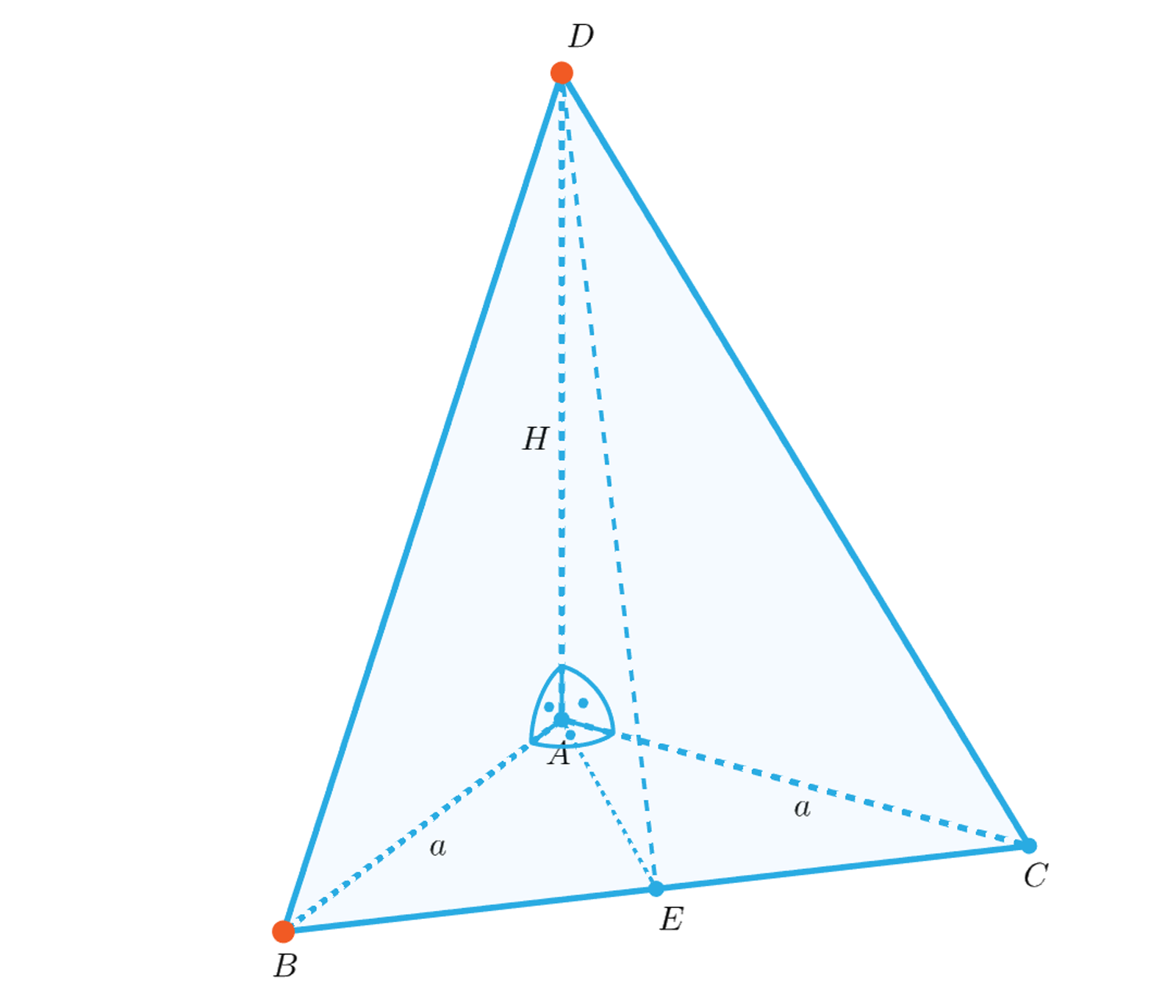
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DKsZWJ0TK

Polecenie 2

Oblicz objętość ostrosłupa z rysunku, gdy AB=4, wysokość AD=5. Wiedząc, że w podstawie jest trójkąt prostokątny równoramienny.

Rzn5F7C0uBUJW
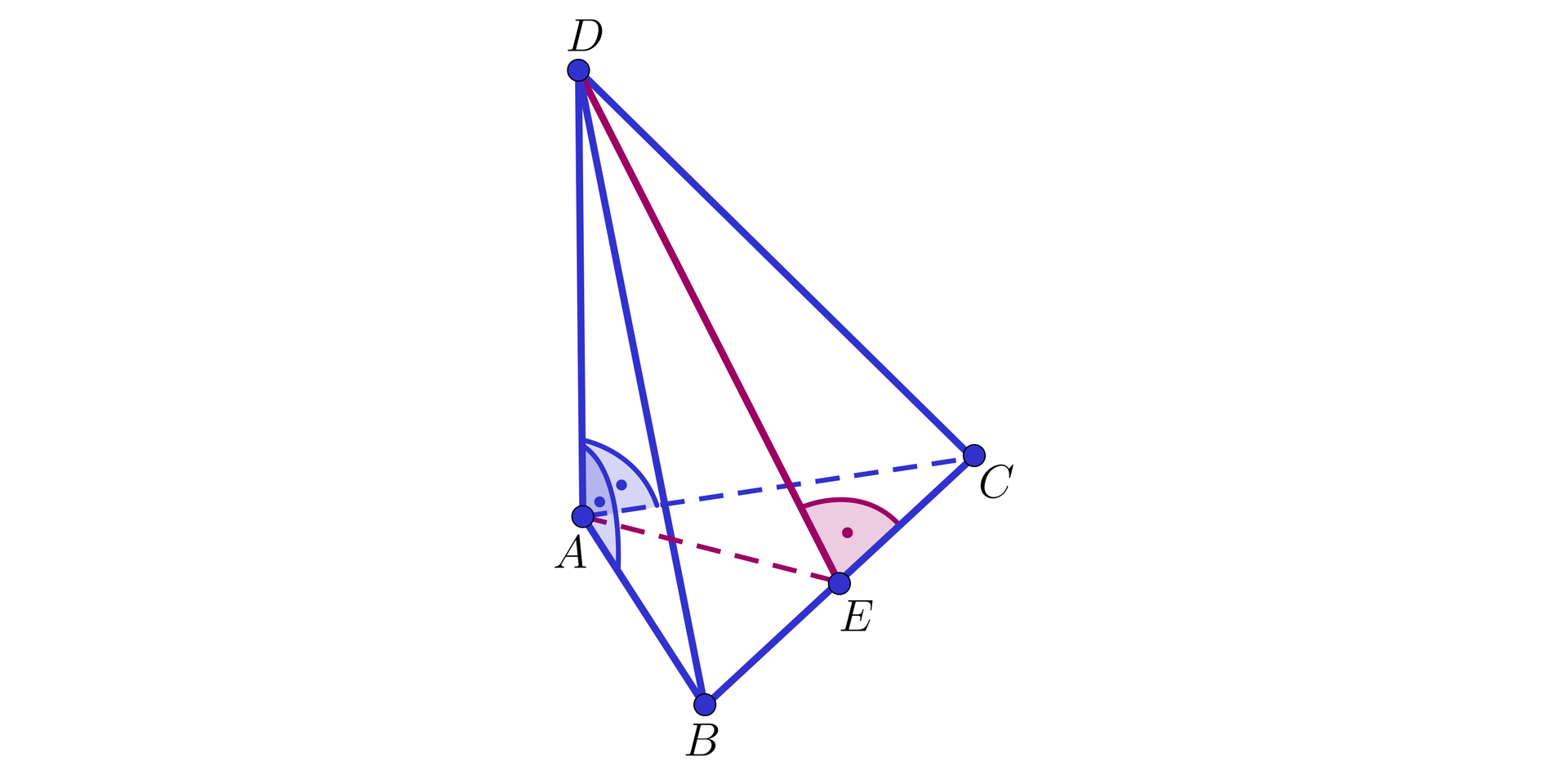
Na ilustracji przedstawiono ostrosłup ABCD. W podstawie ostrosłupa znajduje się trójkąt prostokątny równoramienny. Z wierzchołka D opuszczono wysokość ściany bocznej, której spodek leży w punkcie E na krawędzi BC. Linią przerywaną połączono wierzchołek A z punktem E. Ściany boczne ABD oraz ACD stanowią trójkąty prostokątne.
Polecenie 3

Ustaw w symulacji punkt D tak, aby odcinek H zwiększył się dwukrotnie oraz punkt A tak, aby krawędź podstawy zwiększyła się dwukrotnie. Oblicz, jaką częścią objętości pierwotnej jest objętość ostrosłupa po zmianie.

Jak zmieni się objętość ostrosłupa trójkątnego, który w podstawie ma trójkąt prostokątny równoramienny, jeżeli zwiększymy długość tego ramienia i wysokość bryły dwukrotnie?

Przeczytaj
Sprawdź się