Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Dwie sąsiednie ściany ostrosłupa trójkątnego są prostopadłe. Ich wspólna krawędź ma długość $b$ , zaś wysokości tych ścian opuszczone na wspólną krawędź są równe $a$ oraz $c$ , jak na rysunku.

RxLU7CFax4NFN

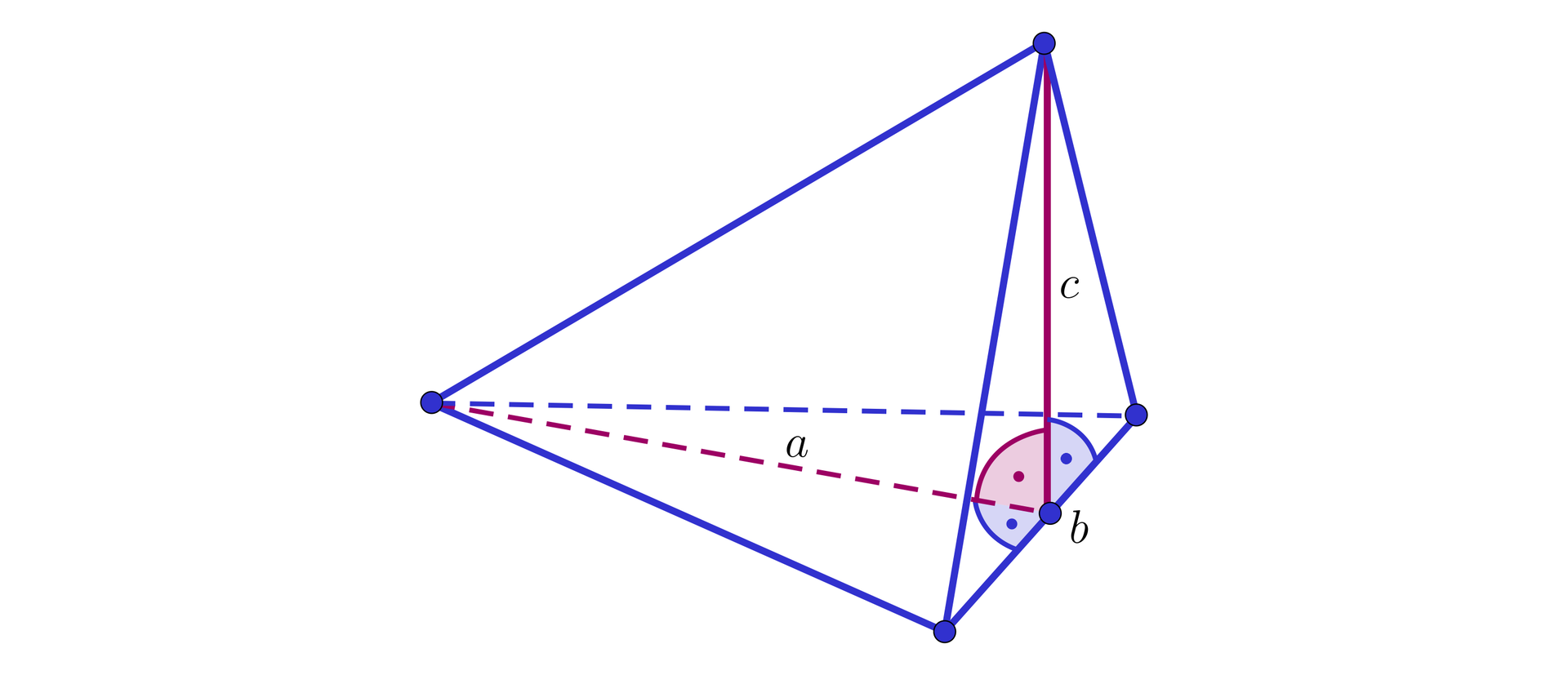
Na ilustracji przedstawiono ostrosłup ABCD. Z wierzchołka D opuszczono wysokość ściany bocznej, oznaczoną literą c. Wysokość ta jest prostopadła do płaszczyzny podstawy. Krawędź BC trójkąta w podstawie oznaczono literą b. Linią przerywaną zaznaczono wysokość podstawy poprowadzoną z wierzchołka A na bok B C i oznaczono ją literą a.

RDI3JjAz8iFsB

RCEG6dAJUyabL1

Ćwiczenie 2

R1XCy4cWikDv72

Ćwiczenie 3

R15hZ92KwuknC2

Ćwiczenie 4

R1Won02nPwqtv2

Ćwiczenie 5

R1971zYAxcX992

Ćwiczenie 6

Rejva0xoQztwb2

Ćwiczenie 7

R1PUHUrtyfpyw3

Ćwiczenie 8

Ćwiczenie 9

Podstawą ostrosłupa $A B C D$ jest trójkąt równoramienny o podstawie $|A B| = b$ i kącie $α$ pomiędzy ramionami. Krawędź $C D$ jest wysokością ostrosłupa, a kąt nachylenia ściany $A B D$ do podstawy ostrosłupa jest równy $β$ . Oblicz objętość tego ostrosłupa.

REGq27qfVVgbq

Na ilustracji przedstawiono ostrosłup ABCD. Krawędź boczna CD stanowi wysokość ostrosłupa i oznaczono ją literą H. Na krawędzi AB podstawy zaznaczono punkt E, który stanowi spodek wysokości podstawy opuszczonej z wierzchołka C. Linią przerywaną zaznaczono wysokość DE ściany bocznej i oznaczono literą h. ∢CED oznaczono beta, natomiast ∢BCA oznaczono alfa. ∢DCB jest kątem prostym.

W trójkącie prostokątnym $A C E$ mamy:

$\frac{|A E|}{|C E|} = tg \frac{α}{2}$ stąd $|C E| = \frac{\frac{b}{2}}{tg \frac{α}{2}} = \frac{b}{2 tg \frac{α}{2}}$ oraz

$\frac{|A E|}{|C A|} = \sin \frac{α}{2}$ stąd $|C A| = \frac{\frac{b}{2}}{\sin \frac{α}{2}} = \frac{b}{2 \sin \frac{α}{2}}$

Obliczamy pole podstawy ostrosłupa:

$P_{p} = \frac{1}{2} \cdot |A B| \cdot |C E| = \frac{1}{2} \cdot b \cdot \frac{b}{2 tg \frac{α}{2}} = \frac{b^{2}}{4 tg \frac{α}{2}}$

Z trójkąta prostokątnego $D C E$ mamy:

$\frac{|D C|}{|C E|} = tg β$ stąd $|D C| = |C E| \cdot tg β = \frac{b}{2 tg \frac{α}{2}} \cdot tg β = \frac{b tg β}{2 tg \frac{α}{2}}$

Możemy obliczyć objętość:

$V = \frac{1}{3} \cdot P_{p} \cdot H = \frac{1}{3} \cdot \frac{b^{2}}{4 tg \frac{α}{2}} \cdot \frac{b tg β}{2 tg \frac{α}{2}} = \frac{b^{3} tg β}{24 {tg}^{2} \frac{α}{2}}$

$V = \frac{b^{3} tg β}{24 {tg}^{2} \frac{α}{2}}$ .

Symulacja interaktywna

Dla nauczyciela