Przeczytaj

Zacznijmy od przeanalizowania poniższej tabeli.

Wartości funkcji trygonometrycznych dla wybranych wielokrotności kąta $90 °$
Wartości kąta $α$ wyrażone w stopniach	Wartości kąta $α$ wyrażone w radianach	$\sin α$	$\cos α$	$tg α$
$0 °$	$0$	$0$	$1$	$0$
$90 °$	$\frac{π}{2}$	$1$	$0$	nie istnieje
$180 °$	$π$	$0$	$- 1$	$0$
$270 °$	$\frac{3 π}{2}$	$- 1$	$0$	nie istnieje
$360 °$	$2 π$	$0$	$1$	$0$
$- 90 °$	$- \frac{π}{2}$	$- 1$	$0$	nie istnieje
$- 180 °$	$- π$	$0$	$- 1$	$0$
$- 270 °$	$- \frac{3 π}{2}$	$1$	$0$	nie istnieje

Już pobieżna obserwacja wartości funkcji trygonometrycznych opisywanych w tej tabeli pozwala wywnioskować istnienie pewnych zależności między nimi, a także pewnej regularności w przyjmowanych wartościach. Oczywiście jest ona efektem okresowościfunkcja okresowaokresowości każdej z tych funkcji – wartości przyjmowane przez każdą z tych funkcji powtarzają się, gdy zwiększymy argument o wielokrotność okresu. Dla sinusa i cosinusa okres ten wynosi $360 °$ , zaś dla tangensa $180 °$ . Dzięki temu znając wartości funkcji trygonometrycznych dla całkowitych wielokrotności kąta $90 °$ z przedziału $⟨0 °, 360 °⟩$ , jesteśmy w stanie ustalić ich wartość dla dowolnej całkowitych wielokrotności kąta $90 °$ .

Skupmy się początkowo na funkcjach sinus i cosinus. Wartości przyjmowane przez każdą z nich dla wymienionych w tabeli kątów należą do trójelementowego zbioru $\{- 1, 0, 1\}$ . Przypomnijmy wykresy tych dwóch funkcji.

RaCm6PNagkH6Z

Ilustracja przedstawia wykresy funkcji sinus x i cosinus x. Sinus x zaczyna się w zerze, osiąga 1 w pi przez dwa, 0 w argumencie pi i minus jeden w trzy drugie pi. Wykres cosinusa zaczyna się w jedynce, osiąga wartość 0 w pi przez dwa, potem minus jeden w argumencie pi i jeden w argumencie dwa pi. Wykresy powtarzają się co dwa pi.

Wykresy funkcji sinus i cosinus. Dla czytelności przerywanymi liniami narysowano proste $y = 1$ i $y = - 1$ .

Funkcja tangens znacznie się różni od poprzednich dwóch funkcji trygonometrycznych. Z tabeli możemy odczytać, że dla parzystych wielokrotności kąta $90 °$ przyjmuje wartość $0$ , zaś dla nieparzystych wielokrotności kąta $90 °$ nie istnieje. Te same wnioski można wyciągnąć z wykresu funkcji tangens.

RTCLtL8CWHS08

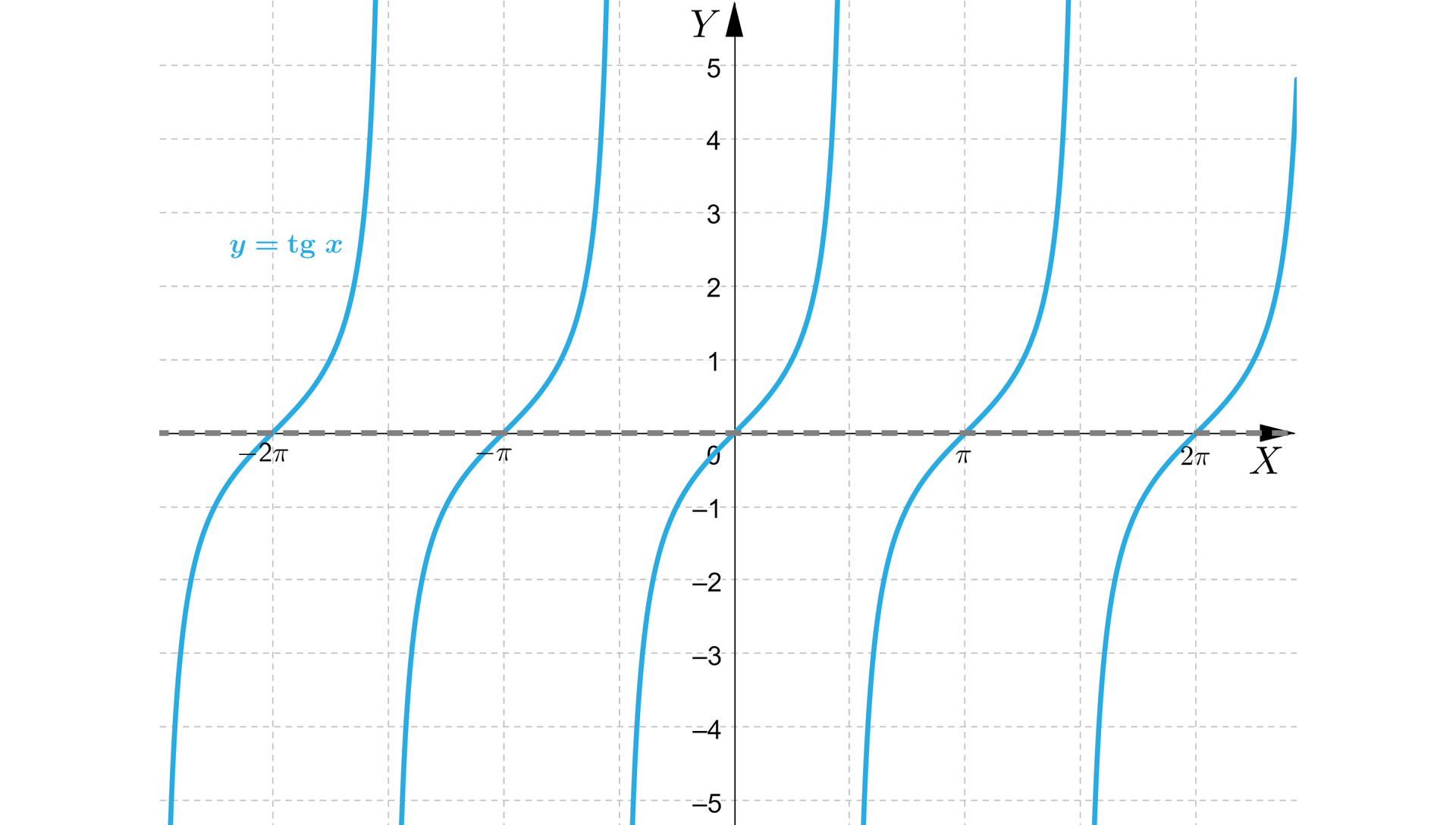
Ilustracja przedstawia wykres funkcji tanges x, dla argumentu 0 przyjmuję ona wartość 0, dla jedynki zbliża się do plus nieskończoności, a dla minus jedynki do minus nieskończoności. Okres tej funkcji powtarza się co pi.

Wykres funkcji tangens. Dla czytelności przerywaną linią zaznaczono prostą $y = 0$ .

Spróbujmy teraz sformułować zaobserwowane własności w postaci wzorów na wartości funkcji trygonometrycznych całkowitych wielokrotności kąta $90 °$ . Dla dowolnej liczby całkowitej $k$ mamy:

$\sin k π = \cos (\frac{π}{2} + k π) = tg k π = 0$ ;

$\sin (\frac{π}{2} + 2 k π) = \cos 2 k π = 1$ ;

$\sin (\frac{3 π}{2} + 2 k π) = \cos (2 k + 1) π = - 1$ ;

$tg (\frac{π}{2} + k π)$ – nie istnieje.

Postarajmy się zastosować owe wzory w zadaniach. Zacznijmy od bezpośredniego wykorzystania uzyskanych wzorów.

Przykład 1

Spróbujemy wyznaczyć następujące wartości funkcji trygonometrycznych:

$\sin 540 °$ ;
$\cos 270 °$ ;
$tg (- 90 °)$ .

Rozwiązanie:

Zaczynając od pierwszego z obliczanych wyrażeń:

$\sin 540 ° = \sin (3 \cdot 180 °) = 0$

W drugim przypadku jesteśmy w stanie wyczytać wartość funkcji z omawianej uprzednio tabelki.

$\cos 270 ° = \cos \frac{3 π}{2} = \cos (\frac{π}{2} + π) = 0$

Podobnie jest w ostatnim przypadku, z tą różnicą, że szukana przez nas wartość $tg (- 90 °) = tg (\frac{π}{2} - π)$ nie istnieje.

Czasami zmuszeni jesteśmy wykorzystywać znajomość wartości funkcji trygonometrycznych wielokrotności kąta prostego.

Przykład 2

Oblicz wartość wyrażenia $\frac{\sin 1350 ° \cdot \sin 8730 °}{\cos 11340 °}$ .

Rozwiązanie:

$\frac{\sin 1350 ° \cdot \sin 8730 °}{\cos 11340 °} = \frac{\sin \frac{15 π}{2} \cdot \sin \frac{97 π}{2}}{\cos 63 π} = \frac{\sin (\frac{3 π}{2} + 6 π) \cdot \sin (\frac{π}{2} + 48 π)}{\cos 63 π} = \frac{- 1}{- 1} = 1$

Przejdźmy do zadań, które wymagają od nas mniej bezpośredniego wykorzystania poznanych wartości.

Przykład 3

Wyznaczymy wszystkie wartości kąta $α$ , dla których spełnione jest równanie $\sin α + \sin (α + 90 °) \cdot \sin α = 0$ .

Rozwiązanie:

Wyłączając przed nawias wyrażenie $\sin α$ uzyskujemy:

$(1 + \sin (α + 90 °)) \cdot \sin α = 0$

Mamy więc do czynienia z sytuacją, gdzie iloczyn dwóch liczb rzeczywistych jest równy zero. Oznacza to, że co najmniej jeden z czynników jest zerem. Tak więc:

$1 + \sin (α + 90 °) = 0 \lor \sin α = 0$

Pierwsza równość z powyższej alternatywy po przekształceniu daje się zapisać jako:

$\sin (α + 90 °) = - 1$

Zauważmy, że podstawiając $x = α + 90 °$ uzyskujemy, że $\sin x = - 1$ . Wiemy, że dla całkowitych wartości $k$ zachodzi $\sin (\frac{3 π}{2} + 2 k π) = - 1$ . Zatem:

$x = α + \frac{π}{2} = \frac{3 π}{2} + 2 k π$ , skąd $α = (2 k + 1) π$ .

Rozważmy drugą z możliwości, tj. $\sin α = 0$ . Wiemy, że sinus dowolnej całkowitej wielokrotności kąta $π$ wynosi $0$ , tak więc z drugiej składowej alternatywy mamy $α = k π$ , gdzie $k$ jest pewną liczbą całkowitą.

Ostatecznie, dochodzimy do wniosku że $α \in \{k π : k \in ℤ\}$ (jako że zbiór rozwiązań drugiego równania obejmuje wszystkie rozwiązania z pierwszego).

Przykład 4

Rozwiążemy równanie $\frac{1 - \cos 4 x}{\sin x} = 0$ .

Rozwiązanie:

Zacznijmy od wyznaczenia dziedziny.

Oczywiście $\sin x \neq 0$ , więc $x \neq k π$ , gdze $k \in ℤ$ .

Przyrównując licznik do zera otrzymujemy równanie:

$1 - \cos 4 x = 0$ , więc

$4 x = 2 k π$ , czyli $x = \frac{1}{2} k π$ , gdze $k \in ℤ$ .

Uwzględniając założenia otrzymujemy rozwiązania:

$x = \frac{2 k + 1}{2} π$ , gdze $k \in ℤ$ .

Przykład 5

Rowzwiążemy równanie: $\sin^{2} (2 α + \frac{π}{2}) + \sin (2 α + \frac{π}{2}) = 0$

Rozwiązanie:

Wyłączając $\sin (2 α + \frac{π}{2})$ przed nawias otrzymujemy równanie:

$\sin (2 α + \frac{π}{2}) (\sin (2 α + \frac{π}{2}) + 1) = 0$ .

Zatem $\sin (2 α + \frac{π}{2}) = 0$ lub $\sin (2 α + \frac{π}{2}) = - 1$ , więc

$2 α + \frac{π}{2} = k π$ lub $2 α + \frac{π}{2} = - \frac{π}{2} + 2 k π$ .

Mamy zatem:

$2 α = - \frac{π}{2} + k π$ lub $2 α = - π + 2 k π$ .

Ostatecznie dostajemy dwie serie rozwiązań:

$α = - \frac{π}{4} + \frac{k}{2} π$ lub $α = - \frac{π}{2} + k π$ , gdzie $k \in ℤ$ .

Zauważmy, że w powyższym rozumowaniu wykorzystaliśmy obserwację niejako odwrotną do rozumowania stosowanego w poprzednich przykładach. Tym razem z faktu, że $\sin α = 0$ wywnioskowaliśmy, że $α$ jest wielokrotnością kąta $180 °$ . Warto mieć na uwadze, że nie jesteśmy w stanie wyznaczyć wartości tego kąta w sposób jednoznaczny bez dodatkowych informacji, gdyż funkcje trygonometryczne nie są różnowartościowefunkcja różnowartościowaróżnowartościowe.

Słownik

funkcja okresowa

funkcję $f : ℝ \to ℝ$ nazywamy okresową, jeżeli istnieje taka liczba $T > 0$ (nazywana okresem funkcji), że $f (x + T) = f (x)$ dla wszystkich $x \in ℝ$ . Funkcje trygonometryczne są przykładami funkcji okresowych

funkcja różnowartościowa

funkcję $f : ℝ \to ℝ$ nazwiemy różnowartościową, gdy dla różnych argumentów przyjmuje różne wartości, tzn. dla dowolnych $x, y \in ℝ$ takich, że $x \neq y$ zachodzi $f (x) \neq f (y)$ . Przykładem funkcji różnowartościowej jest funkcja identycznościowa $f (x) = x$

Wprowadzenie

Prezentacja multimedialna

Słownik