Przeczytaj
Zajmiemy się teraz odczytywaniem własności funkcjifunkcji z jej wykresu. Jest to zagadnienie wymagające dużej uwagi, o czym przekonać nas powinien następujący przykład.
Funkcja określona jest na zbiorze liczb rzeczywistych, a fragment jej wykresu dla argumentówargumentów należących do przedziału przedstawiony został poniżej.
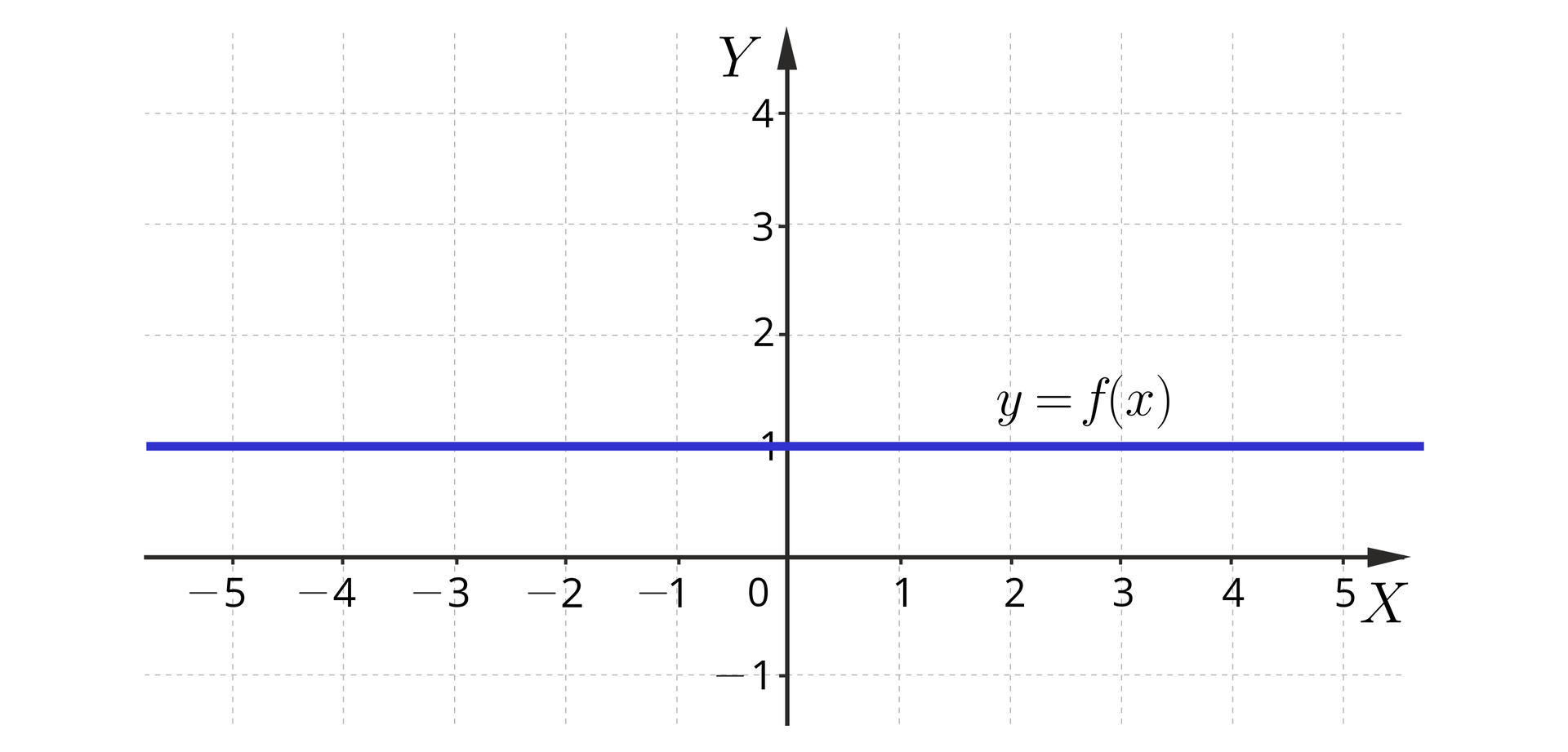
Może się nam wydawać, że o funkcji wiemy już wszystko.
I tak: „na pewno” jest ona stale równa . Otóż niekoniecznie! Zupełnie inną możliwość pokazuje poniższy rysunek, na którym przedstawiono znacznie większy fragment wykresu tej funkcji:
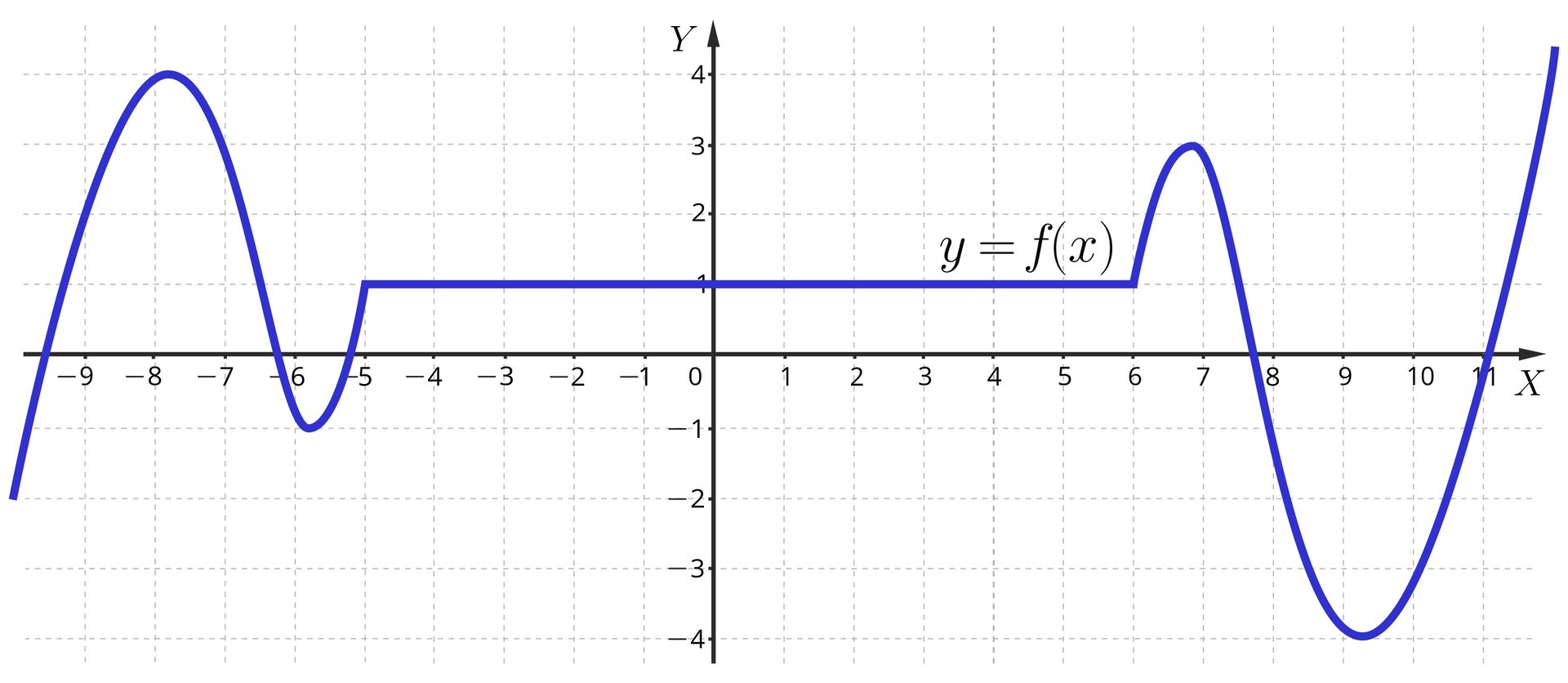
W tym materiale będziemy rozważać przede wszystkim funkcje określone na pewnym przedziale domkniętym, co pozwoli nam przedstawiać całe wykresy tych funkcji i uniknąć problemu z powyższego przykładu. Warto jednak pamiętać, że tak naprawdę zawsze przedstawiamy tylko rysunek wykresu, który nie jest idealny. Czytanie go może zatem być obarczone pewnym - niewielkim zazwyczaj - błędem.
Jeśli punkt na końcu krzywej nie należy do wykresu, to oznaczamy go kółkiem niezamalowanym, jeśli zaś punkt należy, to kółkiem zamalowanym. Na rysunku poniżej lewy koniec krzywej należy do wykresu, a prawy nie. W dalszym ciągu będziemy tę zasadę często stosować, ale jeśli fakt, czy końce należą, czy też nie należą do wykresu, będzie w danym kontekście mało istotny, zostawiać będziemy jego końce bez kółeczek.
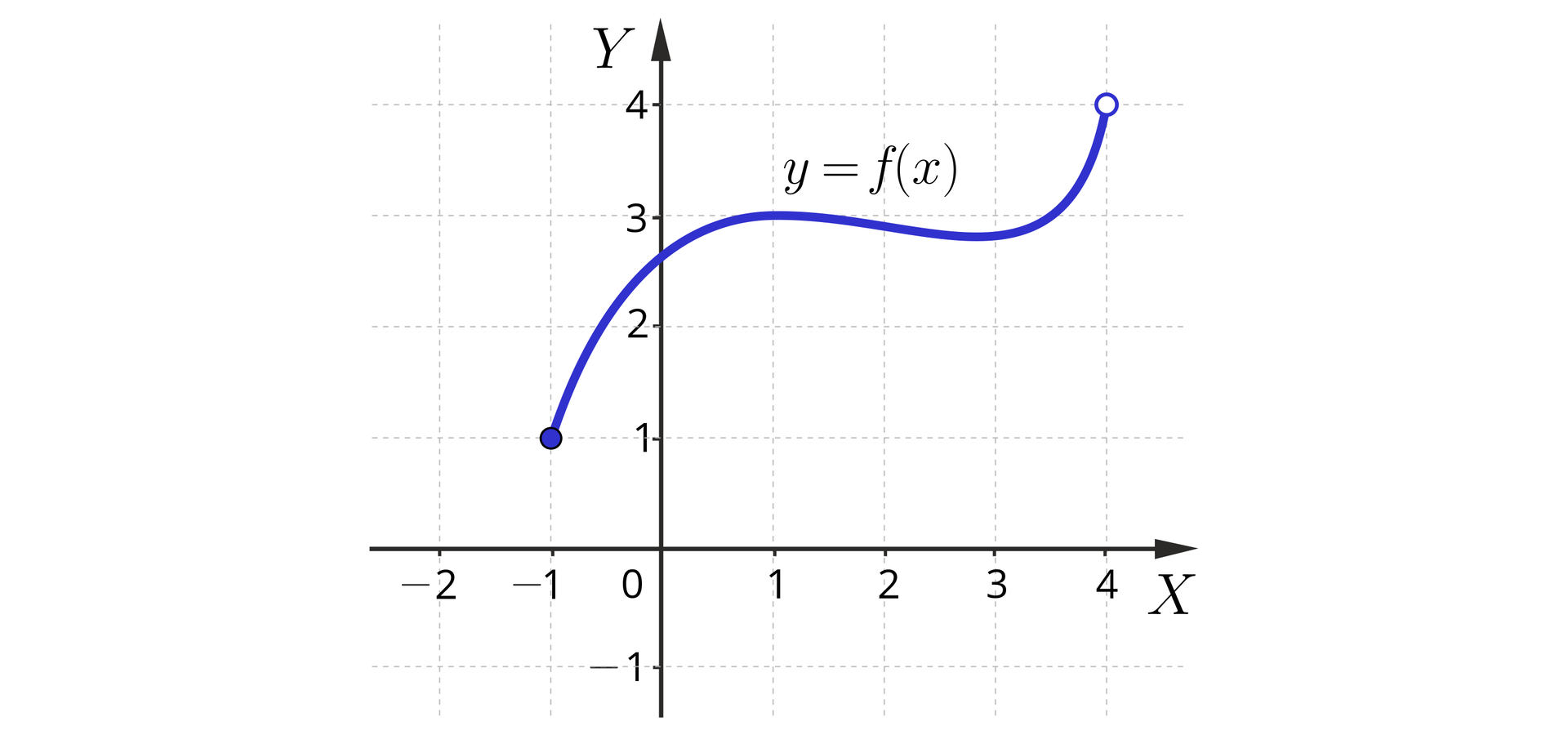
Na podstawie wykresu funkcji możemy odczytać m.in.:
dziedzinędziedzinę i zbiór wartości funkcjizbiór wartości funkcji, największą oraz najmniejszą wartość funkcji;
przedziały, w których funkcja wzrasta oraz w których maleje;
punkty, dla których funkcja osiąga wartość zero;
przedziały, w których funkcja przyjmuje wartości dodatnie i przedziały, w których przyjmuje wartości ujemne.
Przez największą wartość funkcji w danym przedziale domkniętym rozumiemy największą z tych liczb, które są wartościami funkcji dla argumentów z tego przedziału. Analogicznie definiujemy najmniejszą wartość.
Na podstawie wykresu funkcji znajdziemy jej:
a) dziedzinę,
b) zbiór wartości,
c) wartość największą,
d) wartość najmniejszą.
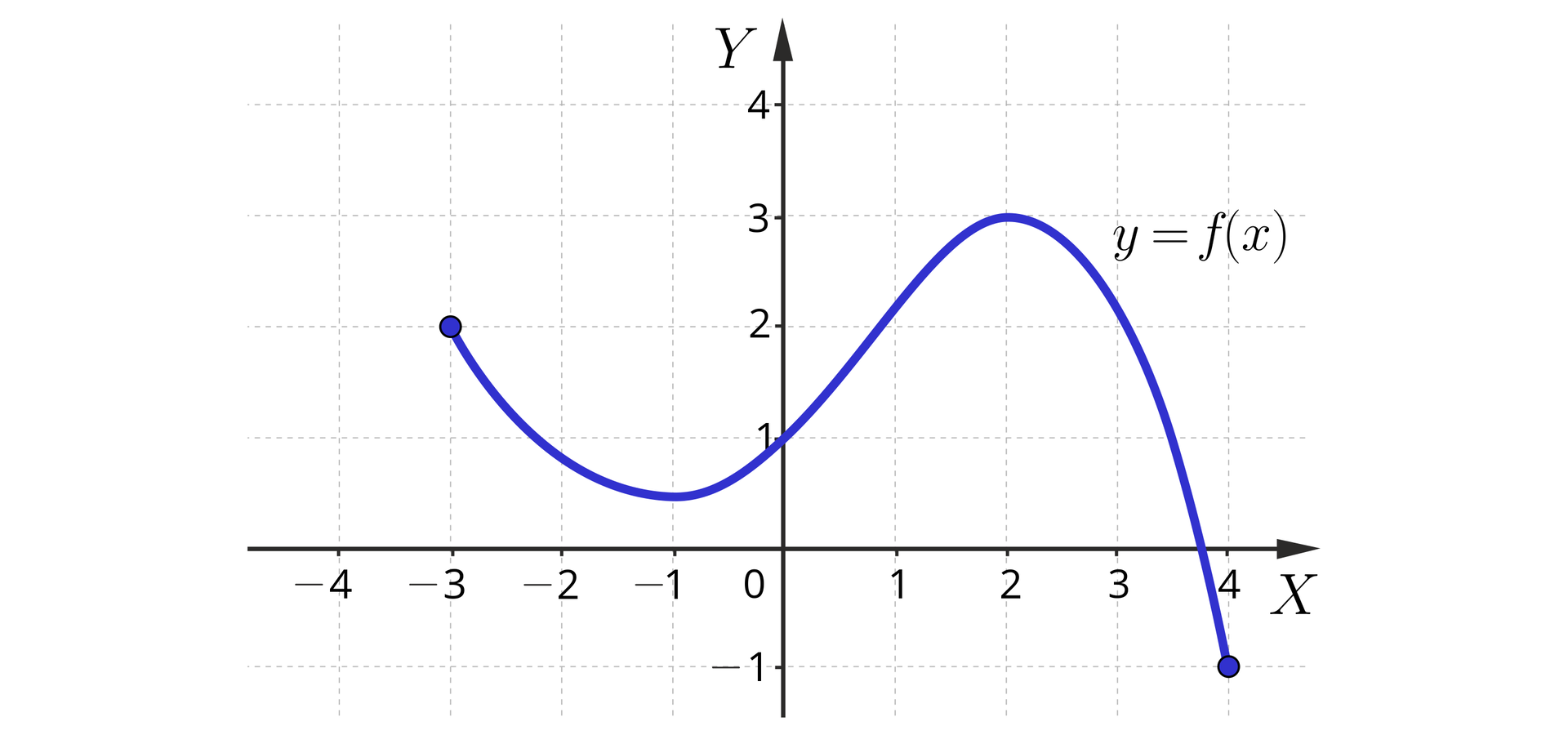
Rozwiązanie
Zauważamy, że:
a) dziedzina funkcji to . Aby się o tym przekonać, wystarczy zauważyć, że proste pionowe o równaniu przecinają wykres funkcji wtedy i tylko wtedy, gdy ;
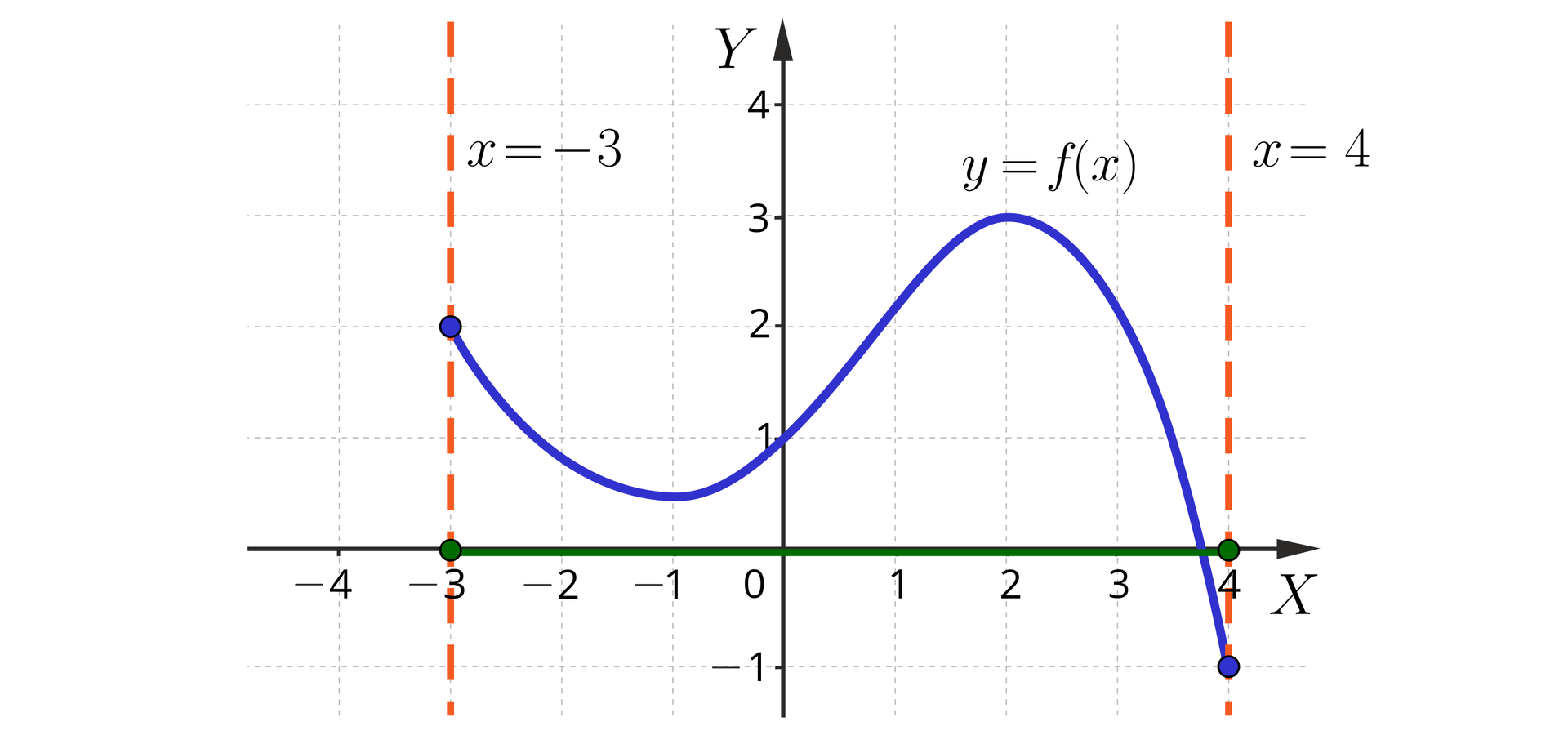
b) zbiorem wartości funkcji jest przedział . Aby się o tym przekonać, zauważmy, że zarówno prosta , jak i prosta ma jeden punkt wspólny z wykresem funkcji . Ponadto każda prosta pozioma, leżąca pomiędzy tymi dwiema prostymi, przecina wykres funkcji . Jednocześnie żadna prosta pozioma, leżąca ponad prostą , ani żadna prosta pozioma leżąca poniżej prostej nie przecinają go;
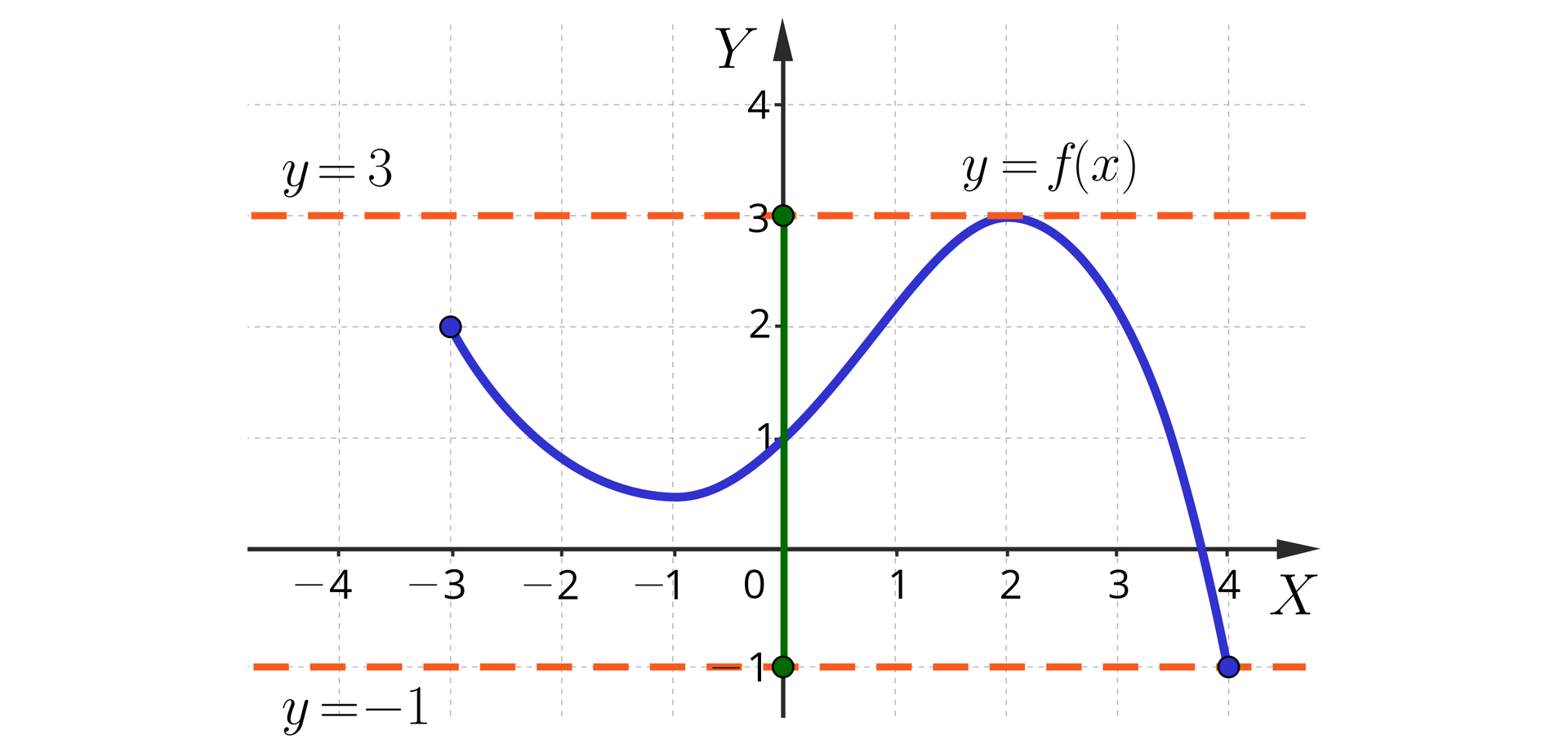
c) największą wartością funkcji jest liczba ;
d) najmniejszą wartością funkcji jest liczba .
Wykres funkcji jest pokazany na poniższym rysunku. Znajdziemy:
a) miejsca zerowe funkcjimiejsca zerowe funkcji ;
b) argumenty, dla których wartość funkcji jest dodatnia;
c) argumenty, dla których wartość funkcji jest ujemna.

Rozwiązanie
Zauważamy, że:
a) wykres przecina oś w punktach oraz . Zatem oraz są miejscami zerowymi funkcji ;
b) funkcja przyjmuje wartości dodatnie w przedziale oraz w przedziale ;
c) funkcja przyjmuje wartości ujemne w przedziale .
Zdefiniujemy teraz, co to znaczy, że funkcja rośnie, maleje lub jest stała w przedziale . Intuicyjnie pojęcia te przedstawiają rysunki poniżej.
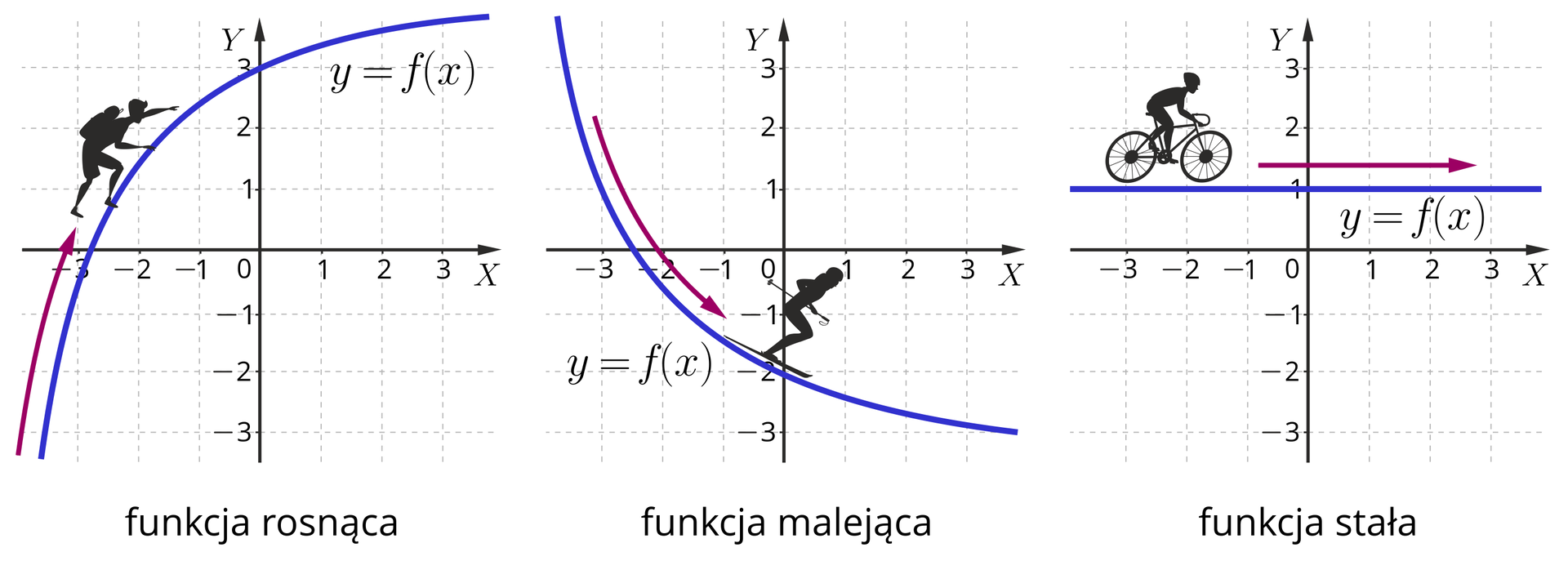
Funkcja rośnie w przedziale , jeśli dla każdych argumentów oraz z tego przedziału prawdą jest, że:
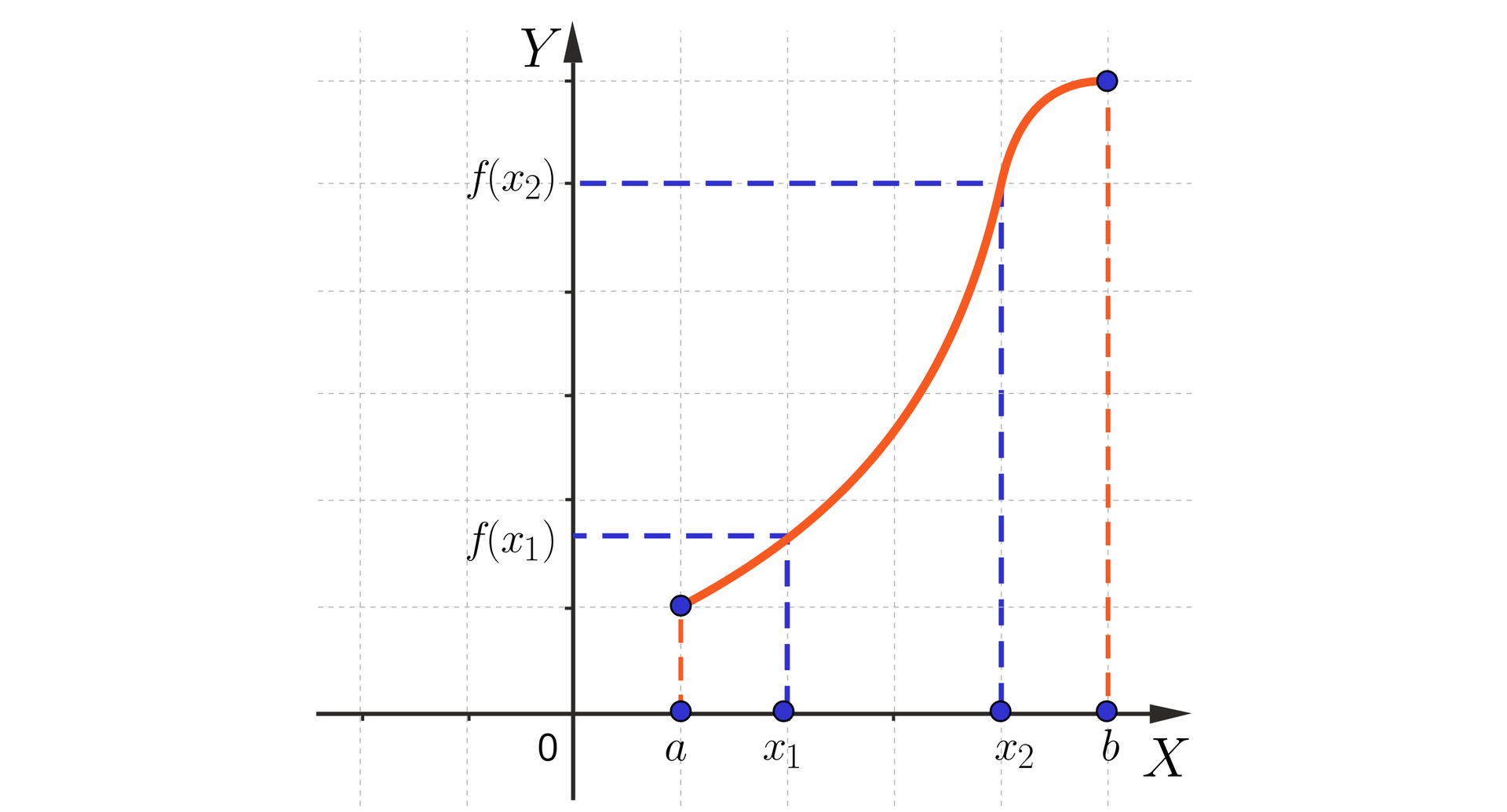
Wykres funkcji jest dany na rysunku poniżej. Dla jakich argumentów funkcja jest rosnąca?

Rozwiązanie
Z rysunku odczytujemy, że funkcja rośnie w przedziale .
Funkcja maleje w przedziale , jeśli dla każdych argumentów oraz z tego przedziału prawdą jest, że:

Dla jakich argumentów funkcja jest malejąca?
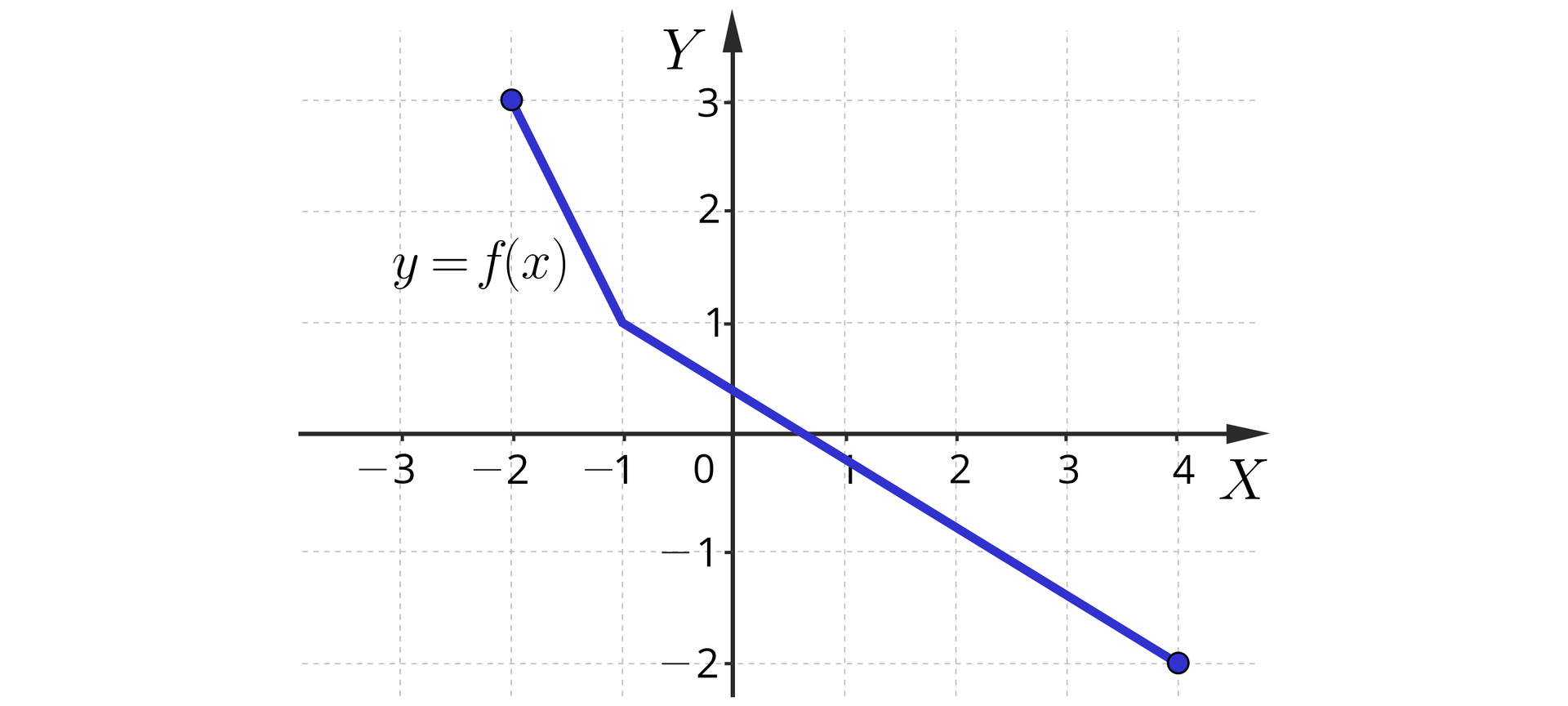
Rozwiązanie
Z rysunku można odczytać, że funkcja jest malejąca w przedziale .
Jeśli funkcja w danym przedziale ani nie rośnie, ani nie maleje, tylko stale ma tę samą wartość, to mówimy, że jest ona stała w tym przedziale.
Funkcja jest stała w przedziale , jeśli dla każdych argumentów oraz z tego przedziału zachodzi równość:
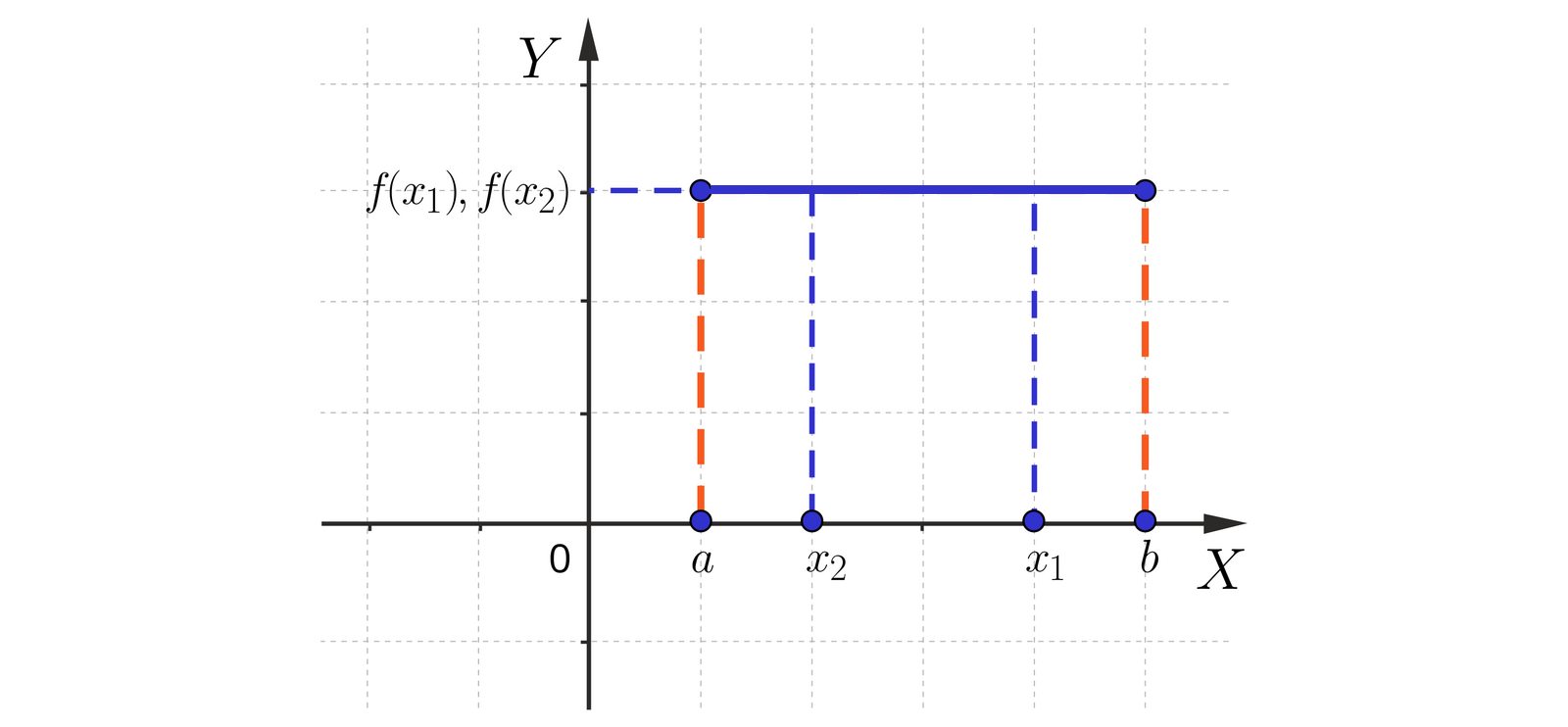
Dla jakich argumentów funkcja przedstawiona na rysunku poniżej jest stała?
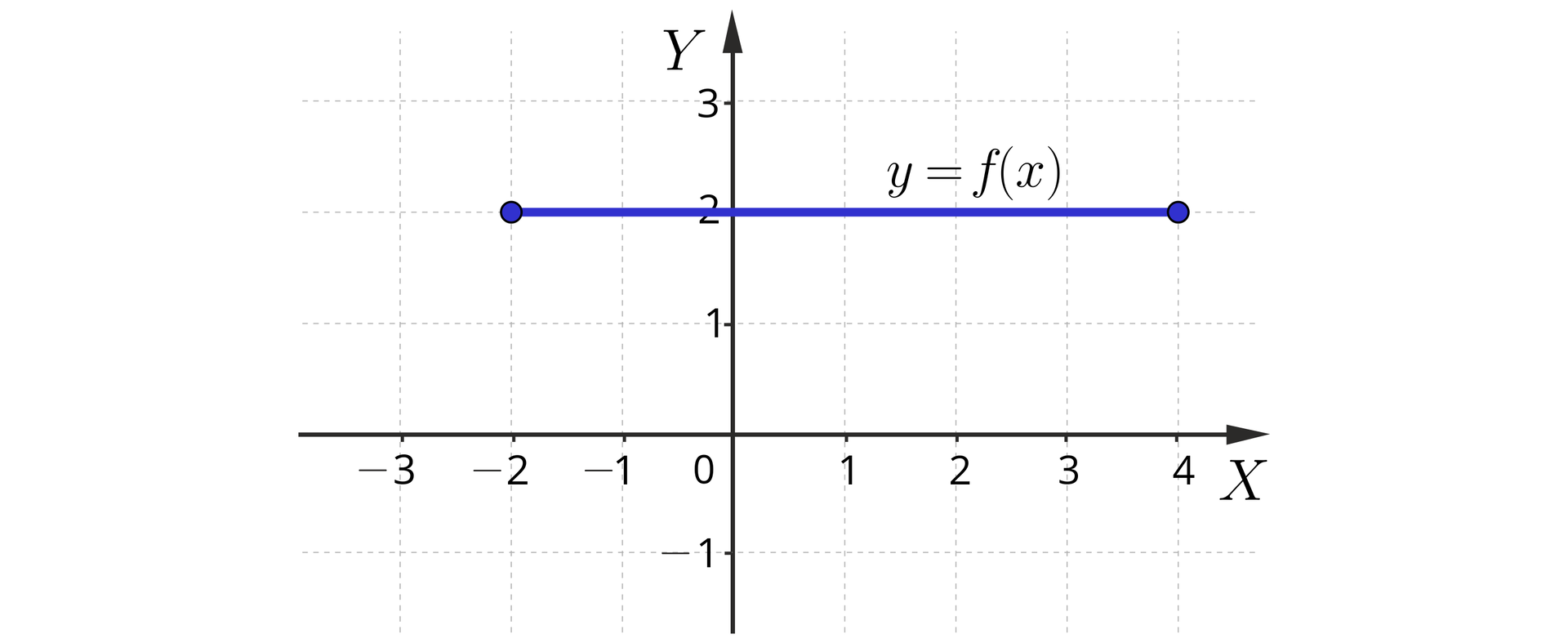
Rozwiązanie
Z rysunku powyżej można odczytać, że funkcja jest stała w przedziale .
Wszelkie funkcje, które w danym przedziale rosną, maleją, albo są stałe, nazywamy funkcjami monotonicznymi w tym przedziale. Oczywiście w całej swojej dziedzinie funkcja może w pewnych przedziałach maleć, a w innych rosnąć, a w jeszcze innych być stała.
Jakie własności ma funkcja przedstawiona na rysunku poniżej?
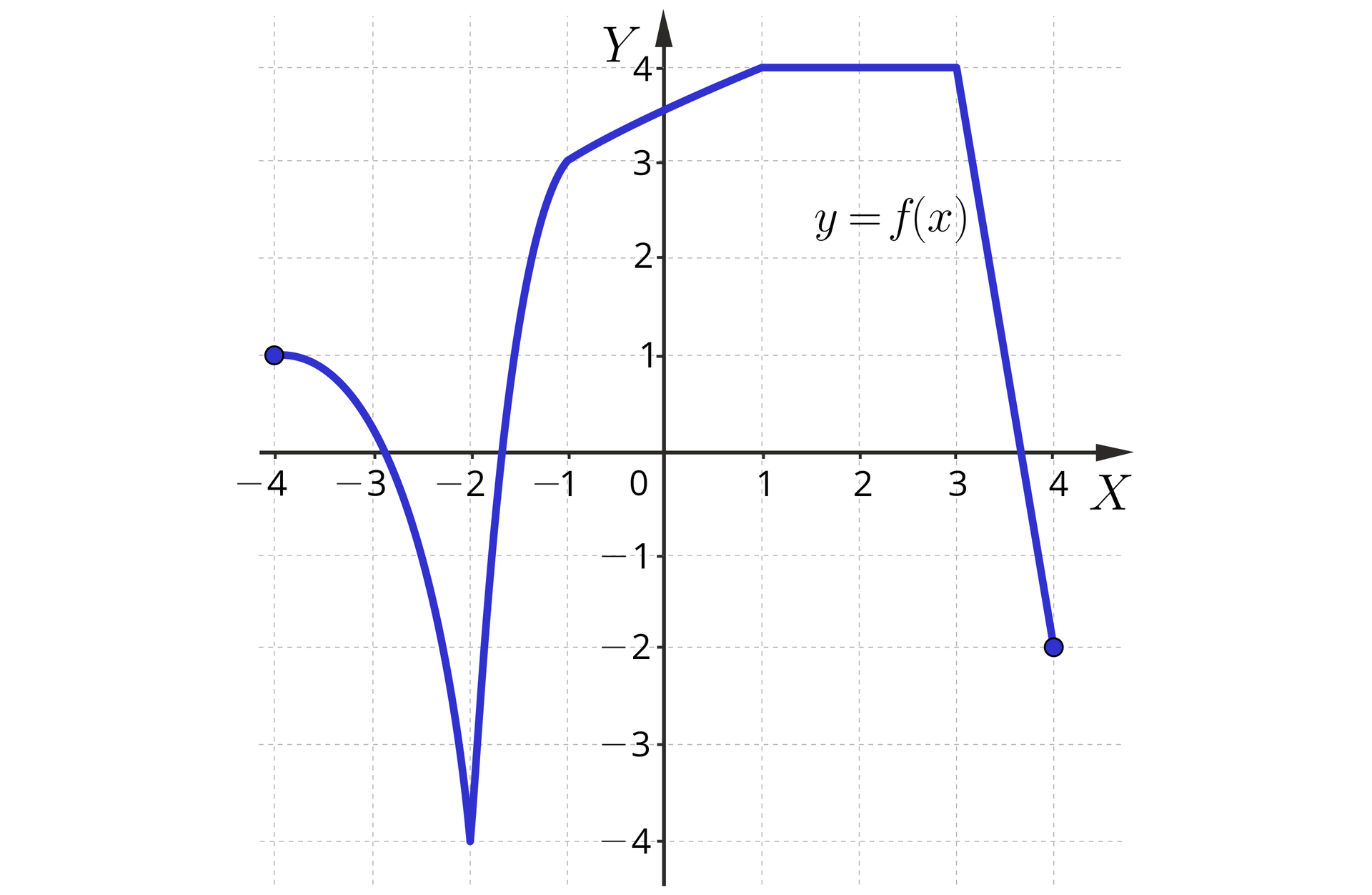
Rozwiązanie
Funkcja :
maleje w przedziale ;
rośnie w przedziale ;
jest stała w przedziale ;
maleje w przedziale .
Widzimy, że w całej swej dziedzinie, czyli w przedziale , funkcja nie jest monotoniczna.
Funkcja, która rośnie (maleje) w jakimś przedziale, rośnie (maleje) też w każdym przedziale w nim zawartym. Dlatego wygodnie jest zdefiniować największy przedział, w jakim dana funkcja rośnie (maleje).
Mówimy, że przedział jest maksymalnym przedziałem, w którym funkcja rośnie, jeśli funkcja rośnie w przedziale , lecz nie rośnie w żadnym większym przedziale zawierającym .
Podobnie definiujemy maksymalne przedziały, w których funkcja maleje.
Jakie własności ma funkcja przedstawiona na poniższym rysunku?
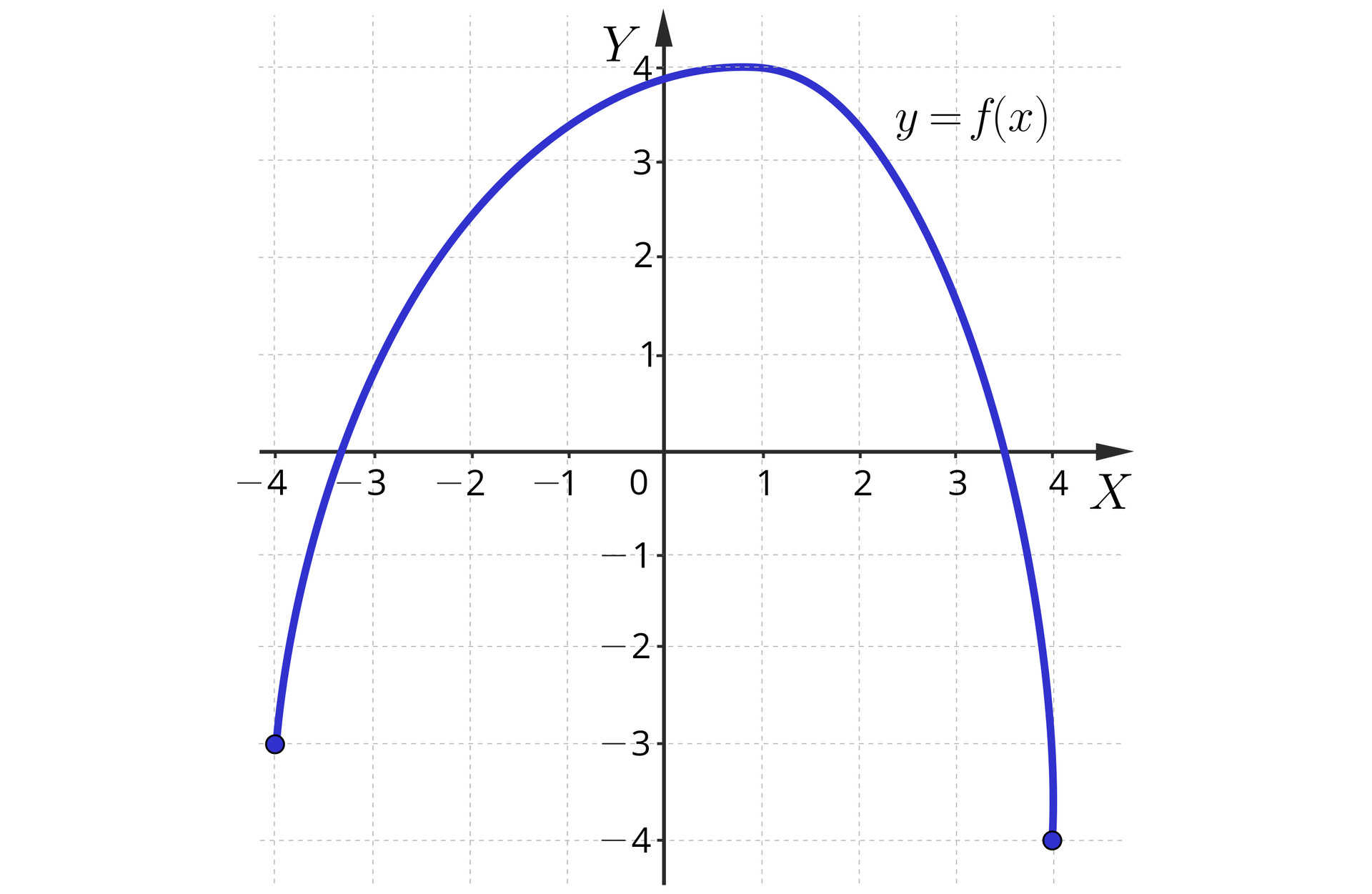
Rozwiązanie
Funkcja :
rośnie w przedziale , ale maksymalnym przedziałem, w którym ta funkcja rośnie jest przedział ;
maleje w przedziale , ale maksymalnym przedziałem, w którym ta funkcja maleje, jest przedział .
Słownik
zmienna niezależna funkcji, będąca elementem jej dziedziny
zbiór wszystkich argumentów funkcji
przyporządkowanie elementom jednego zbioru elementów drugiego zbioru w taki sposób, że każdemu elementowi odpowiada dokładnie jeden element
argument, dla którego funkcja przyjmuje wartość równą zero; miejsce przecięcia wykresu funkcji z osią
zbiór wszystkich liczb, które są wartościami dla argumentów funkcji