Każdy podzbiór skończonego zbioru zdarzeń elementarnych nazywamy zdarzeniem losowym (zdarzeniem).

Doświadczenie polega na jednokrotnym rzucie sześcienną kostką do gry.

RpTIyhHSMphGf

Ilustracja przedstawia sześcienną kostkę do gry, a pod nią narysowano każdą jej ścianę z oczkami osobno.

Każde zdarzenie elementarne w tym doświadczeniu można opisać następująco: wypadło $n$ oczek, gdzie $n\in \left\{1,2,3,4,5,6\right\}$.

Zatem

$\mathrm{\Omega }=\left\{1,2,3,4,5,6\right\}$ i $\left|\mathrm{\Omega }\right|=6$

Rzucamy dwiema sześciennymi kostkami do gry – żółtą i niebieską. Obliczymy, ile jest wszystkich zdarzeń elementarnych w tym doświadczeniu.

Za zdarzenie elementarne przyjmujemy każdą uporządkowaną parę, której elementami są odpowiednio wyniki na żółtej i na niebieskiej kostce.

• sposób $\text{I}$ :

Wykonujemy tabelkę, ilustrującą rzut dwiema kostkami.

RVZ7gPMREaMHU

Ilustracja przedstawia tabelę, w które znajdują się pary wyrzuconych kostek do gry. Pary są następujące: 1 i 1, 1 i 2, 1 i 3, 1 i 4, 1 i 5, 1 i 6, 2 i 1, 2 i 2, 2 i 3, 2 i 4, 2 i 5, 2 i 6, 3 i 1, 3 i 2, 3 i 3, 3 i 4, 3 i 5, 3 i 6, 4 i 1, 4 i 2, 4 i 3, 4 i 4, 4 i 5, 4 i 6, 5 i 1, 5 i 2, 5 i 3, 5 i 4, 5 i 5, 5 i 6, 6 i 1, 6 i 2, 6 i 3, 6 i 4, 6 i 5, 6 i 6

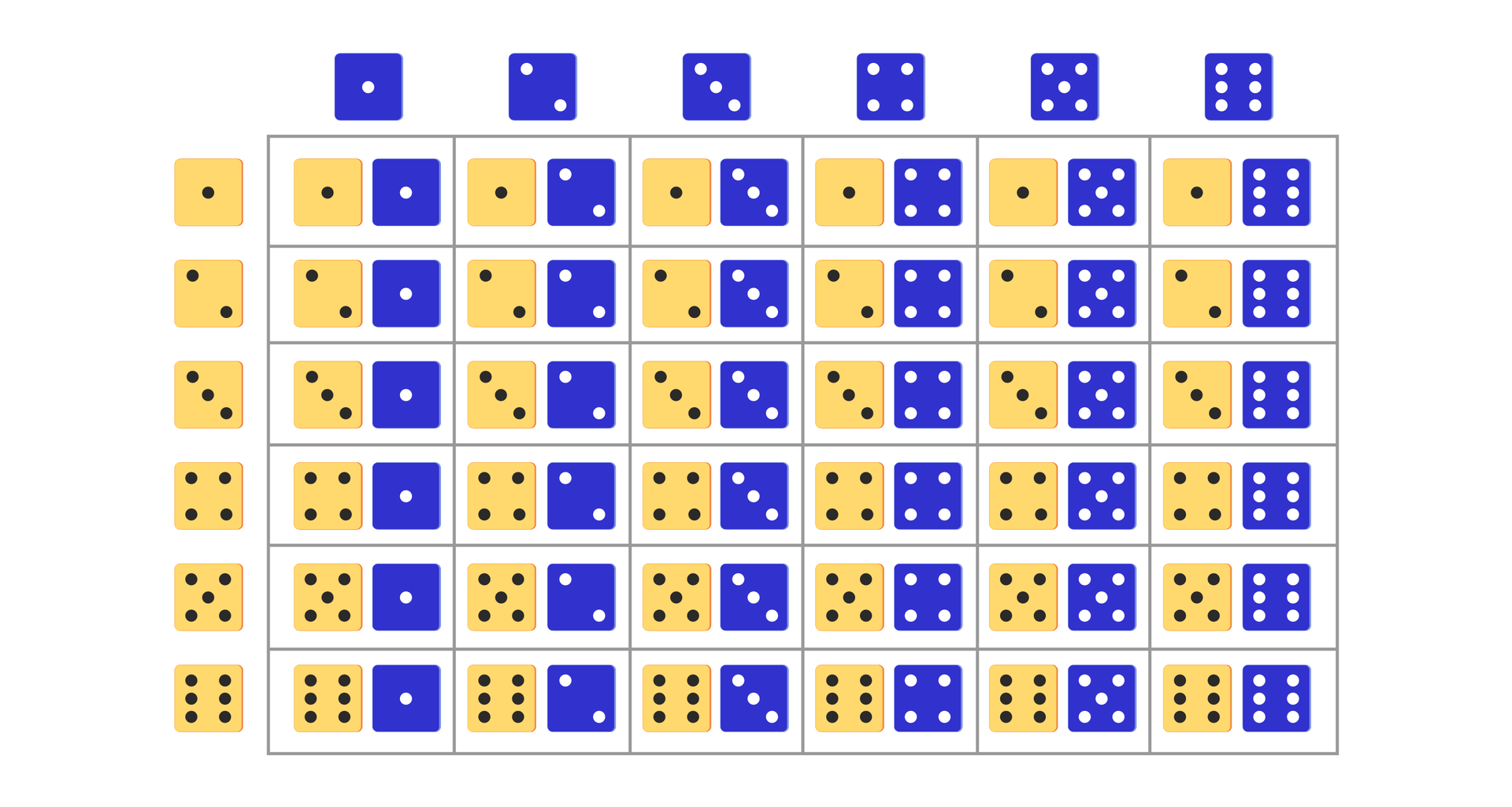
Na podstawie tabelki ustalamy, że jest $36$ zdarzeń elementarnych.

• sposób $\text{II}$:

Zauważmy, że na pierwszej kostce może wypaść $1$, $2$, $3$, $4$, $5$ lub $6$ oczek (jest zatem $6$ różnych możliwości), podobnie na drugiej kostce.

Wszystkich zdarzeń elementarnych jest więc

$\left|\mathrm{\Omega }\right|=6·6=36$

Rzucamy dwukrotnie sześcienną kostką do gry.

Znajdziemy odpowiednie liczby zdarzeń sprzyjających zdarzeniom:

$A$ – suma liczb wyrzuconych oczek jest liczbą pierwszą,

$B$ – iloczyn liczb wyrzuconych oczek jest co najmniej równy $15$,

$C$ – liczba oczek, która wypadła za pierwszym razem jest większa od liczby oczek, która wypadła za drugim razem.

Sporządzamy pomocniczą tabelkę. W pola tabelki wpisujemy możliwe do otrzymania sumy liczb oczek w dwukrotnym rzucie sześcienną kostką do gry i zaznaczamy zdarzenia sprzyjające zdarzeniu $A$ – suma liczb wyrzuconych oczek jest liczbą pierwszą.

RUKdYApq4Un28

Ilustracja przedstawia tabelę, w komórkach której zapisano sumę oczek wyrzuconych na dwóch kostkach. Numer kolumny i wiersza pokrywa się z liczbą wyrzuconych oczek, czyli na przykład pierwsza kolumna to wyrzucona na jednej z kostek jedynka. Niektóre pola są wyróżnione kolorem. Wiersz pierwszy: 2 wyróżnione, 3 wyróżnione, 4, 5 wyróżnione, 6, 7 wyróżnione, wiersz drugi: 3 wyróżnione, 4, 5 wyróżnione, 6, 7 wyróżnione, 8, wiersz trzeci: 4, 5 wyróżnione, 6, 7 wyróżnione, 8, 9, wiersz czwarty: 5 wyróżnione, 6, 7 wyróżnione, 8, 9, 10, wiersz piąty: 6, 7 wyróżnione, 8, 9, 10, 11 wyróżnione, wiersz szósty: 7 wyróżnione, 8, 9, 10, 11 wyróżnione, 12

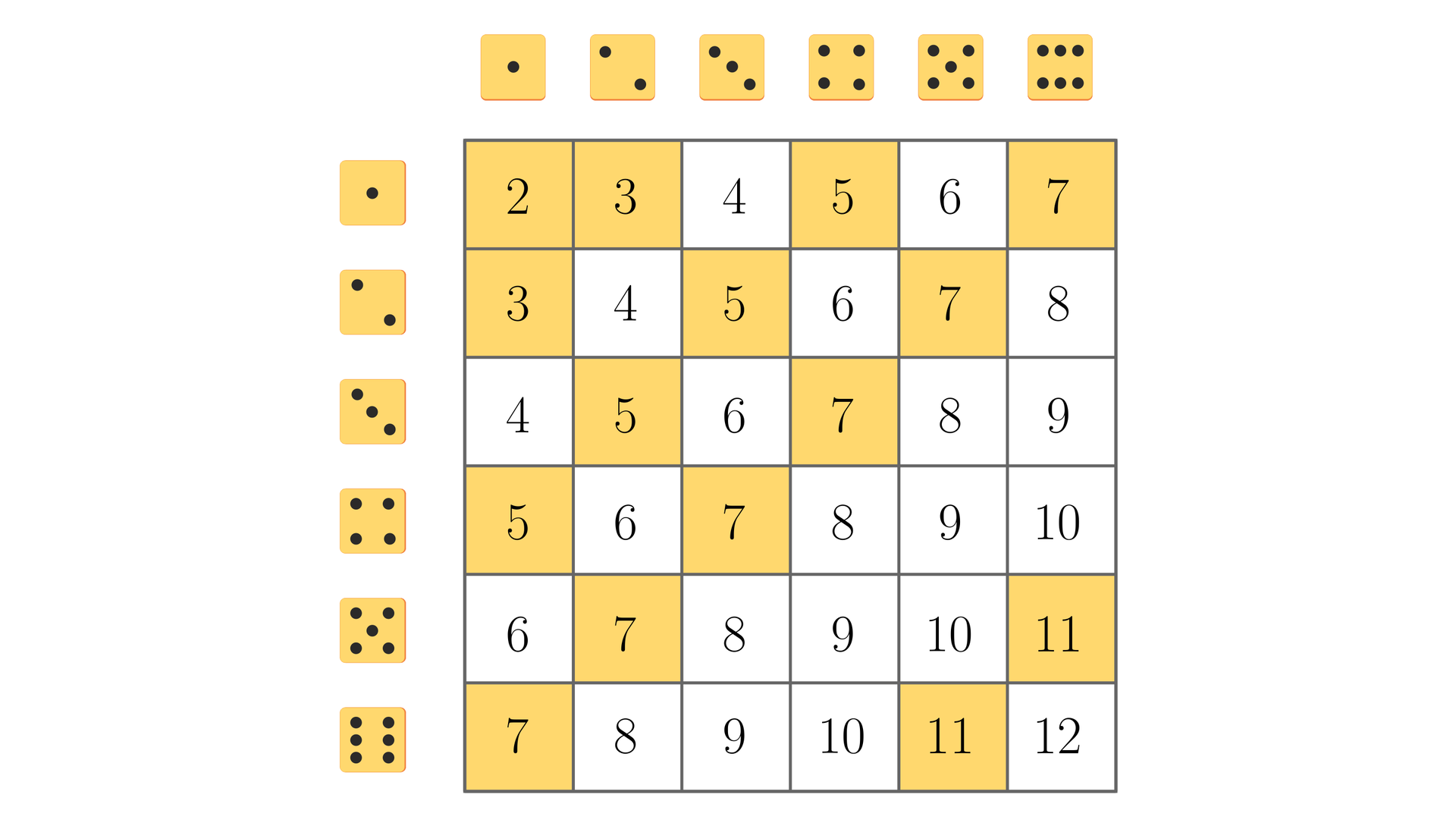
Odczytujemy z tabelki: $\left|A\right|=15$.

Sporządzamy kolejną tabelkę, w której pola tym razem wpisujemy możliwe do uzyskania iloczyny liczb oczek w dwukrotnym rzucie sześcienną kostką do gry. Zaznaczamy zdarzenia sprzyjające zdarzeniu $B$ – iloczyn liczb wyrzuconych oczek jest co najmniej równy $15$.

RPT0MaYbplMda

Ilustracja przedstawia tabelę, w komórkach której zapisano iloczyn oczek wyrzuconych na dwóch kostkach. Numer kolumny i wiersza pokrywa się z liczbą wyrzuconych oczek, czyli na przykład pierwsza kolumna to wyrzucona na jednej z kostek jedynka. Niektóre pola są wyróżnione kolorem. Wiersz pierwszy: 1, 2, 3, 4, 5, 6, wiersz drugi: 2, 4, 6, 8, 10, 12, wiersz trzeci: 3, 6, 9, 12, 15 wyróżnione, 18 wyróżnione, wiersz czwarty:4, 8, 12, 16 wyróżnione, 20 wyróżnione, 24 wyróżnione, wiersz piąty: 5, 10, 15 wyróżnione, 8, 9, 10, 11 wyróżnione, 20 wyróżnione, 25 wyróżnione, 30 wyróżnione, wiersz szósty: 6, 12, 18 wyróżnione, 24 wyróżnione, 30 wyróżnione, 36 wyróżnione

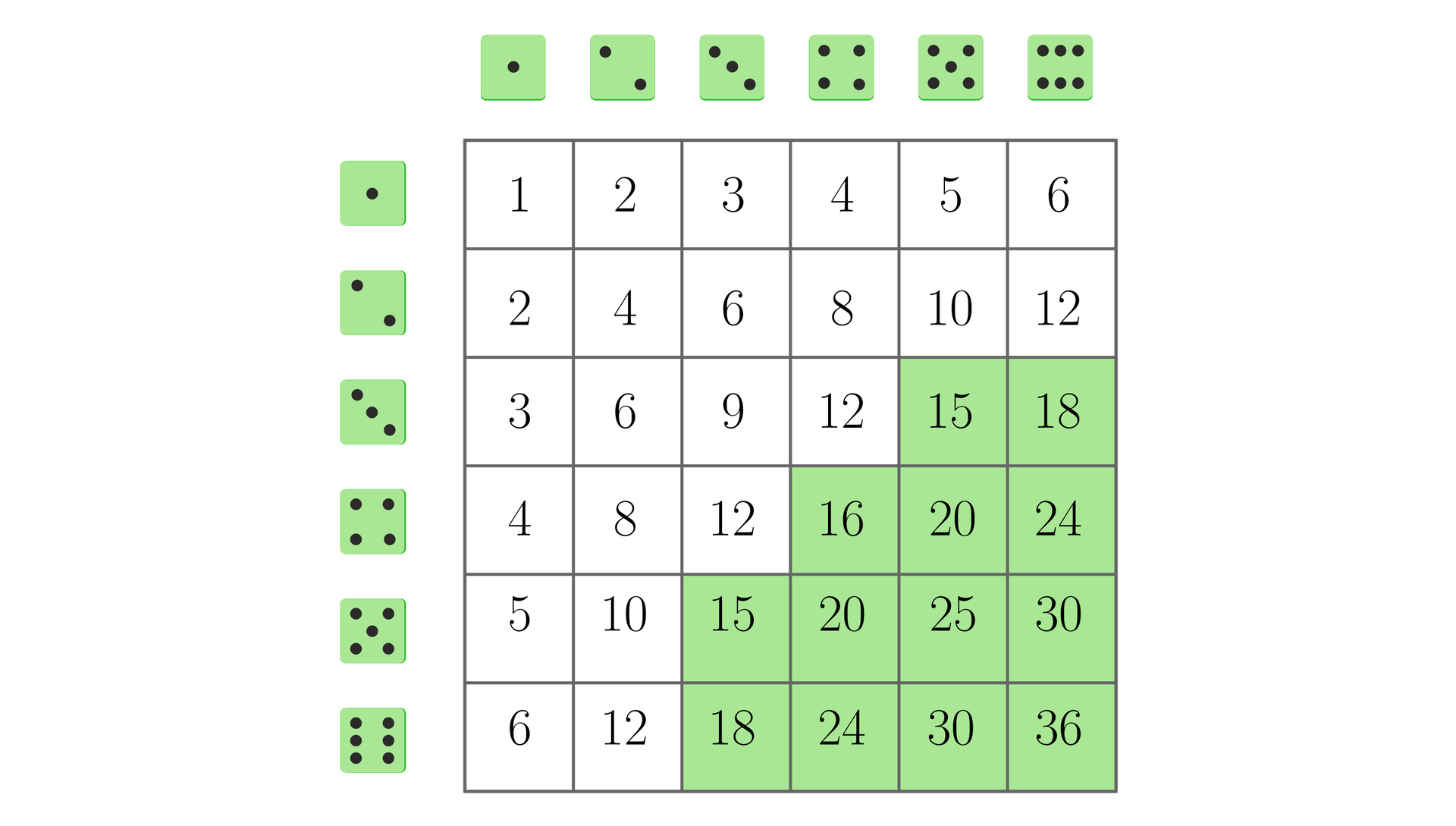
Odczytujemy z tabelki: $\left|B\right|=13$.

Sporządzamy ponownie tabelkę, w pola której wpisujemy wszystkie możliwe układy liczb, jakie mogą zajść w dwukrotnym rzucie sześcienną kostką do gry. Zaznaczamy zdarzenia sprzyjające zdarzeniu $C$ – liczba oczek, która wypadła za pierwszym razem jest większa od liczby oczek, która wypadła za drugim razem.

RRz2aW8gLcscl

Ilustracja przedstawia tabelę, w które znajdują się pary wyrzuconych kostek do gry. Niektóre komórki tabeli są wyróżnione. Pary są następujące: 1 i 1, 2 i 1 wyróżnione, 3 i 1 wyróżnione, 4 i 1 wyróżnione, 5 i 1 wyróżnione, 6 i 1 wyróżnione, wiersz drugi: 1 i 2, 2 i 2, 3 i 2 wyróżnione, 4 i 2 wyróżnione, 5 i 2 wyróżnione, 6 i 2 wyróżnione, 1 i 3, 2 i 3, 3 i 3, 4 i 3 wyróżnione, 5 i 3 wyróżnione, 6 i 3 wyróżnione, wiersz czwarty: 1 i 4, 2 i 4, 3 i 4, 4 i 4, 5 i 4 wyróżnione, 6 i 4 wyróżnione, 1 i 5, 2 i 5, 3 i 5, 4 i 5, 5 i 5, 6 i 5 wyróżnione, wiersz szósty: 1 i 6, 2 i 6, 3 i 6, 4 i 6, 5 i 6, 6 i 6

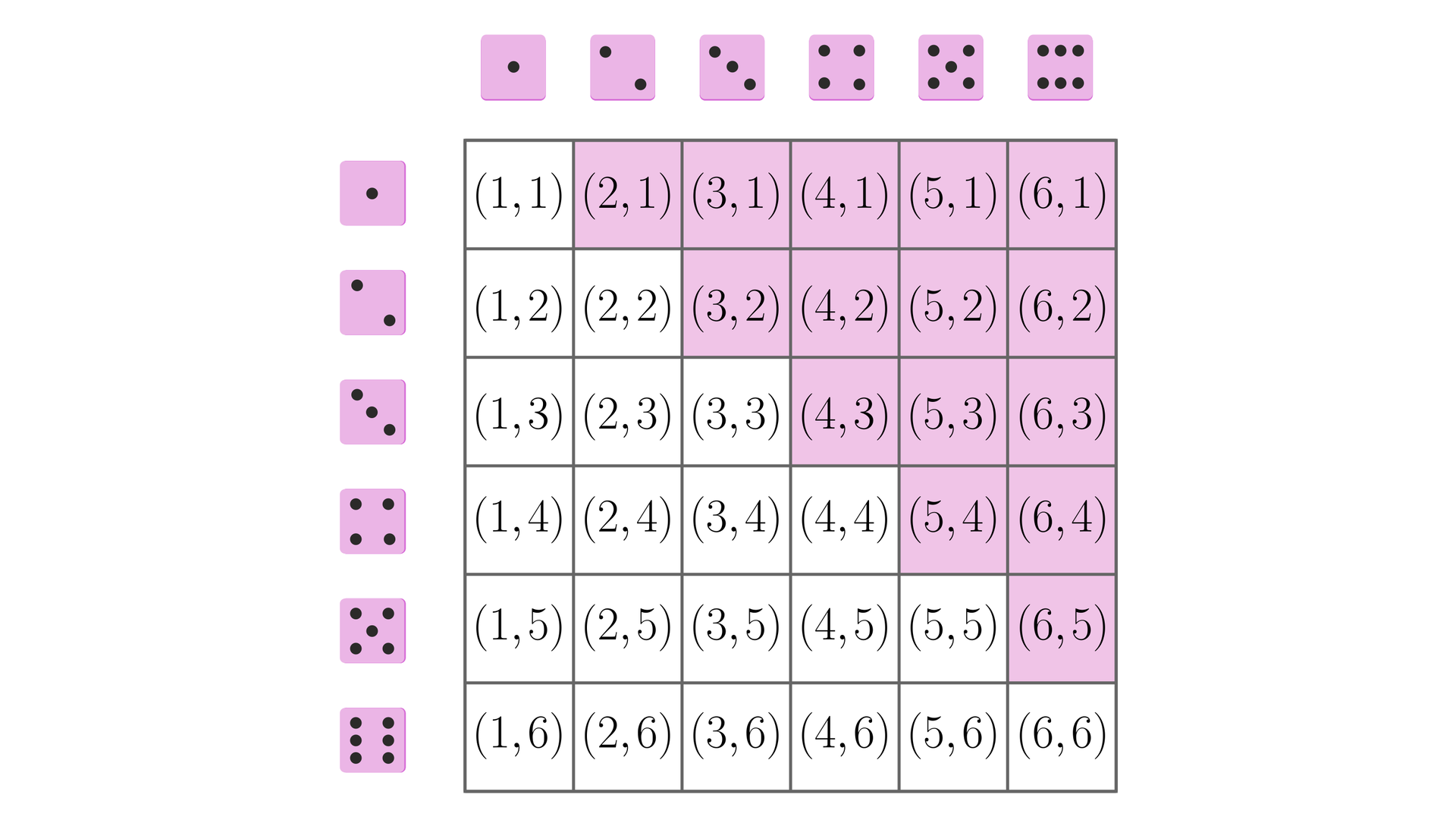
Z tabelki odczytujemy: $\left|C\right|=15$.

Doświadczenie losowe polega na trzykrotnym rzucie sześcienną kostką do gry.

Wypiszemy zdarzenia sprzyjające zdarzeniu: $A$ – w każdym rzucie wypadła liczba oczek, będąca drugą potęgą liczby naturalnej.

Skorzystamy z interpretacji graficznej doświadczenia, zaznaczając na „drzewku” tylko odpowiednie krawędzie. Zauważmy przy tym, że potęgami liczb naturalnych są w tym przypadku tylko liczby oczek równe $1$ i $4$.

R5QmThuPj6Qsn

Ilustracja

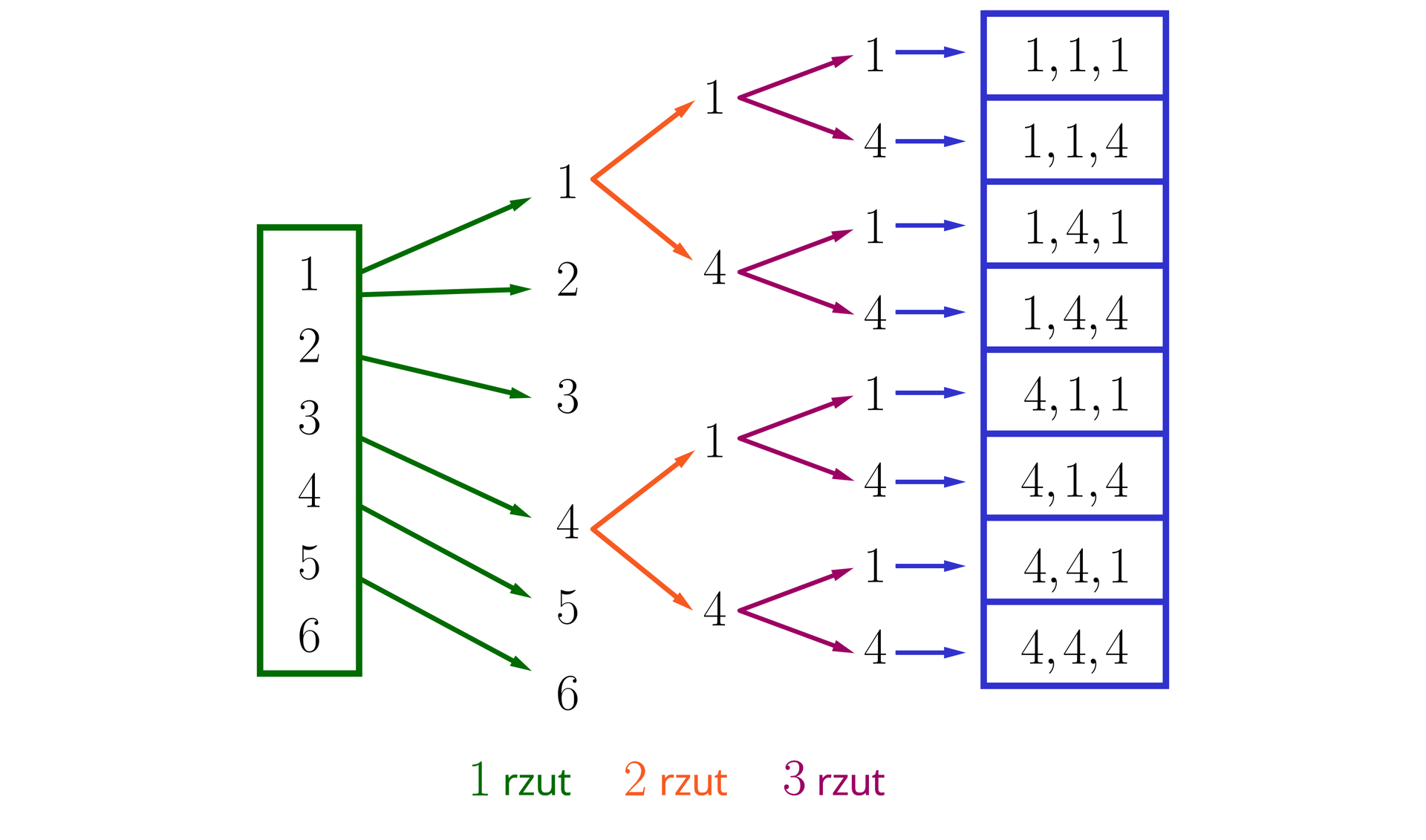
Schemat rzutów kostką:

• Możliwości w rzucie pierwszym: 1, 2, 3, 4, 5, 6

• Możliwości w rzucie drugim: 1, 4;
  mamy więc następujące możliwości po rzucie drugim:

  1. 1 1,

  2. 1 4,

  3. 4 1,

  4. 4 4;

• Możliwości w rzucie trzecim: 1, 4; mamy więc następujące możliwości:

  1. 1 1 1,

  2. 1 1 4,

  3. 1 4 1,

  4. 1 4 4,

  5. 4 1 1,

  6. 4 1 4,

  7. 4 4 1,

  8. 4 4 4

Odczytujemy z „drzewka”:

$A=\left\{\left(1,1,1\right),\left(1,1,4\right),\left(1,4,1\right),\left(1,4,4\right),\left(4,1,1\right),\left(4,1,4\right),\left(4,4,1\right),\left(4,4,4\right)\right\}$

Jeżeli piszemy o rzucie kilkoma sześciennymi kostkami do gry, to zakładamy, że kostki te są rozróżnialne.

Zatem doświadczenia: $n$ krotny rzut kostką i rzut $n$ kostkami, interpretujemy i opisujemy tak samo. Czyli identyczne są zbiory zdarzeń elementarnych takich doświadczeń.

Zauważmy, że w jednoczesnym rzucie $n$ sześciennymi kostkami do gry (lub w $n$ rzutach kostką) liczba zdarzeń elementarnych jest równa $6^n$.

Rzucamy pięć razy sześcienną kostką do gry. Obliczymy, ile jest

1. zdarzeń elementarnych w tym doświadczeniu losowym,

2. zdarzeń sprzyjających zdarzeniom:
   $A$ – pięć razy otrzymamy liczbę oczek równą $6$,
   $B$ – tylko w pierwszym i trzecim rzucie otrzymamy liczbę oczek równą $6$,
   $C$ – czterokrotnie wyrzucimy liczbę oczek równą $6$.

Rozwiązanie:

1. Aby wyznaczyć liczbę zdarzeń elementarnych, korzystamy ze wzoru na wariację z powtórzeniami.
   $\left|\mathrm{\Omega }\right|=6^5=7776$

2. Jest tylko jedna możliwość, żeby za każdym razem otrzymać liczbę oczek równą $6$.
   $\left|A\right|=1$
   Zdarzeniu $B$ sprzyja tyle zdarzeń elementarnych, ile można utworzyć trzyelementowych wariacji z powtórzeniami zbioru pięcioelementowego (za drugim, czwartym i piątym razem może wypaść liczba oczek różna od $6$).
   $\left|B\right|=5^3=125$
   Zbiór zdarzeń sprzyjających czterokrotnemu wyrzuceniu liczby oczek równej sześć, możemy opisać następująco:
   $C=\left\{\left(n,6,6,6,6\right),\left(6,n,6,6,6\right),\dots ,\left(6,6,6,6,n\right)\right\}$, gdzie $n\in \left\{1,2,3,4,5\right\}$.
   Zatem
   $\left|C\right|=5·5=25$

Rzucamy dwukrotnie kostką do gry w kształcie czworościanu foremnego, na ściankach którego zapisane są liczby $1$, $2$, $3$, $4$.

R3aQuw2Z8iX3t

Ilustracja przedstawia czworościan. Ściany tej bryły są trójkątami opisanymi numerami: 1, 2, 3, 4

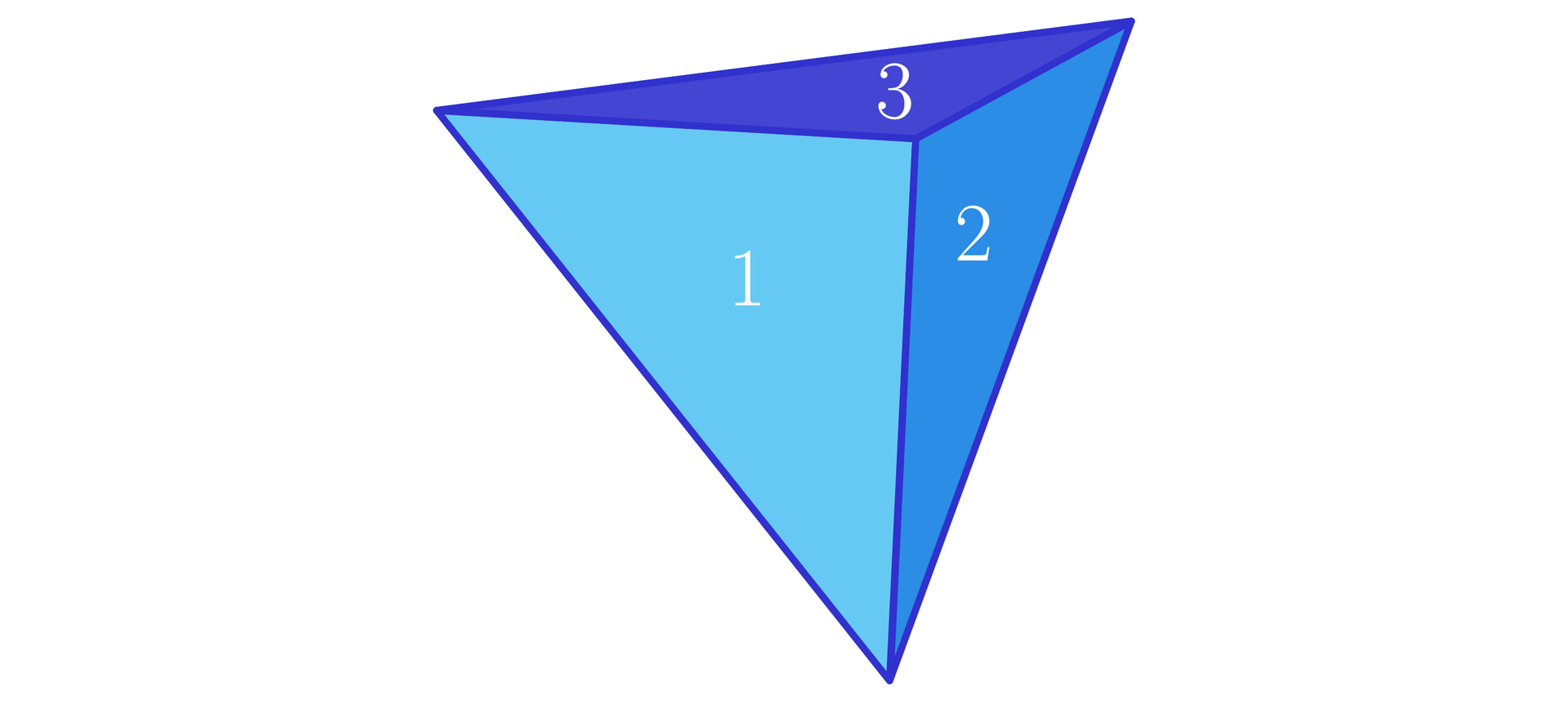
Wynikiem jednego rzutu jest liczba zapisana na ściance, na której upadła kostka.

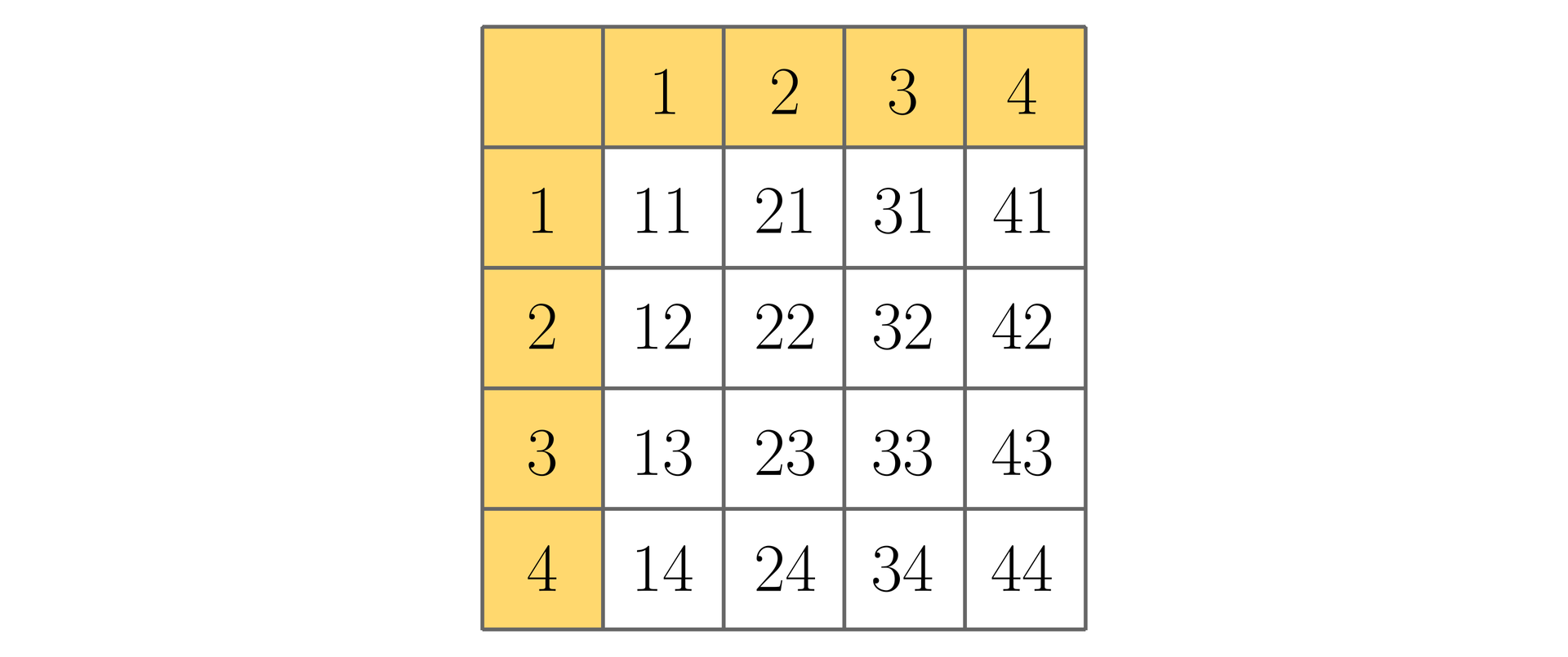
Zapisujemy kolejno liczby, które wypadają tak, że powstają liczby dwucyfrowe. Cyfra dziesiątek, to cyfra otrzymana w pierwszym rzucie, cyfra jedności – w drugim rzucie.

Oznaczmy:

$A$– zdarzenie polegające na otrzymaniu liczby nieparzystej,

$B$ – zdarzenie polegające na otrzymaniu liczby większej od $35$,

$C$ – zdarzenie polegające na utworzeniu liczby podzielnej przez $7$.

Określamy najpierw zbiór zdarzeń elementarnych w tabeli.

R1bNyixyuyhMN

Ilustracja przedstawia tabelkę, wiersz nagłówkowy składa się z czterech komórek, w których wpisane są kolejno cyfry od 1 do 4, kolumna nagłówkowa składa się z czterech komórek, w które wpisano kolejno cyfry od 1 do 4; wiersz pierwszy składa się z czterech komórek, w które wpisano kolejno liczby: 11, 21, 31, 41, wiersz drugi: 12, 22, 32, 42, wiersz trzeci: 13, 23, 33, 43, wiersz czwarty: 14, 24, 34, 44

$A=\left\{11,13,21,23,31,33,41,43\right\}$

$B=\left\{41,42,43,44\right\}$

$C=\left\{14,21,42\right\}$

$A\cap B$

$A\cup B$

$B\cap C$

$A\cap B=\left\{41,43\right\}$

$A\cup B=\left\{11,13,21,23,31,33,41,42,43,44\right\}$

$B\cap C=\left\{42\right\}$

każdy podzbiór skończonego zbioru zdarzeń elementarnych nazywamy zdarzeniem losowym (zdarzeniem)