Przeczytaj

Wzór funkcji kwadratowej $f (x) = a x^{2} + b x + c$ , $x \in ℝ$ , gdzie $a$ , $b$ , $c$ są liczbami rzeczywistymi, przy czym $a \neq 0$ , możemy zapisać w postaci kanonicznej: $f (x) = a {(x - \frac{b}{2 a})}^{2} - \frac{Δ}{4 a}$ , gdzie $x_{w} = - \frac{b}{2 a}$ , $y_{w} = - \frac{Δ}{4 a}$ są współrzędnymi wierzchołka paraboli będącej wykresem funkcji $f$ .

Analizując postać kanonicznąpostać kanoniczna funkcji kwadratowejpostać kanoniczną funkcji kwadratowej otrzymujemy, że

dla $a > 0$ wartość wyrażenia $a {(x + \frac{b}{2 a})}^{2}$ jest nieujemna. Jeśli $x = - \frac{b}{2 a}$ , to wartość tego wyrażenia jest najmniejsza - równa $0$ . Stąd najmniejsza wartość funkcji kwadratowej $y_{\min} = - \frac{Δ}{4 a}$ ;

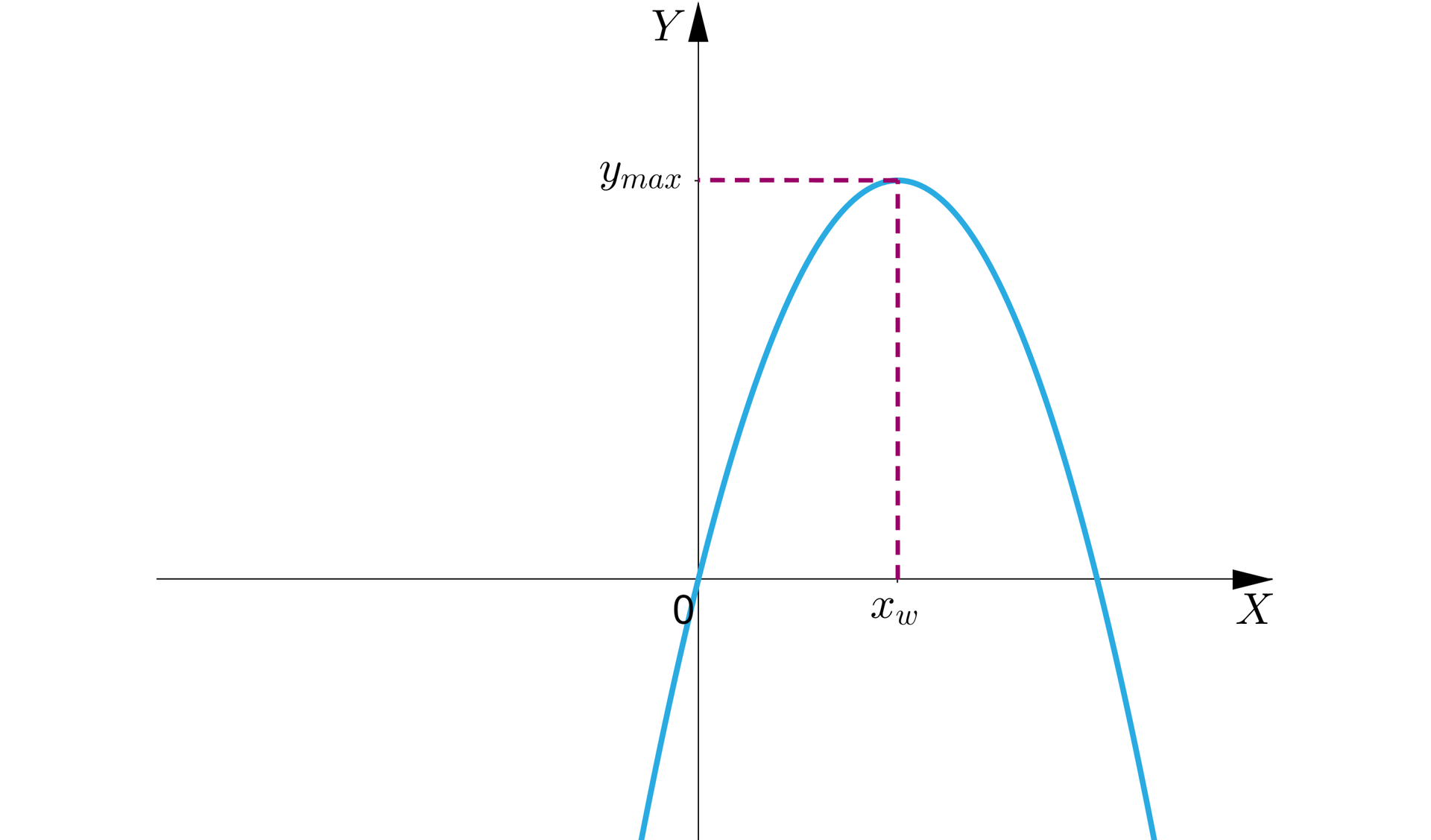
dla $a < 0$ wartość wyrażenia $a {(x + \frac{b}{2 a})}^{2}$ jest niedodatnia. Jeśli $x = - \frac{b}{2 a}$ , to wartość tego wyrażenia jest największa - równa $0$ . Stąd największa wartość funkcji kwadratowej $y_{\max} = - \frac{Δ}{4 a}$ .

Istnienie najmniejszej lub największej wartości funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej zależy od współczynnika $a$ .

Jeśli $a > 0$ , to funkcja $y = a x^{2} + b x + c$ przyjmuje wartość najmniejszą $y_{\min} = - \frac{Δ}{4 a}$ dla $x = - \frac{b}{2 a}$ .

R1YwNVBa6t5Tu

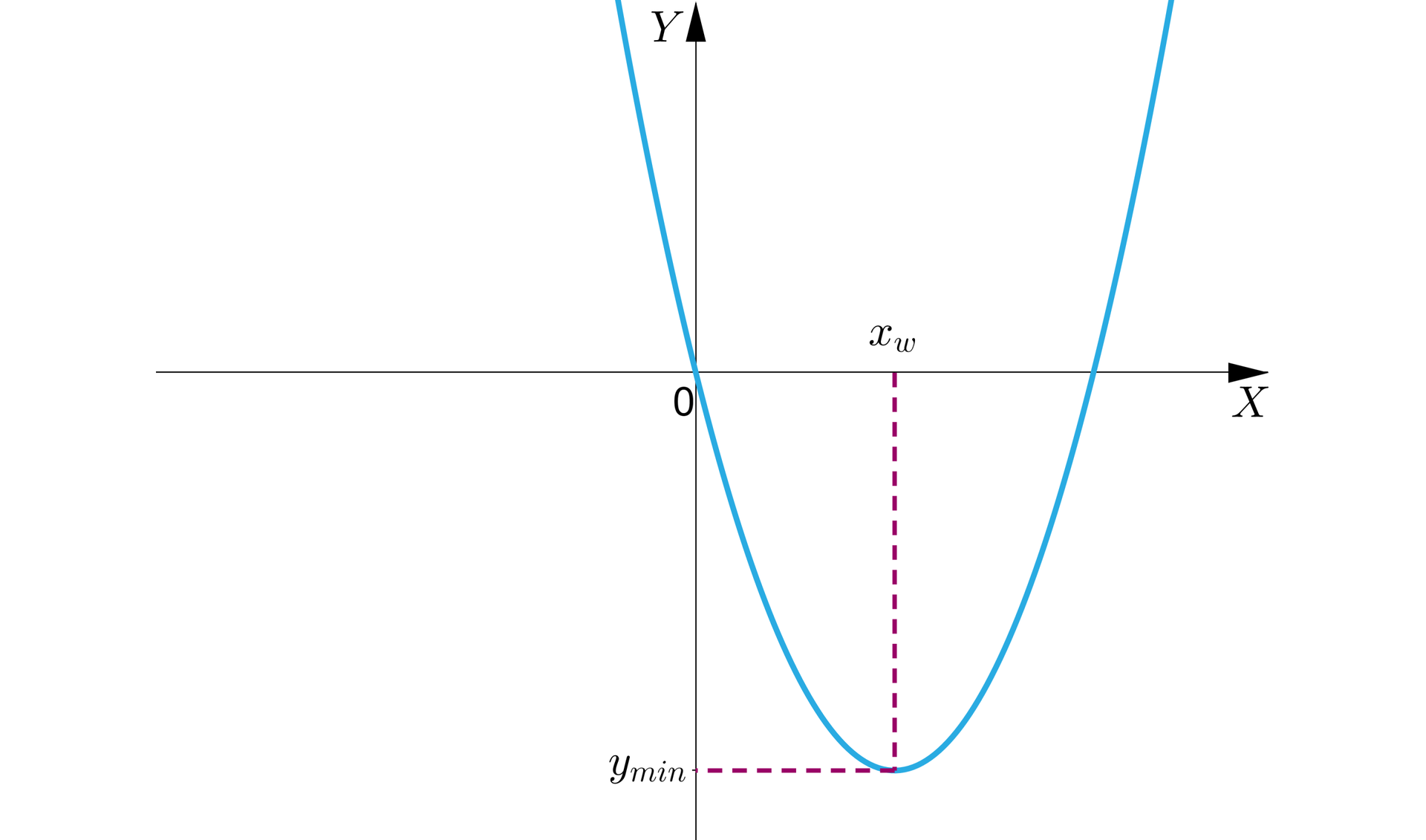
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X, oraz z pionową osią Y. Na płaszczyźnie narysowano parabolę, której wierzchołek znajduje się w czwartej ćwiartce układu współrzędnych, a jej ramiona skierowane są w górę. Z wierzchołka poprowadzono linią przerywaną prostą prostopadłą do osi X w punkcie xw, oraz prostą prostopadłą do osi Y w punkcie ymin.

Jeśli $a < 0$ , to funkcja $y = a x^{2} + b x + c$ przyjmuje wartość największą $y_{\max} = - \frac{Δ}{4 a}$ dla $x = - \frac{b}{2 a}$ .

R1w9G5TjWonnd

Przykład 1

Wyznaczymy najmniejszą wartość funkcji kwadatowej $f (x) = 2 x^{2} + 4 x - 1$ , gdy $x \in ℝ$ .

Rozwiązanie

$a > 0$ , więc funkcja $f (x)$ przyjmuje wartość najmniejszą $y_{\min} = - \frac{Δ}{4 a}$ dla $x_{w} = - \frac{b}{2 a}$ .

Sprowadźmy trójmian do postaci kanonicznej:

$2 x^{2} + 4 x - 1 = 2 (x^{2} + 2 x - \frac{1}{2}) = 2 (x^{2} + 2 \cdot x + 1 - 1 - \frac{1}{2}) =$

$= 2 ((x^{2} + 2 \cdot x + 1) - 1 - \frac{1}{2}) = 2 ({(x + 1)}^{2} - \frac{3}{2}) = 2 {(x + 1)}^{2} - 3$ .

Wykorzystaliśmy wzór skróconego mnożenia:

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

$f (x) = 2 {(x + 1)}^{2} - 3$ ,

więc $x_{w} = - 1$ i $y_{m i n} = - 3$ .

Odpowiedź

Funkcja przyjmuje wartość najmniejszą równą $(- 3)$ dla $x = - 1$ .

Przykład 2

Wyznaczymy największą wartość funkcji $f (x) = - x^{2} + x + 20$ .

Rozwiązanie

$a < 0$ , więc funkcja $f (x)$ przyjmuje wartość największą $y_{\max} = - \frac{Δ}{4 a}$ dla $x_{w} = - \frac{b}{2 a}$ .

Sprowadźmy trójmian do postaci kanonicznej. Wykorzystamy wzory $x_{w} = - \frac{b}{2 a}$ i $y = - \frac{Δ}{4 a}$ .

$x_{w} = - \frac{1}{2 \cdot (- 1)} = \frac{1}{2}$ i $a < 0$ , to $y_{\max} = - \frac{Δ}{4 a}$ .

$Δ = b^{2} - 4 a c = 1^{2} - 4 (- 1) (20) = 1 + 80 = 81$ , to $y_{m a x} = - \frac{Δ}{4 a} = \frac{- 81}{4 (- 1)} = \frac{81}{4}$ .

Odpowiedź

Funkcja osiąga wartość największą $\frac{81}{4}$ dla $x = \frac{1}{2}$ .

Przykład 3

Wyznaczymy współczynniki $a$ , $b$ , $c$ we wzorze funkcji kwadratowej $y = a x^{2} + b x + c$ , jeśli wiadomo, że dla $x = 1$ funkcja przyjmuje wartość największą równą $2$ , zaś dla $x = 2$ przyjmuje wartość $1$ .

Rozwiązanie

Funkcja przyjmuje wartość największą równą $2$ dla argumentu równego $1$ .

Współrzędne wierzchołka paraboli: $x_{w} = 1$ i $y_{max} = 2$ .

Możemy zapisać wzór funkcji w postaci kanonicznej:

$f (x) = a {(x - 1)}^{2} + 2$ ,

ponieważ $f (2) = 1 \to 1 = a {(2 - 1)}^{2} + 2 \to 1 = a + 2 \to a = - 1$ .

Wyznaczymy współczynniki $b$ i $c$ , zapisując wzór funkcji w postaci ogólnej: $f (x) = a x^{2} + b x + c$ .

$f (x) = - {(x - 1)}^{2} + 2 = - (x^{2} - 2 x + 1) + 2 =$

$= - x^{2} + 2 x - 1 + 2 = - x^{2} + 2 x + 1$

Porównując zapisy $f (x) = a x^{2} + b x + c$ oraz $f (x) = - x^{2} + 2 x + 1$ widzimy, że $b = 2$ i $c = 1$ .

Odpowiedź

$a = - 1$ , $b = 2$ , $c = 1$ .

Gdy ograniczamy się do rozpatrywania wartości funkcji kwadratowej w danym przedziale $⟨x_{1}, x_{2}⟩$ , to poszukujemy wartości najmniejszej i największej pośród liczb: $f (x_{w})$ , $f (x_{1})$ , $f (x_{2})$ , gdy $x_{w} \in ⟨x_{1}, x_{2}⟩$ , a gdy $x_{w}$ nie należy do tego przedziału funkcja przyjmuje wartość największą/najmniejszą na krańcach tego przedziału.

Przykład 4

Wyznaczymy najmniejszą oraz największą wartość funkcji $f (x) = 2 x^{2} + 16 x + 29$ w przedziale $⟨- 3, 1⟩$ .

Rozwiązanie

Zapisujemy wzór funkcji $f (x) = 2 x^{2} + 16 x + 29$ w postaci kanonicznej:

$f (x) = 2 x^{2} + 16 x + 29 = 2 (x^{2} + 8 x + 16) - 3 = 2 {(x + 4)}^{2} - 3$ ,

stąd $x_{w} = - 4$ i $y_{w} = - 3$ .

Funkcja w zbiorze liczb rzeczywistych przyjmuje wartość najmniejszą równą $(- 3)$ dla $x = - 4$ , bo $a > 0$ . Nie jest to najmniejsza wartość funkcji w podanym przedziale, bo $x = - 4$ nie należy do przedziału $⟨- 3, 1⟩$ .

Wartości największej lub najmniejszej poszukujemy wśród liczb $f (- 3)$ i $f (1)$ .

$f (- 3) = 2 {(- 3 + 4)}^{2} - 3 = 2 \cdot 1^{2} - 3 = 2 - 3 = - 1$

$f (1) = 2 {(1 + 4)}^{2} - 3 = 2 \cdot 5^{2} - 3 = 2 \cdot 25 - 3 = 50 - 3 = 47$

Odpowiedź

W przedziale $⟨- 3, 1⟩$ funkcja przyjmuje wartość najmniejszą $(- 1)$ dla $x = - 3$ , a wartość największą $47$ dla $x = 1$ .

Przykład 5

Sprawdzimy, dla jakich wartości zmiennej $x \in ⟨0, 2⟩$ funkcja $f (x) = \frac{1}{x^{2} - x + 1}$ przyjmuje wartość największą, a dla jakiej najmniejszą.

Rozwiązanie

Ponieważ $Δ = b^{2} - 4 a c = 1^{2} - 4 = - 3 < 0$ , to wyrażenie w mianowniku nie przyjmuje wartości równej zero, czyli dla każdego $x \in ℝ : x^{2} - x + 1 \neq 0$ .

Oznaczamy wyrażenie w mianowniku jako $g (x) = x^{2} - x + 1$ i zapiszmy w postaci kanonicznej:

$g (x) = x^{2} - x + 1 = x^{2} - x + \frac{1}{4} - \frac{1}{4} + 1 = {(x - \frac{1}{2})}^{2} + \frac{3}{4}$ .

$x_{w} = \frac{1}{2}$ i $y_{w} = \frac{3}{4}$ , więc dla $x = \frac{1}{2}$ funkcja $g (x)$ przyjmuje wartość najmniejszą
( $a = 1 > 0$ ) równą $\frac{3}{4}$ , więc iloraz $\frac{1}{g (x)}$ jest największy równy $\frac{4}{3}$ .

Poszukajmy teraz wartości najmniejszej na krańcach przedziału $⟨0, 2⟩$ :

$f (0) = \frac{1}{0^{2} - 0 + 1} = 1$ i $f (2) = \frac{1}{2^{2} - 2 + 1} = \frac{1}{3}$ .

Odpowiedź

Funkcja przyjmuje wartość największą $\frac{4}{3}$ dla $x = \frac{1}{2}$ , a najmniejszą $\frac{1}{3}$ dla $x = 2$ .

Przykład 6

Funkcja kwadratowa $f$ przyjmuje w przedziale $⟨0, 3⟩$ największą wartość dla argumentów $0$ i $3$ . Parabola, będąca wykresem tej funkcji ma ramiona skierowane ku górze. Uzasadnimy, że w przedziale $⟨- 2, 5⟩$ funkcja $f$ przyjmuje największą wartość dla argumentów $- 2$ i $5$ .

Rozwiązanie

Funkcja kwadratowa $f$ przyjmuje w przedziale $⟨0, 3⟩$ największą wartość dla argumentów $0$ i $3$ . Oznacza to, że $f (0) = f (3)$ .

Ponadto otrzymujemy, że ramiona paraboli będącej wykresem funkcji $f$ są skierowane do góry oraz $x_{w} = \frac{0 + 3}{2} = 1, 5$ .

Osią symetrii wykresu funkcji $f$ jest prosta opisana wzorem $x = 1, 5$ oraz odległość argumentu $x = - 2$ od osi symetrii jest taka sama jak odległość argumentu $x = 5$ :

$|1, 5 - (- 2)| = |5 - 1, 5|$

$|3, 5| = |3, 5|$

$3, 5 = 3, 5$ .

Stąd otrzymujemy, że

$f (- 2) = f (5)$ .

Ponieważ ramiona paraboli są skierowane do góry, to w przedziale $⟨- 2, 5⟩$ funkcja $f$ przyjmuje największą wartość dla argumentów $- 2$ i $5$ .

Przykład 7

Fynkcja $f$ dana wzorem $f (x) = a x^{2} + b x + c$ określona w przedziale $⟨0, 4⟩$ , przyjmuje wartość najmniejszą dla $x = 2$ . Uzasadnimy, że $a > 0$ i $b < 0$ .

Rozwiązanie

Z treści zadania wiemy, że w przedziale $⟨0, 4⟩$ funkcja $f$ osiąga najmniejszą wartość dla argumentu $x = 2$ . Oznacza to, że ramiona paraboli, na której leży wykres funkcji $f$ są skierowane do góry ( $a > 0$ ) oraz jej wierzchołek leży na prostej $x = 2$ .

Zauważmy, że wzór na pierwszą współrzędną wierzchołka paraboli, to

$x_{w} = \frac{- b}{2 a}$ .

Korzystając z faktu, że wierzchołek znajduje się na prostej $x = 2$ dostajemy, że

$2 = \frac{- b}{2 a}$ .

Z powyższej równości wyznaczymy współczynnik $b$ .

$2 = \frac{- b}{2 a} / \cdot 2 a$

$4 a = - b$

Z wcześniejszych rozważań wiemy, że $a > 0$ . Stąd otrzymujemy, że

$- b > 0 \Leftrightarrow b < 0$ .

Słownik

funkcja kwadratowa

funkcja określona wzorem $f (x) = a x^{2} + b x + c$ dla wszystkich liczb rzeczywistych, gdzie $a$ , $b$ , $c$ są liczbami rzeczywistymi, przy czym $a \neq 0$

postać kanoniczna funkcji kwadratowej

$f (x) = a {(x - \frac{b}{2 a})}^{2} - \frac{Δ}{4 a}$ , gdzie $x_{w} = - \frac{b}{2 a}$ , $y_{w} = - \frac{Δ}{4 a}$ i $Δ = b^{2} - 4 a c$

Wprowadzenie

Animacja

Słownik