Przeczytaj

W materiale omówimy zależność, jaka występuje pomiędzy polami trójkątów podobnych.

Jeżeli trójkąty mają ustalone nazwy wierzchołków, to podobieństwo tych trójkątów zapisujemy symbolicznie $△ A B C ~ △ A' B' C'$ .

RfVX0UeCX7oe9

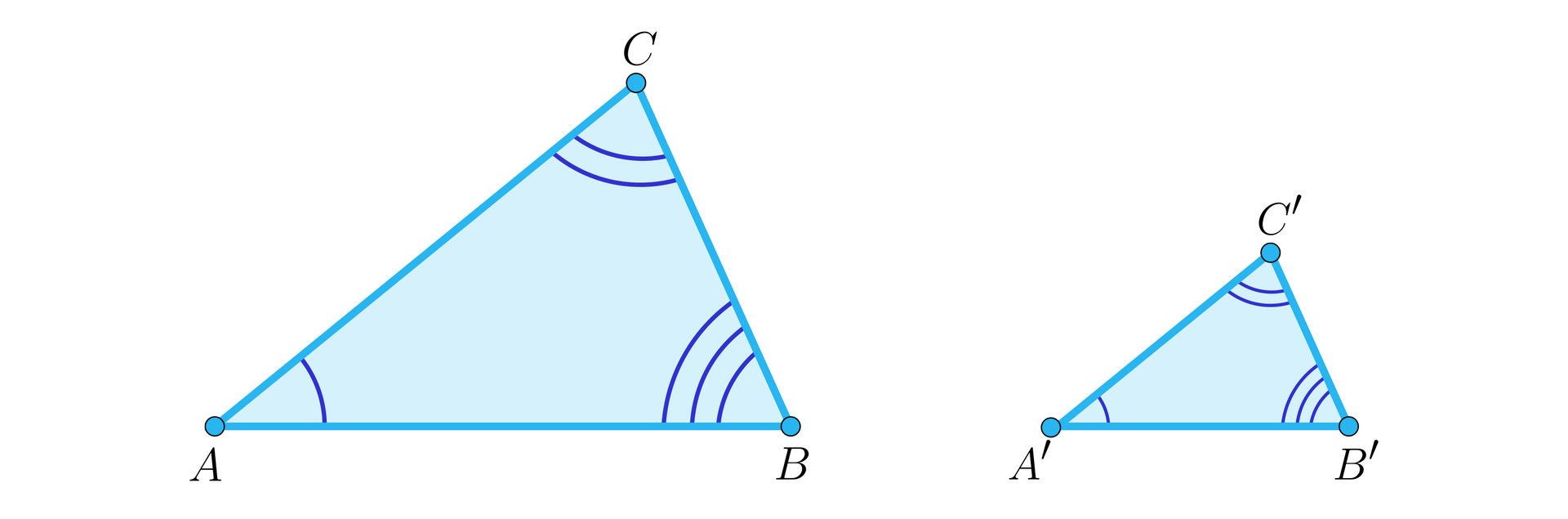
Ilustracja przedstawia dwa trójkąty jeden A B C, a drugi A prim B prim C prim. Jednym łukiem został zaznaczony kąt przy wierzchołku A oraz A prim. Dwoma łukami kąt przy wierzchołku C oraz C prim. A trzema łukami został oznaczony kąt przy wierzchołku B oraz B prim.

Trójkąty są podobnetrójkąty podobneTrójkąty są podobne, gdy zachodzi jeden z poniższych warunków:

długości boków jednego trójkąta są proporcjonalne do długości odpowiednich boków drugiego trójkąta,
trójkąty mają takie same kąty,
długości dwóch boków jednego trójkąta są proporcjonalne do długości odpowiednich dwóch boków drugiego trójkąta, a kąty między tymi bokami są równej miary.

Wymienione warunki nazywamy cechami podobieństwa trójkątówcechy podobieństwa trójkątówcechami podobieństwa trójkątów.

Na rysunku przedstawiono trójkąty podobne z zaznaczonymi długościami boków oraz obwodami.

RpoH5NTKXVv0m

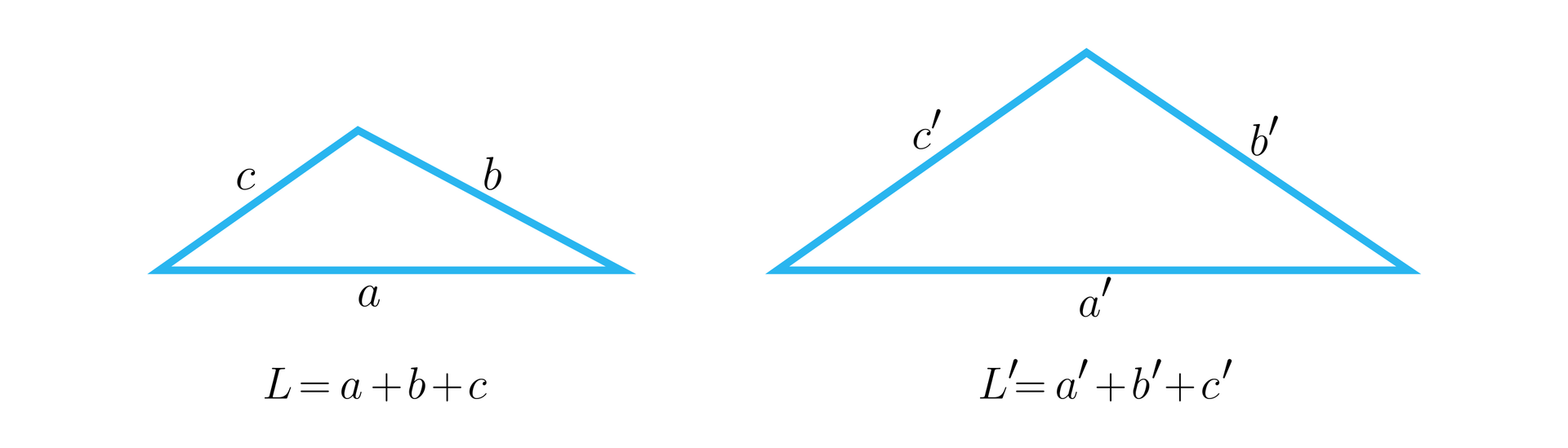
Ilustracja przedstawia dwa trójkąty. Pierwszy o bokach a b oraz c. Obwód pierwszego trójkąta zapisano równaniem L=a+b+c. Drugi o bokach a prim b prim c prim. Obwód drugiego trójkąta zapisano równaniem L=a'+b'+c'

Jeżeli przez $k$ oznaczymy skalę podobieństwa tych trójkątów, to:

$k = \frac{a'}{a} = \frac{b'}{b} = \frac{c'}{c}$ ,

$k = \frac{L'}{L}$ .

pola trójkątów podobnych

Twierdzenie: pola trójkątów podobnych

Stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa tych trójkątów.

Dowód

Narysujmy dwa trójkąty, które są podobne w skali $k$ , gdzie $k > 0$ . Wprowadźmy oznaczenia, jak na rysunkach:

R1dPMLa1zbYwU

Ilustracja przedstawia dwa trójkąty. Pierwszy o podstawie o długości a i wysokości h upuszczonej na tą podstawę. Drugi o podstawie a prim i wysokości h upuszczonej na tą podstawę.

Jeżeli trójkąty są podobne w skali $k$ , to ich odpowiednie boki oraz wysokości są proporcjonalne.

Zatem:

$k = \frac{a'}{a}$ , więc $a' = k \cdot a$ ,

$k = \frac{h'}{h}$ , więc $h' = k \cdot h$ .

Oznaczmy pole mniejszego trójkąta jako $P$ , a większego jako $P'$ .

Wówczas, stosując oznaczenia z rysunków otrzymujemy:

$P = \frac{1}{2} \cdot a \cdot h$ ,

$P' = \frac{1}{2} \cdot a' \cdot h'$ .

Zatem:

$\frac{P'}{P} = \frac{\frac{1}{2} \cdot a' \cdot h'}{\frac{1}{2} \cdot a \cdot h} = \frac{\frac{1}{2} \cdot k \cdot a \cdot k \cdot h}{\frac{1}{2} \cdot a \cdot h} = k^{2}$ .

Przykład 1

Stosunek pól trójkątów podobnych $K L M$ oraz $K' L' M'$ wynosi $\frac{9}{16}$ . Wiedząc, że długość podstawy $K L$ trójkąta $K L M$ jest o $4$ mniejsza od długości podstawy $K' L'$ , obliczymy długości tych podstaw.

RUoF3Zqa8ZS8q

Ilustracja przedstawia trójkąty podobne KLM oraz k prim l prim m prim.

Rozwiązanie:

Jeżeli przez $k$ oznaczymy skalę podobieństwa tych trójkątów oraz zapiszemy $|K' L'| = |K L| + 4$ , to:

$k^{2} = \frac{9}{16}$ , zatem $k = \frac{3}{4}$ .

Zauważmy, że $k = \frac{|K L|}{|K' L'|}$ , zatem $\frac{3}{4} = \frac{|K L|}{|K L| + 4}$ .

Z równania otrzymujemy, że $|K L| = 12$ , zatem $|K' L'| = 16$ .

Przykład 2

Obwód trójkąta $A B C$ wynosi $72$ , a jego pole $144$ . Obwód trójkąta $A' B' C'$ do niego podobnego wynosi $18$ . Obliczymy pole trójkąta $A' B' C'$ .

Rozwiązanie:

Ponieważ trójkąty $A B C$ oraz $A' B' C'$ są podobne, zatem:

$k = \frac{L_{A B C}}{L_{A' B' C'}} = \frac{72}{18} = 4$ .

Korzystając z faktu, że stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa otrzymujemy, że:

$k^{2} = \frac{P_{A B C}}{P_{A' B' C'}}$ , więc $4^{2} = \frac{144}{P_{A' B' C'}}$ .

Zatem $P_{A' B' C'} = 9$ .

Przykład 3

Suma pól dwóch trójkątów podobnych jest równa $270$ , a skala podobieństwa tych trójkątów wynosi $k = 3$ . Wyznaczymy pole każdego z tych trójkątów.

Rozwiązanie:

Wprowadźmy oznaczenia:

$P_{1}$ – pole pierwszego trójkąta,

$P_{2}$ – pole drugiego trójkąta.

Jeżeli skala podobieństwa tych trójkątów wynosi $k = 3$ , to do wyznaczenia pola każdego z tych trójkątów rozwiążemy układ równań:

$\{\begin{cases} P_{1} + P_{2} = 270 \\ \frac{P_{1}}{P_{2}} = 3^{2} \end{cases}$

Z drugiego równania wynika, że $P_{1} = 9 \cdot P_{2}$ , zatem:

$9 \cdot P_{2} + P_{2} = 270$ , czyli $P_{2} = 27$ .

$P_{1} = 9 \cdot P_{2} = 9 \cdot 27 = 243$ .

Pola tych trójkątów wynoszą $243$ i $27$ .

Zależność pomiędzy polami trójkątów podobnych możemy wykorzystać do obliczania pól innych figur.

Przykład 4

Wyznaczymy pole trapezu $A B C D$ przedstawionego na rysunku, jeżeli wiadomo, że pola trójkątów $A B S$ oraz $S C D$ wynoszą odpowiednio $28$ i $7$ .

RTccIudvmtLXo

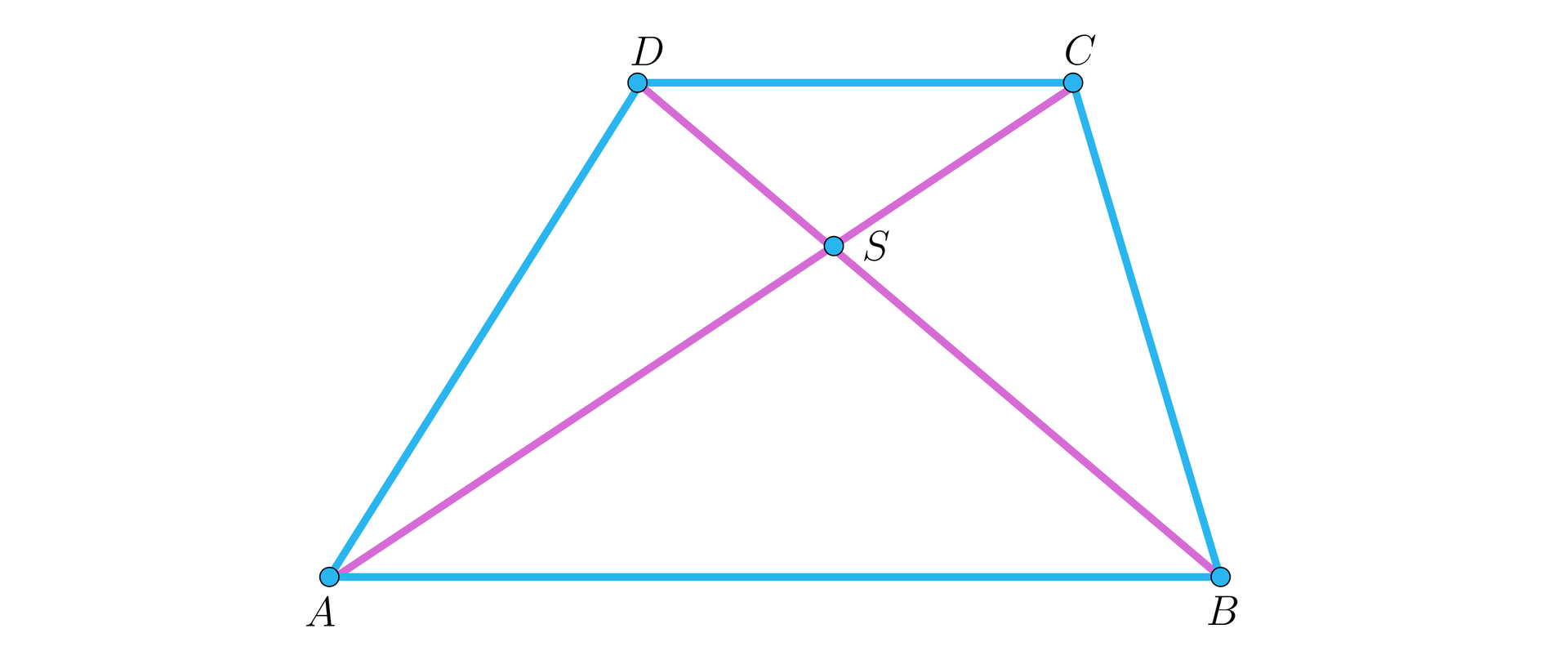
Ilustracja przedstawia trapez A B C D. Przekątne trapezu przecinają się w punkcie S.

Rozwiązanie:

Zauważmy, że trójkąty $A B S$ oraz $S C D$ są podobne, ponieważ mają takie same kąty.

RQX55zLnFbyq7

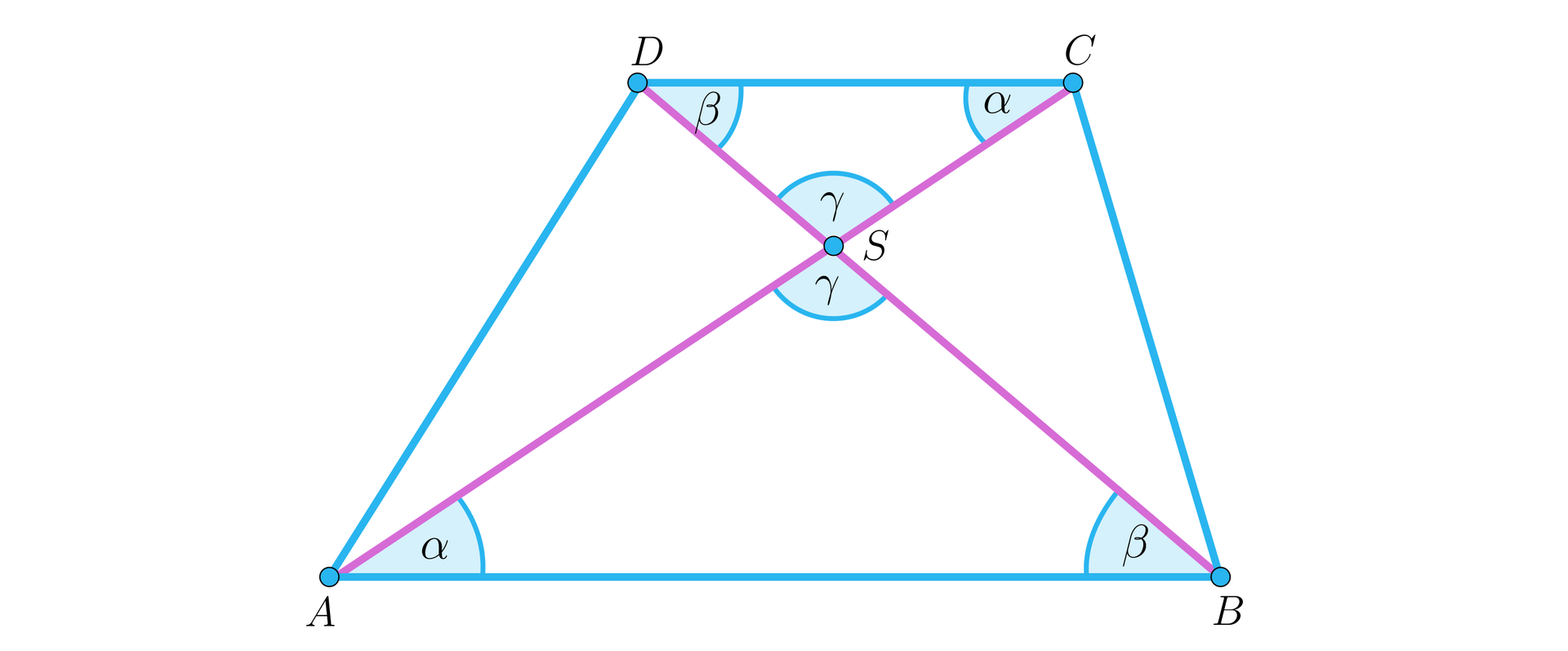
Ilustracja przedstawia trapez A B C D. Przekątne trapezu przecinają się w punkcie S. Kąt pomiędzy przekątną a wierzchołkiem A oraz C ma miarę alfa. Kąt pomiędzy wierzchołkiem B oraz D ma miarę beta. Kąty wierzchołkowe na przecięciu przekątnych maja miarę gamma.

Zatem $k^{2} = \frac{P_{A B S}}{P_{S C D}} = \frac{28}{7} = 4$ , więc skala podobieństwa tych trójkątów wynosi $2$ .

Podstawy i wysokości trójkątów $A B S$ oraz $S C D$ pozostają zatem w stosunku $2 : 1$ .

Wprowadźmy oznaczenia, jak na poniższym rysunku.

Riow1TLeuhZej

Ilustracja przedstawia trapez A B C D. Przekątne trapezu przecinają się w punkcie S. Ze środka górnej podstawy DC o długości a upuszczono wysokość na dolną podstawę 2 a. Długość wysokości od górnej podstawy do punktu S ma miarę h, a długość od dolnej podstawy do punktu S ma miarę 2h.

Zgodnie z oznaczeniami mamy:

$P_{S C D} = \frac{1}{2} \cdot a \cdot h$ , czyli $7 = \frac{1}{2} \cdot a \cdot h$ , więc $a \cdot h = 14$ .

$P_{A B C D} = \frac{(2 a + a) \cdot 3 h}{2} = \frac{9 \cdot a \cdot h}{2} = \frac{9 \cdot 14}{2} = 63$ .

Pole trapezu $A B C D$ wynosi $63$ .

Przykład 5

Obliczymy długość przeciwprostokątnej trójkąta prostokątnego, jeśli wysokość poprowadzona z wierzchołka kąta prostego podzieliła ten trójkąt na dwa trójkąty o polach $81$ i $225$ .

Rozwiązanie:

Narysujmy trójkąt prostokątny i wprowadźmy oznaczenia, jak na poniższym rysunku.

R157L4dvGIQPV

Ilustracja przedstawia trójkąt A B C. Przekątna upuszczona z wierzchołka A na przeciwprostokątną ma miarę h. Tworzy ona z nią punkt D, który dzieli przeciwprostokątną na dwa odcinki x oraz y. Powstały dwa trójkąty. Pierwszy A C D o polu równym 81 jednostek oraz drugi A B D o polu równym 225

Trójkąty $A B D$ oraz $A D C$ są podobne (ich odpowiednie kąty są równe), zatem zachodzi zależność:

$\frac{h}{x} = \frac{y}{h}$ , czyli $h^{2} = x y$

Pola trójkątów $A B D$ oraz $A D C$ obliczamy ze wzorów:

$P_{A B D} = \frac{1}{2} \cdot y \cdot h$

$P_{A D C} = \frac{1}{2} \cdot x \cdot h$

Zatem $\frac{1}{2} \cdot x \cdot h = 81$ oraz $\frac{1}{2} \cdot y \cdot h = 225$ .

Zauważmy, że $\frac{\frac{1}{2} \cdot x \cdot h}{\frac{1}{2} \cdot y \cdot h} = \frac{81}{225}$ .

Wobec tego $\frac{x}{y} = \frac{9}{25}$ , czyli $y = \frac{25}{9} x$ .

Po przekształceniu mamy: $x \cdot h = 162$ , czyli $h = \frac{162}{x}$ .

Po podstawieniu zależności $h = \frac{162}{x}$ oraz $y = \frac{25}{9} x$ do równania $h^{2} = x y$ , rozwiązujemy równanie z niewiadomą $x$ :

${(\frac{162}{x})}^{2} = x \cdot (\frac{25}{9} x)$

$\frac{26244}{x^{2}} = \frac{25}{9} x^{2}$

$x^{4} = \frac{9 \cdot 26244}{25}$

Ponieważ $x > 0$ , zatem $x = \frac{\sqrt{3} \cdot 9 \sqrt{2}}{\sqrt{5}} = \frac{9 \sqrt{6}}{\sqrt{5}} = \frac{9 \sqrt{30}}{5}$ .

Długość przeciwprostokątnej $B C$ wynosi:

$|B C| = x + \frac{25}{9} x = \frac{34}{9} x$

Wobec tego

$|B C| = \frac{34}{9} \cdot \frac{9 \sqrt{30}}{5} = \frac{34 \sqrt{30}}{5}$

Przykład 6

W trójkącie prostokątnym $A B C$ przyprostokątne $A B$ i $A C$ mają odpowiednio długości $a \sqrt{2}$ i $a$ . Na przyprostokątnej $A B$ wybrano taki punkt $P$ , że $|∢ A P C| = |∢ A C B|$ . Obliczymy pola trójkątów $A P C$ i $P B C$ .

Rozwiązanie:

Narysujmy trójkąt prostokątny i wprowadźmy odpowiednie oznaczenia.

Rsqgb7CDVT8Bh

Ilustracja przedstawia trójkąt prostokątny A B C o podstawie równej a2 oraz wysokości równej a. Z wierzchołka C upuszczono odcinek na podstawę tworząc punkt P.

Zauważmy, że trójkąty $A P C$ i $A B C$ są podobne na podstawie cechy podobieństwa $k k k$ .

Pole trójkąta $A B C$ wynosi:

$P_{A B C} = \frac{1}{2} \cdot a \cdot a \sqrt{2} = \frac{a^{2} \sqrt{2}}{2}$

Jeżeli $k$ jest skalą podobieństwa trójkąta $A P C$ do trójkąta $A B C$ , to:

$k = \frac{|A C|}{|A B|} = \frac{a}{a \sqrt{2}} = \frac{\sqrt{2}}{2}$

Ponieważ stosunek pól trójkątów podobnych jest równy kwadratowi skali ich podobieństwa, zatem:

$P_{A P C} = k^{2} \cdot P_{A B C} = {(\frac{\sqrt{2}}{2})}^{2} \cdot \frac{a^{2} \sqrt{2}}{2} = \frac{a^{2} \sqrt{2}}{4}$

oraz

$P_{P B C} = P_{A B C} - P_{A P C} = \frac{a^{2} \sqrt{2}}{2} - \frac{a^{2} \sqrt{2}}{4} = \frac{a^{2} \sqrt{2}}{4}$

Słownik

trójkąty podobne

trójkąty, w których odpowiednie boki są parami proporcjonalne, a kąty między tymi bokami są równe

cechy podobieństwa trójkątów

warunki konieczne i wystarczające, aby dwa trójkąty były podobne

Wprowadzenie

Aplet

Słownik