Przeczytaj
Teraz utrwalisz wiadomości o kątach między odcinkami w graniastosłupie prawidłowym sześciokątnym oraz rozwiniesz zdobyte wcześniej umiejętności i zastosujesz je do rozwiązywania bardziej złożonych zagadnień.
Pojęcia wstępne
Kąty między przekątnymi podstawy graniastosłupa prawidłowego sześciokątnego

Do ciekawszych kątów, które da się zaobserwować w podstawie należą:
kątkąt między krótszą i dłuższą przekątną wychodzącymi z jednego wierzchołka ,
kąt między dwiema krótszymi przekątnymi wychodzącymi z jednego wierzchołka ,
kąt przecięcia między dwiema krótszymi przekątnymi wychodzącymi z kolejnych wierzchołków .
Kąty między przekątnymi graniastosłupa prawidłowego sześciokątnego a przekątnymi jego podstawy
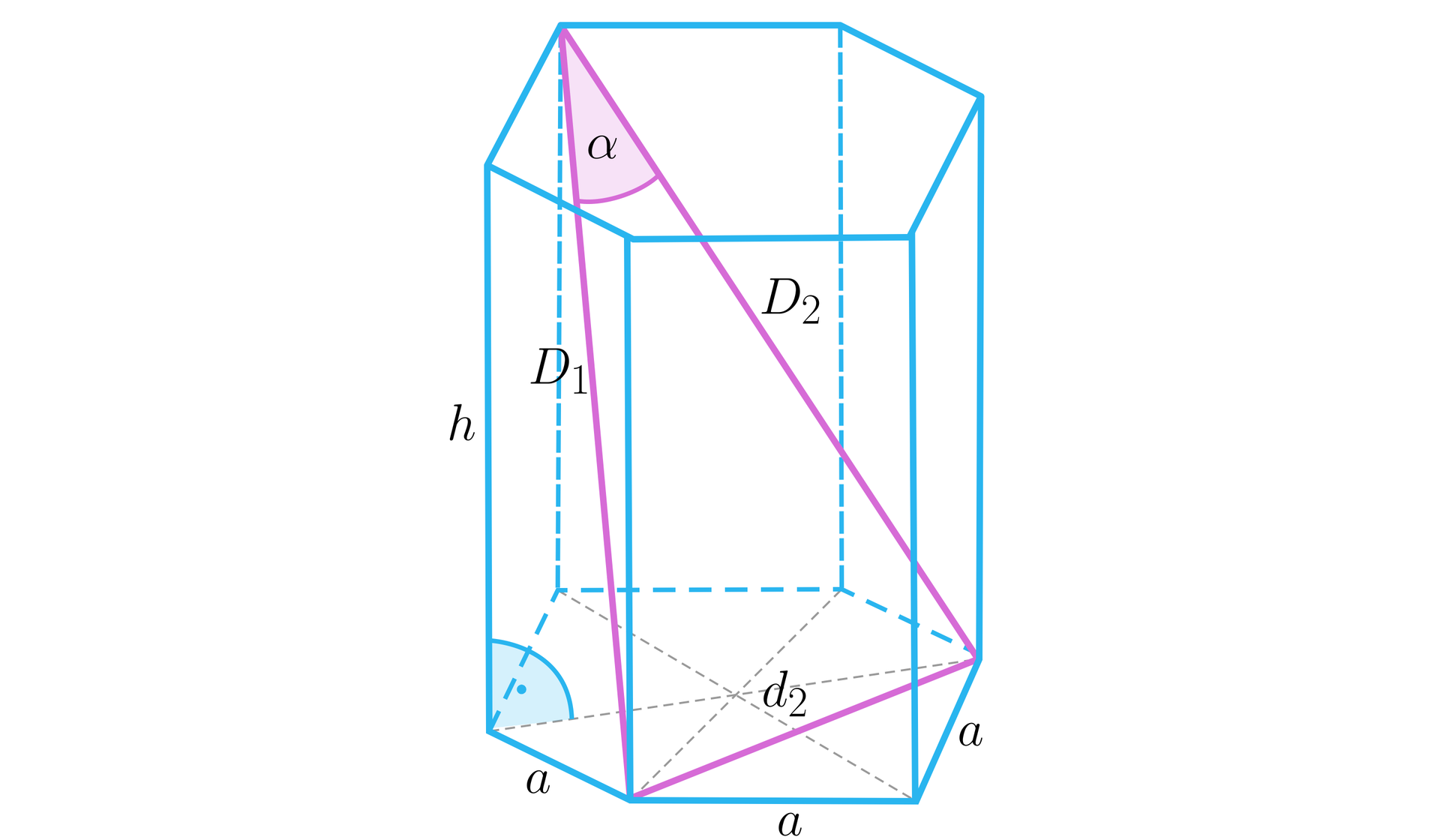
Przeanalizujemy dane umieszczone na rysunku.
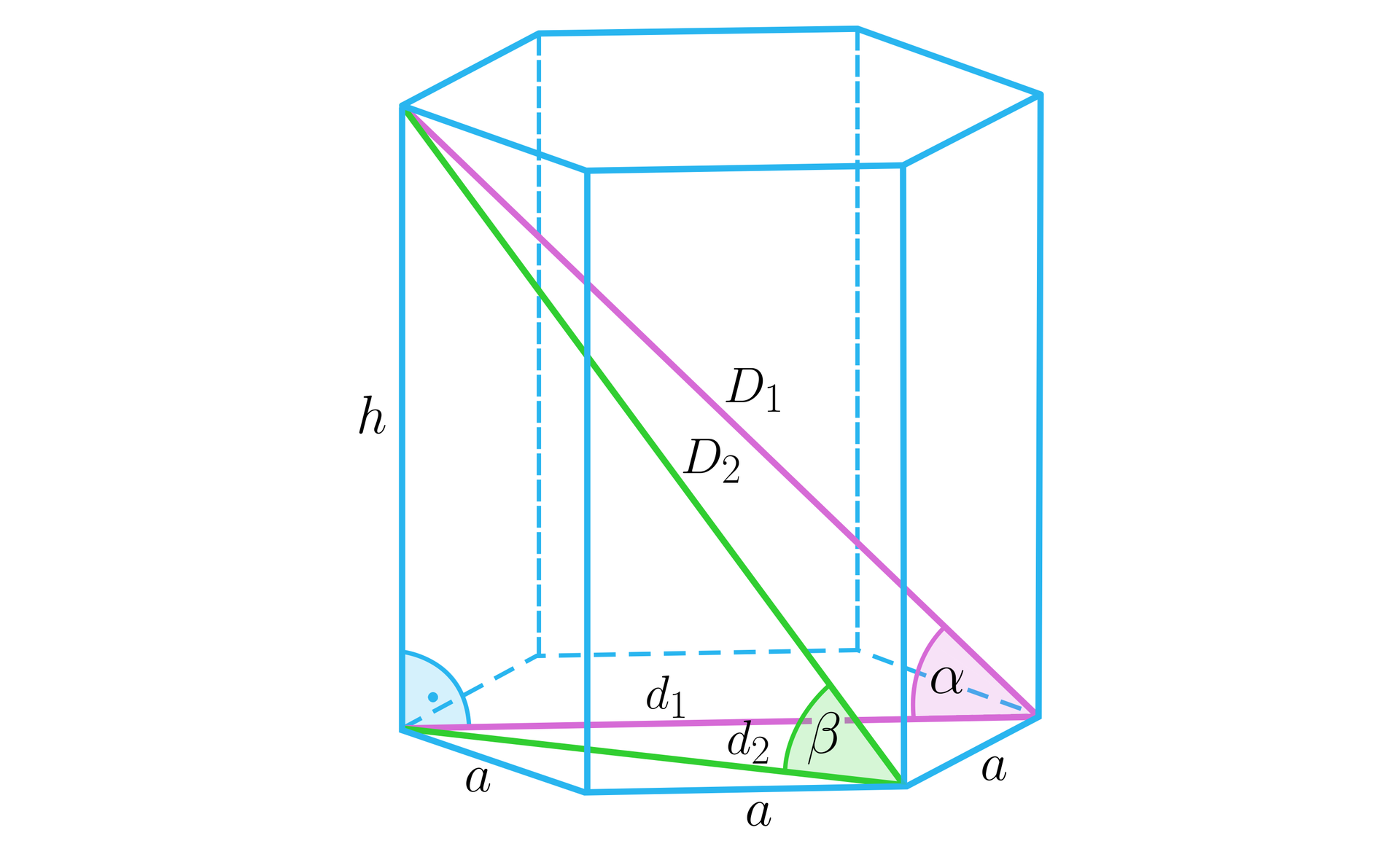
Kąty i są kątami ostrymi oraz .
Wysokość graniastosłupa przedstawiona na dwa sposoby w zależności od kąta i :
z czego wynika, że między kątami i zachodzi następujący związek:
Długości przekątnych graniastosłupa wyrażają się wzorami:
oraz między kątami ostrymi i zachodzi następujący związek:
Kąty między przekątnymi sąsiednich ścian bocznych graniastosłupa prawidłowego sześciokątnego
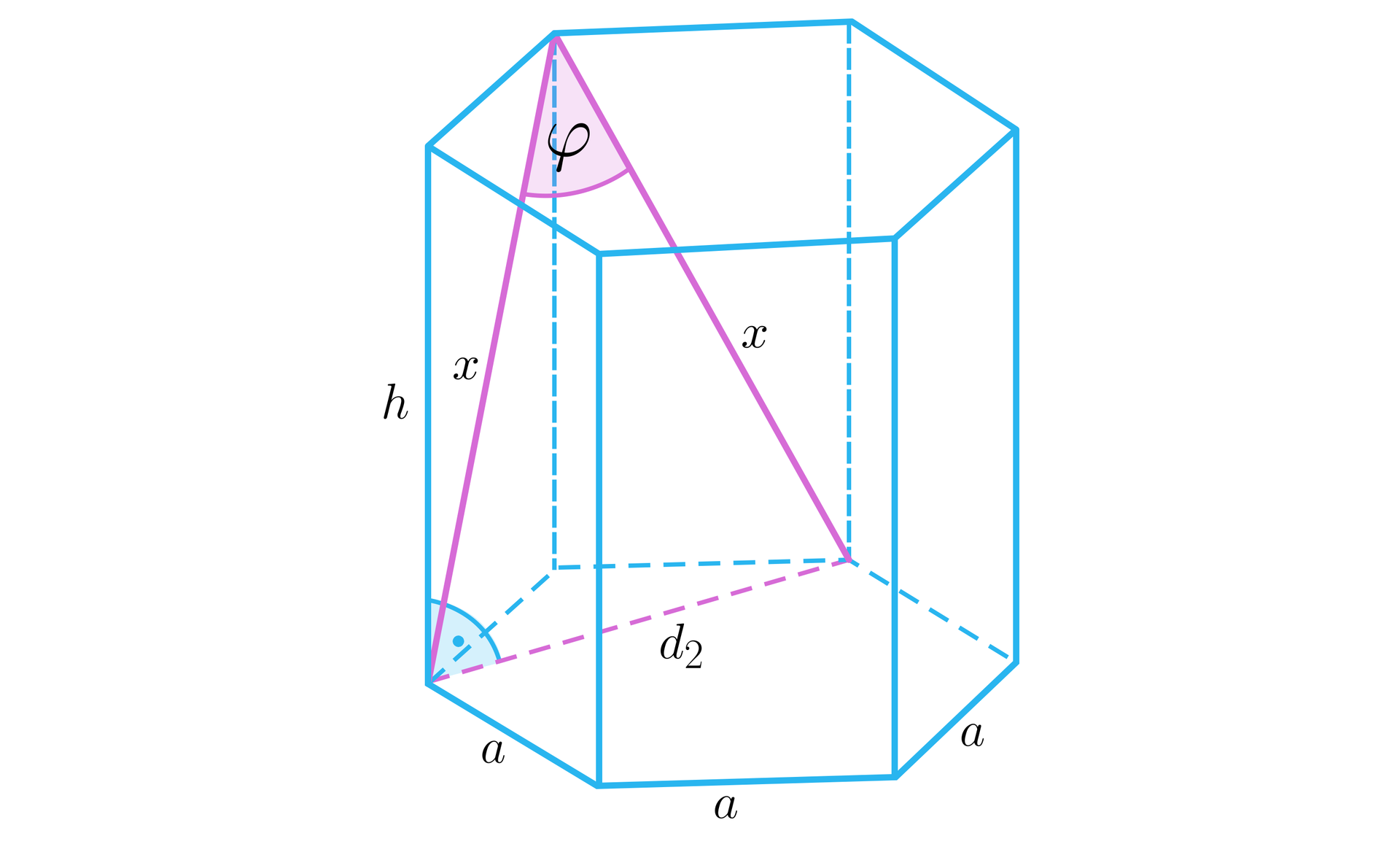
- kąt między przekątnymi sąsiednich ścian bocznych graniastosłupa prawidłowego sześciokątnego
Kąty między przekątnymi graniastosłupa prawidłowego sześciokątnego wychodzącymi z jednego wierzchołka
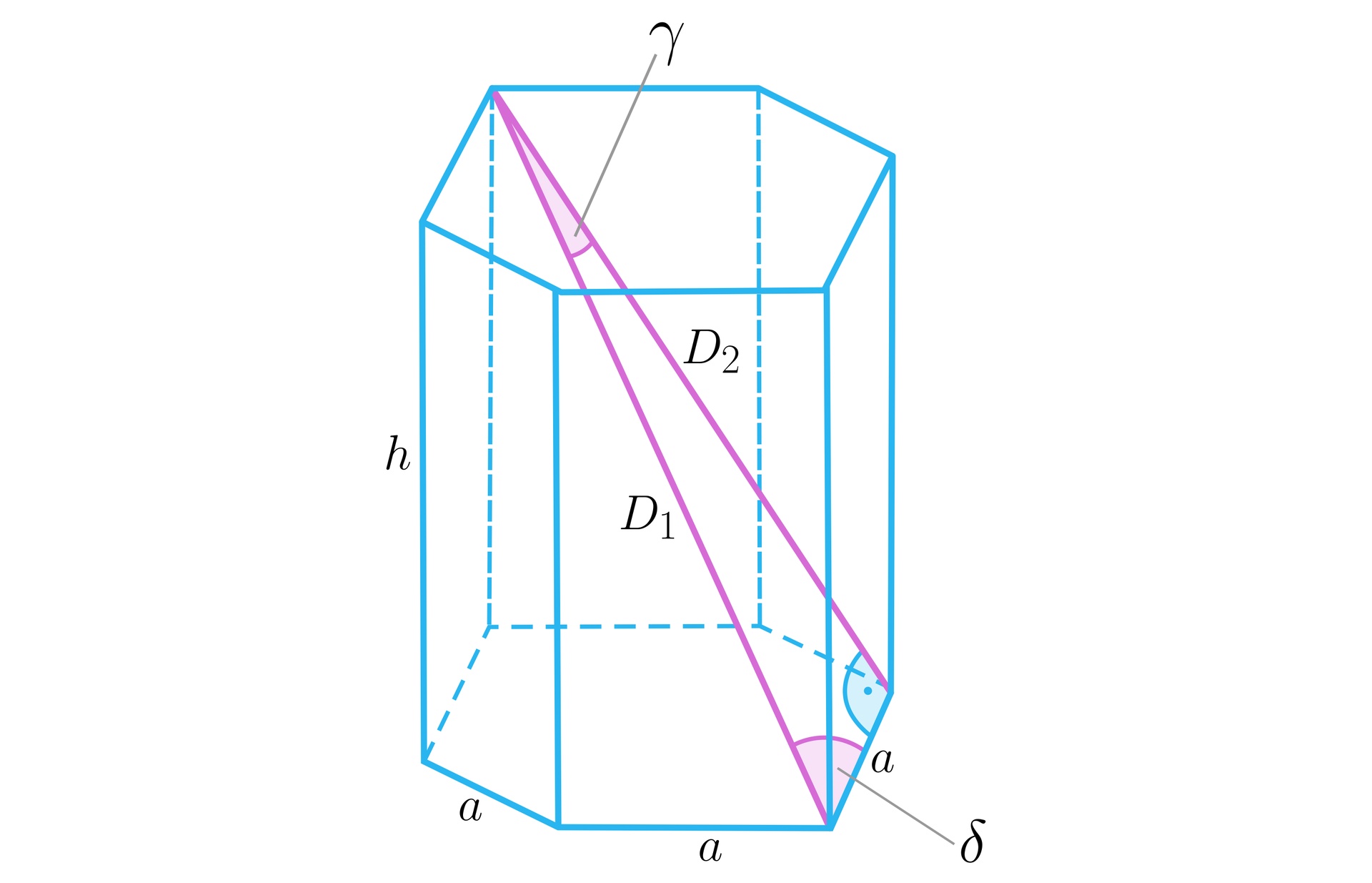
- kąt między dłuższą i krótszą przekątną graniastosłupaprzekątną graniastosłupa poprowadzonymi z jednego wierzchołka
- kąt między dłuższą przekątną graniastosłupa a krawędzią podstawy
Dłuższa przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość i tworzy z jedną z przekątnych tego graniastosłupa kąt . Wyznaczymy sumę długości krawędzi w tym graniastosłupie oraz długości jego przekątnych.
Rozwiązanie
W zadaniu musimy rozważyć dwa przypadki, ponieważ badany graniastosłup posiada dwie przekątne i różnej długości.
Przypadek I
Na początku zbadamy dłuższą przekątną graniastosłupa.

W zadaniu mamy dane dwie wielkości - przekątną podstawy oraz kąt ostry .
Od razu można wyznaczyć długość krawędzi podstawy i wysokość graniastosłupa .
Szukana suma długości krawędzi wynosi:
.
Natomiast przekątne wyrażają się wzorami:
Odpowiedź: Suma krawędzi wynosi , a przekątne i .
Przypadek II
Następnie zbadamy krótszą przekątną graniastosłupa.

W zadaniu mamy dane dwie wielkości - przekątną podstawy oraz kąt ostry , stąd krawędzi podstawy .
Wyznaczymy teraz wysokość graniastosłupa w zależności oddanych wielkości i .
Rozważymy wyróżniony trójkąt:

Wykorzystując własności trapezu równoramiennego wyliczmy odcinki:
oraz .
Następnie , stąd stosując twierdzenie Pitagorasa mamy odcinek , :
.
Odcinek jest przekątną prostokąta w ścianie bocznej możemy, więc wyliczyć wysokość ,
przy założeniu, że ,
czyli .
Szukana suma krawędzi wynosi:
,
dla .
Natomiast przekątne wynoszą:
Odpowiedź: Suma krawędzi wynosi , a przekątne i ,
wyrażenia istnieją dla .
Dany jest graniastosłup prawidłowy sześciokątny, którego ścianami bocznymi są kwadraty. Sprawdzimy, czy któryś z kątów pomiędzy zaznaczonymi na rysunku odcinkami jest prosty. Uzasadnimy odpowiedź.
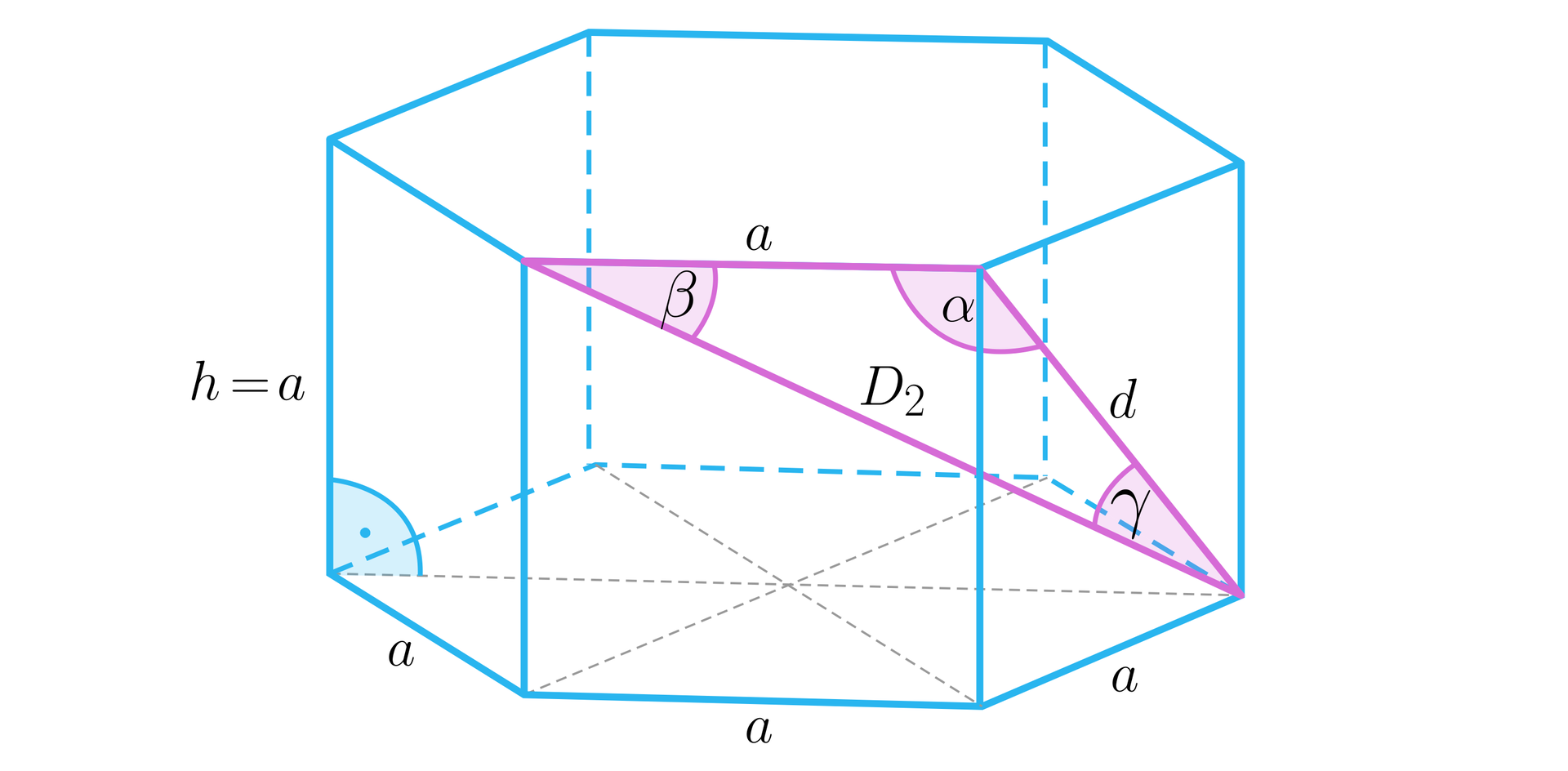
Rozwiązanie
Niech .
Odcinek jest przekątną ściany bocznej, krótsza przekątna graniastosłupa wynosi:
.
Wyznaczymy jeden z kątów w powstałym trójkącie z twierdzenia kosinusów:
.
Odpowiedź: Jeden z kątów jest kątem rozwartym, więc badany trójkąt nie może być prostokątny, więc żaden z kątów nie wynosi .
Wyznaczymy kąt między krótszymi przekątnymi wychodzącymi z jednego wierzchołka w graniastosłupie prawidłowym sześciokątnym, w którym wysokość jest
a) dwa razy większa od krawędzi podstawy,
b) , razy większa od krawędzi podstawy, gdzie jest dowolną liczbą dodatnią.
Rozwiązanie
a)
Na rysunku zaznaczono badany kąt .
Wiemy, że , stąd .
Natomiast .
Wyznaczymy szukany kąt stosując twierdzenie kosinusów:
.
Odpowiedź: Szukany kąt wynosi .
b)
Analogicznie do podpunktu a) widzimy, że , stąd , natomiast .
Wyznaczymy szukany kąt stosując twierdzenie kosinusów:
.
przybliżoną wartość odczytujemy z tablic matematycznych.
Słownik
przekątną graniastosłupa nazywamy każdy odcinek, którego końcami są wierzchołki obu podstaw graniastosłupa i który nie zawiera się w żadnej ze ścian graniastosłupa
płaszczyzna zawarta między dwiema półprostymi wychodzącymi z tego samego punktu. Punkt, który łączy obie półproste to wierzchołek kąta. Dwie półproste stanowią ramiona kąta