Wielomiany mają postać ogólną: $W\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_2{x}^2+a_{1}x+a_0$, gdzie: $a_n,\dots ,a_0$ nazywamy współczynnikami wielomianu, a $a_0$ wyrazem wolnym.

Dane są wielomiany $F\left(x\right)$ i $G\left(x\right)$.

• Sumą wielomianów $F\left(x\right)$ i $G\left(x\right)$ nazywamy taki wielomian $W\left(x\right)$, że dla każdej liczby rzeczywistej $a$ spełniony jest warunek

Wyznaczymy sumę wielomianów $F\left(x\right)=6x^4+5x^2-2x-8$ oraz $G\left(x\right)=7x^5-4x^4+2x^3-5x$ i przedstawimy wynik w postaci uporządkowanej sumy algebraicznej.

Rozwiązanie

Gdy dodajemy dwa wielomiany, redukujemy wyrazy podobne, czyli dodajemy współczynniki stojące przed zmienną $x$ w tej samej potędze. Rozważaną sumę zapisujemy:

$W\left(x\right)=F\left(x\right)+G\left(x\right)=6x^4+5x^2-2x-8+7x^5-4x^4+2x^3-5x=$$=7x^5+2x^4+2x^3+5x^2-7x-8$.

Szukany wielomian jest postaci $W\left(x\right)=7x^5+2x^4+2x^3+5x^2-7x-8$.

• Różnicą wielomianów $F\left(x\right)$ i $G\left(x\right)$ nazywamy taki wielomian $W\left(x\right)$, że dla każdej liczby rzeczywistej $a$ spełniony jest warunek

Wyznaczamy różnicę wielomianów $F\left(x\right)=10x^4-x^3+6x^2-1$ oraz $G\left(x\right)=6x^5-17x^4+12x^2-4$ i przedstawiamy wynik w postaci uporządkowanej sumy algebraicznej.

Rozwiązanie

Gdy odejmujemy dwa wielomiany, redukujemy wyrazy podobne, czyli odejmujemy współczynniki stojące przed zmienną $x$ w tej samej potędze. Rozważaną różnicę zapisujemy:

$W\left(x\right)=F\left(x\right)-G\left(x\right)=10x^4-x^3+6x^2-1-\left(6x^5-17x^4+12x^2-4\right)=$$=10x^4-x^3+6x^2-1-6x^5+17x^4-12x^2+4=-6x^5+27x^4-x^3-6x^2+3$.

Szukany wielomian jest postaci $W\left(x\right)=-6x^5+27x^4-x^3-6x^2+3$.

• $\text{deg}\left(W\left(x\right)+P\left(x\right)\right)⩽\text{max}\left(\text{deg}\left(W\left(x\right)\right),\text{deg}\left(P\left(x\right)\right)\right)$ lub $W\left(x\right)+P\left(x\right)$ jest wielomianem zerowym.

• $\text{deg}\left(W\left(x\right)-P\left(x\right)\right)⩽\text{max}\left(\text{deg}\left(W\left(x\right)\right),\text{deg}\left(P\left(x\right)\right)\right)$ lub $W\left(x\right)-P\left(x\right)$ jest wielomianem zerowym.

Dane są wielomiany $F\left(x\right)$ i $G\left(x\right)$. Iloczynem wielomianów $F\left(x\right)$ i $G\left(x\right)$ nazywamy taki wielomian $W\left(x\right)$, że dla każdej liczby $a\in \mathrm{ℝ}$ spełniony jest warunek:

Pomnóż wielomiany $F\left(x\right)=3x^4-2x^3+x$ oraz $G\left(x\right)=x^3-2x^4+1$ i przedstaw wynik w postaci uporządkowanej sumy algebraicznej.

Rozwiązanie

Wyznaczymy iloczyn podanych wielomianów, mnożąc każdy współczynnik pierwszego wielomianu przez każdy współczynnik drugiego wielomianu. Rozważany iloczyn zapisujemy:

$W\left(x\right)=F\left(x\right)·G\left(x\right)=\left(3x^4-2x^3+x \right)·\left(x^3-2x^4+1\right)=$$=3x^7-6x^8+3x^4-2x^6+4x^7-2x^3+x^4-2x^5+x=$$=-6x^8+7x^7-2x^6-2x^5-2x^3+4x^4+x$.

Zatem szukany wielomian jest postaci $W\left(x\right)=-6x^8+7x^7-2x^6-2x^5+4x^4-2x^3+x$.

• Jeżeli $F\left(x\right)$ i $G\left(x\right)$ nie są wielomianami zerowymi, to $\text{deg}\left(F\left(x\right)·G\left(x\right)\right)=\text{deg}\left(F\left(x\right)\right)+\text{deg}\left(G\left(x\right)\right)$.

• Jeżeli $F\left(x\right)$ lub $G\left(x\right)$ jest wielomianem zerowym, to $F\left(x\right)·G\left(x\right)$ jest wielomianem zerowym.

Wielomian $W\left(x\right)$ jest podzielny przez niezerowy wielomian $F\left(x\right)$ wtedy i tylko wtedy, gdy istnieje wielomian $G\left(x\right)$ taki, że $W\left(x\right)=F\left(x\right)·G\left(x\right)$.

Wykonamy dzielenie wielomianu $W\left(x\right)=12x^5-4x^4-30x^3+4x^2+15$ przez wielomian $F\left(x\right)=2x^2-5$.

Rozwiązanie

R13uDEFHst27Y

Ilustracja przedstawia dzielenie pisemne wielomianów $12x^5-4x^4-30x^3+4x^2+15$ oraz $2x^2-5$, nad działaniem znajduje się pozioma linia wyniku, pod działaniem zapisujemy wyniki dzielenia. Rozważmy pierwszy składnik dzielnej, czyli $12x^5$ i dzielimy go przez pierwszy składnik dzielnika, czyli $2x^2$, nad linią wyniku nad $12x^5$ zapisujemy $6x^3$, następnie mnożymy $6x^3$ razy $2x^2$ i wynik $12x^5$ z przeciwnym znakiem zapisujemy pod pierwszym składnikiem dzielnej, następnie mnożymy $6x^3$ razy minus pięć i wynik $-30x^3$ z przeciwnym znakiem zapisujemy pod składnikiem dzielnej zawierającej x do potęgi trzeciej, czyli pod $-30x^3$. Pod tym kreślimy pionową linię i dokonujemy odejmowania $12x^5$ odjąć $12x^5$, czyli zero. Tego wyniku nie zapisujemy pod kreską tylko przepisujemy kolejny składnik dzielnej $-4x^4$, dokonujemy dodawania składników $-30x^3$ oraz $30x^3$, otrzymujemy zero , którego nie zapisujemy pod kreską, tylko przepisujemy dwa ostatnie składniki dzielnej, czyli $4x^2+15$. Otrzymujemy $-4x^4+4x^2+15$, dzielimy pierwszy składnik tej sumy przez $2x^2$ i wynik $-2x^2$ zapisujemy nad linią wyniku nad $-4x^4$, następnie mnożymy $-2x^2$ razy $2x^2$ i wynik $-4x^4$ zapisujemy pod $-4x^4$ z przeciwnym znakiem, dalej mnożymy $-2x^2$ razy minus pięć i wynik $10x^2$ zapisujemy z przeciwnym znakiem pod $4x^2$. Kreślimy pionową linię. Dokonujemy dodawania składników $-4x^4$ oraz $4x^4$ i otrzymujemy zero, czego nie zapisujemy pod pionową linią, następnie odejmujemy od $4x^2$ $10x^2$ i wynik $-6x^2$ zapisujemy pod pionową linią, przepisujemy plus piętnaście. Zatem rozważamy teraz sumę postaci $-6x^2+15$, pierwszy składnik sumy dzielimy przez $2x^2$ i wynik minus trzy zapisujemy nad linią wyniku nad $-30x^3$, następnie mnożymy minus trzy razy $2x^2$ i wynik $-6x^2$ zapisujemy pod pierwszym składnikiem sumy z przeciwnym znakiem, dalej mnożymy minus trzy razy minus pięć i zapisujemy wynik piętnaście z przeciwnym znakiem pod drugim składnikiem sumy, kreślimy pionową kreskę i dodajemy $-6x^2$ i $6x^2$ z czego otrzymujemy zero oraz odejmujemy do piętnastu piętnaście i otrzymujemy również zero. Zatem pod kreską zapisujemy zero, czyli wielomian podzielił się bez reszty.

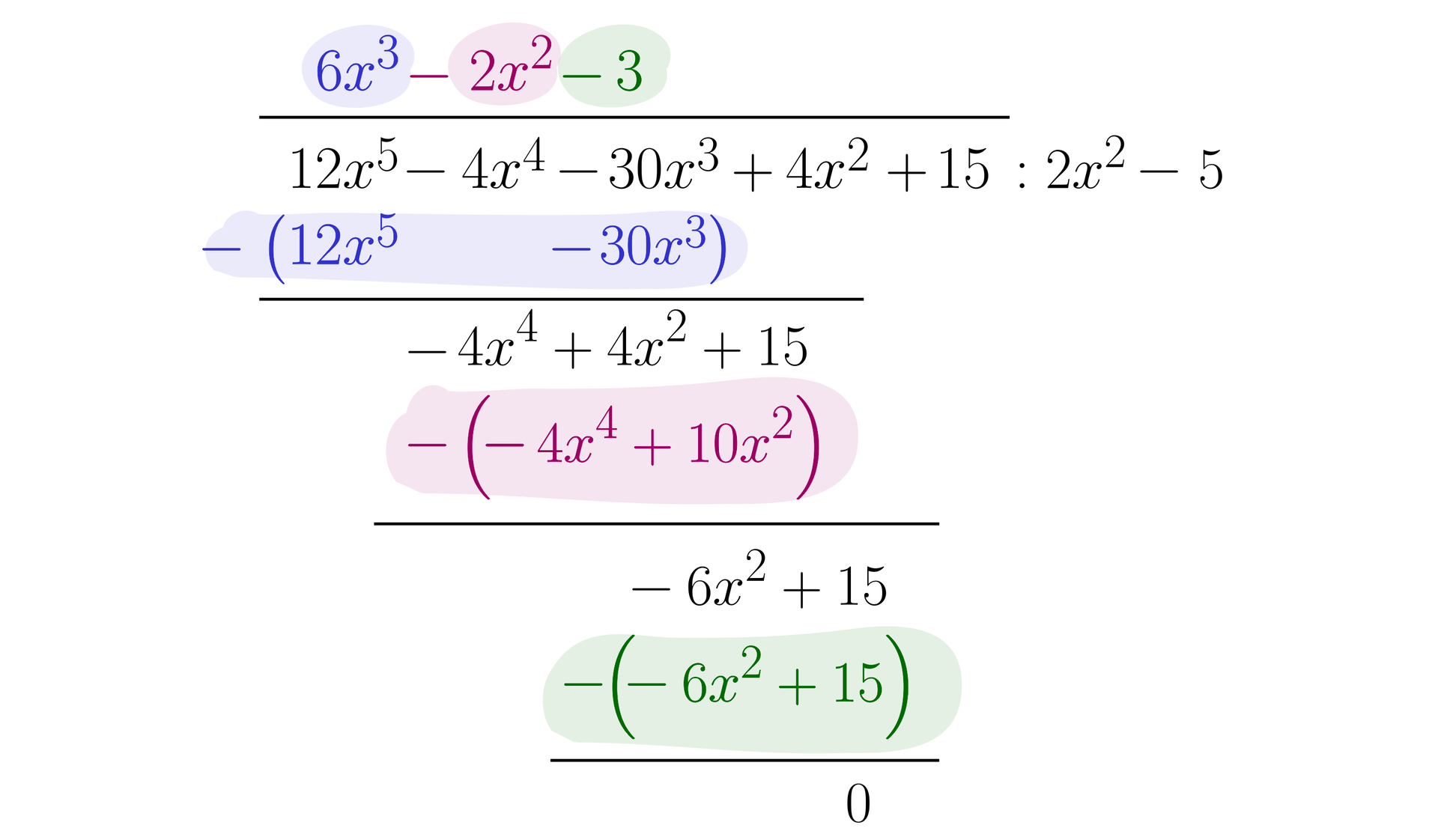
Wielomian $W\left(x\right)=12x^5-4x^4-30x^3+4x^2+15$ zapiszemy zatem w postaci:

$W\left(x\right)=\left(6x^3-2x^2-3\right)\left(2x^2-5\right)$.

• Jeżeli $W\left(x\right)$, $F\left(x\right)$ i $G\left(x\right)$ nie są wielomianami zerowymi oraz $W\left(x\right):F\left(x\right)=G\left(x\right)$, to $\text{deg}\left(G\left(x\right)\right)=\text{deg}\left(W\left(x\right)\right)-\text{deg}\left(F\left(x\right)\right)$.

• Jeżeli $W\left(x\right):F\left(x\right)=G\left(x\right)$ oraz $F\left(x\right)$ jest wielomianem zerowym, to nie możemy wykonać dzielenia.

• Jeżeli $W\left(x\right):F\left(x\right)=G\left(x\right)$ oraz $G\left(x\right)$ jest wielomianem zerowym, to $W\left(x\right)$ również jest wielomianem zerowym.

Dla każdego wielomianu $W\left(x\right)$ i niezerowego wielomianu $F\left(x\right)$ istnieją wielomiany $G\left(x\right)$ i $R\left(x\right)$ takie, że $W\left(x\right)=F\left(x\right)·G\left(x\right)+R\left(x\right)$, przy czym wielomian $R\left(x\right)$, nazywany resztą z dzielenia, jest stopnia mniejszego niż stopień wielomianu $F\left(x\right)$ lub jest wielomianem zerowym.

Wykonamy dzielenie wielomianu $W\left(x\right)=8x^3-22x^2+36x-24$ przez wielomian $F\left(x\right)=4x-5$.

Rozwiązanie

R1ThrXYyz93iX

Ilustracja przedstawia dzielenie pisemne wielomianów $8x^3-22x^2+36x-24$ oraz $4x-5$, nad działaniem znajduje się pozioma linia wyniku, pod działaniem zapisujemy wyniki dzielenia. Rozważmy pierwszy składnik dzielnej, czyli $8x^3$ i podzielmy go przez pierwszy składnik dzielnika, czyli $4x$. Wynik $2x^2$ zapisujemy nad linią wyniku nad $8x^3$, następnie mnożymy $2x^2$ razy $4x$ i wynik $8x^3$ zapisujemy z przeciwnym znakiem pod $8x^3$, dalej mnożymy $2x^2$ razy minus pięć i otrzymujemy wynik $-10x^2$, który zapisujemy z przeciwnym znakiem pod drugim składnikiem dzielnej. Kreślimy pionową linię Dokonujemy odejmowania między $8x^3$,a $8x^3$ , otrzymujemy zero, którego nie zapisujemy pod kreską, następnie dodajemy $-22x^2$ oraz $10x^2$ i dostajemy $-12x^2$, dalej przepisujemy dwa ostatnie składniki dzielnej czyli $36x-24$. Otrzymujemy $-12x^2+36x-24$, dzielimy pierwszy składnik tej sumy przez $4x$ i wynik $-3x$ zapisujemy nad linią wyniku nad $-22x^2$, następnie mnożymy $-3x$ razy $4x$ i wynik $-12x^2$ zapisujemy z przeciwnym znakiem pod $-12x^2$, dalej mnożymy $-3x$ razy minus pięć i wynik $15x$ zapisujemy z przeciwnym znakiem pod $36x$. Kreślimy pionową kreskę. Dokonujemy dodawania między $-12x^2$ , a $12x^2$, wynik zero nie zapisujemy pod kreską, dalej odejmujemy od $36x$ $15x$ i otrzymujemy $21x$, co zapisujemy pod kreską oraz przepisujemy ostatni składnik dzielnej minus dwadzieścia cztery. Otrzymujemy $21x-24$, dzielimy $21x$ przez $4x$, wynik 5 zapisujemy nad linią wyniku nad $36x$. Mnożymy pięć razy $4x$ i wynik $20x$ zapisujemy z przeciwnym znakiem pod $21x$, dalej mnożymy pięć razy minus pięć i wynik minus 25 zapisujemy pod minus 24. Kreślimy pionową kreskę. Dokonujemy odejmowania $21x$ odjąć $20x$, wynik x zapisujemy pod pionową kreską, dalej dodajemy minus 24 dodać 25 i otrzymujemy jeden co zapisujemy również pod pionową kreską. Zatem dzielenie zakończyło się z resztą równą $x+1$.

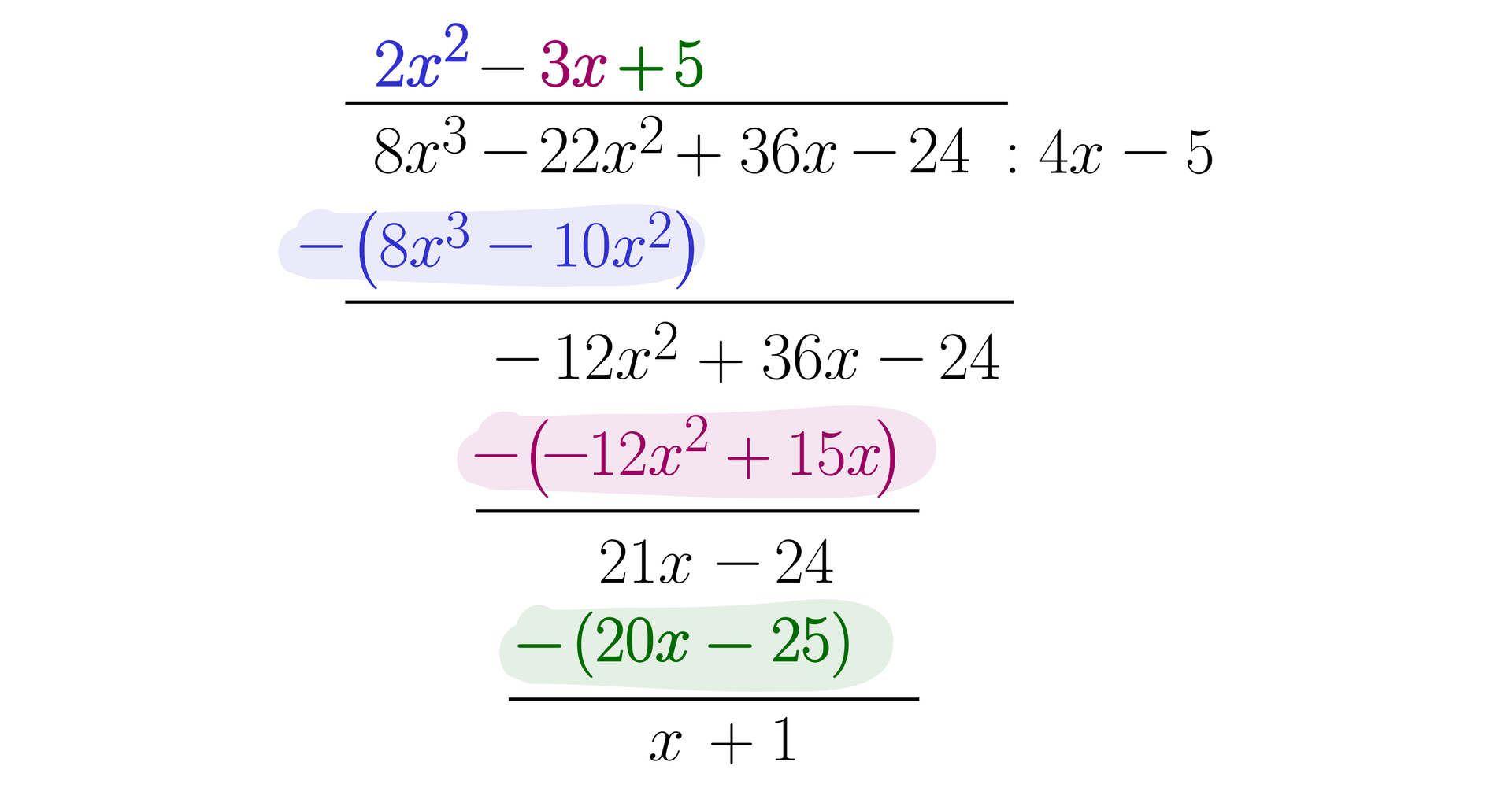
Wielomian $W\left(x\right)=8x^3-22x^2+36x-24$ zapiszemy zatem w postaci:

$W\left(x\right)=\left(2x^2-3x+5\right)\left(4x-5\right)+x+1$.

Dwumian liniowydwumian liniowyDwumian liniowy $R\left(x\right)=x+1$ jest resztą z dzielenia wielomianu $W\left(x\right)$ przez wielomian $F\left(x\right)$.

• Jeżeli $W\left(x\right)$, $F\left(x\right)$, $G\left(x\right)$ i $R\left(x\right)$ nie są wielomianami zerowymi oraz $W\left(x\right)=F\left(x\right)·G\left(x\right)+R\left(x\right)$, to $\text{deg}\left(R\left(x\right)\right)<\text{deg}\left(G\left(x\right)\right)$, jeżeli szukamy ilorazu wielomianów $W\left(x\right)$ i $F\left(x\right)$.

• Jeżeli $W\left(x\right)$, $F\left(x\right)$, $G\left(x\right)$ i $R\left(x\right)$ nie są wielomianami zerowymi oraz $W\left(x\right)=F\left(x\right)·G\left(x\right)+R\left(x\right)$, to $\text{deg}\left(R\left(x\right)\right)<\text{deg}\left(F\left(x\right)\right)$, jeżeli szukamy ilorazu wielomianów $W\left(x\right)$ i $G\left(x\right)$.

wyrażenie postaci $a{x}^k$, w którym $x$ jest zmienną rzeczywistą, $a$ jest liczbą rzeczywistą różną od zera, a wykładnik $k$ jest liczbą naturalną oznaczającą stopień jednomianu

suma dwóch jednomianów, którego stopień jest równy $1$