Przeczytaj
Rozpoczniemy od przypomnienia kilku twierdzeń.
Załóżmy, że funkcja posiada pochodną w punkcie . Jeżeli funkcja przyjmuje ekstremum lokalne w , to .
Funkcja ciągła przyjmuje ekstrema globalne.
Na mocy twierdzenia Weierstrassa otrzymujemy, że problem znalezienia najmniejszej i największej wartości funkcji ciągłej zawsze posiada rozwiązania. Warunek konieczny istnienia ekstremum lokalnego stanowi z kolei nieocenioną pomoc w poszukiwaniu tych rozwiązań. Pokażemy to na kilku prostych przykładach
Znajdziemy najmniejszą i największą wartość funkcji na przedziale oraz wszystkie argumenty, w których wartości te są przyjmowane.
Rozwiązanie
Twierdzenie Weierstrassa zapewnia, że funkcja osiąga swoje ekstrema. Jeżeli są one przyjmowane na przedziale , to pochodna funkcji musi się tam zerować na mocy warunku koniecznego dla istnienia ekstremum lokalnego.
Policzmy zatem
.
Ponieważ rozwiązaniami równania
są liczby i , więc jedynymi punktami, w których może przyjmować ekstrema są oraz .
Zauważmy dodatkowo, że do tej pory wyłączyliśmy z naszych rozważań punkty znajdujące się na brzegu przedziału, a więc punkty i . Wystarczy zatem, że porównamy wartości funkcji w punktach , , i .
Policzmy więc
, , , .
Oznacza to, że i są argumentami minimum globalnegoargumentami minimum globalnego, zaś i są argumentami maksimum globalnegoargumentami maksimum globalnego. Ponadto największą wartością jest , a najmniejszą . Na koniec przedstawimy wykres funkcji na przedziale .
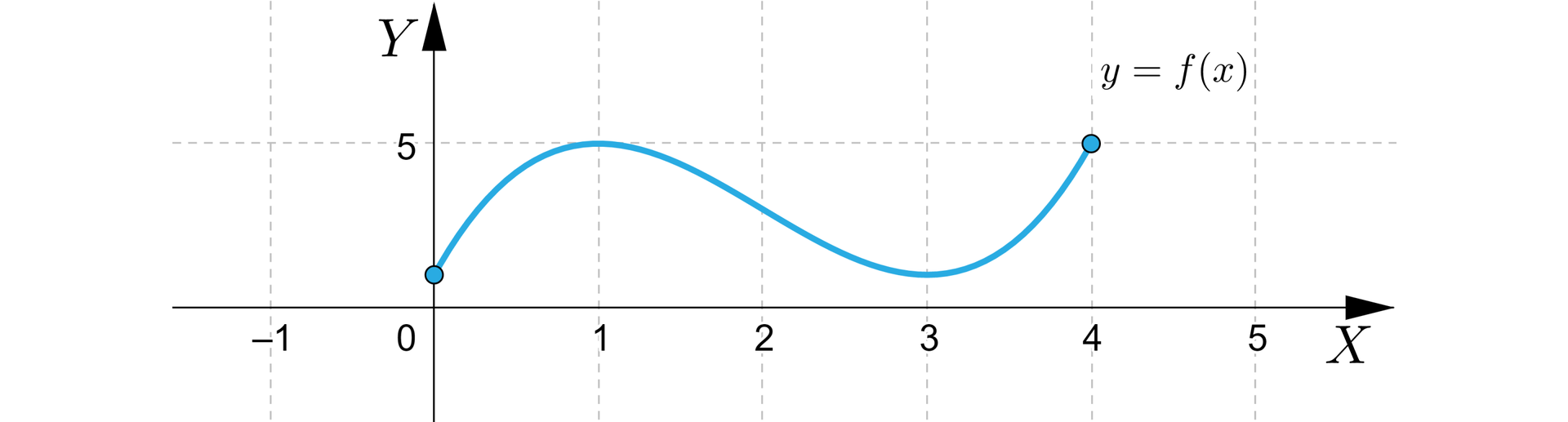
Znajdziemy ekstrema globalne funkcji na przedziale .
Rozwiązanie
Istnienie ekstremów globalnych zapewnia nam twierdzenie Weierstrassa. Rozpoczniemy od analizy na przedziale . W tym celu wyznaczymy miejsca, w których zeruje się pochodna funkcji . Mamy
lub
Funkcja nie przyjmuje zatem ekstremów na przedziale . Oznacza to, że ekstrema globalne funkcji muszą być przyjmowane w punktach oraz .
Prosty rachunek:
prowadzi nas do wniosku, że minimum globalnym funkcji na przedziale jest , zaś jej maksimum na tym samym przedziale to .
O poprawności obliczeń przekonuje nas dodatkowo wykres funkcji .

Zajmiemy się teraz poszukiwaniem ekstremów funkcji na przedziale .
Rozwiązanie
Możemy się powołać na twierdzenie Weierstrassa, by mieć pewność, że poszukiwane punkty istnieją. Aby znaleźć rozwiązania na przedziale posłużymy się ponownie warunkiem koniecznym dla istnienia ekstremum lokalnego.
Obliczając pochodną funkcji otrzymujemy
.
W celu znalezienia miejsc, w których zeruje się pochodna funkcji rozważamy równanie
.
Wykorzystamy podstawienie , , aby uprościć powyższe równanie.
Otrzymujemy:
lub .
Wracając do wyjściowej zmiennej, mamy
lub
lub
lub lub lub .
Zauważmy, że wartości oraz muszą zostać odrzucone z naszych rozważań jako punkty spoza przedziału .
Włączamy do naszej analizy (odrzucone przed chwilą) punkty na końcach przedziału i porównamy wartości funkcji w punktach , , i .
Otrzymujemy kolejno:
Ekstremami globalnymi funkcji na przedziale są więc i . Potwierdza to także wykres funkcji sporządzony poniżej

Przejdziemy do analizy funkcji „klamerkowej”, gdyż daje się ją analizować w bardzo podobny sposób.
Znajdziemy argumenty ekstremum globalnego funkcji określonej wzorem
Rozwiązanie
Łatwo zauważyć, że w każdym punkcie różnym od funkcja jest ciągła. Pokażemy, że jest ona ciągła także w punkcie . Policzmy:
,
,
.
Ponieważ funkcja jest ciągła oraz określona na przedziale domkniętym i ograniczonym możemy wykorzystać twierdzenie Weierstrassa, by przekonać się, że zadanie posiada rozwiązanie.
Znajdziemy najpierw najmniejszą i największą wartość funkcji na przedziale , a następnie poszukamy wszystkich ekstremów lokalnych funkcji na przedziale . Funkcja jest różniczkowalna na przedziale , więc aby znaleźć ekstrema lokalne na przedziale policzymy pochodną funkcji na tym przedziale i przyrównamy ją do zera.
Mamy:
.
Tym samym
, lub .
Uwzględniając wartości funkcji na końcach przedziału oraz w punktach, gdzie zeruje się pochodna funkcji otrzymujemy
Stąd największa wartość funkcji na przedziale jest przyjmowana w punkcie , zaś najmniejsza w punkcie . Podobną analizę przeprowadzimy dla przedziału . Policzmy wpierw pochodną funkcji na przedziale . Otrzymujemy:
,
a zatem
.
Funkcja nie przyjmuje zatem ekstremów w żadnym punkcie przedziału . Wystarczy więc porównać wartości
.
Najmniejsza wartość funkcji na przedziale jest przyjmowana w punkcie , zaś największa w punkcie . Ostatecznie, porównując największą wartość funkcji na przedział z jej największa wartością na przedziale otrzymujemy, że argumentem ekstremum globalnegoargumentem ekstremum globalnego funkcji na przedziale jest . Z kolei porównując najmniejsze wartości funkcji kolejno na przedziałach i jesteśmy w stanie łatwo zauważyć, że najmniejsza wartość funkcji na przedziale jest przyjmowana w . Porównajmy dodatkowo otrzymane wyniki z wykresem funkcji.
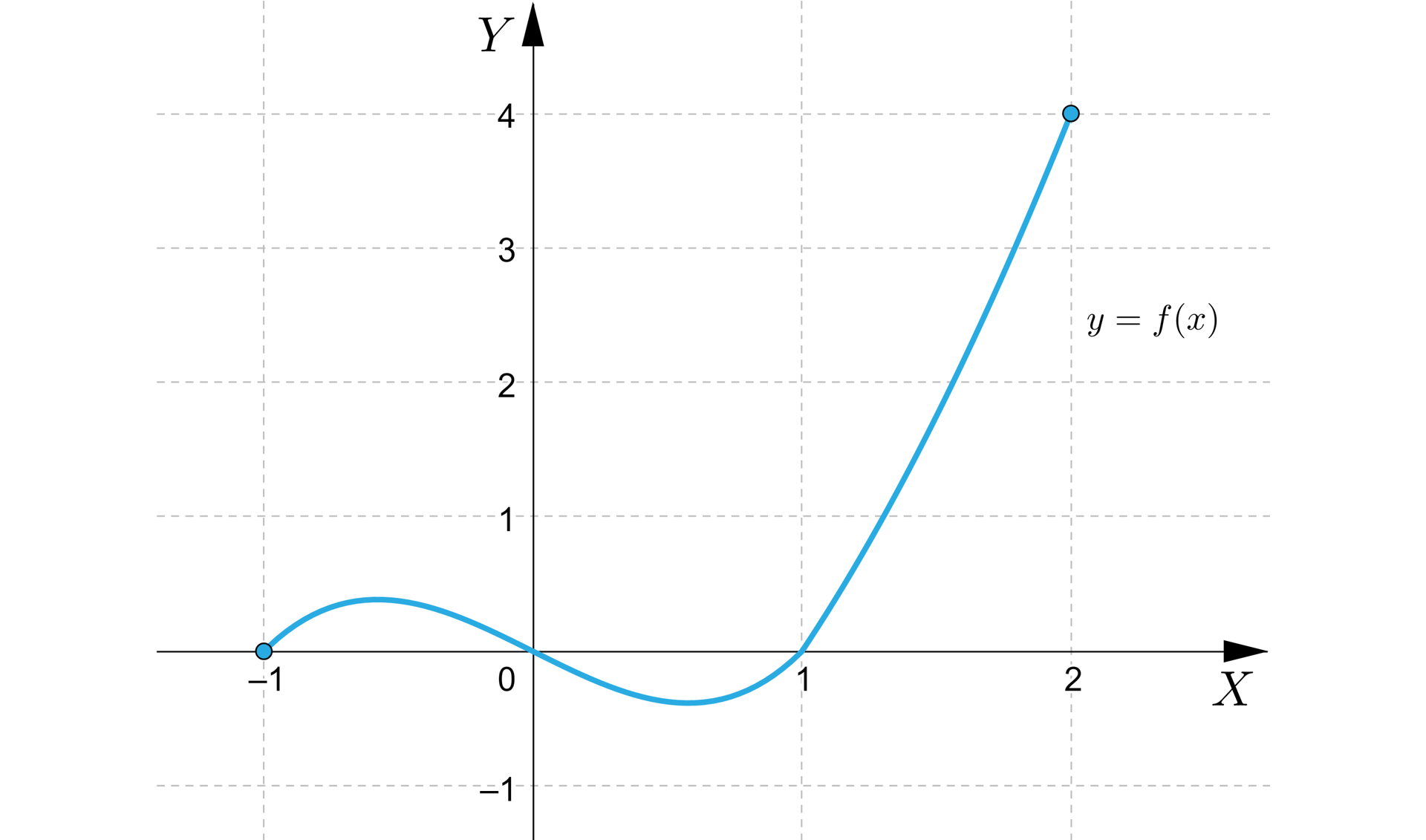
Do tej pory wykorzystywaliśmy twierdzenie Weierstrassa, aby zapewnić, że problemy, które rozważamy posiadają rozwiązania. Samo poszukiwanie rozwiązań może się jednak odbywać w podobny sposób nawet, gdy założenia twierdzenia Weierstrassa nie są spełnione.
Rozważmy funkcję określoną wzorem .
Znajdziemy jej argumenty ekstremum globalnego na przedziale , o ile te istnieją.
Rozwiązanie
Zauważmy wpierw, że funkcja nie jest określona na przedziale domkniętym. Nie możemy więc skorzystać z twierdzenia Weierstrassa. Nie mamy tym samym pewności czy największa i najmniejsza wartość funkcji istnieją. Zauważmy jednak, że funkcja jest różniczkowalna na przedziale . Oznacza to, że możemy wykorzystać warunek konieczny dla istnienia ekstremum lokalnego. Policzmy zatem:
i rozważmy równanie
Wyróżnikiem trójmianu kwadratowego jest , a zatem rozwiązaniami powyższego równania są
oraz .
Otrzymujemy zatem
.
Ponieważ funkcja określona jest na przedziale prawostronnie domkniętym, możemy dołączyć wartość z prawego końca, tj. punktu . Mamy wtedy:
.
W przypadku lewego końca musimy postępować nieco inaczej niż poprzednio. Ponieważ funkcja nie jest określona w punkcie , policzymy granicę w tym punkcie
.
Oznacza to, że funkcja nie przyjmuje największej wartości na przedziale . Tym samym jedynym punktem podejrzanym o bycie argumentem ekstremumargumentem ekstremum jest . Aby upewnić się, że ten punkt jest argumentem minimumargumentem minimum prześledzimy zmienność funkcji , badając znak jej pochodnej. Zauważmy, że wykorzystując powyższe obliczenie możemy otrzymać
.
Mianownik jest dodatni dla każdego argumentu dziedziny. Licznik zaś jest funkcją kwadratową o pierwiastkach oraz . Rysując wykres omawianego trójmianu kwadratowego zauważamy, że jest on ujemny na przedziale , zaś dodatni na przedziale . W konsekwencji pochodna jest ujemna na przedziale , a dodatnia na . Oznacza to, że funkcja maleje na przedziale , a następnie rośnie na przedziale . Możemy zatem narysować wykres funkcji , by przekonać się, że funkcja istotnie przyjmuje minimum w punkcie .
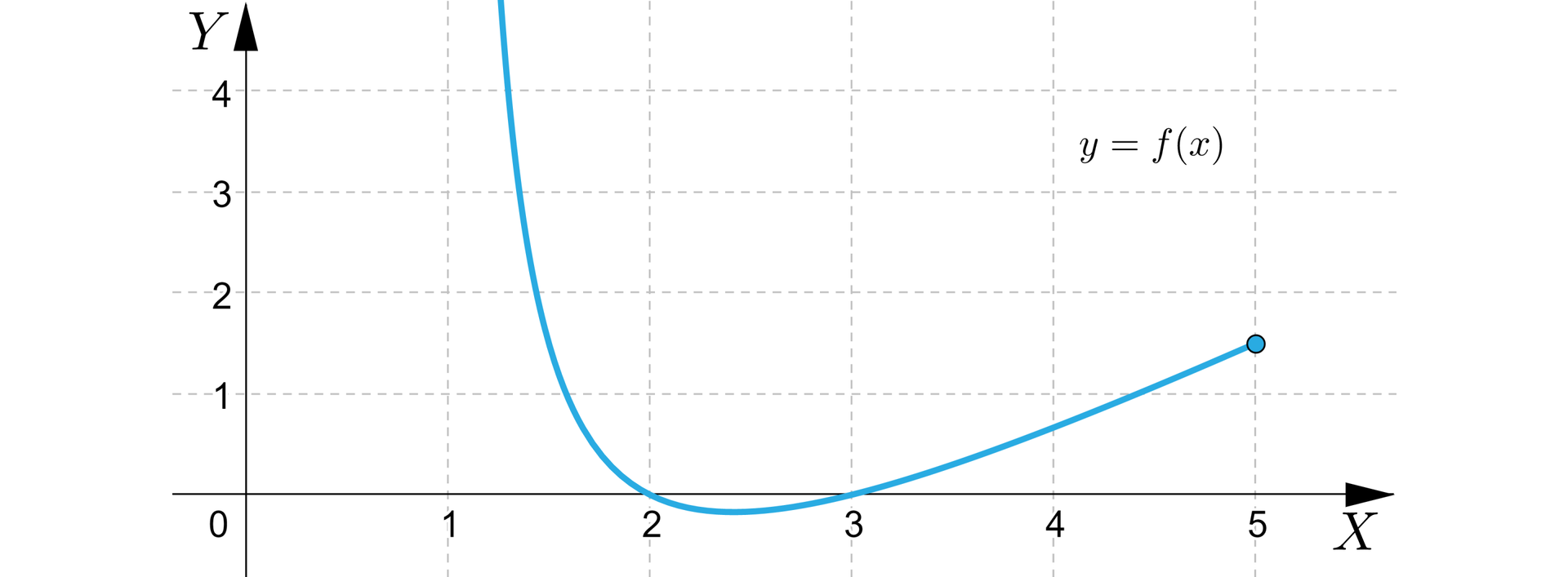
Zakończymy dość prostym przykładem, który pokazuje kolejne trudności związane z poszukiwaniem ekstremów funkcji, która nie spełnia założeń twierdzenia Weierstrassa.
Rozważmy funkcję
.
Sprawdzimy czy funkcja posiada ekstrema globalne.
Rozwiązanie
Funkcja jest różniczkowalna na przedziałach oraz . Co więcej dla oraz dla . Nie istnieje więc żadne minimum ani maksimum lokalne na przedziałach ani . Gdyby funkcja była ciągła, wystarczyłoby rozważyć punkty , i . Co więcej, jeden z tych punktów musiałby być punktem minimum funkcji na przedziale , zaś drugi punktem maksimum. Rysując wykres funkcji przekonujemy się jednak łatwo, że funkcja nie jest ciągła.
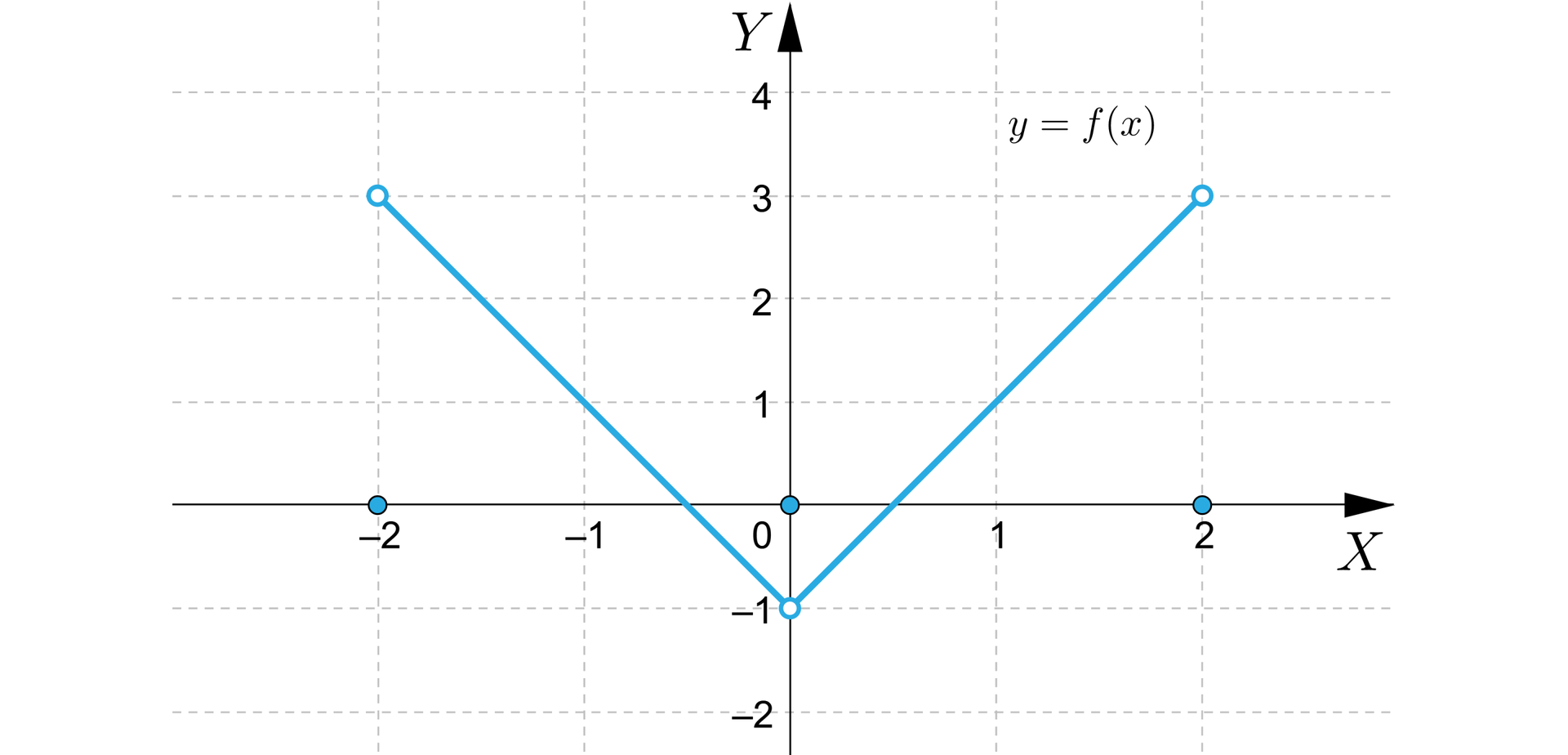
Widzimy także, że funkcja nie posiada ekstremów na przedziale .
Widzimy zatem, że badanie ekstremów funkcji jest możliwe także w sytuacji, gdy nie spełnia ona założeń twierdzenia Weierstrassa. Jest to jednak wówczas zdecydowanie bardziej skomplikowane i wymaga od nas większej uwagi.
Słownik
element dziedziny, w którym funkcja przyjmuje najmniejszą wartość
element dziedziny, w którym funkcja przyjmuje największą wartość
argument minimum lub maksimum globalnego