Przeczytaj
Obliczanie pola powierzchnipola powierzchni prostopadłościanu jest niezwykle przydatną umiejętnością w życiu codziennym. Dzięki niej możemy w łatwy sposób obliczyć na przykład, ile farby będziemy potrzebować, aby pomalować ściany pokoju oraz ile papieru prezentowego musimy kupić, aby zapakować upominki.
Pole powierzchni prostopadłościanu
Wprowadźmy następujące oznaczania:
– pole powierzchni,
– pole powierzchni bocznej,
– pole podstawy,
, , – długości krawędzi (wymiary prostopadłościanu).
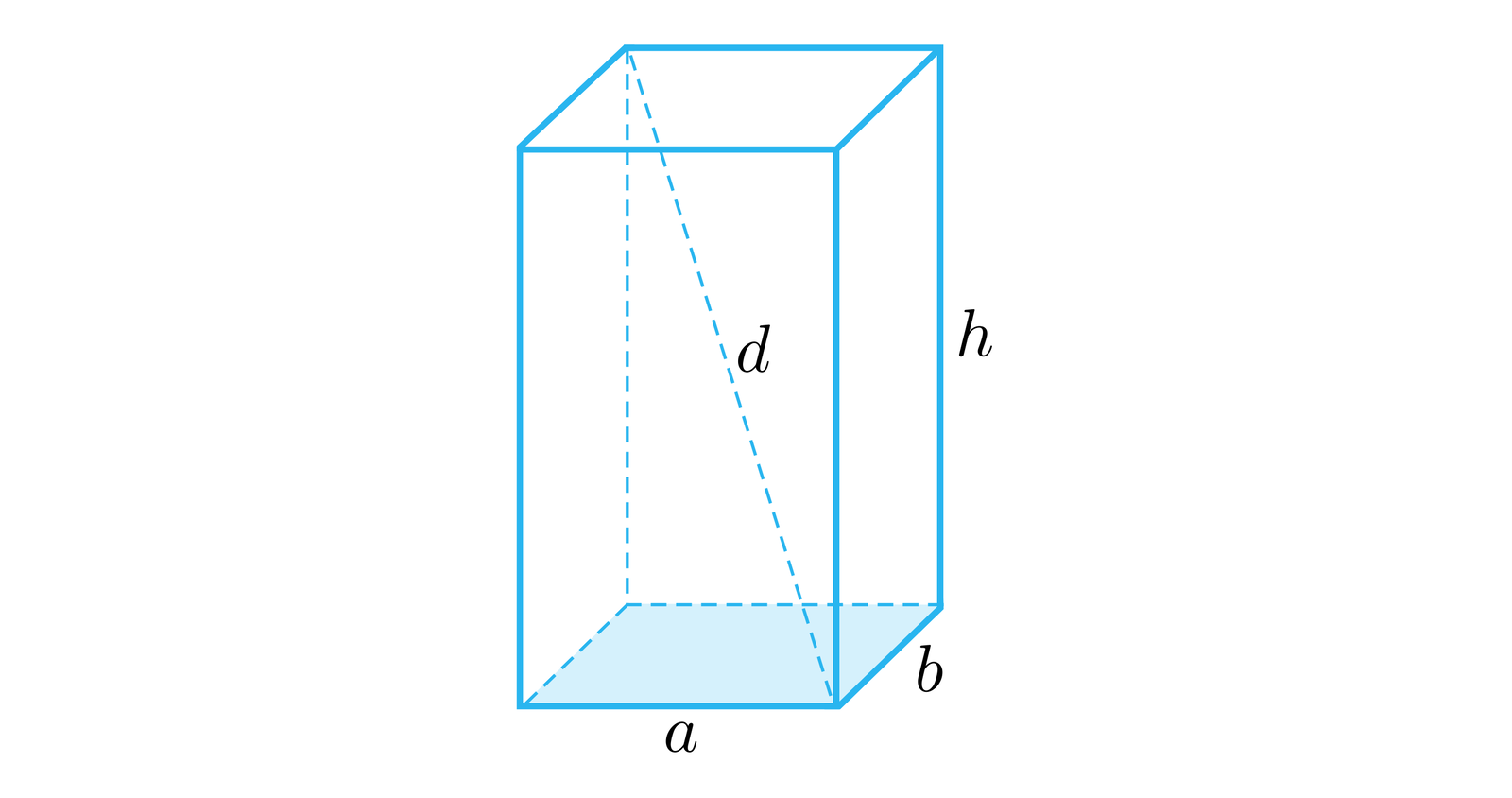
Pole powierzchni prostopadłościanuprostopadłościanu jest równe sumie pól powierzchni wszystkich jego ścian. Możemy je obliczyć wykorzystując wzór:
Wzór na pole powierzchnipole powierzchni prostopadłościanu możemy także zapisać w postaci:
Dany jest prostopadłościan, którego krawędzie podstawy są równe i , a jego wysokość wynosi . Obliczymy pole powierzchni tego prostopadłościanu.
Rozwiązanie
Dla czytelności zapisu w obliczeniach pominiemy jednostki.
Pole powierzchni prostopadłościanu obliczamy wykorzystując poznany wzór:
.
Po podstawieniu:
.
.
Pole powierzchni prostopadłościanu wynosi zatem centymetrów kwadratowych.
Pamiętajmy, że obliczanie powierzchni zawsze wiąże się z obecnością jednostek kwadratowych.
Pole powierzchni pewnego prostopadłościanu wynosi . Wysokość prostopadłościanu wynosi , a jedna z krawędzi podstawy jest równa . Obliczymy długość drugiej krawędzi podstawy prostopadłościanu.
Rozwiązanie
Oznaczmy przez długość drugiej krawędzi podstawy prostopadłościanu.
Do rozwiązania zadania wykorzystamy wzór na pole powierzchni prostopadłościanu:
.
Po podstawieniu:
.
Druga krawędź podstawy prostopadłościanu ma długość centymetry.
W prostopadłościanie o objętości stosunek długości krawędzi jest równy . Obliczymy pole powierzchni tego prostopadłościanu.
Rozwiązanie
Jeżeli stosunek długości krawędzi tego prostopadłościanu wynosi , to długości tych krawędzi można wyrazić za pomocą liczb , , .
Jeżeli objętość tego prostopadłościanu jest równa , to do wyznaczenia wartości rozwiązujemy równanie:
.
Zatem długości krawędzi tego prostopadłościanu wynoszą odpowiednio: , , .
Wobec tego pole powierzchni prostopadłościanu jest równe:
.
Obliczymy pole powierzchni prostopadłościanu z rysunku, mając daną jego wysokość , kąt nachylenia przekątnej prostopadłościanu do płaszczyzny podstawy o mierze oraz wiedząc o tym, że jedna z krawędzi podstawy prostopadłościanu jest dwa razy krótsza od przekątnej podstawy.
Rozwiązanie
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.
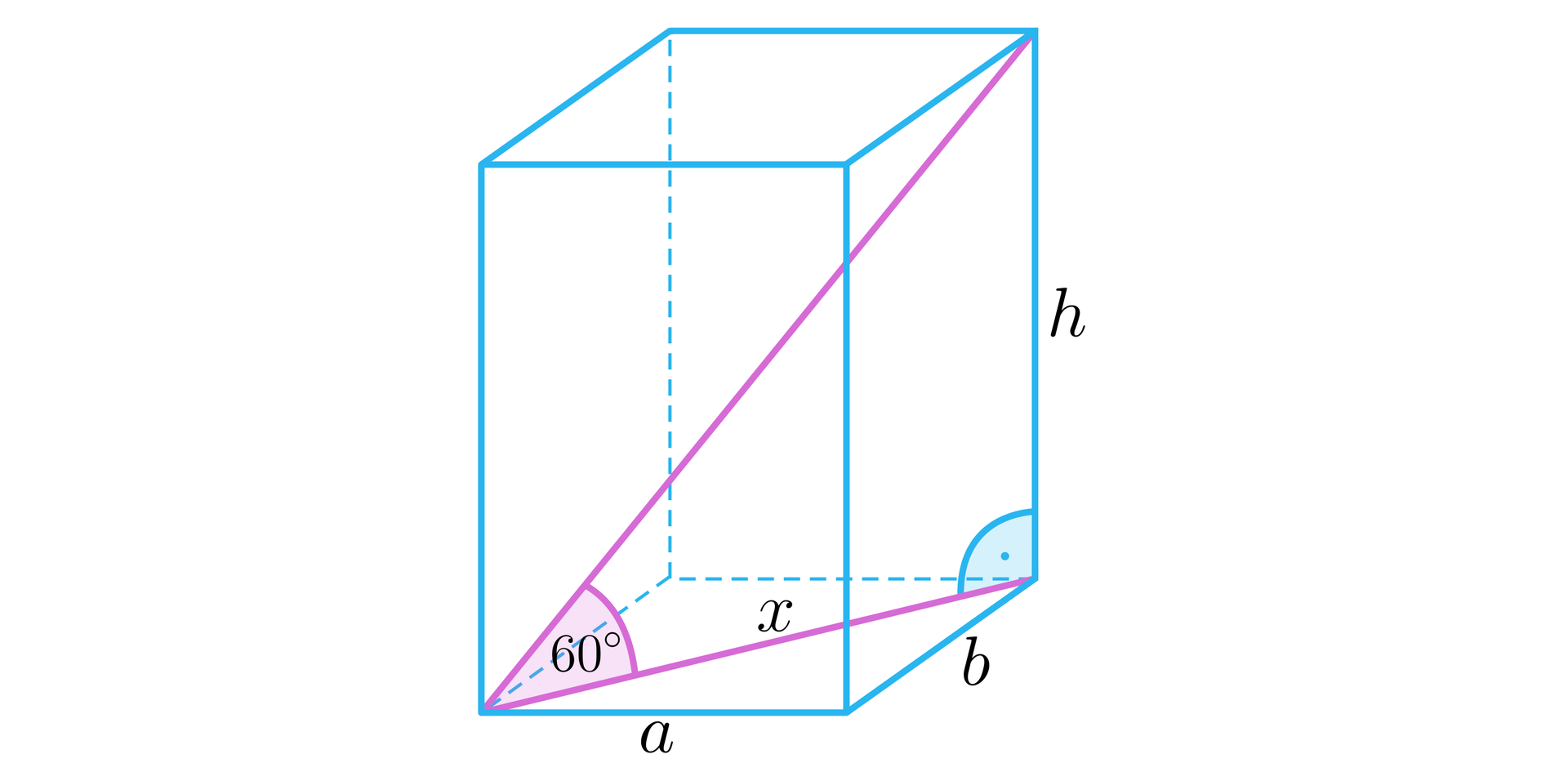
Z faktu, że kąt nachylenia przekątnej prostopadłościanu do płaszczyzny jego podstawy ma miarę otrzymujemy, że:
, czyli .
Ponieważ , zatem:
Korzystając z twierdzenia Pitagorasa, obliczamy długość krawędzi :
Wobec tego pole powierzchni prostopadłościanu jest równe:
W prostopadłościanie o podstawie kwadratowej i polu powierzchni równym , krawędź podstawy jest o jednostki krótsza od krawędzi bocznej. Obliczymy długość przekątnej tego prostopadłościanu.
Rozwiązanie
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.
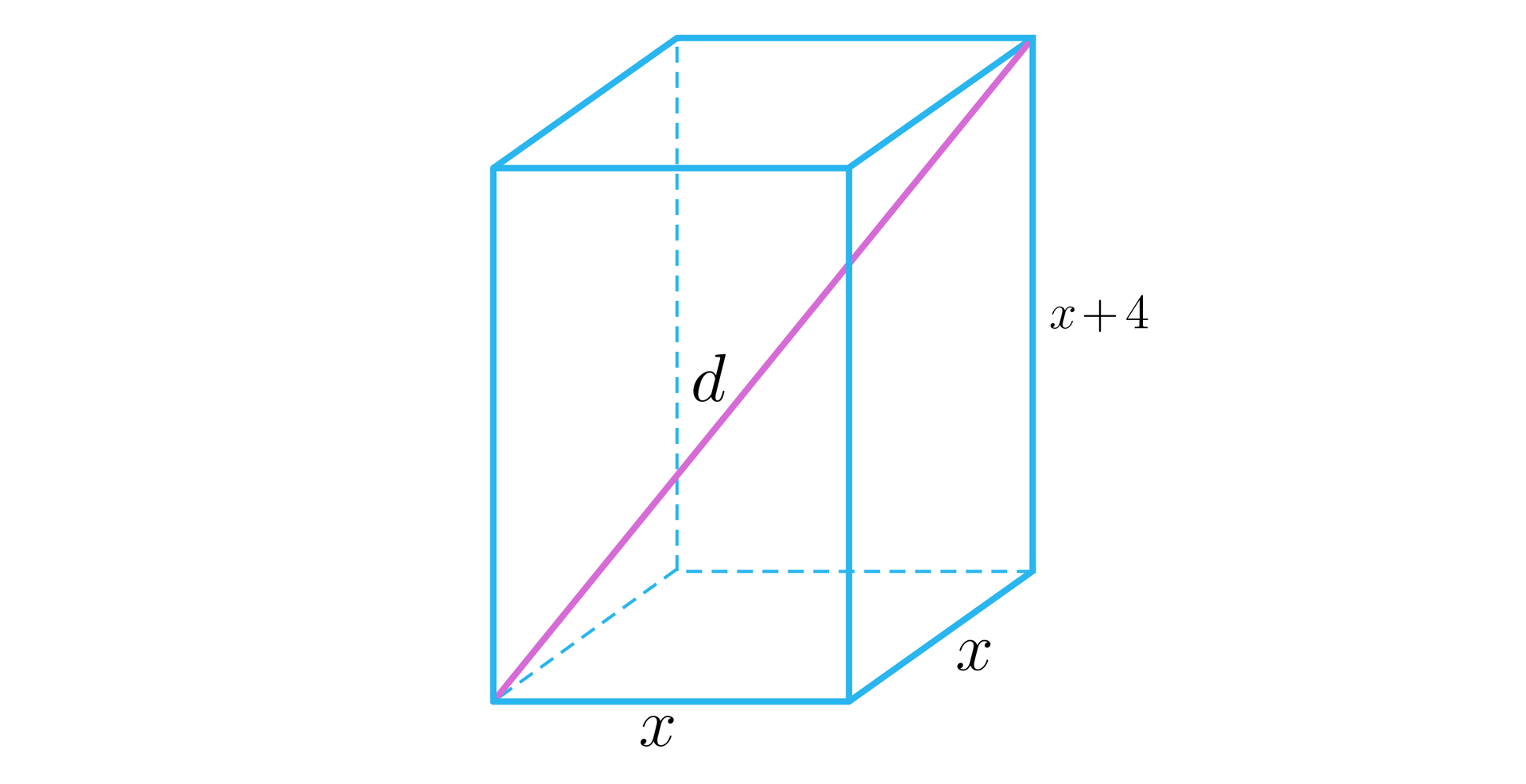
Ponieważ pole powierzchni prostopadłościanu jest równe , to do wyznaczenia wartości rozwiązujemy równanie:
.
.
Zatem krawędź podstawy prostopadłościanu ma długość , a krawędź boczna ma długość .
Wobec tego przekątna prostopadłościanu ma długość:
.
Pole powierzchni prostopadłościanu, w którym jedna z krawędzi podstawy jest trzy razy dłuższa od drugiej, jest cztery razy większe od jego pola powierzchni bocznej. Obliczymy cosinus kąta zawartego między przekątną tego prostopadłościanu, a jego krawędzią boczną.
Rozwiązanie
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.
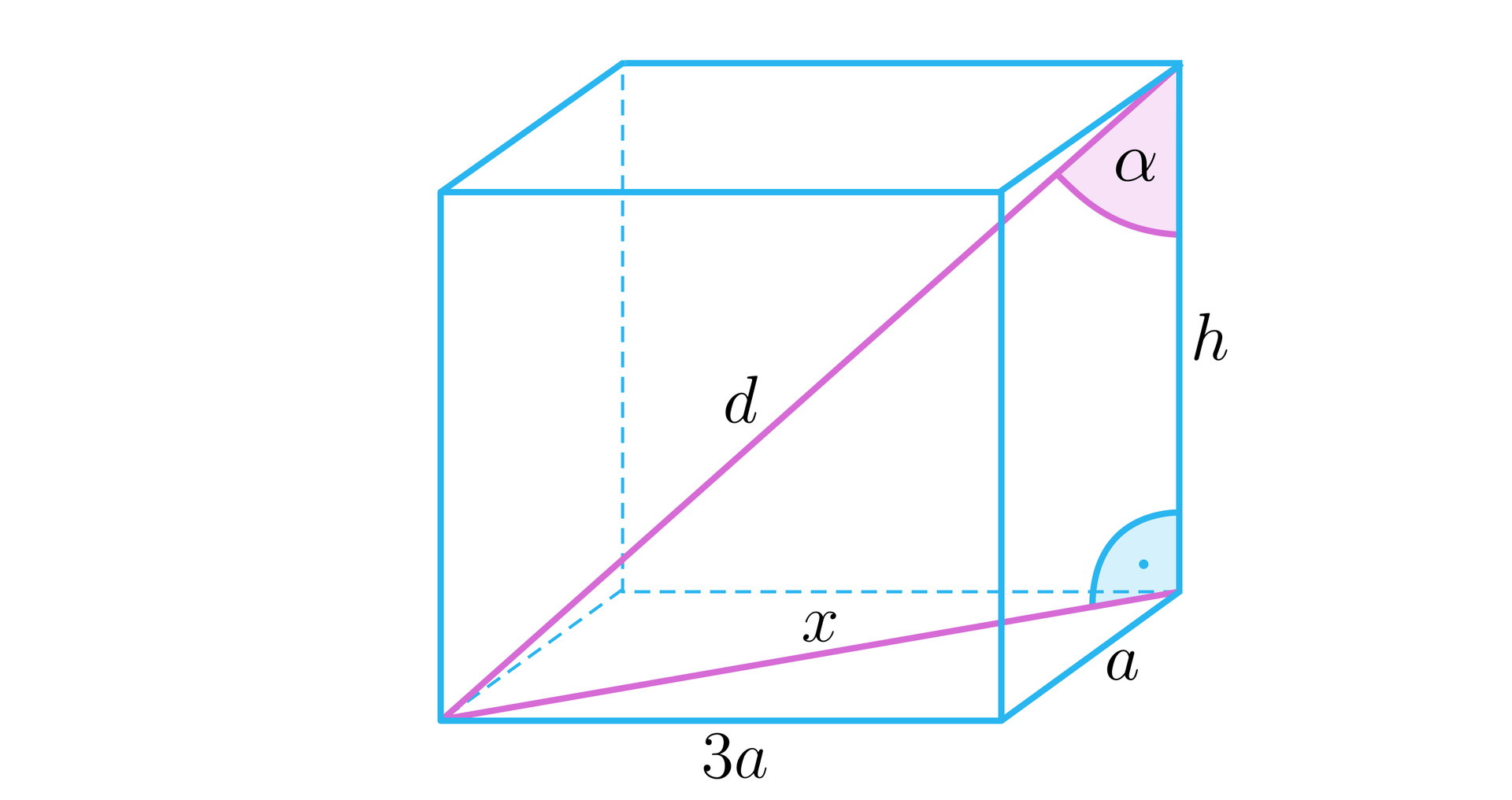
Z warunku podanego w zadaniu zachodzi zależność:
Zatem
Jeżeli wykorzystamy wzór na przekątną prostopadłościanu, to:
Cosinus kąta między przekątną prostopadłościanu, a jego krawędzią boczną jest równy:
Słownik
równoległościan, którego wszystkie ściany są prostokątami
miara, która opisuje wielkość figury geometrycznej