Przeczytaj

W materiale omówimy, jak wyznaczyć wzór funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej spełniającej określone warunki.

Wzór funkcji kwadratowej możemy zapisywać w różnych postaciach.

Postać ogólna wzoru funkcji kwadratowej:
- $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

Postać kanoniczna wzoru funkcji kwadratowej:
- $f (x) = a {(x - p)}^{2} + q$ , gdzie $p = \frac{- b}{2 a}$ oraz $q = \frac{- Δ}{4 a}$

Postać iloczynowa wzoru funkcji kwadratowej:
- $f (x) = a (x - x_{1}) (x - x_{2})$ , gdy $Δ = b^{2} - 4 a c$ , $Δ > 0$ oraz $x_{1} = \frac{- b - \sqrt{Δ}}{2 a}$ , $x_{2} = \frac{- b + \sqrt{Δ}}{2 a}$
- $f (x) = a {(x - x_{0})}^{2}$ , gdy $Δ = b^{2} - 4 a c$ , $Δ = 0$ oraz $x_{0} = \frac{- b}{2 a}$

W materiale wyznaczymy wzory funkcji kwadratowych w różnych postaciach, mając dane własności tej funkcji lub własności jej wykresu.

Wyznaczanie wzoru funkcji kwadratowej z wykorzystaniem postaci ogólnej:

mamy dane współrzędne trzech punktów (lub odczytujemy z wykresu funkcji kwadratowej), które należą do tego wykresu,

układamy i rozwiązujemy układ trzech równań liniowych z trzema niewiadomymi.

Przykład 1

Na rysunku przedstawiono parabolę, będącą wykresem funkcji kwadratowej $f$ . Wyznaczymy wzór tej funkcji $f$ w postaci ogólnej.

R1JEyuR0ATvTJ

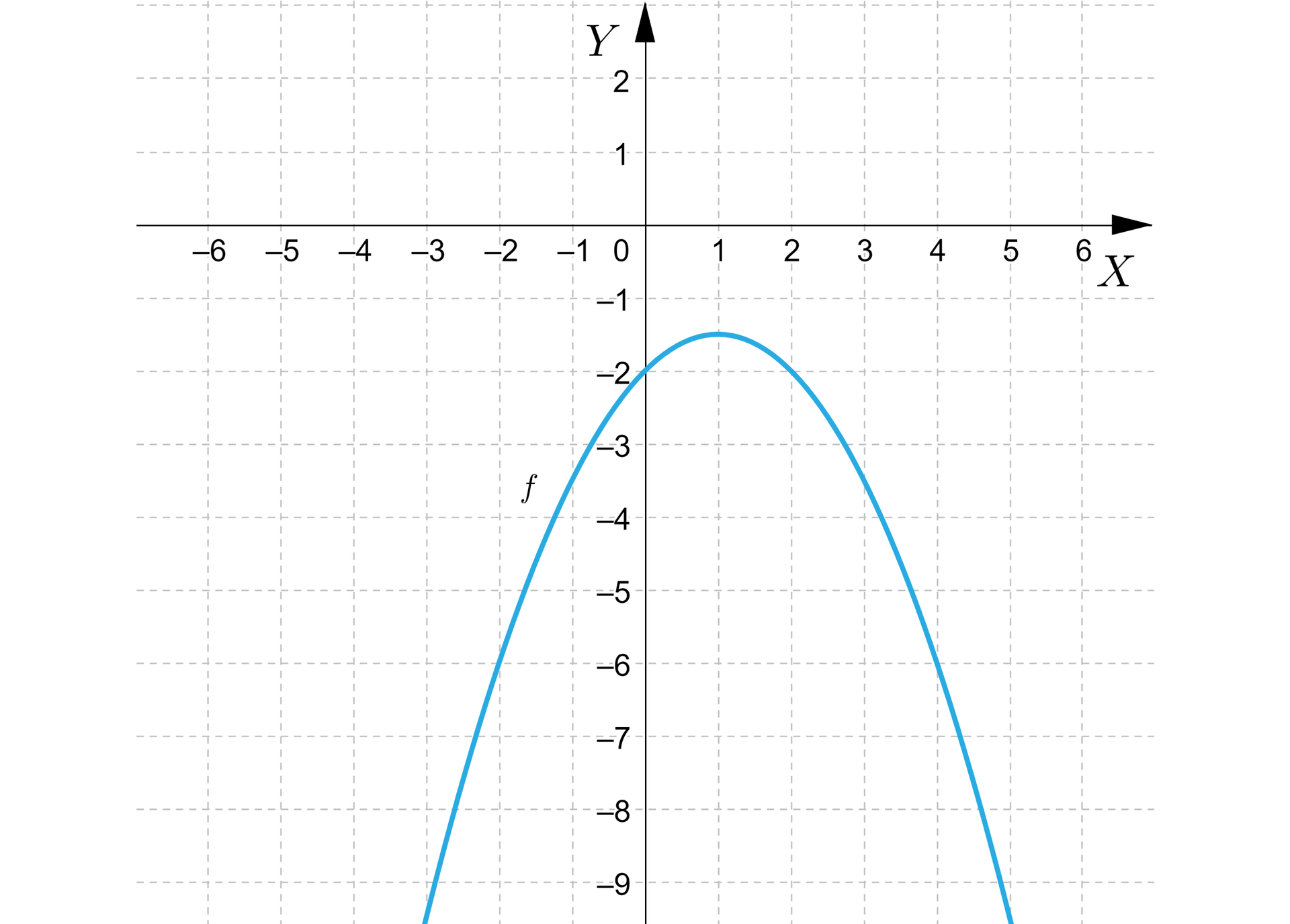
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y od minus dziewięciu do dwóch. Na płaszczyźnie narysowano parabolę o ramionach skierowanych w dół. Wierzchołek paraboli znajduje się w punkcie o współrzędnych 1;1,5. Wykres funkcji przechodzi przez punkty o współrzędnych 0;-2, 2;-2, 4;-6.

Rozwiązanie

Z wykresu funkcji $f$ odczytujemy współrzędne trzech punktów: $(0, - 2)$ , $(2, - 2)$ , $(4, - 6)$ .

Współrzędne tych punktów podstawiamy do wzoru funkcji kwadratowej $f$ w postaci ogólnej i otrzymujemy układ równań:

$\{\begin{cases} - 2 = a \cdot 0^{2} + b \cdot 0 + c \\ - 2 = a \cdot 2^{2} + b \cdot 2 + c \\ - 6 = a \cdot 4^{2} + b \cdot 4 + c \end{cases}$

Po uporządkowaniu układ równań jest postaci:

$\{\begin{cases} - 2 = c \\ - 2 = 4 a + 2 b + c \\ - 6 = 16 a + 4 b + c \end{cases}$

Ponieważ $c = - 2$ , zatem rozwiązujemy układ dwóch równań z dwiema niewiadomymi:

$\{\begin{cases} - 2 = 4 a + 2 b - 2 \\ - 6 = 16 a + 4 b - 2 \end{cases}$

Zatem $\{\begin{cases} 0 = 2 a + b \\ - 1 = 4 a + b \end{cases}$ , czyli $a = - \frac{1}{2}$ oraz $b = 1$ .

Wzór funkcji $f$ zapisujemy w postaci ogólnej:

$f (x) = - \frac{1}{2} x^{2} + x - 2$

Wyznaczanie wzoru funkcji kwadratowej z wykorzystaniem wzoru w postaci ogólnej oraz punktu przecięcia paraboli, będącej wykresem tej funkcji z osią $Y$ :

mamy dane współrzędne trzech punktów (lub odczytujemy z wykresu), które należą do paraboli, będącej wykresem funkcji kwadratowej przy założeniu, że jeden z tych punktów jest punktem przecięcia wykresu tej funkcji z osią rzędnych układu współrzędnych,

mając dany punkt przecięcia wykresu funkcji z osią rzędnych, rozwiązujemy układ równań liniowych z dwiema niewiadomymi.

Przykład 2

Wyznaczymy wzór funkcji kwadratowej $f$ w postaci ogólnej, jeżeli wiadomo, że należą do niego punkty o współrzędnych $(- 1, 1)$ , $(2, 4)$ , a parabola, będąca wykresem funkcji $f$ przecina oś $Y$ w punkcie o rzędnej $(- 4)$ .

Rozwiązanie

Jeżeli parabola, będąca wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2} + b x + c$ przecina oś $Y$ w punkcie o rzędnej $(- 4)$ , to $f (0) = - 4$ , więc $c = - 4$ .

Wzór funkcji $f$ zapisujemy w postaci: $f (x) = a x^{2} + b x - 4$ .

Jeżeli punkty o współrzędnych $(- 1, 1)$ , $(2, 4)$ należą do wykresu funkcji $f$ , to do wyznaczenia wartości $a$ i $b$ rozwiązujemy układ równań:

$\{\begin{cases} 1 = a \cdot {(- 1)}^{2} + b \cdot (- 1) - 4 \\ 4 = a \cdot 2^{2} + b \cdot 2 - 4 \end{cases}$

Po uporządkowaniu układ równań zapisujemy w postaci:

$\{\begin{cases} 1 = a - b - 4 \\ 4 = 4 a + 2 b - 4 \end{cases}$

Po rozwiązaniu układu równań otrzymujemy, że: $a = 3$ oraz $b = - 2$ .

Zatem funkcja $f$ jest określona za pomocą wzoru $f (x) = 3 x^{2} - 2 x - 4$ .

Wyznaczanie wzoru funkcji kwadratowej z wykorzystaniem wzoru w postaci iloczynowej:

mamy dane liczby (lub odczytujemy z wykresu funkcji kwadratowej), które są miejscami zerowymi funkcji kwadratowej oraz współrzędne jednego punktu, który należy do paraboli, będącej wykresem tej funkcji,

do wyznaczenia wzoru funkcji kwadratowej rozwiązujemy równanie liniowe z jedną niewiadomą.

Przykład 3

Na rysunku przedstawiono parabolę, będącą wykresem funkcji kwadratowej $f$ . Wyznaczymy wzór funkcji $f$ , korzystając ze wzoru w postaci iloczynowej.

R1OFxguI5PdeR

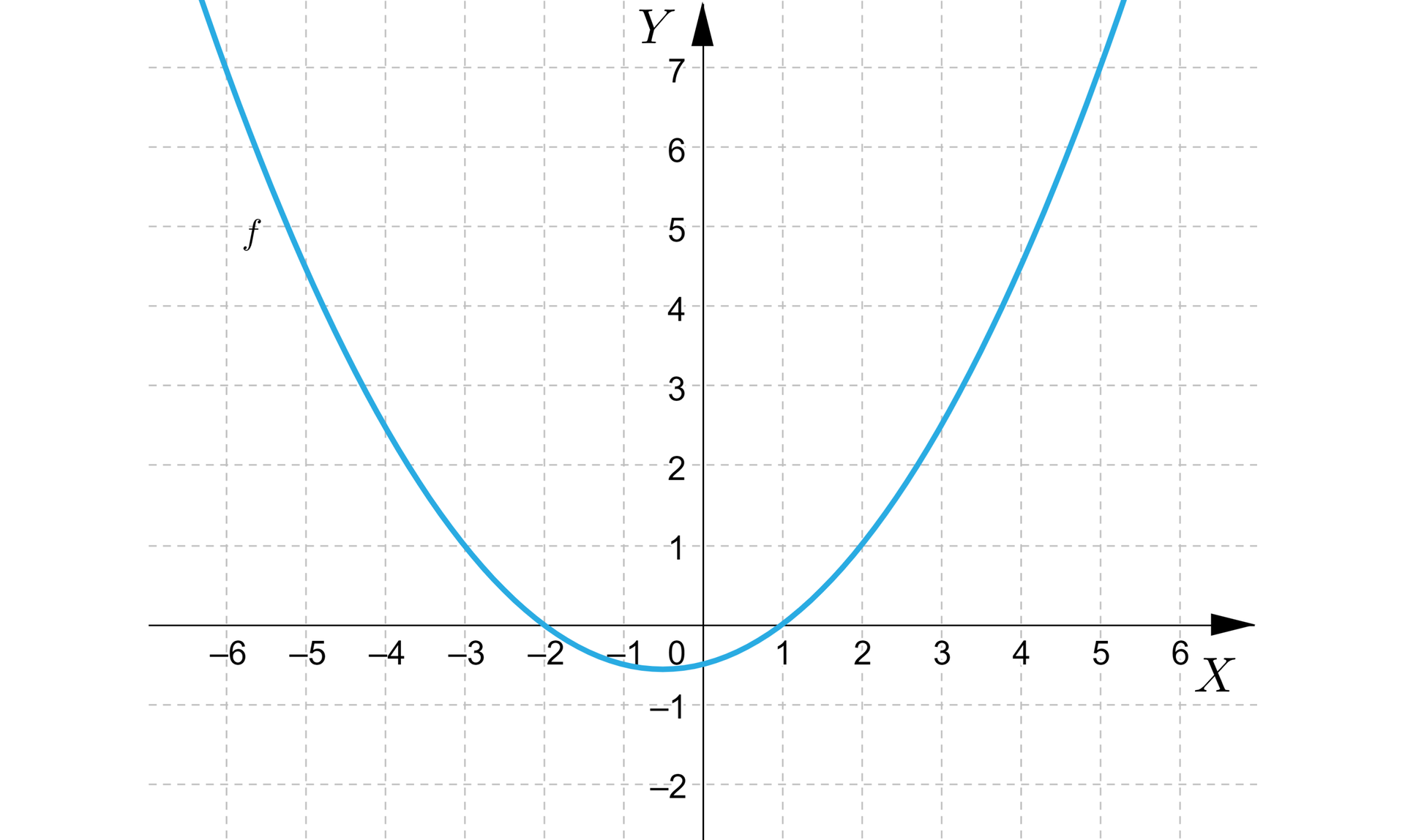
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y od minus dwóch do siedmiu. Na płaszczyźnie narysowano parabolę o ramionach skierowanych w górę. Wierzchołek paraboli znajduje się w trzeciej ćwiartce układu współrzędnych. Wykres funkcji przechodzi przez punkty o współrzędnych -3;1, 5;7.

Rozwiązanie

Z paraboli, będącej wykresem funkcji kwadratowej $f$ możemy odczytać, że miejscami zerowymi są liczby $x_{1} = - 2$ oraz $x_{2} = 1$ .

Korzystając ze wzoru funkcji kwadratowej $f$ w postaci iloczynowej mamy, że:

$f (x) = a \cdot (x + 2) (x - 1)$

Zauważmy, że do paraboli, będącej wykresem funkcji kwadratowej $f$ należy punkt o współrzędnych $(- 3, 1)$ , zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$1 = a \cdot (- 3 + 2) \cdot (- 3 - 1)$

Zatem $a = \frac{1}{4}$ .

Wobec tego funkcja $f$ jest określona za pomocą wzoru $f (x) = \frac{1}{4} (x + 2) (x - 1)$ .

Wyznaczanie wzoru funkcji kwadratowej z wykorzystaniem wzoru w postaci kanonicznej:

mamy dane (lub odczytujemy z wykresu funkcji kwadratowej) współrzędne wierzchołka paraboliparabolaparaboli, która jest wykresem tej funkcji oraz współrzędne jednego punktu, który należy do tego wykresu,

do wyznaczenia wzoru funkcji kwadratowej rozwiązujemy równanie liniowe z jedną niewiadomą.

Przykład 4

Wiadomo, że wierzchołkiem paraboliparabolaparaboli, będącej wykresem funkcji kwadratowej $f$ jest punkt o współrzędnych $(- 2, - 5)$ oraz do tego wykresu należy punkt o współrzędnych $(- 1, 1)$ . Wyznaczymy wzór funkcji $f$ w postaci kanonicznej.

Rozwiązanie

Jeżeli wiadomo, że wierzchołkiem paraboli, będącej wykresem funkcji kwadratowej $f$ jest punkt o współrzędnych $(- 2, - 5)$ , to wzór funkcji kwadratowej $f$ zapisujemy w postaci:

$f (x) = a \cdot {(x + 2)}^{2} - 5$

Jeżeli do paraboli, będącej wykresem funkcji $f$ należy punkt o współrzędnych $(- 1, 1)$ , to do wyznaczenia wartości $a$ rozwiązujemy równanie:

$1 = a \cdot {(- 1 + 2)}^{2} - 5$

Zatem $a = 6$ , więc wzór funkcji kwadratowej $f$ zapisujemy w postaci kanonicznej $f (x) = 6 \cdot {(x + 2)}^{2} - 5$ .

Wzory funkcji kwadratowychfunkcja kwadratowafunkcji kwadratowych możemy znajdować również wtedy, gdy podane są własności funkcji kwadratowej lub jej wykresu takie, jak: wartość najmniejsza lub największa, czy oś symetrii paraboli.

Przykład 5

Dana jest funkcja kwadratowa $f$ określona wzorem $f (x) = - x^{2} + b x + c$ . Wyznaczymy wartości współczynników $b$ i $c$ we wzorze tej funkcji, jeżeli jej miejscami zerowymi są liczby $(- 2)$ oraz $4$ .

Rozwiązanie

Ponieważ dane są miejsca zerowe funkcji $f$ , więc wykorzystamy postać iloczynową wzoru funkcji kwadratowej.

Zatem $f (x) = - (x + 2) (x - 4)$ .

Po przekształceniu tego wzoru do wzoru w postaci ogólnej mamy:

$f (x) = - (x + 2) (x - 4) = - (x^{2} - 4 x + 2 x - 8) = - x^{2} + 2 x + 8$

Wobec tego $b = 2$ i $c = 8$ .

Przykład 6

Wiadomo, że osią symetrii paraboli, będącej wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = 2 x^{2} + b x - 3$ jest prosta o równaniu $x = - 3$ . Wyznaczymy wartość współczynnika $b$ .

Rozwiązanie

Ponieważ prosta o równaniu $x = - 3$ jest osią symetrii paraboli, będącej wykresem funkcji $f$ , zatem $p = - 3$ .

Jeżeli skorzystamy ze wzoru $p = \frac{- b}{2 a}$ , to $- 3 = \frac{- b}{2 \cdot 2}$ .

Zatem $b = 12$ .

Przykład 7

Wyznaczymy wzór funkcji kwadratowej $f$ określonej wzorem $f (x) = - 3 x^{2} + b x + c$ , jeżeli wierzchołkiem jej wykresu jest punkt o współrzędnych $(1, - 5)$ .

Rozwiązanie

Wykorzystamy wzory $p = \frac{- b}{2 a}$ oraz $q = \frac{- Δ}{4 a}$ .

Obliczamy $∆$ :

$Δ = b^{2} - 4 \cdot (- 3) \cdot c = b^{2} + 12 c$

Zatem $p = \frac{- b}{2 \cdot (- 3)} = \frac{b}{6}$ oraz $q = \frac{- b^{2} - 12 c}{4 \cdot (- 3)} = \frac{- b^{2} - 12 c}{- 12}$ .

Do wyznaczenia wartości współczynników $b$ i $c$ rozwiązujemy układ równań:

$\{\begin{cases} 1 = \frac{b}{6} \\ - 5 = \frac{- b^{2} - 12 c}{- 12} \end{cases}$

Wobec tego $b = 6$ oraz $c = - 8$ .

Wzór funkcji kwadratowej $f$ zapisujemy w postaci ogólnej $f (x) = - 3 x^{2} + 6 x - 8$ .

Przykład 8

Wyznaczymy wartości parametru $m$ , dla których prosta o równaniu $y = - m$ nie ma punktów wspólnych z parabolą, która jest wykresem funkcji określonej wzorem $f (x) = 2 x^{2} - 4 x + m$ .

Rozwiązanie:

W celu wyznaczenia punktów wspólnych prostej i paraboli rozwiązujemy układ równań:

$\{\begin{cases} y = - m \\ y = 2 x^{2} - 4 x + m \end{cases}$

Zatem:

$- m = 2 x^{2} - 4 x + m$

Równanie przekształcamy do postaci:

$2 x^{2} - 4 x + 2 m = 0$

Parabola oraz prosta nie będą miały punktów wspólnych, gdy wyróżnik trójmianu jest mniejszy od $0$ .

Wobec tego

$∆ = {(- 4)}^{2} - 4 \cdot 2 \cdot 2 m = 16 - 16 m$

$16 - 16 m < 0$

$m > 1 \Rightarrow m \in (1, \infty)$

Zatem prosta i parabola nie mają punktów wspólnych, gdy $m \in (1, \infty)$ .

Przykład 9

Wyznaczymy wzór funkcji kwadratowej $f$ w postaci ogólnej, jeżeli wiadomo, że suma miejsc zerowych tej funkcji wynosi $(- 1)$ , iloczyn $(- 2)$ , a do paraboli, będącej wykresem tej funkcji należy punkt o współrzędnych $(2, 16)$ .

Rozwiązanie:

Zauważmy, że jeśli $x_{1}$ i $x_{2}$ są miejscami zerowymi funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2} + b x + c$ , to:

$x_{1} + x_{2} = \frac{- b - \sqrt{∆}}{2 a} + \frac{- b + \sqrt{∆}}{2 a} = \frac{- b}{a}$

$x_{1} \cdot x_{2} = \frac{- b - \sqrt{∆}}{2 a} \cdot \frac{- b + \sqrt{∆}}{2 a} = \frac{c}{a}$

Z danych zadania wynika, że $x_{1} + x_{2} = - 1$ , $x_{1} \cdot x_{2} = - 2$ oraz $f (2) = 16$ .

Zatem:

$- 1 = \frac{- b}{a}$ , czyli $b = a$

$- 2 = \frac{c}{a}$ , czyli $c = - 2 a$

Wobec tego wzór funkcji $f$ zapisujemy w postaci:

$f (x) = a x^{2} + a x - 2 a$

Ponieważ $f (2) = 16$ , to do wyznaczenia wartości $a$ rozwiązujemy równanie:

$16 = a \cdot 2^{2} + a \cdot 2 - 2 a$

Czyli $a = 4$ , $b = 4$ , $c = - 8$ .

Zatem funkcja $f$ jest określona wzorem $f (x) = 4 x^{2} + 4 x - 8$ .

Zauważmy jeszcze, że wyróżnik trójmianu kwadratowego jest dodatni (co jest warunkiem tego, aby uzyskana funkcja kwadratowa miała dwa miejsca zerowe).

Słownik

funkcja kwadratowa

funkcja określona na zbiorze $ℝ$ wzorem

f (x) = a x^{2} + b x + c

gdzie $a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

parabola

wykres funkcji kwadratowej

Wprowadzenie

Infografika

Słownik