Przeczytaj

Okrąg na płaszczyźnie kartezjańskiej opisujemy za pomocą równania. Wyróżniamy dwie postacie tego równania:

równanie okręgu w postaci ogólnej $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , gdzie promień okręgu obliczamy ze wzoru $r = \sqrt{a^{2} + b^{2} - c}$ , zaś punkt $S = (a, b)$ jest środkiem okręgu,
równanie okręgu w postaci kanonicznej ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , gdzie $r$ nazywamy promieniem okręgu, zaś punkt $S = (a, b)$ środkiem okręgu.

Prostą na płaszczyźnie opisujemy za pomocą równania. Wyróżniamy dwie postacie tego równania:

postać ogólną prostej $A x + B y + C = 0$ , gdzie $A, B, C \in ℝ$ oraz $A$ i $B$ nie są jednocześnie równe $0$ ,
postać kierunkową prostej $y = a x + b$ , gdzie $a, b \in ℝ$ .

Do badania wzajemnego położenia prostej i okręgu wykorzystamy wzór na odległość $d$ punktu $S = (a, b)$ od prostej $k$ danej wzorem $A x + B y + C = 0$ .

Wzór ten przedstawia się następująco:

$d (S, k) = \frac{|A \cdot a + B \cdot b + C|}{\sqrt{A^{2} + B^{2}}}$ .

Liczba punktów wspólnych prostej i okręgu na płaszczyźnie kartezjańskiej zależy od odległości prostej od środka okręgu.

Prosta i okrąg na płaszczyźnie kartezjańskiej:

przecinają się w dwóch punktach $A$ i $B$ , gdy zachodzi warunek: $d (S, k) < r$ ,

R1Gmpu7dpSrrm

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na płaszczyźnie narysowano okrąg o środku w punkcie S oraz ukośną prostą k przecinającą okrąg w punktach A i B. Ze środka poprowadzono do prostej odległość d do punktu P leżącego na tej prostej. Oczywiście punkt P leży w części prostej biegnącej wewnątrz okręgu pomiędzy punktami A i B.

Zauważmy, że $d (S, k) = |S P|$ .

Prostą $k$ nazywamy sieczną.

przecinają się w jednym punkcie $P$ , gdy zachodzi warunek: $d (S, k) = r$ ,

R1FuNdR7UsoJM

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na płaszczyźnie narysowano okrąg o środku w punkcie S i prostą k styczną do okręgu w punkcie S. Poprowadzono odległość d od środka S do punktu styczności P. Odległość ta jest równa promieniowi r okręgu.

Zauważmy, że $r = |S P|$ .

Mówimy, że okrąg i prosta są styczne, a prosta $k$ jest styczną do okręgu.

nie przecinają się, gdy zachodzi warunek: $d (S, k) > r$ .

R14ZJqNagixUG

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na płaszczyźnie narysowano okrąg o środku S oraz ukośną prostą k rozłączną z okręgiem. Z punktu S poprowadzono odległość d do punktu P należącego do prostej. Odległość d wykracza poza obszar okręgu.

Ważne!

Okrąg i prosta przecinają się co najwyżej w dwóch punktach.

Przykład 1

Zbadamy wzajemne położenie prostej o równaniu $2 x - 3 y + 5 = 0$ i okręgu o równaniu ${(x - 1)}^{2} + y^{2} = 9$ .

Rozwiązanie:

Z równania okręgurównanie okręgurównania okręgu możemy odczytać, że $S = (1, 0)$ oraz $r = 3$ .

Obliczymy odległość punktu $S$ od podanej prostej.

Zatem:

$d = \frac{|2 \cdot 1 - 3 \cdot 0 + 5|}{\sqrt{2^{2} + {(- 3)}^{2}}} = \frac{7}{\sqrt{13}} = \frac{7 \sqrt{13}}{13}$ .

Zauważmy, że $d = \frac{7 \sqrt{13}}{13} < 3 = r$ , zatem prosta i okrąg przecinają się w dwóch punktach.

Jeżeli równanie prostejrównanie prostejrównanie prostej zapisane jest w postaci kierunkowej, to przekształcamy je najpierw do postaci ogólnej, a następnie wyznaczamy odległość środka okręgu od tej prostej.

Przykład 2

Zbadamy wzajemne położenie prostej o równaniu $y = \frac{1}{2} x - 3$ i okręgu o równaniu $x^{2} + {(y - 2)}^{2} = 16$ .

Rozwiązanie:

Z równania okręgu możemy odczytać, że $S = (0, 2)$ oraz $r = 4$ .

Zapiszemy równanie prostej $y = \frac{1}{2} x - 3$ w postaci ogólnej.

Po przekształceniu mamy: $x - 2 y - 6 = 0$ .

Obliczymy odległość punktu $S$ od podanej prostej.

Zatem:

$d = \frac{|1 \cdot 0 - 2 \cdot 2 - 6|}{\sqrt{1^{2} + {(- 2)}^{2}}} = \frac{10}{\sqrt{5}} = 2 \sqrt{5}$ .

Zauważmy, że $d = 2 \sqrt{5} > 4 = r$ , zatem prosta i okrąg nie mają punktów wspólnych.

Czasami równanie okręgu jest zapisane w postaci ogólnej. Nie odczytamy wówczas bezpośrednio współrzędnych środka i długości promienia, ale obliczamy je ze wzorów.

Przykład 3

Określimy wzajemne położenie prostej o równaniu $2 x - y - 1 = 0$ i okręgu o równaniu $x^{2} + 4 x + y^{2} = 0$ .

Rozwiązanie:

Korzystając ze wzoru na równanie okręgu w postaci ogólnej $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , obliczamy wartości współczynników $a$ , $b$ oraz $c$ .

Zatem: $- 2 a = 4$ , $- 2 b = 0$ oraz $c = 0$ .

Czyli $a = - 2$ , $b = 0, c = 0$ .

Środek okręgu $S = (- 2, 0)$ .

Obliczamy długość promienia okręgu $r = \sqrt{{(- 2)}^{2} + 0^{2} - 0} = 2$ .

Wyznaczamy odległość środka $S$ okręgu od podanej prostej.

$d = \frac{|2 \cdot (- 2) - 1 \cdot 0 - 1|}{\sqrt{2^{2} + {(- 1)}^{2}}} = \sqrt{5}$ .

Ponieważ $d = \sqrt{5} > 2 = r$ , zatem prosta i okrąg nie mają punktów wspólnych.

W łatwy sposób można określić wzajemne położenie okręgu i prostej, która jest równoległa lub prostopadła do osi układu współrzędnych.

Przykład 4

Zbadamy wzajemne położenie prostej o równaniu $y = m$ , gdzie $m \in ℝ$ i okręgu o równaniu ${(x - 1)}^{2} + y^{2} = 4$ .

Rozwiązanie:

Z równania okręgu możemy odczytać, że $S = (1, 0)$ oraz $r = 2$ .

Przedstawmy na rysunku wzajemne położenie tego okręgu z prostą o równaniu $y = 2$ .

RIhlNcBkg4AFo

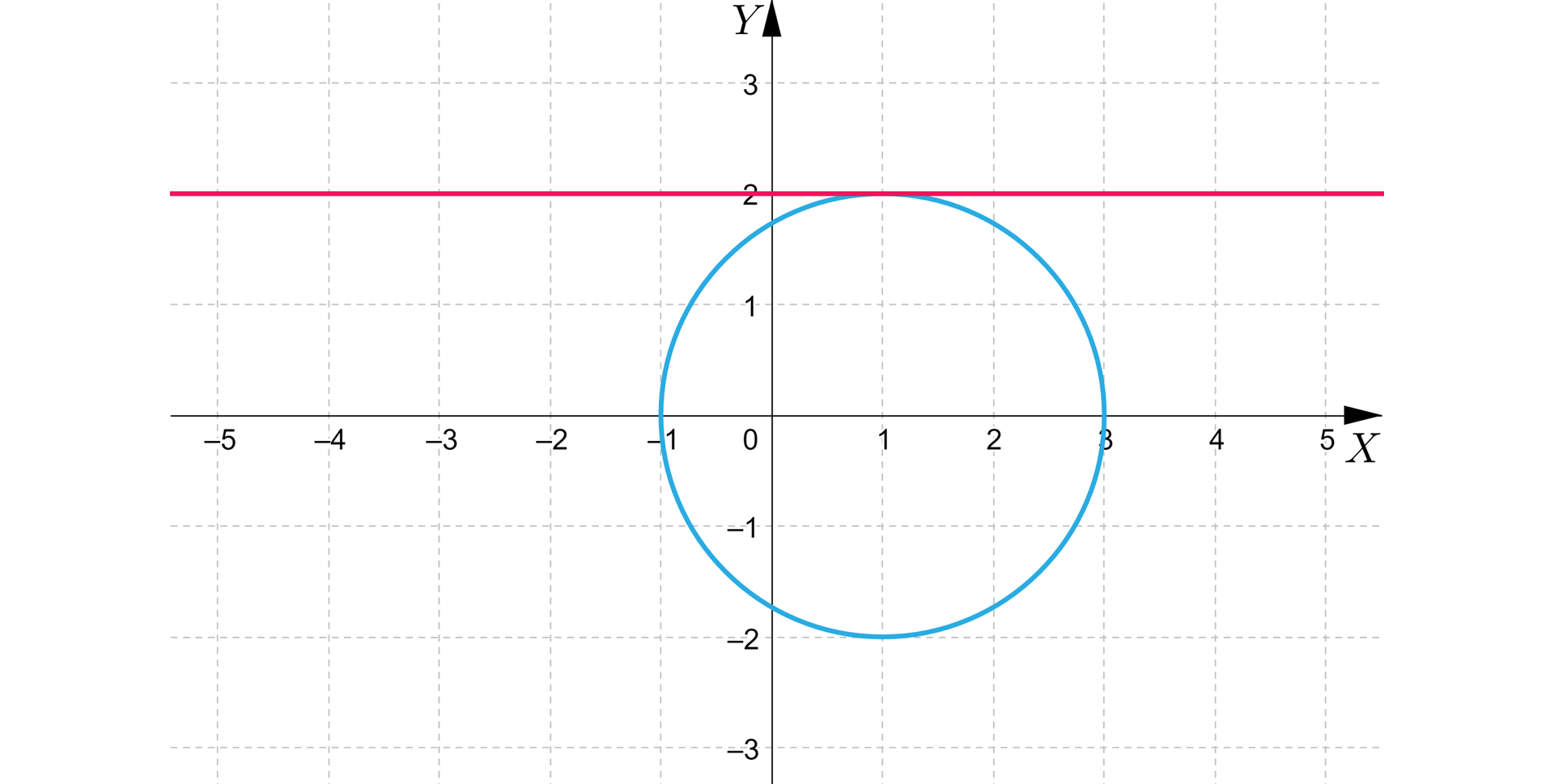
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie wykreślono okrąg o środku w punkcie nawias 1 przecinek 0 zamknięcie nawiasu i o promieniu o długości dwa. Nad okręgiem narysowano poziomą styczną do okręgu. Punkt styczności ma współrzędne nawias 1 przecinek 2 zamknięcie nawiasu.

Możemy zauważyć, że dla różnych wartości parametru $m$ , gdzie $m \in ℝ$ , prosta i okrąg mają:

$0$ punktów wspólnych, gdy $m \in (- \infty, - 2) \cup (2, \infty)$ ,
$1$ punkt wspólny, gdy $m \in \{- 2, 2\}$ ,
$2$ punkty wspólne, gdy $m \in (- 2, 2)$ .

W celu wyznaczenia punktów wspólnych prostej i okręgu możemy rozwiązać układ równań, w którym jedno równanie jest liniowe, a drugie kwadratowe. Na podstawie rozwiązania możemy stwierdzić, jakie jest ich wzajemne położenie.

Przykład 5

Wyznaczymy punkty wspólne prostej o równaniu $y = - x + 4$ i okręgu o równaniu ${(x - 1)}^{2} + y^{2} = 4$ .

Rozwiązanie:

W celu wyznaczenia punktów wspólnych rozwiążemy układ równań:

$\{\begin{cases} y = - x + 4 \\ {(x - 1)}^{2} + y^{2} = 4 \end{cases}$

Jeżeli zastosujemy metodę podstawiania, to otrzymujemy równanie z niewiadomą $x$ :

${(x - 1)}^{2} + {(- x + 4)}^{2} = 4$ .

Równanie przekształcamy do postaci $2 x^{2} - 10 x + 13 = 0$ .

Ponieważ wyróżnik tego równania jest mniejszy od $0$ , więc równanie nie ma rozwiązań, zatem układ równań nie ma rozwiązania.

Prosta i okrąg nie mają punktów wspólnych.

Słownik

równanie okręgu

postać ogólna: $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , promień okręgu $r = \sqrt{a^{2} + b^{2} - c}$ , $S = (a, b)$ - środek okręgu

postać kanoniczna: ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , $r$ - promień okręgu, $S = (a, b)$ - środek okręgu

równanie prostej

postać ogólna: $A x + B y + C = 0$ , gdzie $A$ , $B$ , $C$ oraz $A$ i $B$ nie są jednocześnie równe $0$

postać kierunkowa: $y = a x + b$ , gdzie $a$ , $b$ $\in ℝ$

Wprowadzenie

Aplet

Słownik