Przeczytaj
Nierównością wielomianową stopnia nazywamy każdą nierówność postaci:
lub lub lub ,
gdzie:
– jest wielomianem stopnia .
Aby rozwiązać nierówność wielomianowąnierówność wielomianową, najpierw postępujemy podobnie do rozwiązywania równań. Możemy rozłożyć odpowiedni wielomian na czynniki, a następnie obliczamy pierwiastki wielomianu.
Następnie, szkicując wykres wielomianu odczytujemy, dla jakich wielomian przyjmuje żądane wartości.
Rozwiążemy nierówność .
Aby rozwiązać nierówność, posłużymy się wykresem funkcji wielomianowej . Funkcja ma trzy pojedyncze miejsca zerowe , , .
Narysujemy teraz szkic wykresu funkcji wielomianowej. Dokładny wykres możemy otrzymać korzystając z programów komputerowych. Dla nas najważniejsze jest określenie, dla jakich argumentów wykres funkcji wielomianowej znajduje się poniżej osi lub na osi .
Aby wykonać szkic wykresu funkcji wielomianowej, zaznaczamy na osi X miejsca zerowe wielomianu (jeżeli istnieją). Przez te punkty na osi przechodzi wykres. Ma on kształt „wężyka” rysowanego linią ciągłą. Wykres spotykając się z pojedynczym pierwiastkiem wielomianu „przechodzi” na drugą stronę osi .
Ważne jest również jak rozpoczynamy rysowanie wykresu. Najczęściej zaczynamy rysować wykres od strony prawej do lewej.
Zaczynamy od góry, wtedy gdy współczynnik przy najwyższej potędze zmiennej jest dodatni.
W naszym przykładzie współczynnik przy najwyższej potędze zmiennej jest równy 1.
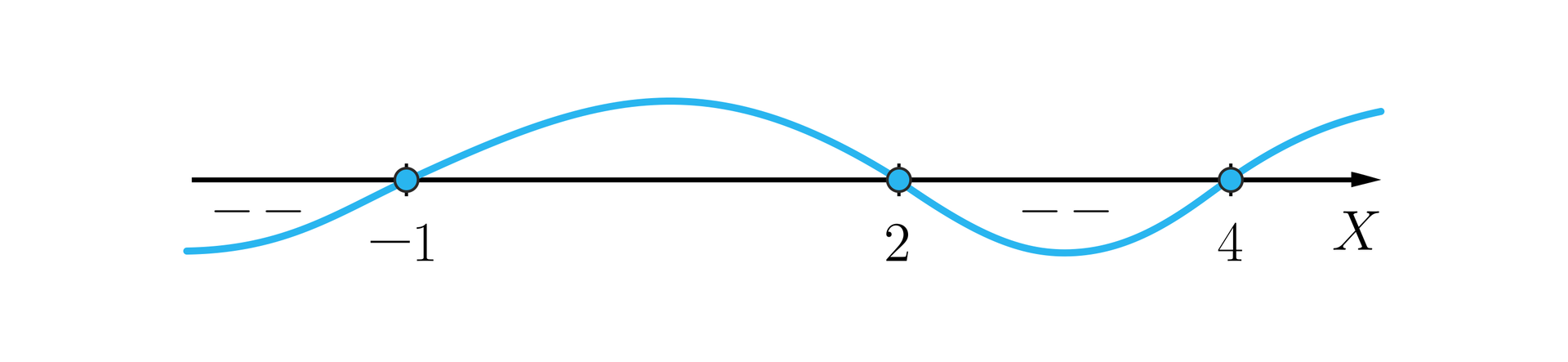
W tych przedziałach, gdzie wykres znajduje się pod osią lub na osi funkcja wielomianowa przyjmuje wartości mniejsze lub równe zero (niedodatnie).
Zbiorem rozwiązań nierówności jest .
Rozwiążemy nierówność .
Obliczymy takie x, dla których odpowiednie wyrażenie jest równe zero.
lub lub
lub (podwójny pierwiastek) lub
Sporządzimy teraz szkic wykresu funkcji wielomianowej .
W tym celu najpierw zaznaczamy na osi miejsca zerowe wielomianu. Wykres funkcji zaczniemy rysować od prawej strony i od dołu, ponieważ współczynnik przy najwyższej potędze niewiadomy jest ujemny.
Należy również zwrócić uwagę, że liczba jest podwójnym pierwiastkiem wielomianu, zatem wykres „odbija” się od osi .

Zbiorem rozwiązań nierówności jest .
Jeżeli pierwiastek wielomianu ma krotność nieparzystą, to wykres funkcji wielomianowej przechodzi na drugą stronę osi .
Jeżeli pierwiastek wielomianu ma krotność parzystą, to wykres funkcji wielomianowej „odbija” się od osi (jest do niej styczny).
Jeżeli współczynnik przy najwyższej potędze niewiadomej jest dodatni, wówczas wykres funkcji wielomianowej rysujemy od prawej strony, zaczynając od góry.
Jeżeli współczynnik przy najwyższej potędze niewiadomej jest ujemny, wówczas wykres funkcji wielomianowej rysujemy od prawej strony, zaczynając od dołu.
Rozwiążemy nierówność .
Obliczymy takie x, dla których odpowiednie wyrażenie jest równe zero.
(potrójny pierwiastek) lub (podwójny pierwiastek) lub (podwójny pierwiastek)
Wykres zaczniemy rysować od dołu.

Zbiór rozwiązań nierówności to .
Rozwiążemy nierówność .
lub lub
lub lub
lub
Czyli:
– krotny pierwiastek,
– pojedynczy pierwiastek,
– pojedynczy pierwiastek.

Zbiór rozwiązań nierówności to .
Słownik
każda nierówność postaci:
lub lub lub ,
gdzie:
– jest wielomianem stopnia