Przeczytaj
Własności prostopadłościanu i kuli są wszystkim dobrze znane. Potrafimy obliczyć objętość oraz pole powierzchni tych figur przestrzennych. W tym materiale zajmiemy się obiektem, który jest połączeniem kuli i prostopadłościanu oraz nauczymy się jak wykonać przekrój, który pomoże nam w rozwiązaniu wielu zadań.
Przyjmijmy następującą definicję:
Prostopadłościan jest wpisany w kulę, jeśli wszystkie wierzchołki prostopadłościanu leżą na powierzchni kuli.
Możemy zamiennie używać określenia: prostopadłościan jest wpisany w kulę lub kula jest opisana na prostopadłościanie.
We wszystkich przykładach i zadaniach będziemy posługiwać się odpowiednim przekrojem i oznaczeniami jak na rysunku:
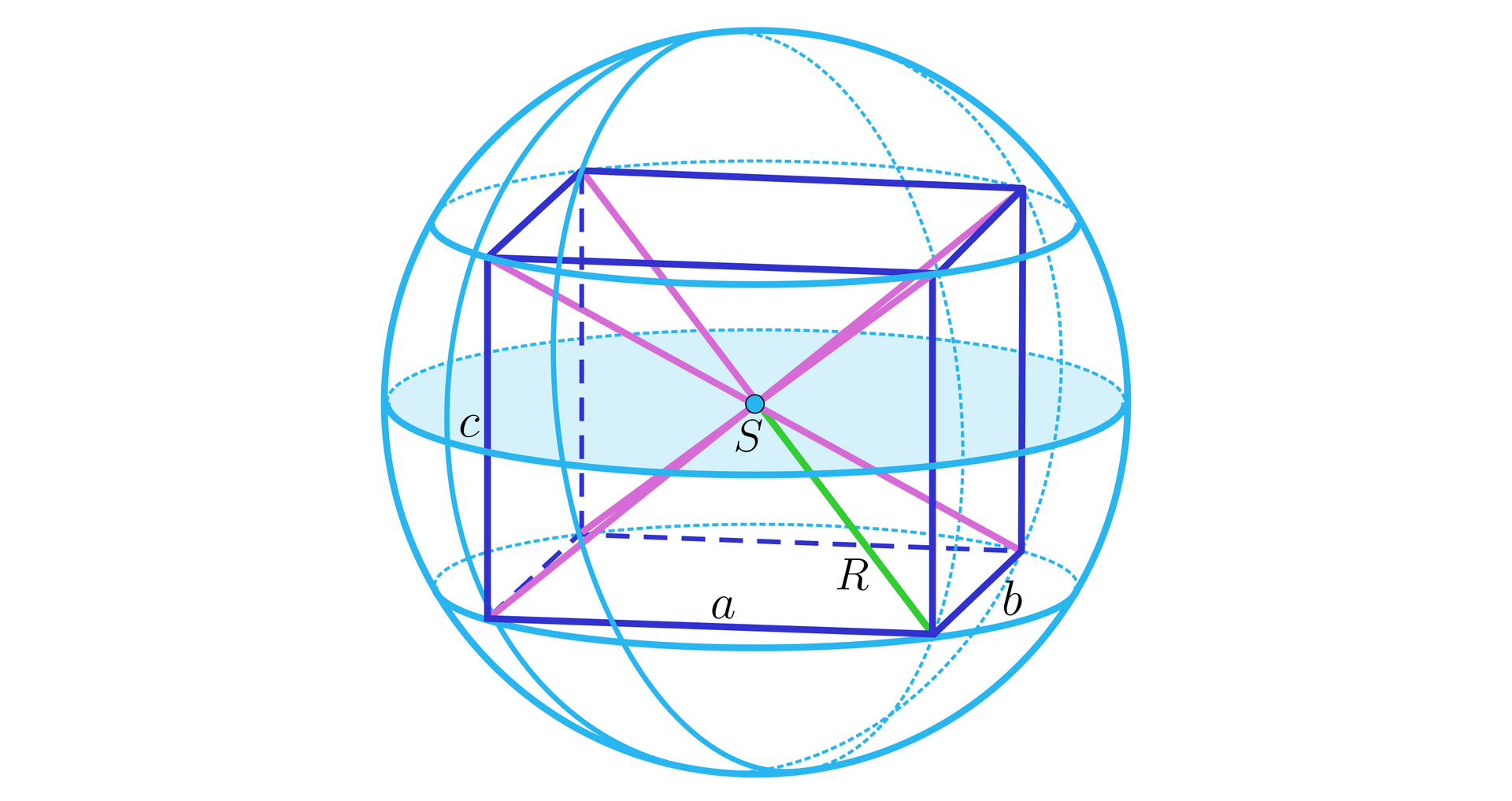
gdzie:
, , – długości krawędzi prostopadłościanu,
– promień kuli opisanej na prostopadłościanie,
– środek kuli opisanej na prostopadłościanie.
Przekrój płaszczyzną zawierającą przekątną prostopadłościanuprzekątną prostopadłościanu i przekątną podstawy.
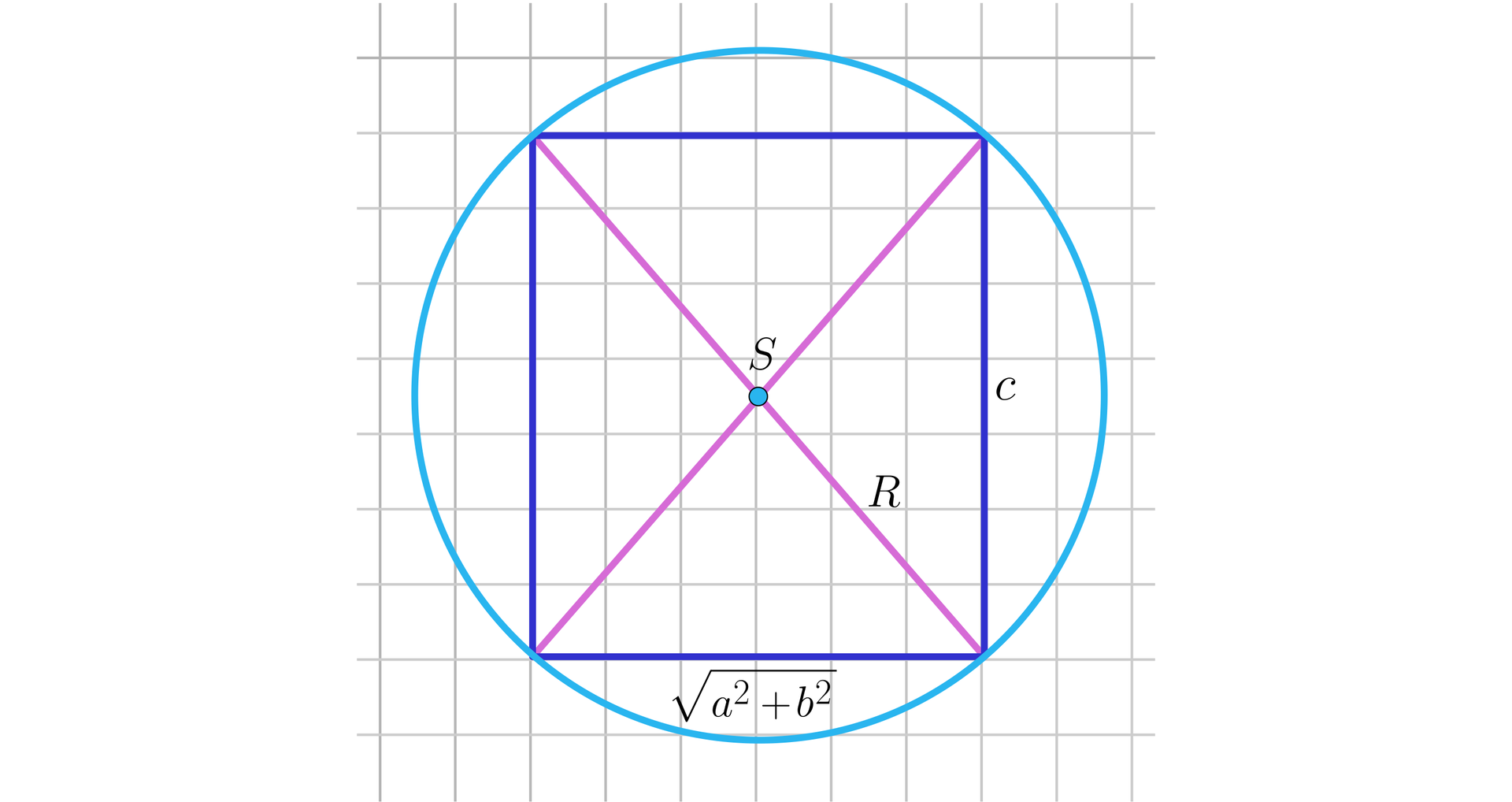
Zauważmy, że przekątna prostopadłościanu jest średnicą kuli opisanej na tym prostopadłościanie.
A zatem, korzystając z twierdzenia Pitagorasa, możemy obliczyć promień kuli w zależności od długości krawędzi prostopadłościanu.
Obliczymy objętość kuliobjętość kuli opisanej na prostopadłościanie, którego krawędzie mają długości , i .
Rozwiązanie:
.
Objętość prostopadłościanuObjętość prostopadłościanu wynosi . Jedna z krawędzi ma długość , a stosunek dwóch pozostałych krawędzi wynosi . Obliczymy pole powierzchni kuli opisanej na tym prostopadłościanie.
Rozwiązanie:
Skoro stosunek długości dwóch krawędzi prostopadłościanu wynosi to możemy przyjąć, że oraz , gdzie jest dowolną liczbą rzeczywistą dodatnią.
Wykorzystując informację o objętości prostopadłościanu otrzymujemy równanie:
A zatem , i .
Promień kuli opisanej na tym prostopadłościanie jest równy
Pole powierzchni kuliPole powierzchni kuli jest równe .
Przekątna jednej ze ścian bocznych prostopadłościanu ma długość i tworzy z płaszczyzną podstawy kąt . Przekątna sąsiedniej ściany bocznej tworzy z płaszczyzną podstawy kąt . Obliczymy średnicę kuli opisanej na tym prostopadłościanie.
Rozwiązanie:
Zauważmy, że kąt między przekątną ściany bocznej prostopadłościanu, a płaszczyzną podstawy, to kąt między przekątną ściany i krawędzią podstawy.
Wykonajmy odpowiedni rysunek.
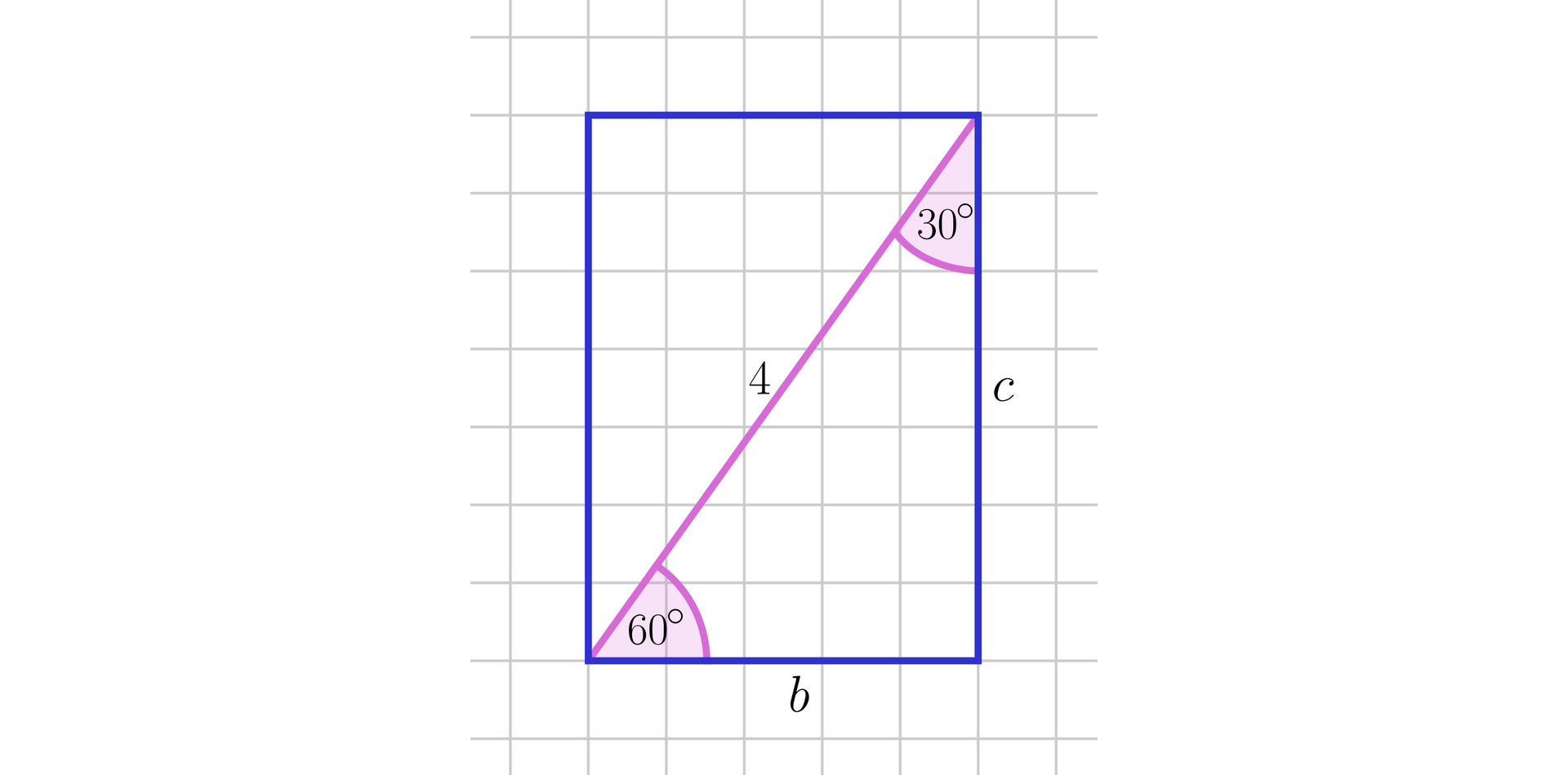
Korzystając z własności trójkąta prostokątnego o kątach , otrzymujemy oraz .
Sąsiednia ściana boczna jest kwadratem o boku długości .
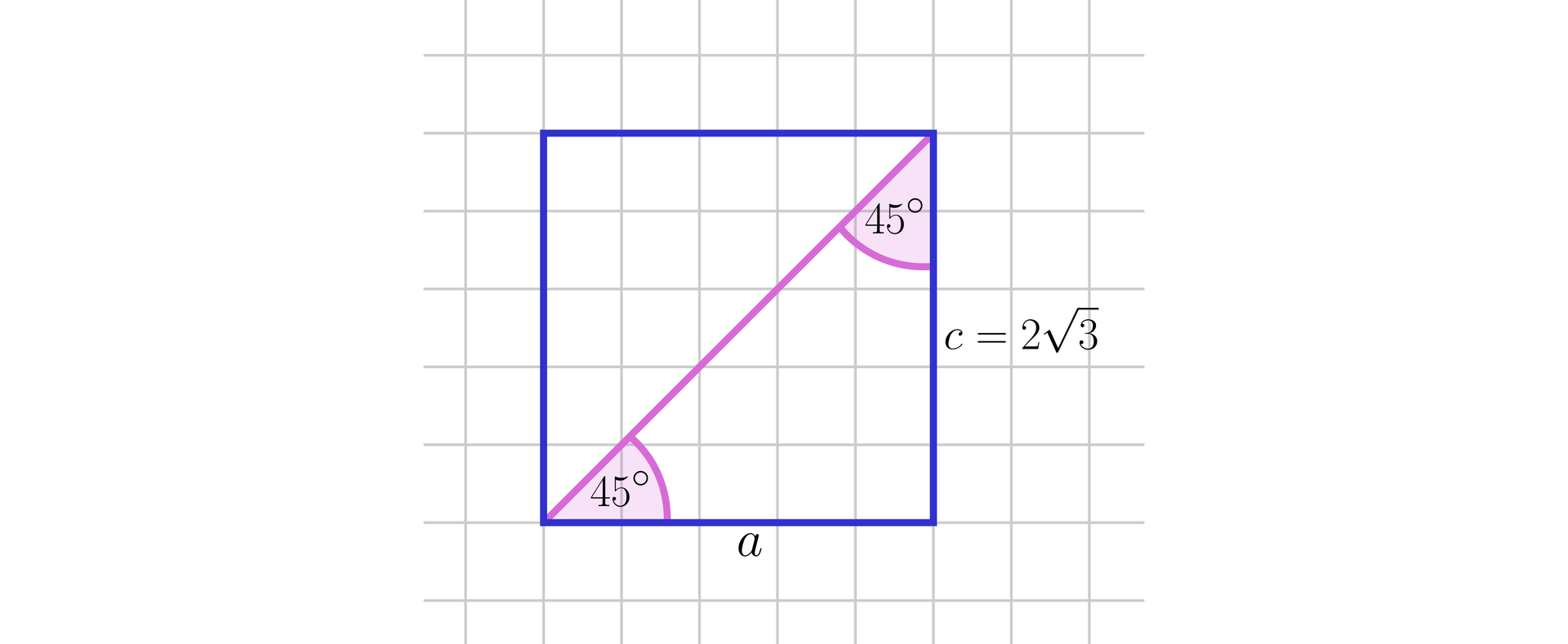
Stąd krawędź podstawy .
A zatem .
W kulę o powierzchni wpisano prostopadłościan którego podstawą jest kwadrat o przekątnej . Jaka jest wysokość tego prostopadłościanu?
Rozwiązanie:
Wyznaczymy promień kuli. Otrzymujemy równanie:
Stąd .
Do rozwiązania zadania wykorzystamy przekrój prostopadłościanu płaszczyzną zawierającą przekątną bryły i przekątną podstawy.
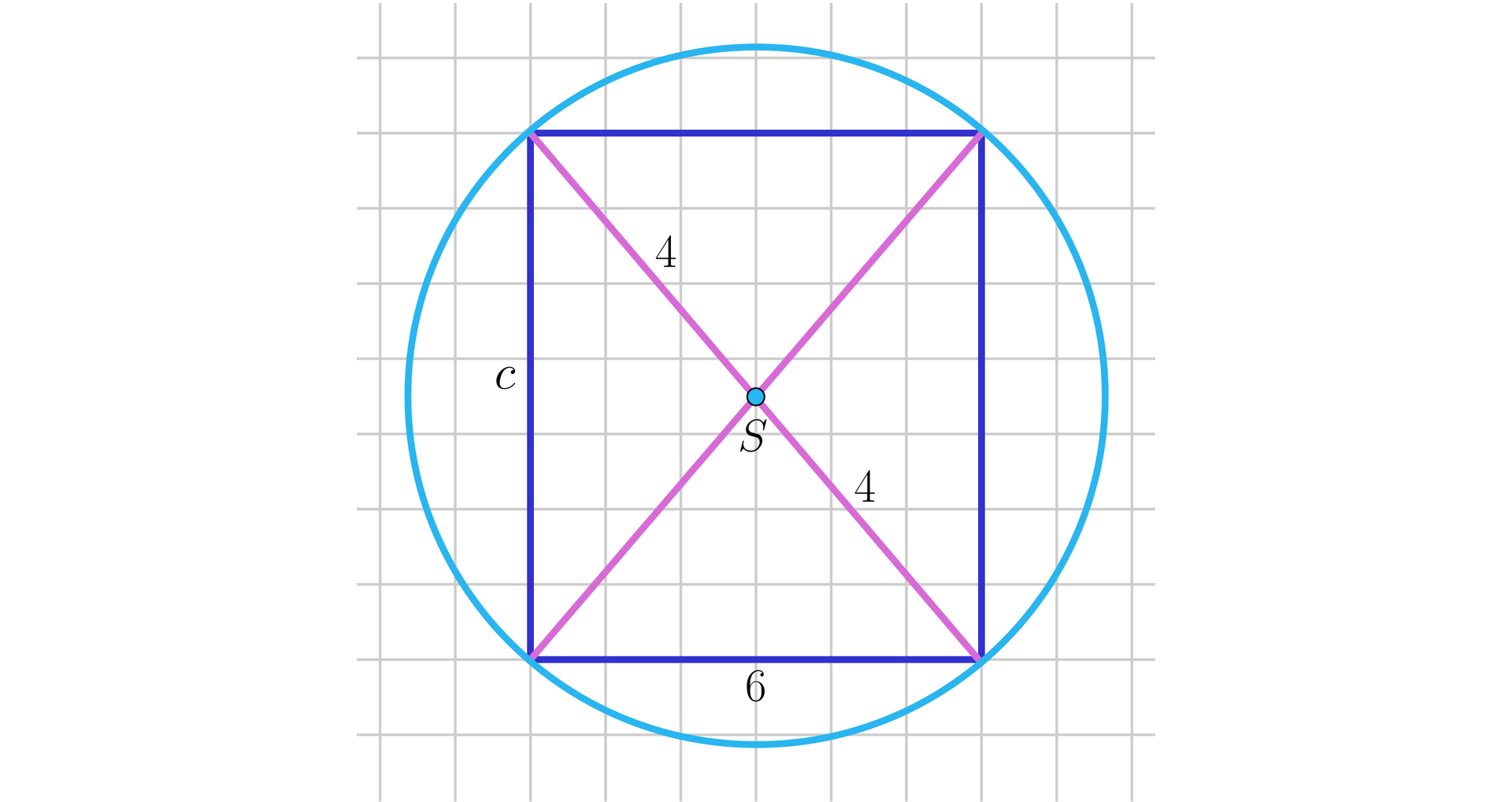
Z twierdzenia Pitagorasa otrzymujemy:
.
Obliczymy długość najmniejszego z okręgów wyznaczonych przez wierzchołki ściany graniastosłupa prawidłowego czworokątnego o polu podstawy równym i wysokości .
Rozwiązanie:
Z treści zadania wiemy, że podstawą jest kwadrat o polu , zatem jego krawędź podstawy ma długość . Wynika stąd, że pole powierzchni podstawy jest mniejsze niż pole powierzchni ściany bocznej: .
Wierzchołki prostopadłościanu leżą na sferze, wówczas możemy wyciąć poprzecznie z tej strefy okrąg wyznaczony przez wierzchołki górnej lub dolnej podstawy.
Do rozwiązania zadania wykorzystamy przekrój prostopadłościanu płaszczyzną zawierającą jego podstawę.
Zauważmy, że przekątna kwadratu jest także średnicą okręgu opisanego na tej figurze. Ze wzoru na przekątną kwadratu dostajemy, że .
Korzystając ze wzoru na długość okręgu , gdzie otrzymujemy, że .
Słownik
Objętość prostopadłościanu to iloczyn długości trzech krawędzi wychodzących z jednego wierzchołka.
Wzór na objętość prostopadłościanu o krawędziach , i :
Kula powstaje przez obrót dowolnego koła wokół jego średnicy.
Wzór na objętość kuli o promieniu :
Wzór na pole powierzchni kuli o promieniu :
Przekątna prostopadłościanu to odcinek łączący dwa najdalej oddalone od siebie wierzchołki. Wzór na przekątną prostopadłościanu o krawędziach , i :