Przeczytaj
Czworokąt (wypukły) mający przynajmniej jedną parę boków równoległych.
Parę boków równoległych nazywa się podstawami, pozostałe boki noszą nazwę ramion, odległość między podstawami nazywa się wysokością trapezu.
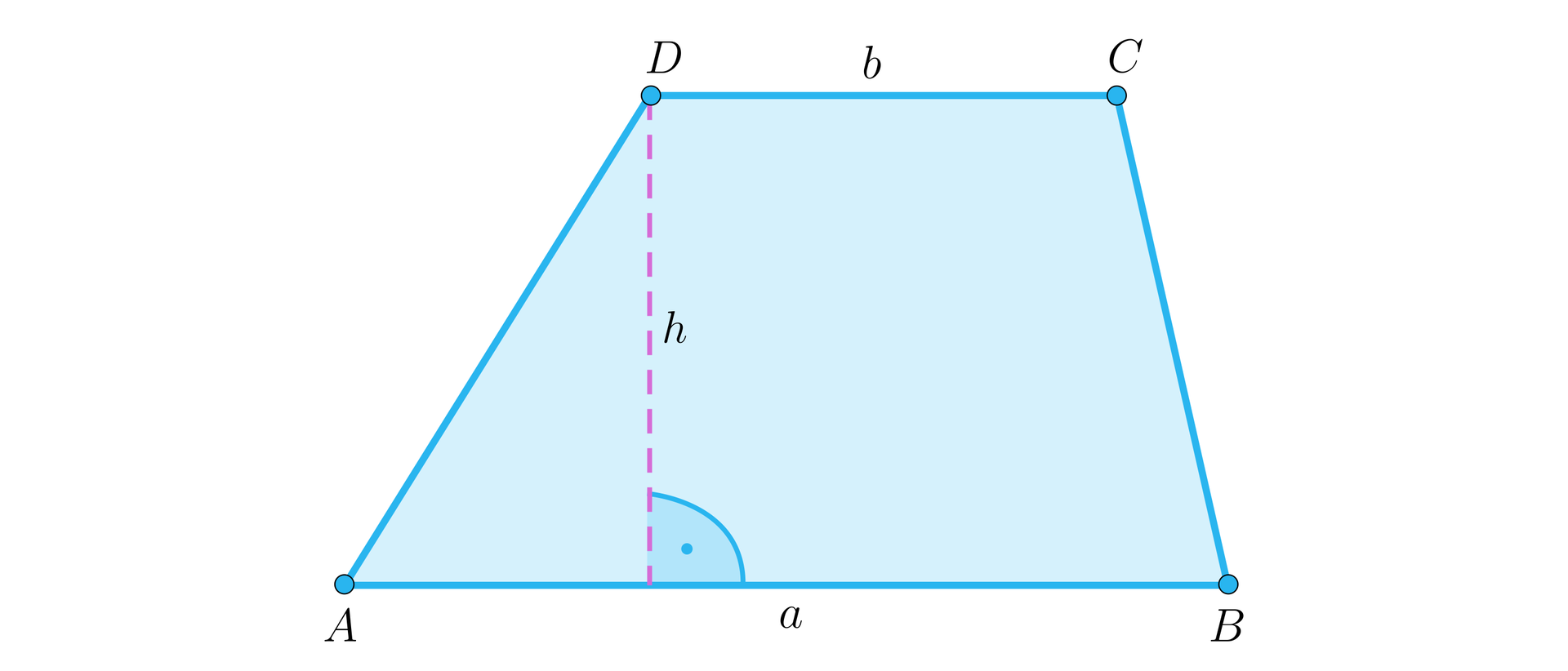
Przypadki szczególne:
trapez równoramienny: trapez o ramionach równej długości;
trapez prostokątny: trapez, którego przynajmniej dwa kąty wewnętrzne są proste.
Teraz przytoczymy kilka własności trapezu.
Z powyższej własności wynika, że dwusieczne kątów wewnętrznych przy tym samym ramieniu są prostopadłe.
Pole trapezu to iloczyn połowy sumy długości podstaw oraz jego wysokości, zatem
Załóżmy, że przekątne i czworokąta przecinają się w punkcie .
Udowodnimy, że można scharakteryzować trapez, dostrzegając równość pewnych pól powstałych trójkątów.
Niech oznacza punkt przecięcia przekątnych. Pokażemy, że czworokąt jest trapezem wtedy i tylko wtedy, gdy trójkąty i mają równe pola.

Rozwiązanie
Przeanalizujmy poniższe zdania:
jest trapezem o podstawach i ;
odległości punktów i od prostej są równe;
pola trójkątów i są równe;
sumy pól trójkątów i oraz i są równe;
pola trójkątów i są równe.
Równoważność powyższych zdań potwierdza przytoczoną wcześniej własność.
Przy okazji powyższego podziału na trójkąty warto zauważyć inną charakterystykę trapezu
trójkąty i są podobne. Wynika to wprost z twierdzenia Talesa.
Bardzo ciekawy wniosek otrzymamy po przeanalizowaniu długości pewnych odcinków równoległych do podstaw trapezu.
Na początek scharakteryzujmy, o jakie odcinki chodzi.
Przyjmijmy, że mamy dane długości podstaw trapezu , .
Niech będzie środkiem ramienia , - środkiem ramienia .

Wyznaczymy długość odcinka .
Rozwiązanie
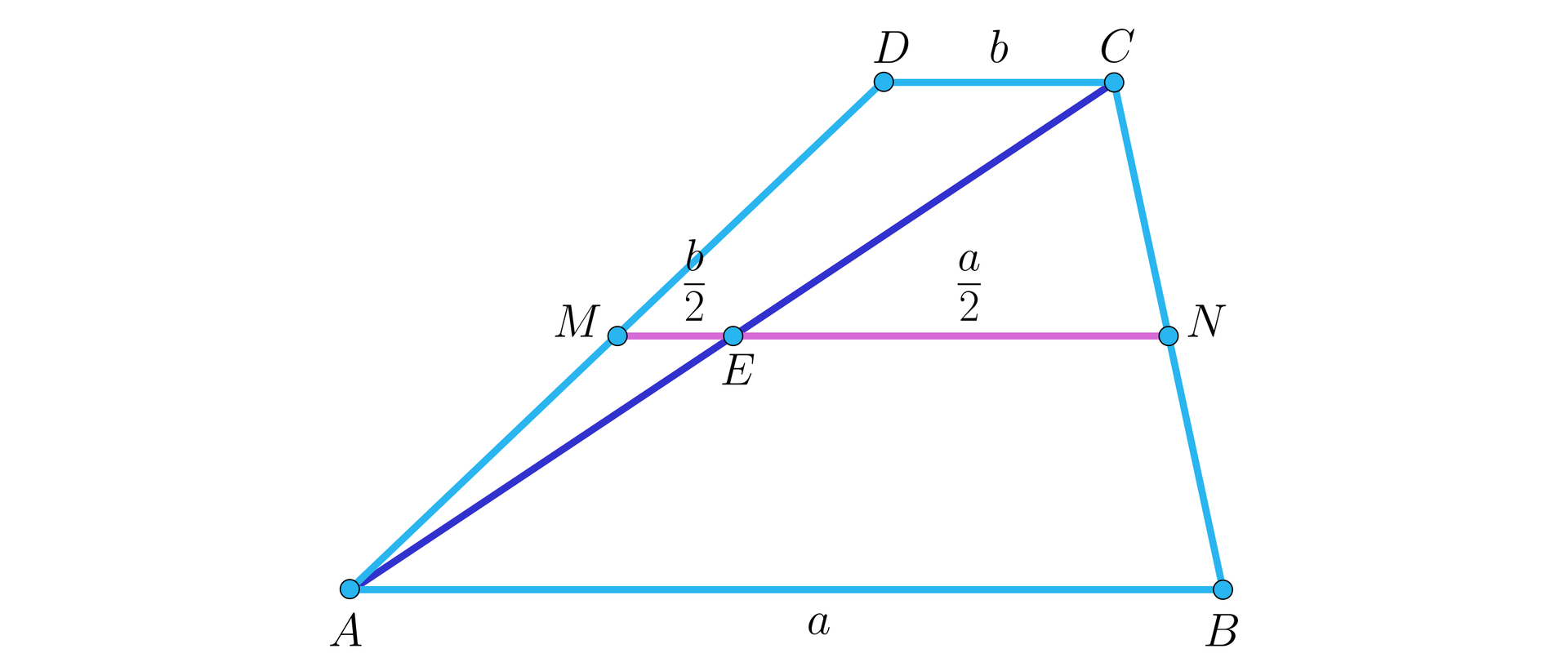
Przyjmijmy, że punkt to środek przekątnej . Wtedy, korzystając z własności linii środkowej w trójkącielinii środkowej w trójkącie, oraz .
Odcinki i są równoległe do podstaw, więc punkty , , są współliniowe.
Możemy zatem obliczyć szukaną długość odcinka
.
Wyznaczymy długość odcinka , który jest równoległy do podstaw oraz dzieli trapez na dwa trapezy podobne.
Rozwiązanie

Ponieważ trapezy i są podobne, to zachodzi zależność:
.
Szukana długość odcinka jest więc równa
.
Zastanówmy się, jaką długość ma odcinek , który jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych trapezu (rysunek).
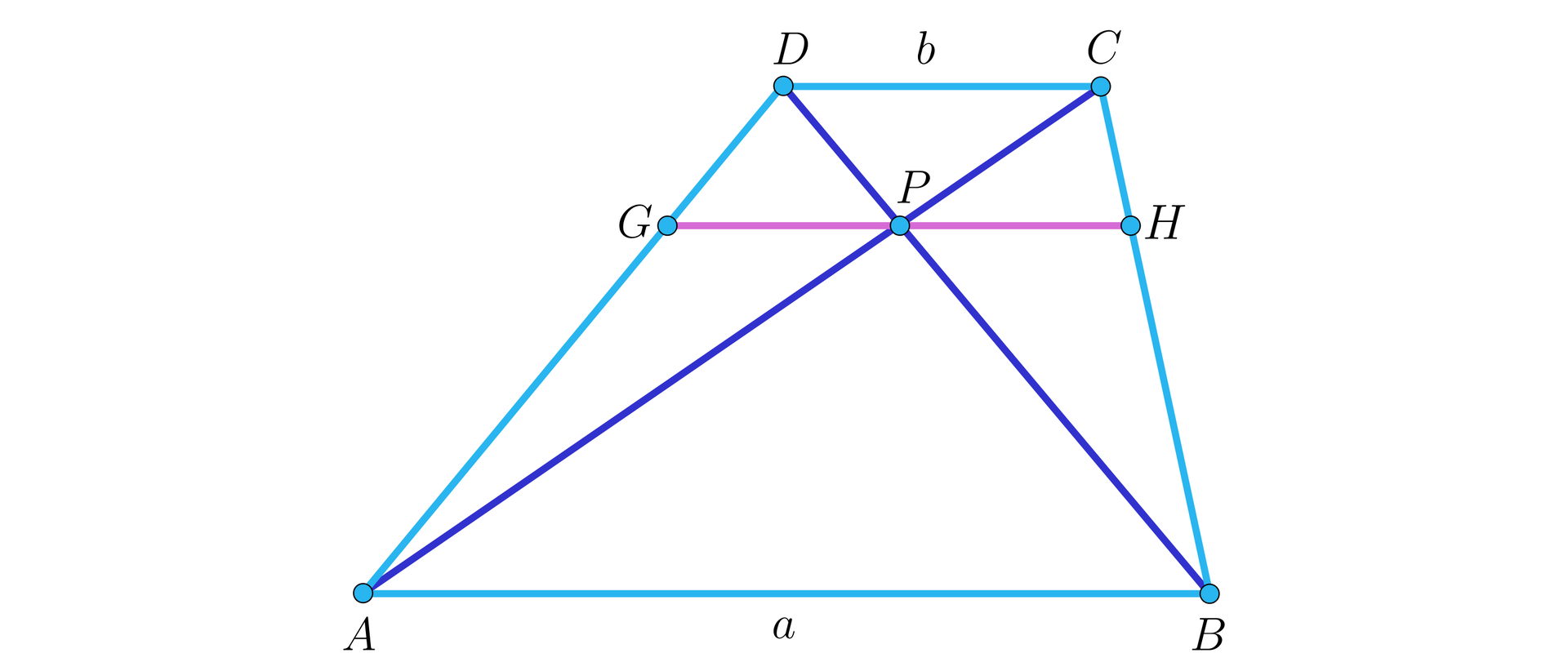
Rozwiązanie
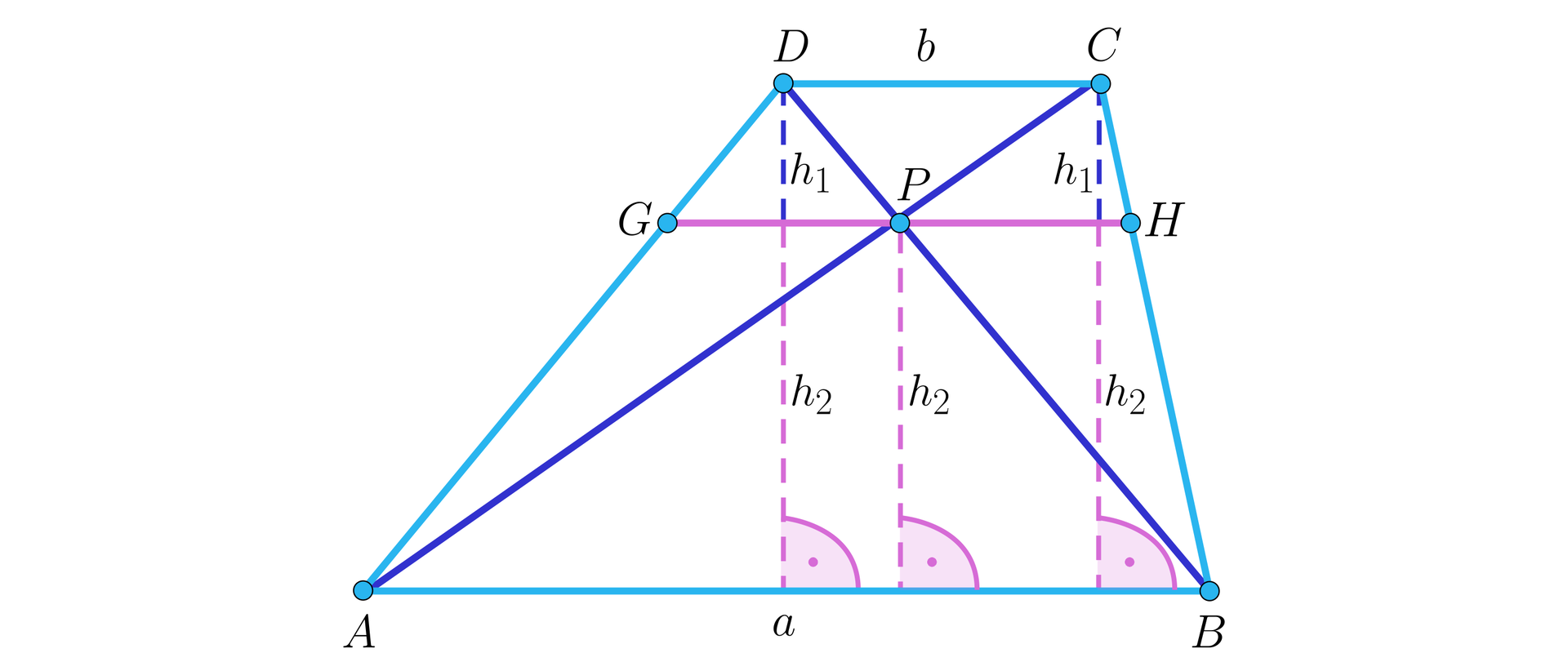
Niech będzie punktem przecięcia przekątnych trapezu.
Na początku pokażemy, że odcinki i mają równą długość.
Ponieważ trójkąty i są podobne (cecha kąt‑kąt‑kąt), to stosunki odpowiednich boków są równe stosunkom odpowiednich wysokości
.
Analogicznie, z podobieństwa trójkątów i (cecha kąt‑kąt‑kąt)
.
Ponieważ prawe strony powyższych proporcji są równe, otrzymujemy
.
Teraz przejdźmy do wyznaczenia długości odcinka .
Z powyższej obserwacji wiemy, że wystarczy obliczyć długość . Zapiszemy jeszcze raz proporcję
,
więc
.
Zauważmy, że na podstawie podobieństwa trójkątów i (cecha kąt‑kąt‑kąt), możemy wyznaczyć proporcję
.
Ostatecznie otrzymujemy
.
Na koniec obliczymy długość odcinka równoległego do podstaw trapezu, który dzieli ten trapez na dwa trapezy o równych polach.
Rozwiązanie

Przyjmijmy oraz wysokość trapezu - .
Pola trapezów i są równe, więc ich wartość to połowa pola trapezu
,
analogicznie
.
Z powyższych równań wyznaczamy oraz :
,
.
Wiemy ponadto, że .
Zatem otrzymujemy równanie
,
które po podzieleniu obustronnym przez ma postać
.
Otrzymaliśmy już równanie z jedną niewiadomą .
Po prostych przekształceniach otrzymujemy
.
Zatem długość odcinka jest równa .
Długości szukanych odcinków w trapezie okazały się być równe odpowiednim średnim podstaw. Podsumujmy więc powyższe przykłady.

Powyższy wniosek (nierówność) nazywamy nierównością między średniminierównością między średnimi lub nierównością Cauchy’ego między średnimi.
Słownik
odcinek łączący środki pewnych dwóch boków trójkąta; odcinek, który łączy środki dwóch boków trójkąta jest równoległy do trzeciego boku, a jego długość jest równa połowie tego boku.
czasem nierówności Cauchy’ego między średnimi; nierówności porządkujące w ciąg nierosnący cztery średnie tj. średnią kwadratową, arytmetyczną, geometryczną i harmoniczną wyznaczone dla tego samego układu liczb dodatnich
ich nazwa pochodzi od nazwiska Augustina Louisa Cauchy’ego, francuskiego matematyka